基于半赫兹接触的车轮磨耗预测分析

牛江 池茂儒 李大柱 罗贇

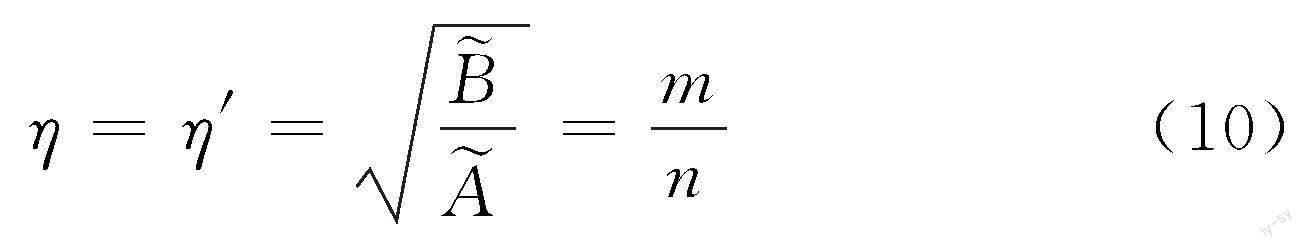
摘要：为了对比赫兹与半赫兹接触算法在轮轨磨耗仿真过程中的差异，建立CR400BF动车组动力学模型，分别基于赫兹接触与半赫兹接触算法（STRIPES）进行长距离仿真，用Archard磨耗模型计算磨耗量，以实测250 000km踏面磨耗量为参照分别比较两种算法的计算结果。结果表明：不同钢轨廓形对应磨耗量及磨耗分布差异明显；不同磨耗里程下半赫兹接触的接触斑形状差异明显，接触斑面积逐渐增大且最大接触应力逐渐减小；磨耗前期，两种接触算法得到的磨耗量及磨耗分布差异不大，且与实测结果较为接近，但磨耗中后期，两种算法得到的磨耗量较实测结果都偏大且半赫兹接触较赫兹接触更加符合实测结果，原因在于随着磨耗里程增大，轮轨接触不再满足赫兹接触假设。

关键词：轮轨接触；车轮磨耗；半赫兹接触；Archard模型

中图分类号：U270

DOI：10.3969/j.issn.1004132X.2023.07.012

Predictive Analysis of Wheel Wear Based on Semi-Hertzian Contact

NIU Jiang CHI Maoru LI Dazhu LUO Yun

State Key Laboratory of Traction Power，Southwest Jiaotong University，Chengdu，610036

Abstract： In order to compare the differences between Hertzian and semi-Hertzian contact algorithms in wheel-rail wear simulation processes， a dynamic model of CR400BF electric motor train unit（EMU） was established. Long-distance simulations were conducted based on Hertzian and semi-Hertzian contact algorithms（STRIPES）， and the wear was calculated using Archard wear model. The calculated results of the two algorithms were compared respectively with the measured tread wear of 250 000 km. Results show that the wear amount and distribution of different rail profiles are obviously different. The shapes of the semi-Hertzian contact patch are obviously different under different wear mileages， the contact patch areas increase and the maximum contact stresses decrease gradually. At early stage of wear， the abrasion and distribution obtained by the two contact algorithms have little difference and are close to the measured results. But at later period， the abrasions of two kinds of algorithm are larger than the measured results， and the semi-Hertzian contact is more in line with the measured results than that of Hertzian contact. The reason is that with the increasing abrasion mileage， wheel/rail contact no longer meets the Hertzian contact hypothesis.

Key words： wheel-rail contact； wheel wear； semi-Hertzian contact； Archard model

0 引言

隨着我国铁路线路的逐渐延伸，铁路运行工况的多元化及线路服役时间的增长，轮轨磨耗问题变得日渐突出和复杂，而踏面的微小变化将直接导致轮轨关系的改变进而影响车辆的动力学性能，而后者又会反过来影响前者，因此对车轮踏面在服役过程中的磨耗情况进行分析及预测变得尤为重要。在轮轨磨耗研究中，基于赫兹接触理论与FASTSIM算法的轮轨接触模型使用最为广泛。近年来，随着计算机技术的快速发展，国内外学者对半赫兹接触算法进行了深入研究并用于磨耗计算中。QUOST等［1］基于3个测试工况，以CONTACT方法为对照，对半赫兹接触方法进行了计算评估，这些测试用例不符合赫兹理论所要求的假设，结果表明半赫兹计算方法在非赫兹工况下快速可靠，在赫兹工况下结果精确，因此可以用于铁路车辆仿真； ENBLOM等［2］研究了半赫兹接触算法对车轮磨损率及接触斑廓形的影响，并与赫兹及CONTACT方法进行了比较，认为半赫兹接触的磨耗更加趋向于轮缘；李玉怡［3］以CONTACT算法为基准，对比了非赫兹与赫兹接触算法在不同轮轨型面接触问题上的计算精度；马晓川等［4］从轮轨静态接触几何参数和非赫兹滚动接触两方面，分析了磨耗车轮与60轨及60N轨的静态接触特性；丁军君等［5-6］基于赫兹、半赫兹及CONTACT算法分别比较了轮轨接触应力及接触斑形状，认为考虑弹性滑动速度时的半赫兹磨耗深度更接近于CONTACT计算结果，并且基于半赫兹接触理论对某货车进行了磨耗预测;姚永明等［7］研究了车轮磨耗对车辆动力学性能的影响，认为车轮磨耗严重影响车辆的平稳性及安全性，因此到达一定里程后需要对其进行璇修。

本文基于赫兹及半赫兹接触算法建立CR400BF动力学模型，以实测磨耗数据为依托，分别对磨耗模型进行修正，然后对某一实测线路进行长距离仿真，进而分析两种接触算法在磨耗过程中的差异性，为今后在磨耗预测中接触算法的选择提供一定的理论依据。

1 仿真模型的建立

1.1 车轨系统动力学模型

在多体动力学仿真软件Simpack中建立CR400BF型动车组（EMU）拖车的动力学模型，如图1所示，模型由1个车体、2个构架、4个轮对、8个轴箱组成。车体、构架、轮对各有6个自由度，各部件用刚体进行仿真，轨底坡为1∶40，轨距为1435 mm， 轨道激扰使用图2所示的实测的武广谱，不考虑牵引制动等工况。

1.2 轮轨滚动接触模型

赫兹接触算法基于弹性半空间假设［8］，两接触体在接触斑内有不变的主曲率，挤压变形前两者的间隙可以表示为

式中，A、B为接触点的相对曲率;rw、rr为接触点各主曲率半径;Rwx为轮轨接触点实际滚动圆半径;Rwy为接触点踏面横断面外形半径;Rry为接触点钢轨横断面外形半径；α为主曲率对应主方向之间夹角。

从而得到赫兹接触的长、短半轴长度分别为

式中，m、n为赫兹接触的中间参数，一般通过查表法求得;FN为接触斑法向力;μ为泊松比;E为材料的弹性模量。

赫兹接触中法向力pz为半椭球体分布：

式中，p0为接触斑最大法向应力。

从而得到相对压入量δ与法向力的关系：

式中，r为中间参数。

AYASSE等［9］基于Kik-Piotrowski计算模型（简称KP模型）中提出的虚拟渗透原理提出了一种半赫兹接触算法STRIPES［9-10］，如图3所示，两者的主要差异在于KP模型中缩放系数ε为固定值，而STRIPES中ε为计算得出，其值与曲率相关［11］。假设虚拟渗透区域的廓形满足：

式中，x-l，t（y）表示接触斑沿x轴的前沿和后端。

假设虚拟压入量为δ0时，联立式（1）和式（5）得到接触区为

半赫兹接触是通过单独修正A或同时修正A和B使得到的接触斑在计算赫兹接触时与赫兹算法相同。假设修正后的接触斑为

于是需要椭圆半轴比满足：

此时需要：

h0=εδ（11）

联立式（4）、式（9）和式（11）得到

联立式（6）、式（12）和式（13）得到

得到虚拟渗透量为

进而得到虚拟渗透量关于y轴的函数为

g（y）=h0－f（y）（16）

f（y）是接触点的轮轨间隙，满足

式中，yc為接触边界的y轴坐标。

STRIPES算法得到的法向力不再为半椭球体分布，对应公式为

式中，xl（y）为对应条带的纵轴端点坐标；n（y）、r（y）及ε（y）为对应接触斑局部的参数，物理意义同上。

同时，为了解决由于接触斑上曲率突变而造成的接触斑形状突变问题，AYASSE等［9］提出了平滑方法，即通过改变曲率B来实现：

式中，B^为改变后的曲率;Bmin、Bmax分别为B可接受的最小值与最大值。

对于切向应力的计算，使用修正后的FASTSIM算法，计算每个条带上的法向应力和切向应力，公式如下：

式中，σz，i为法向接触应力；σx，i、σy，i为切向接触应力；G为弹性剪切模量；C11，i、C22，i、C23，i为每个条带上的蠕滑系数；ξx，i、ξy，i、ξz，i为每个条带上纵向、横向及自旋蠕滑率；ai为各条带的纵向半轴长度；ni、ri、hi、εi为对应接触斑每个条带的参数，物理意义同上。

图4所示为用STRIPES模型计算得到的非赫兹接触斑及其接触应力分布，可以看出，其接触斑廓形为非椭圆形并且应力分布不再满足半椭球形分布。

以上为单个接触斑的赫兹接触及半赫兹接触应力计算过程，而在仿真运算中轮轨的多点接触现象十分普遍，主要发生在小半径曲线通过阶段及轮轨磨耗中后期，且以两点及三点接触为主。Simpack算法最多可以同时计算5个接触斑，接触搜索算法将接触剖面分割为恒定宽度的若干纵向条带，其宽度值即为钢轨及踏面的离散步长，在钢轨剖面的局部法线方向上，对每个条带进行接触搜索。此外，该算法还对轮轨接触曲率进行平滑，从而避免曲率不连续现象。

将钢轨及踏面离散步长设置为0.0002 m，纵向离散单元数量设置为30， 对于相同的计算工况，半赫兹接触算法的计算用时约为赫兹算法用时的7倍。

1.3 磨耗模型及预测流程

轮轨磨耗计算方法根据指标不同主要分为磨耗功、磨耗指数及Archard磨耗（磨耗体积）模型［12］。Archard模型在轮轨磨耗计算中应用广泛，可以得到相对准确的结果，故文中选择此方法计算磨耗。Archard磨耗模型的表达式为

式中，Vω为表面材料移除体积;L为两物体的相对滑动距离;H为两物体中较软一方的硬度;k为磨耗系数，与两物体间接触应力及滑移速度有关。

当滑移速度小于0.2 m/s或者大于0.7 m/s时，属于轻微磨损区，当滑动速度在0.2～0.7 m/s区间内时属于严重磨损区，当接触应力大于0.8H时属于灾难性磨损区，具体取值范围如图5所示。

对于接触斑内的单个接触单元的磨耗量ΔzA，可以表示为

式中，fz（x，y）为接触斑内对应位置的法向接触应力；Δd为接触斑滑动区某单元滑动距离。

接触斑滑动区单元的滑动距离可以由其合蠕滑率vslip、单元长度Δl及车轮滚动速度v得到：

式中，vslipx、vslipy分别为接触单元的纵向及横向相对滑移速度。

多点接触时需要将所有接触斑的磨耗量分别求得。磨耗系数的初始值全部取为中间值，即k2=k4=5×10-4，k3=35×10-4，k1=350×10-4。

图6所示为一个循环内对车轮磨耗的计算及踏面更新流程，计算长距离磨耗需要循环计算并对磨耗量进行累加，车轮型面的变化与车轨动力学计算是相互影响的，需要对车轮型面持续更新，文中以0.05 mm为限值对车轮型面进行更新。随着车轮踏面的不断更新，踏面廓形不断变化，在动力学计算中，将更新的踏面代入轮轨滚动接触模型中，踏面的变化将直接改变车轮滚动圆半径及轮轨接触间隙函数，进而影响曲率的计算。

由于磨耗仿真只能得到某一时刻的接触状态，进而得到系列离散值，因此得到的磨耗踏面廓形难免有突变或一阶不可导情况，从而使仿真中断或磨出凹坑，而实际踏面廓形应该是相对平滑的。因此，文中对仿真的磨耗踏面进行平滑处理：先对计算得到的磨耗量进行平滑，再对前一步磨耗踏面减去平滑后的磨耗量，最后对得到的磨耗踏面再次进行平滑处理。需要合理选取平滑相关参数，从而保证平滑后的数据与原始数据具有相同的数学特征。

2 磨耗预测模型修正

2.1 实测踏面分析

对某一线路进行了25×104 km的磨耗跟踪，踏面初始廓形为LMB_10型面，实测磨耗如图7所示。随着运行里程的增加，磨耗量逐渐增大，踏面区磨耗范围分布在-30～30 mm内，磨耗范围较小且在-20～19 mm的范围内磨耗量明显较大，这是由于轮轨接触区域主要分布在此范围内而两侧磨耗量主要由研磨子贡献［14］。

轮缘区的磨耗主要由道岔及小半径曲线造成，在前5×104 km的磨耗速率为0.057 mm/104 km， 随着里程增大，磨耗速率逐渐降低，到达25×104 km时的磨耗量为0.922 mm。由于目前的轮轨接触算法较难准确模拟列车过道岔时的轮缘接触情况，且列车在高速通过小半径曲线时轮缘区易发生塑性变形［15］，使其不再满足弹性半空间假设，同时考虑到高速列车线路条件较好，因此，在本文的研究中不考虑轮缘区磨耗。

2.2 预测模型参数分析

对预测模型的线路工况选择某实际线路，如表1所示， 可以看出，线路全程主要为直线及大半径曲线，小半径曲线占比极少。

以标准组为对照，基于单一变量原则，对影响轮轨磨耗的外界因素分别进行分析，具体工况如表2所示。CHN60及CHN60N钢轨用于比较不

同钢轨对磨耗范围及深度的影响，CHN60N钢轨由中国铁道科学研究院以CHN60钢轨为原型设计并能够适应不同车轮型面［16］，低摩擦因数工况用于模拟下雨等潮湿环境，所有工况初始踏面都为LMB_10踏面。

对以上工况分别在30 000 km的里程内计算磨耗情况，各曲线分布对照真实线路曲线占比。磨耗分布如图8所示，可以看出，相对于标准工况，使用60N钢轨得到的磨耗峰值减小了8.4%，磨耗范围也略有减小并且磨耗区域明显右移，这是60N轨的轨肩较磨耗轨更低导致的；使用60轨得到的磨耗峰值增大了4.5%且磨耗区域明显左移，这是因为60轨的轨肩较磨耗轨更高；相对于赫兹接触，半赫兹接触磨耗峰值增大了9.02%，但是磨耗范围略小，这主要是因为半赫兹接触考虑了接触斑内部的曲率变化，计算得到的接触应力峰值更大；低摩擦因数使得磨耗量略有增大，这是因为低摩擦因数使得接触斑内的滑动区占比增大进而导致磨耗量增大，但它主要影响小半径曲线，对直线及大半径曲线的影响极小。

基于实测磨耗数据对仿真磨耗进行调节，钢轨使用实测磨耗轨，同时不考虑低摩擦因数对磨耗的影响。由于实测踏面在前5×104 km的磨耗速率为0.057 mm/104 km，则3×104 km的磨耗量为0.171 mm。对于赫兹接触及半赫兹接触，仿真3×104 km的磨耗量分别为0.176 mm和0.188 mm，因此对两者的磨耗系数分别乘以0.972和0.910的修正值。

3 仿真结果分析

3.1 接触斑形状对比

图9对横移量为0时的实测初始踏面及25×104 km磨耗踏面接触斑形状进行对比分析，由于初始踏面与轨道接触较为符合赫兹接触假设，初始踏面的接触斑形状大致为椭圆形，而磨耗25×104km以后，轮轨接触间隙函数变得极其复杂，踏面与轨道已经不符合赫兹接触假设，故其接触斑形状已偏离椭圆形。

根据1.2节可知，赫兹接触计算得到的不同磨耗踏面横移量为0时接触斑始终为椭圆形。

3.2 接触面积及最大接触应力对比

在轮轨法向力相同的情况下，接触斑面积越小，接触应力越大，两者共同影响踏面磨耗的发展。分别使用赫兹及半赫兹接触算法在直线段对不同磨耗里程的仿真踏面进行分析。

图10所示为接触斑面积随磨耗里程的变化趋势，磨耗前期两者的差异并不大，半赫茲接触较赫兹接触的接触斑稍小，而随着磨耗里程增大，两者的差距也逐渐增大。对于赫兹接触，接触斑面积并没有明显的变化趋势，始终保持在80.0～95.0 mm2之间，而对于半赫兹接触，接触斑面积从69.1 mm2逐渐降低到50.3 mm2。图11所示为接触斑内最大接触应力随磨耗里程的变化趋势，赫兹接触的最大接触应力始终保持在1.3～1.5 GPa之间，而对于半赫兹接触，最大接触应力从1.67 GPa逐渐增大到2.40 GPa。

原因在于随着磨耗里程增大，踏面磨耗量持续增长，使得轮轨接触区域的相对曲率持续增大，从而直接导致实际的车轮踏面接触斑面积减小。赫兹接触由于自身的假设前提过于理想，只考虑了轮轨接触参考点的相对曲率变化，导致其接触斑内部曲率恒定，因此接触斑面积及最大接触应力变化较小；而半赫兹接触考虑了整个轮轨接触区域的接触间隙，其相对曲率A（y）和B（y）是y轴的函数，故而接触斑面积及最大接触应力对相对曲率的变化更加敏感。

3.3 实测结果与仿真结果对比

图12及图13所示为两种接触算法对应25×104 km的踏面磨耗情况及磨耗量分布，两种接触算法的磨耗范围都分布于-20～20 mm之间，与实测范围比较吻合， 随着磨耗里程增大，磨耗深度增长速率持续降低。对于赫兹接触，最大磨耗深度位置始终在-4.4 mm处，对于半赫兹接触，在10×104 km时最大磨耗深度位置在-1.6 mm处，然后随着里程增长逐渐向轮缘方向移动，在25×104 km时移动到-4.4 mm处。

将两种接触算法对应的磨耗仿真结果与实测数据进行比较，如图14所示，在5×104 km时的赫兹及半赫兹接触对应踏面磨耗量与实测结果近似，但是，随着里程增长，仿真的磨耗深度逐渐大于实测磨耗深度，在15×104km时，赫兹接触得到的磨耗深度为0.732 mm，半赫兹接触为0.71 mm。在25×104km时，赫兹接触得到磨耗深度达到1.07 mm，相对于实测值误差为16.05%，半赫兹接触为1.01 mm，误差为9.54%。可以得出，前期的仿真结果与实测结果拟合较好，但随着磨耗里程的持續增大，两种算法得到的仿真结果越来越偏离实测值，并且赫兹接触的仿真结果与实测结果差异更大。

4 结论

本文基于赫兹及半赫兹接触算法分别进行了25×104 km的磨耗仿真，分析了仿真过程中接触斑形状、接触应力及踏面磨耗量的变化趋势，并与实测数据进行了对比，得到如下结论：

（1）踏面廓形的改变将直接影响轮轨接触间隙及曲率的变化，进而影响接触斑形状、面积及接触应力，相对于赫兹接触，半赫兹接触对接触间隙及曲率的变化更加敏感。

（2）随着磨耗里程的增大，两种算法都高估了踏面磨耗量，而半赫兹接触的仿真结果与实测值拟合更好。

（3）由于半赫兹接触的计算耗时约为赫兹接触的7倍，为了提高计算效率，可以考虑在以后的磨耗仿真中前10×104 km选择赫兹接触，随后选择半赫兹接触。

参考文献：

［1］ QUOST X， SEBES M， EDDHAHAK A， et al. Assessment of a Semi-Hertzian Method for Determination of Wheel-rail Contact Patch［J］. Vehicle System Dynamics， 2007， 44：789-814.

［2］ ENBLOM R， BERG M.Impact of Non-elliptic Contact Modelling in Wheel Wear Simulation［J］.Wear， 2008， 265：1532-1541.

［3］ 李玉怡.高速列车车轮磨耗预测研究［D］. 北京：北京交通大学， 2020.

LI Yuyi. The Research on Wheel Wear Prediction of High-speed Train［D］. Beijing：Beijing Jiaotong University， 2020.

［4］ 马晓川， 王平， 王健， 等．高速铁路磨耗车轮与60N钢轨静态接触分析［J］．西南交通大学学报， 2018， 53（4）：741-747．

MA Xiaochuan， WANG Ping， WANG Jian， et al. Static Contact Analysis of Worn-wheel Profiles and 60N Rail of High-speed Railway［J］.Journal of Southwest Jiaotong University， 2018， 53（4）：741-747.

［5］ 丁军君， 李芾，黄运华. 基于半赫兹接触的车轮磨耗计算［J］. 西南交通大学学报， 2011， 46（2）：195-199.

DING Junjun， LI Fu， HUANG Yunhua. Calculation of Wheel Wear Based on Semi-Hertzian Contact［J］. Journal of Southwest Jiaotong University， 2011， 46（2）：195-199.

［6］ DING J， LI F， HUANG Y， et al. Application of the Semi-Hertzian Method to the Prediction of Wheel Wear in Heavy Haul Freight Car［J］. Wear， 2014， 314：104-110.

［7］ 姚永明， 李国芳， 丁旺才.基于Archard模型的车轮磨耗对车辆动力学性能的影响［J］.中国机械工程，2017，28（19）：2311-2317.

YAO Yongming， LI Guofang， DING Wangcai. Influences of Wheel Wear on Dynamics Performance of Vehicles Based on Archard Model［J］. China Mechanical Engineering， 2017，28（19）：2311-2317.

［8］ JOHNSON K L. Contact Mechanics［M］. Cambridge：Cambridge University Press， 1985.

［9］ AYASSE J B， CHOLLET H. Determination of the Wheel Rail Contact Patch in Semi-Hertzian Conditions［J］. Vehicle System Dynamics， 2005， 43（3）：161-172.

［10］ 孙宇. 轮轨非Hertz接触方法及其在高速铁路轮轨动力相互作用中的应用研究［D］.成都：西南交通大学，2018.

SUN Yu. Wheel-rail Non-Hertzian Contact Method and Its Application in the Study of Wheel-rail Dynamic Interaction on High-speed Railway［D］. Chengdu：Southwest Jiaotong University， 2018.

［11］ 周佳儀. 几种非赫兹轮轨滚动接触模型的对比研究［D］. 成都：西南交通大学，2021.

ZHOU Jiayi. Comparative Study of Non-Hertzian Wheel-rail Rolling Contact Models［D］. Chengdu：Southwest Jiaotong University， 2021.

［12］ LEWIS R， OLOFSSON U. Mapping Rail Wear Regimes and Transitions［J］. Wear， 2004， 257（7/8）：721-729.

［13］ ARCHARD J. Contact and Rubbing of Flat Surface［J］. Journal of Applied Physics， 1953， 24（8）：918-988.

［14］ 赵长雨， 赵鑫， 许世杰，等.城际动车组车轮廓形演化特点和原因分析［J］.铁道科学与工程学报， 2021， 18（9）：2427-2435.

ZHAO Changyu， ZHAO Xin， XU Shijie， et al. Analysis of Characteristics and Mechanisms of Wheel Profile Evolution on Intercity EMUs［J］. Journal of Railway Science and Engineering，2021， 18（9）：2427-2435.

［15］ 李国栋，曾京，池茂儒，等.高速列车轮轨匹配关系改进研究［J］.机械工程学报，2018，54（4）：93-100.

LI Guodong， ZENG Jing， CHI Maoru， et al. Study on the Improvement of Wheel-rail Matching Relationship for High Speed Train［J］. Journal of Mechanical Engineering，2018，54（4）：93-100.

［16］ 周清跃，张银花，田常海，等．60N钢轨的廓型设计及试验研究［J］．中国铁道科学，2014，35（2）：128-135．

ZHOU Qingyue， ZHANG Yinhua， TIAN Changhai. et al. Profile Design and Test Study of 60N Rail［J］. China Railway Science， 2014，35（2）：128-135.