进给系统角接触球轴承的热力耦合分析

李朕均 赵春雨

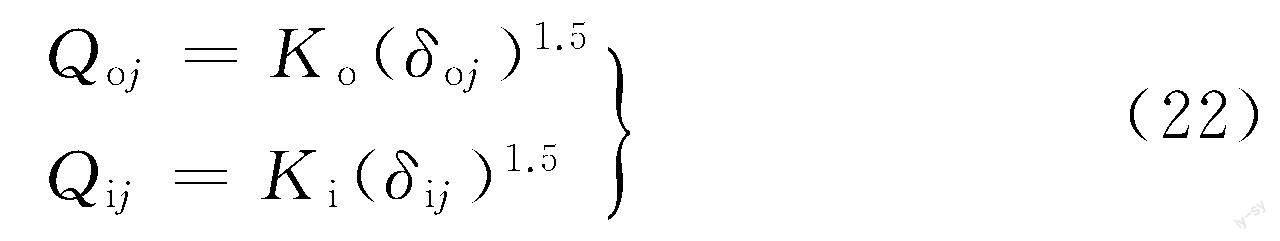
摘要：对角接触球轴承热力耦合性能进行预测分析是保证机床工作精度的关键。基于赫兹接触理论结合热网络方法，建立滚珠丝杠进给系统成对安装轴承工作状态下的动态热力耦合模型，考虑了温升热效应下的球轴承内部润滑状态以及热膨胀，提出了轴承的动态热力耦合分析数值计算方法。探明了轴承内部接触参数和摩擦生热的时变规律。研究表明：转速、外部载荷等工况影响轴承的摩擦接触特性，轴承性能显著受热力学行为的影响。提出的轴承动态热力耦合分析模型可以有效预测轴承非线性热行为下的接触特性。

关键词：数控机床进给系统；角接触球轴承；热力耦合分析；热网络法；时变动态特性

中图分类号：TH133.3

DOI：10.3969/j.issn.1004132X.2023.07.008

Thermal Mechanics Coupling Analysis of Angular Contact Ball Bearings

Installed in Pairs in Feed System

LI Zhenjun1 ZHAO Chunyu2

1.School of Mechanical Engineering， Shenyang University of Technology，Shenyang，110870

2.School of Mechanical Engineering and Automation，Northeastern University，Shenyang，110819

Abstract： The prediction and analysis of thermal mechanics coupling performance of angular contact ball bearings was the key to ensure the working accuracy of machine tools. Based on Hertz contact theory and thermal network method， a dynamic thermal mechanics coupling model of ball screw feed system pair-installed bearings was established under working conditions， the internal lubrication state and the thermal expansion of ball bearings were considered under temperature rise effect， and a numerical calculation method was proposed for dynamic thermal mechanics coupling analysis of bearings. The time-varying laws of internal contact parameters and friction heat generation of the bearings were proved. Results show that the rotational speed and the external load affect the frictional contact characteristics of bearings， and the performance of bearings is significantly affected by the thermodynamics behavior. The dynamic thermal mechanics coupling analysis model proposed herein may effectively predict the contact characteristics of bearings under nonlinear thermal behavior.

Key words： CNC machine tool feed system; angular contact ball bearing; thermal mechanics coupling analysis; thermal network method; time varying dynamic characteristic

0 引言

數控机床进给系统作为精密传动和定位的关键部件，对机床定位精度起着至关重要的作用，减少了非切削操作时间和刀具更换时间，使加工过程更加便捷。滚动轴承作为机床旋转部件中的重要支撑件，其性能好坏直接影响机床的动态特性和热特性，所以对丝杠轴承进行热分析在研究机床进给系统热误差中具有重要意义。热效应影响下，许多关键参数发生变化，如预紧力、润滑剂黏度、负荷分布和材料热膨胀等，因此在工作状态下对轴承在旋转时的热动态特性进行预测建模也变得愈加复杂和困难［1-3］。因为固有的几何和动态复杂性，轴承在热能影响下的分析并没有得到彻底解决。

角接触球轴承由于结构简单、转速高、摩擦力矩小、工作精度高等优点，广泛用作机床的支承部件［4-5］。进给轴轴承的机械特性和热特性是相互联系的，因此在实际工况下精确的热动态性能预测分析显得至关重要。国内外学者针对球轴承开展了大量研究工作。JONES［6］基于赫兹接触理论提出了高速轴承的分析模型，该模型考虑了轴承系统中各滚动元件的离心力和陀螺载荷，计算方法同时定义了系统中轴承各滚动元件的载荷。HERNOT等［7］提出了改进的角接触球轴承发热功率计算模型，该模型考虑了旋转力矩、陀螺力矩的影响，可以有效预测高温下的瞬态热行为。HARRIS［8］在JONES［6］原有模型的基础上，建立高速球轴承的准静态平衡方程，不仅考虑了惯性力的影响还包括高速状态和赫兹接触变形，通过计算轴承摩擦力矩得到轴承产生的热量。吴飞科等［9］通过实例分析求解，指出了赫兹接触理论的适用范围，为轴承的接触力学仿真计算奠定了基础。ZHAO等［10］分析了角接触球轴承工作状态对内部载荷分布、接触角以及发热功率的影响，确定了陀螺力矩、轴向力和转速平衡所需摩擦因数的变化规律。TAN等 ［11］提出了一种将准静态模型与有限元结合的方法，研究了高速主轴轴承在预载荷作用下的非线性热行为。上述大量研究工作对确定滚动轴承的热分析是帮助巨大的，但是并没有详尽地考虑热效应对角接触球轴承时变动态接触特性的影响。

本文通过对高速球轴承发热机理的分析，基于赫兹接触理论，建立了滚珠丝杠进给系统成对安装的角接触球轴承在工况下的热力耦合模型，考虑了轴承内部温升对材料的热变形和润滑油黏度的影响，通过数值计算探明了轴承热特性及接触特性的时变规律。

1 轴承拟动态接触理论模型

1.1 轴承的拟动态接触参数求解

角接触球轴承内部在实际工况下的机械性能和传热过程相互依赖且不可分割，轴承温度取决于外部载荷、转速、润滑剂特性、轴承及其周围环境的布置等因素。在建立轴承动态接触模型之前，需要确定轴承实际工作状态下的接触参数，因为内部载荷受力和内部温度状态变化会导致轴承内部一些接触参数变化，如图1所示。图中，角接触球轴承由于过盈配合和轴承内部温升引起的轴承接触角变化为

式中，A为内外沟道曲率中心之间的距离；Pd为轴承的径向游隙；α0为初始接触角；α′0为发生变化后的初始接触角；Δpf为过盈配合引起的径向间隙变化；Δpt为摩擦热引起的径向间隙变化。

HARRIS［8］针对安装在轴上的轴承给出了由于轴承过盈配合引起的轴承内外圈变化的计算公式，考虑到轴承装配后的间隙变化计算式为

Δpf=Δs+Δh（3）

式中，Δs为由于轴承过盈配合引起的轴承内圈直径增大量；Δh为由于轴承外圈与轴承座之间的配合而引起的轴承外圈直径变化量。

轴承温升热膨胀引起滚珠及内外圈发生热位移，整个热载荷引起的径向间隙变化计算式如下：

式中，Δr1为轴承内外圈热膨胀差值；Δr2为轴承滚珠的热膨胀值；Doi为轴承内圈的外径；Dio为轴承外圈的内径；αs、αb分别为轴承套圈和滚珠的热膨胀系数；ΔTi、ΔTo分别为轴承内外圈温升；ΔTb为滚珠温升;Db为滚珠直径。

由图1可知，由于过盈配合和轴承内部温升，沟槽曲率半径中心之间的距离变为A1，轴承接触角由α0增加到α′0。在预紧力作用下接触角再次增大到α′0p，而内圈滚道曲率中心Ci在轴向预紧载荷作用下移动到Ci1，预紧力Fa引起的初始接触变形轴向位移定义为δp，预紧载荷加载后的接触角为

式中，z为滚珠数量；KN为球滚道接触载荷位移刚度系数。

施加预紧力后，滚道曲率中心之间的距离Ap可定义为

由图1可以看出，在预紧力作用下，预紧导致的轴向位移δp与初始接触变形δn有关：

1.2 轴承的拟动态接触模型

轴承在高速运行时，滚动体的动力载荷（即离心力和陀螺力矩等附加载荷）将改变作用在滚珠与滚道接触区的载荷分布，载荷变化对轴承动力学特性影响显著。如图2a所示，假设外圈固定，通过施加初始轴向载荷消除滚珠轴承的内间隙，当径向载荷和力矩载荷同时作用时，角位移如图2b所示；由图2c可知，每个滚珠的负载不相等。为了求解轴承载荷作用下的参数，需要建立轴承滚珠平衡方程。

如图3所示，当轴承高速运转时，在陀螺力矩和离心力作用下，滚珠中心、轴承内圈曲率中心、轴承外圈曲率中心不再共线。滚珠与滚道曲率中心的关系可表示为

（L1j－X1j）2+（L2j－X2j）2－［（fi－0.5）Db+δij－Δr2］2=0（12）

X21j+X22j－［（fo－0.5）Db+δoj－Δr2］2=0（13）

L1j=APsin α′0p+da+βcos φj（14）

L2j=APsin α′0p+drcos φj－Δr1（15）

式中，fi為内圈沟道曲率半径系数；fo为外圈沟道曲率半径系数；为内圈沟道曲率半径；β为相对角位移；L1j、L2j分别为内外圈曲率中心之间的轴向距离和径向距离；φj为任意滚珠角位置；da为轴向位移；dr为径向位移。

为求解每个滚珠的四个未知量X1j、X2j、δij和δoj，根据图4，建立水平和垂直方向的力平衡方程：

Qijsin αij－Qojsin αoj－Pijcos αij+Pojcos αoj=0（16）

式中，Qij、Qoj分别为内外圈接触力；Pij=λijMij/Db，Poj=λojMoj/Db，这里修正系数λij=0，λoj=2，Mij、Moj分别为滚珠受到内外圈的陀螺力矩；Fcj为离心力;αij、αoj分别为滚珠与内外圈的接触角；δij、δoj分别为内外滚道的接触变形。

Qij和Qoj与法向接触变形的关系如下：

式中，Ki、Ko分别为内外圈的接触刚度。

任一滚珠位置的离心力Fcj为

式中，m为滚珠的质量；dm为轴承节圆直径；ωm为滚珠的公转角速度；ω为内圈沟道角速度。

X1j、X2j、δij和δoj在每个滚珠的角度位置通过Newton-Raphson方法求解式（18）～式（21）非线性系统方程来获得。四个未知数的值计算出来后，它们用于通过力平衡方程修正da、dr和θ：

式中，Me为力矩载荷。

1.3 轴承发热功率计算模型

摩擦热由滚珠与滚道接触区差速滑动、润滑剂黏度和滚珠与滚道接触区旋转摩擦三个部分组成，分别记为HB1、HB2和HB3，即轴承总发热功率为

H=HB1+HB2+HB3（27）

（1）滚珠与滚道接触区差速滑动摩擦发热功率。滚珠和滚道之间接触区域上的接触椭圆长轴和短轴方向发热功率Hnxj和Hnyj计算如下：

式中，J为由N·m/s到W的转换常数；n为i，o，j=1，2，…，z；τnxj、τnyj分别为椭圆长短轴方向的表面摩擦切应力；vnxj、vnyj分别为椭圆长短轴方向的滑动速度;anj、bnj分别为接触区域椭圆的长短轴。

计算每个滚珠接触区域局部热量然后累计叠加，整个轴承的发热功率HB1为

式中，H（1）B1为滚珠与内圈滚道差速滑动摩擦发热功率； H（2）B1为滚珠与外圈滚道差速滑动摩擦发热功率。

（2）润滑剂黏性引起的摩擦发热功率。润滑剂黏性摩擦力矩MB2为

式中，f0为与轴承类型和润滑方式有关的系数；n0为转速；ν0为润滑脂动力黏度。

轴承工作过程中润滑黏度产生的热量为

HB2=1.047×10－4n0MB2（32）

（3）滚珠旋转摩擦的发热功率。滚珠与滚道之间接触面上的旋转摩擦力矩为

式中，μsi、μso分别为内外圈自旋摩擦因数；a^为赫兹接触椭圆的长半轴；ζ为第二类椭圆积分。

轴承旋转摩擦产生的总热量

式中，ωsij、ωsoj分别为内圈和外圈接触区滚珠的自旋角速度；H（1）B3、H（2）B3分别为内圈和外圈接触区域自旋摩擦热。

根据BURTON等［12］的研究，滚珠与滚道产生的摩擦热平均分配到滚珠和轴承内圈中。轴承各个部分的摩擦热分别为

式中，Hi为滚珠与内圈滚道之间的摩擦发热功率；Ho为滚珠与外圈滚道之间的摩擦发热功率；Hball为轴承滚珠的摩擦发热功率。

2 轴承热力耦合数值计算方法

轴承热力耦合数值计算包括轴承温度场计算和轴承拟动态接触力学计算。温度场计算采用热网络法。针对轴承系统的对称原则，以1/4为研究对象。依据轴承单元结构，本文选择5个典型的温度节点建立了轴承的热网络模型，节点分布如图5所示。热网络模型节点间相互接触产生热传递，将节点中间阻碍热量交换的阻力设置为热阻。不同节点的接触热阻如下计算。

（1）针对安装在进给圆柱体上的轴承内外圈、轴承座等机械结构，其热阻计算如下式：

式中，di、do分别为内外径；kI为热导率；L为特征长度。

（2）滚珠和与其接触的内外滚道之间的接触热阻计算为

（3）轴与轴承孔的装配关系为过盈配合，内圈与轴的接触热阻为

式中，kd1、kd2分别为轴与轴承的热导率；AB为表观接触面积；A*R为两个接触面之间的真实接触面积；hc为轴与轴承孔的传热系数。

（4）通常热对流阻值由以下公式求解：

R=1/（ABhv）（41）

式中，hv为对流传热系数。

设图5网络对应各节点的温度为T1，T2…，T5，环境温度为T0，依据阻容传热理论，可得微分方程：

式中，Rair1为轴承座和环境的热阻；R12为轴承座和外圈的热阻；R23为滚珠和外圈的热阻；R34为滚珠和内圈的热阻；R45为轴和内圈的热阻；Rair5为轴和环境的热阻；c1为轴承座的热容；c2为轴承内圈的热容；c3为滚珠的热容；c4为轴承内圈的热容；c5为轴的热容。

如上所述，轴承工作过程是热力耦合过程，其计算包括力学计算和温度计算两部分。在第1节动态接触方程的求解中，需要确定轴承内外圈径向热膨胀差值Δr1和滚珠的热膨胀值Δr2。由式（4）～式（6）可知，Δr1和Δr2取决于内外圈和滚珠的温升ΔTi、ΔTo和ΔTb。由式（42）可知：

若已知轴承发热功率，则由式（27）和式（42）数值计算方法可求得内外圈和滚珠的温升。若tk时刻节点i（i=1，2，…，5）温度为T（k）i，离散时间步长为Δt，则设

式（44）代入式（42），整理矩陣得

AT（k+1）=BT（k）+P+Q（k）（45）

其中，系数矩阵A和B为N×N的方阵，其对角元素为

非对角元素与节点间连接热阻有关，若第i个节点与第il个节间连接热阻值为Rj，则有

若节点间无热阻连接，则A和B矩阵对应元素为0。在式（45）中P和Q矩阵分别为

整理式（45），可得

T（k+1）=CT（k）+D+E（k）（51）

C=A－1BD=A－1PE=A－1Q（k）

力学计算即求解动态接触非线性方程组，包括：滚珠的几何约束方程式（12）和式（13），滚珠的力平衡方程式（16）和式（17），轴承的力平衡方程式（24）～ 式（26），共4×Z+3个方程，可解得4×Z+3个参数。动态接触模型求解即求解如下非线性方程组：

F（x）=0（52）

x=［x1x2…x4Z+3］T∈R4Z+3

轴承热力耦合分析数值计算方法的流程如图6所示。

3 试验及计算结果

进行试验以评估滚珠丝杠进给系统轴承部件在工作状态的发热特性，试验对象为HTC2050i数控车床的z轴滚珠丝杠进给系统，数控系统为FANUC 0i Mate-TD，最大进给速度为2400 mm/min。滚珠丝杠采用一对角接触滚珠轴承背靠背放置，采用的轴承为NSK公司的25TAC62B滚珠丝杠专用轴承，轴向预紧力1500 N，环境温度25 ℃。试验测量点放置如图7所示，使用磁性吸附式热电偶检测轴承座上表面的温度，收集从热电偶获得的温度。当电机转速为1000 r/min和1500 r/min时，对进给系统工作过程远离电机的轴承表面温度进行了测量，分为系统工作和自然冷却两个阶段。

为了研究评估滚珠丝杠进给系统轴承部件在工作状态的发热特性，本文研究的轴承为NSK 25TAC62B滚珠丝杠专用轴承，具体参数见表1。

上述计算方法即为复杂工况下的轴承热力耦合计算模型，同时考虑了温升热膨胀对接触计算模型的影响。轴承内部摩擦引起的热效应使轴承部件升温，将引起滚珠和内外圈的热膨胀从而导致轴承内部接触参数改变，同时温升引起的润滑油运动黏度变化对摩擦生热同样存在影响，如式（32）所示。因为润滑剂的黏温效应，润滑剂运动黏度随着轴承内部温升变化，如表2所示。将表中数据插值拟合，代入仿真计算程序。

基于本文所述热力耦合模型进行仿真计算，图8显示了不同转速相同预载荷工况下，仿真模拟的轴承座表面温度（图5中节点1）与试验结果的对比。由图8可以看出，预测的温度与试验测量的温度吻合较好，温度迅速上升，然后趋于恒定，验证了本文提出的热力耦合分析模型的有效性。

轴承热力耦合计算的结果如图9～图12所示。由图9可见，当转速为1500 r/min、轴向载荷为1500 N、径向载荷为50 N时，环境温度25 ℃，轴承组件温度随系统运行时间的增加而升高，并逐渐趋于热平衡状态；轴承内部滚珠的温升高于内外圈的温升，轴承系统逐渐接近热平衡，内外圈温差逐渐减小，但内外圈与滚珠温差小于4 ℃。

由图10可以看出，滚珠接触角以径向载荷作用线为中心线呈对称分布，且对称点的滚珠接触角最大，随着滚珠远离对称点，接触角逐渐减小，且对于每个滚珠与内滚道，接触角始终大于滚珠与外滚道的接触角。在轴承同一位置，滚珠与内滚道接触角随轴承温度的升高而增大，但温度对滚珠与外滚道接触角的影响很小。

由图11可知，滚珠与内外滚道的法向接触载荷几乎相同，但处于接触角对称分布线上滚珠的法向接触力为接触力分布曲线的极大值点，而处于径向作用线反向点为最大值点，滚珠与滚道的法向接触力随温度升高略有降低，但轴承内部接触参数随角位置的变化规律不受温度影响。同时说明轴承内部温度场对轴承内部接触参数和载荷存在明显的影响。轴承温升显著影响轴承受力状态，导致轴承内部结构的变形，因此建立轴承计算模型应当考虑热效应的影响。

由图的12b可以看出，轴承总发热功率随系统工作时间的增加迅速趋近于稳定值，原因一是润滑油黏度随温度升高而减小，另一个原因是由于滚珠与滚道接触的接触载荷随轴承温度升高而逐渐降低，两者综合作用下，使角接触球轴承总发热功率快速达到稳定值，

且与单滚珠发热功率随运动时间变化吻合较好，如图12a所示。

滚珠因自旋发热是轴承热源的重要组成之一，图13所示为轴向载荷和转速对滚珠自旋角速度的影响。当轴向载荷固定，转速从500 r/min增大到3000 r/min时，滚珠自旋角速度随轴承转速的增大而增大；当转速恒定时，随轴向载荷递增的滚珠自旋角速度逐渐降低并趋于稳定值。

轴承发热功率由滚珠与滚道摩擦发热功率、润滑油黏性摩擦发热功率和滚珠自旋发热功率三部分组成。当轴承转速1000 r/min时，轴承各部分发热功率随轴向载荷变化的計算结果如图14所示。可以看出，润滑油黏性摩擦发热功率不受轴向力影响，与转速和温度有关；而滚珠与滚道摩擦发热功率和滚珠自旋发热功率随载荷增大而近似于线性增长。

图15显示了转速3000 r/min时不同轴承轴向载荷下计算的有径向载荷和无径向载荷的轴承发热功率和分布的结果。在外径向载荷作用下，在轴承施加径向载荷时，滚动体与滚道接触区的发热功率近似呈余弦曲线。相反，在没有外部负载的情况下，所有接触区域的发热功率值相同。在联合载荷作用下，轴承内部发热量不均匀，因此已知轴承工况下的载荷分布计算出的发热功率才是准确的。

当轴承转速3000 r/min、轴向载荷1000 N、径向载荷50 N时，力矩载荷大小和方向对轴承接触参数的影响如图16所示。可以看出，正向力矩载荷可以克服径向载荷造成的滚珠与滚道接触角的不均匀性，但反向力矩载荷使得径向载荷造成的滚珠与滚道接触角的不均匀性加重，表明力矩载荷对滚珠与滚道法向接触力的不均匀性起调节作用，对接触角的不均匀性也起到相同的调节作用，可以合理分配每个滚珠的受力，有效改善轴承内部的局部过热现象，延长轴承的使用寿命。

4 结论

本文提出了数控机床进给系统成对安装轴承在实际工况下的热力耦合分析模型。该模型分为两个子模型：拟动态力学模型、瞬态热网络传热模型，该计算模型考虑了润滑剂的黏温效应和温升热膨胀的影响，通过仿真分析以及试验可得出以下结论：

（1）轴承组件温度随系统运行时间增加而升高，并逐渐趋于热平衡的稳定状态，滚珠的温度高于内外圈温度，且内圈温度高于外圈温度，随系统运行时间增加轴承系统逐渐接近热平衡。

（2）当轴承系统存在径向载荷时，各滚珠与滚道接触角随角位置变化的分布曲线是类波浪形曲线。随时间增长轴承内部温度逐渐升高，温升致使内外圈接触角发生变化；滚珠与滚道的法向接触力随温度升高略有减小，但轴承内部接触参数随角位置的变化规律不受温度影响。同时在温度热效应影响下，轴承的摩擦发热功率逐渐减小然后逐渐趋于稳定。

（3）联合载荷作用下，力矩载荷为正方向时，接触载荷分布差异性变小，每个滚珠的受力变得更为均匀。合适的非均匀预紧载荷有利于延长轴承寿命，可以合理分配每个滚珠的受力，有效改善轴承内部的局部过热现象。

（4）通过仿真模拟计算得到进给系统工作过程中轴承部件温度随时间的变化曲线，通过试验检测表面轴承座温度，验证了本文热力耦合分析计算方法的正确性。所提出的方法可以有效预测数控机床滚珠丝杠进给系统轴承部件的内部接触特性以及热力学行为。

参考文献：

［1］ KHONSARI M M. A Review of Thermal Effects in Hydrodynamic Bearings. Part Ⅱ：Journal Bearings［J］. ASLE Transactions， 1987， 30（1）：26-33.

［2］ WEN J， KHONSARI M M， HUA D Y. Three-dimensional Heat Transfer Analysis of Pin-bushing System with Oscillatory Motion：Theory and Experiment［J］. Journal of Tribology， 2011， 133（1）：011101.

［3］ MA F， LI Z， QIU S. Transient Thermal Analysis of Grease-lubricated Spherical Roller Bearings［J］. Journal of Tribology International， 2016， 93：115-123.

［4］ TAKABI J， KHONSARI M M. On the Thermally-induced Seizure in Bearings：a Review［J］. Tribology International， 2015， 91：118-130.

［5］ 趙春雨，侯森林，李朕均. 进给系统成对安装的角接触球轴承热分析［J］. 东北大学学报（自然科学版）， 2020，41（5）：700-705.

ZHAO Chunyu， HOU Senlin， LI Zhenjun. Thermal Analysis Toward Pair-installed Angular Contact Ball Bearings in Feed Systems［J］. Journal of Northeastern University （Natural Science）， 2020，41（5）：700-705.

［6］ JONES A B. Ball Motion and Sliding Friction in Ball Bearing［J］. Journal of Basic Engineering， 1959， 81（3）：1-12.

［7］ HERNOT X， SARTOR M， GUILLOT J. Calculation of the Stiffness Matrix of Angular Contact Ball Bearings by Using the Analytical Approach［J］. Journal of Mechanical Design， 2000， 122（1）：83-90.

［8］ HARRIS T A. Rolling Bearing Analysis［M］. New York：John Wiley， 2001.

［9］ 吴飞科，罗继伟，张磊，等. 关于Hertz点接触理论适用范围的探讨［J］.轴承，2007（5）：1-3.

WU Feike， LUO Jiwei， ZHANG Lei， et al. Discussion on Application Limit to Hertzs Contact Theory［J］. Bearing， 2007（5）：1-3.

［10］ ZHAO C， YU X， HUANG Q， et al. Analysis on the Load Characteristics and Coefficient of Friction of Angular Contact Ball Bearing at High Speed［J］. Tribology International， 2015， 87：50-56.

［11］ TAN L J， HONG J. Nonlinear Thermal Effects on High-speed Spindle Bearings Subjected to Preload［J］. Journal of Tribology International， 2016， 96：361-372.

［12］ BURTON R A， STAPH H E. Thermal Activated Seizure of Angular Contact Bearings［J］. Tribology， 1968， 1（2）：408-417.