基于变论域模糊理论的高低温试验箱温度控制研究

杨洪涛，谢晓杰，于晓周，沈梅

（1.安徽理工大学机械工程学院，淮南 232001；2.安徽理工大学安徽省矿山智能装备与技术重点实验室，淮南 232001）

引言

高低温试验箱是一种用于测试或评定产品或材料在不同温度条件下的适应性、耐久性和稳定性的仪器设备[1]。根据高低温试验箱技术条件GB/T 10592的要求，高低温试验箱在控温小于150 ℃时的稳定状态下箱内温度的变化量不能超过±0.5 ℃、平均温度变化速率≥5 ℃/min[2]，为保证控温精度需要使用PID控制，高低温试验箱在温度控制中使用的方法主要是PID控制法[3]。试验箱工作时的工况复杂，常规PID控制效果不佳，因此需要研究新的PID控制方法。

国内外有学者对试验箱控温及其他PID控温方式进行了研究。王怀光等将增量式PID控制应用于试验箱的温控系统[4]。方忠诚等利用分段式便增益PID控制环境试验箱[5]。解家顺等对试验箱的内部流场进行了研究，并分析了流场对于温度的影响,给出了试验箱的最佳送风风速[6,7]。刘咸贺等提出了一种居于偏差组合专家的PID控制策略，并将其应用于超薄非晶合金的生产过程[8]。Liu等设计了基于ALD过程的PID算法研究，并验证了其有效性和实用性[9]。Xu等提出了一种基于麻雀搜索算法的温度控制策略，并将其用于电池系统，该方法动态性能好，抗干扰能力强[10]。高低温试验箱的工作状态会受到多种因素的影响，例如工作电压、工作电流、散热条件、环境条件等。这些因素在控温过程中相互作用，导致试验箱的控温过程表现出非线性和热惯性等特点，是一种典型的非稳态过程。因此要实现试验箱高精度控温仍是一个技术难题[11-12]。

本文针对试验箱温度控制存在的问题，提出了一种基于变论域理论的模糊PID的高低温试验箱控温方法，实现PID参数的实时调节，以解决试验箱控温时超调量高，调节时间过长等问题。

1 高低温试验箱的控温原理与加热模型

1.1 试验箱工作原理

高低温试验箱的结构由箱体、制冷系统、加热系统、控制系统和温度传感器等组成，如图1所示。由温度传感器采集箱内实时温度，与设定温度比对获取温度差值，输入PID算法进行运算得到控制量，转变为PWM信号控制加热或制冷系统开关的通断时间，最终实现温度的精确控制。本文研究的高低温试验箱低温控制和高温控制采用不同的控制方式。低温(≤47 ℃)控制时，采用加热和制冷系统协同控制实现，其控制精度及响应速度较快。高温(＞47 ℃)控制时，为了节约能耗，仅采用加热系统进行温度实时控制，因此存在较大超调量和稳定速度慢问题，高精度控制更难实现，因此必须研究改进型的PID算法加以精确控制，本文针对高温控制难题开展研究。

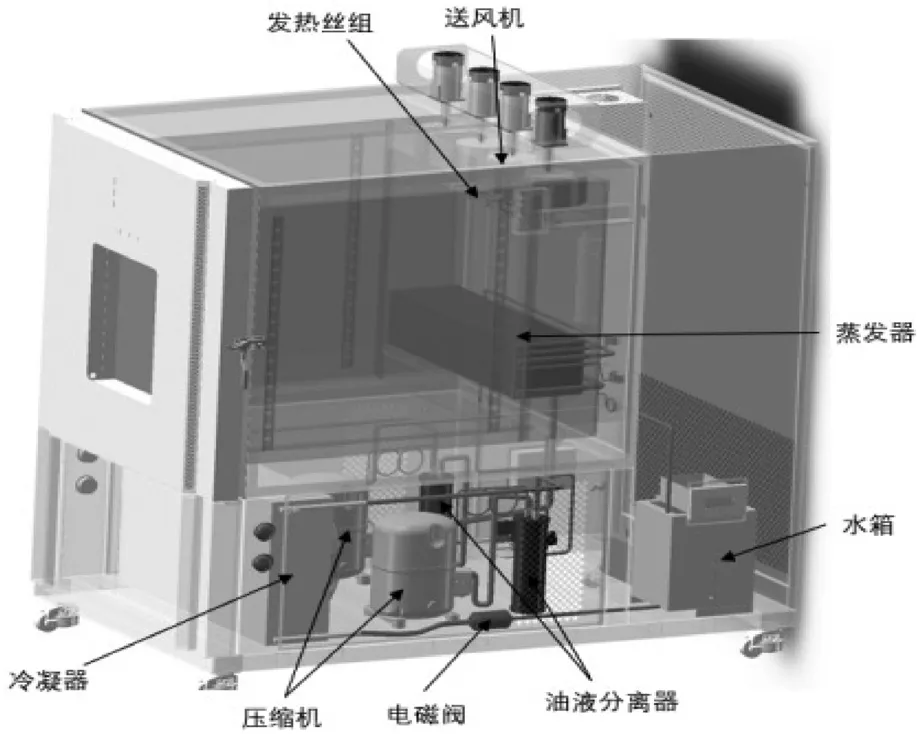
图1 高低温试验箱结构

1.2 试验箱测点选择

为了精确反映试验箱内部温度场分布及精确测量箱内的温度，为后续温度的精确控制打下基础，本文根据研究的试验箱结构尺寸建立了三维仿真模型，放置测试物体于箱内空间，设定加热风速为5 m/s，采用Fluent和标准k-ε湍流模型进行仿真计算，得到的试验箱流场分布如图2所示。从图中可以看出，要真实测量试验箱内部的实际温度，最少必须在ABCD四点布置温度传感器进行实时测量，测量结果取四点的平均值。

2 变论域模糊PID温度控制器设计

2.1 变论域模糊PID原理

PID控制器由比例（P）、积分（I）、微分（D）三个部分组成，其表达式可用以下公式表示：

常规PID的结构简单，局限性较大。相对于传统的PID控制器，模糊PID控制器具有实时调整PID参数的能力，并且利用模糊逻辑规则来处理不确定性，从而有效地适应控制系统的变化。然而，模糊PID控制器的结构一旦确定后，其输入输出论域的划分是固定的。当输入量超过基本论域的范围，或者输入量过小时，模糊控制规则可能无法充分发挥作用，进而对控制效果产生影响。因此引入变论域的思想，当控制系统的输入误差减小或增大时，引入伸缩因子（α、β）自适应的使论域也随之缩小或增大[13]。

假设输入变量e、ec的初始论域分别为[-E，E]和[-EC，EC]，输出变量u的初始论域为[-U，U]，引入伸缩因子后各个变量的论域分别为[-αeE，αeE]，[-αecE，αecE]和[-βU，βU]。论域变化原理如图3所示。

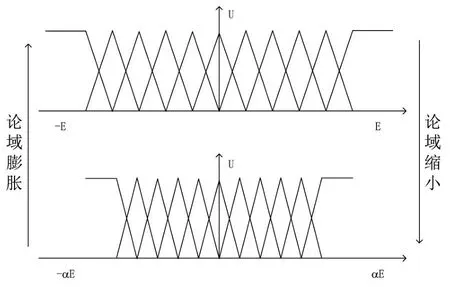
图3 变论域原理

2.2 变论域模糊控制器结构

变论域模糊PID控制结构如图4所示。图中e为设定温度与实际温度的误差值，e为误差值的变化率，αe、αec、β分别为模糊控制规则输入和输出的伸缩因子，控制规则基于e和ec的共同作用实时推理出论域的伸缩因子，改变输入输出变量的论域进而再确定PID三个参数的变化量ΔK，实现PID三个参数的自整定。

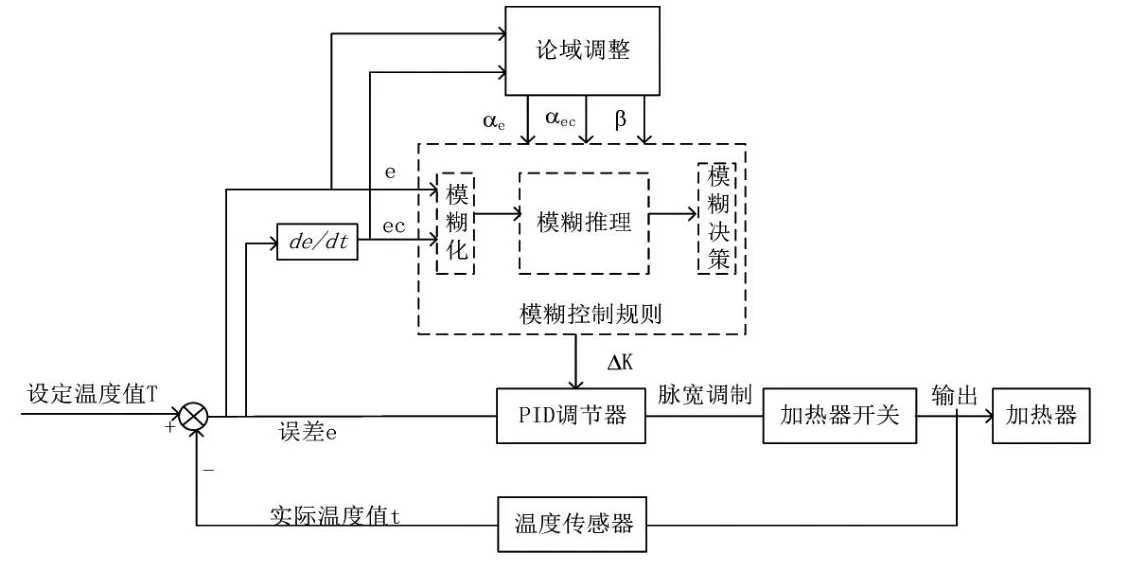
图4 变论域模糊PID控制结构

2.3 自适应伸缩因子设计

变论域模糊控制器的伸缩因子选择直接决定了控制器的控制效果[14]，伸缩因子的选择主要有基于模糊推理、基于误差分级和基于函数模型等方法[15]。综合比较各种伸缩因子选择方法，本文采用的是基于函数模型的自适应伸缩因子，通过误差和误差的变化率实时调节伸缩因子，常见的函数模型伸缩因子有以下两种：

式中：

e—误差；

τ、λ、k—伸缩因子设计参数；

δ—充分小的正数。

选择的函数模型需满足对偶性、非零性、单调性、正规性及协调性。本文的函数模型选择为公式（3），在实际控制中，虽然已经有各种研究给出了控制参数τ的大致取值范围，但是不同控制对象之间具有较大的差异，如果控制参数τ的数值设置不合适，就会导致各种控制对象的控制效果出现差异。因此，在选择控制参数τ时，需要充分考虑控制对象的性质和特性，并根据实际情况进行适当的调整，才能达到最佳的控制效果。根据多项文献研究，已经提出多种实时调整的伸缩因子参数，比较各种实时调整的伸缩因子参数，基于误差实时调整的τ的伸缩因子优化效果较为明显[16]。

τ的取值如下：

输入与输出的伸缩因子函数模型为：

式中：

E1、E2—误差e和误差变化率ec的基础论域，为了确保输入变量与输出变量之间的一致性,使τ1与τ2相等。

2.4 模糊处理及控制规则

结合控制经验以及控制需求，对输入输出变量进行模糊化处理。本文以控温至80 ℃为例，温度误差e及误差变化率ec的基础论域分别为[-80，80]和[-10，10]。Kp、Ki、Kd的模糊论域分别为[-0.03 0.03]、[-0.003 0.003]和[-3 3]。根据模糊规则可将e和ec的模糊论域分别设置为[-8，8]和[-1，1]，则e和ec的量化因子均为10；Kp、Ki、Kd的模糊论域均设置为[-3 3]，则Kp、Ki、Kd的比例因子为0.01，0.001和1。

输入变量和输出变量的模糊子集都设置为7个等级，分别为正大（PB）、正中（PM）、正小（PS）、零（ZO）、负小（NS）、负中（NM）、负大（NB），在不影响控制效果的前提下，为便于计算，模糊控制器的输入输出选用相同的三角型隶属度函数。隶属度函数曲线如图5所示。

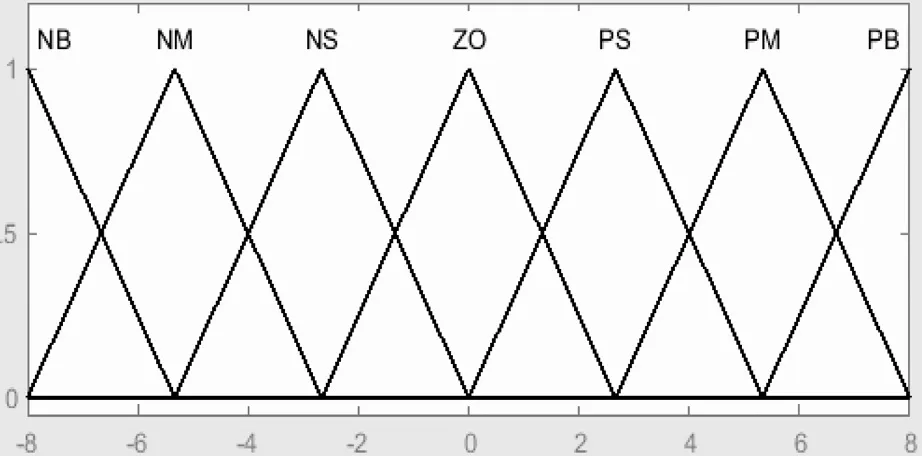
图5 隶属度函数

模糊规则为：控制初始阶段误差值较大，此时增大Kp，减小Ki，限制Kd；控制进程进入中段时误差值为中等大小，此时适当减小Ki，取适中的Kp和Kd；控制进程接近目标值时误差较小，适当减小Kp，增大Kp和Kd。模糊控制规则如表1所示。

根据模糊控制规则对模糊输出量进行处理，将其转化成真实的控制量，得到PID三个参数变化后的最终值，修正后的PID参数值分别为：

式中：

Kp0、Ki0、Kd0—前一个采样周期的PID参数；

△Kp、△Ki、△Kd—解模糊后的PID参数增量；

Kp、Ki、Kd—更新后的PID参数。

3 建模与仿真分析

3.1 试验箱加热数学模型

高低温试验箱的数学模型为一阶惯性传递函数：

在实际控制中该一阶惯性模型还需要加入延迟变量，因此高低温试验箱的传递函数可用一阶惯性加纯滞后的模型来表示，使用MATLAB系统辨识工具箱得到其一阶惯性滞后的数学模型为公式（8）。

3.2 仿真分析

控制器流程如图6所示，控制器系统根据目标值与系统输出值循环执行各个模块。

图6 变论域模糊控制器流程

根据控制器流程并使用Simulink工具箱搭建常规PID、模糊PID及变论域模糊PID控制器仿真模型，模型如图7所示。

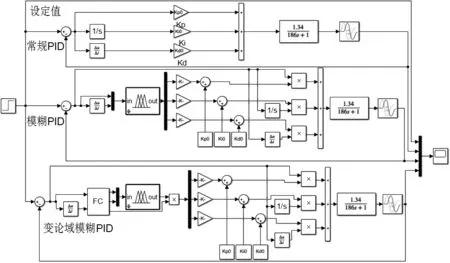
图7 变论域模糊PID控制器仿真模型

控制器的输入信号为阶跃信号，目标值设置为80 ℃，仿真时间设置为1500 s，根据PID参数的Z-N整定法，PID参数的初始值Kp、Ki、Kd分别设置为0.98、0.007、18.62。控制器仿真结果如图8所示。

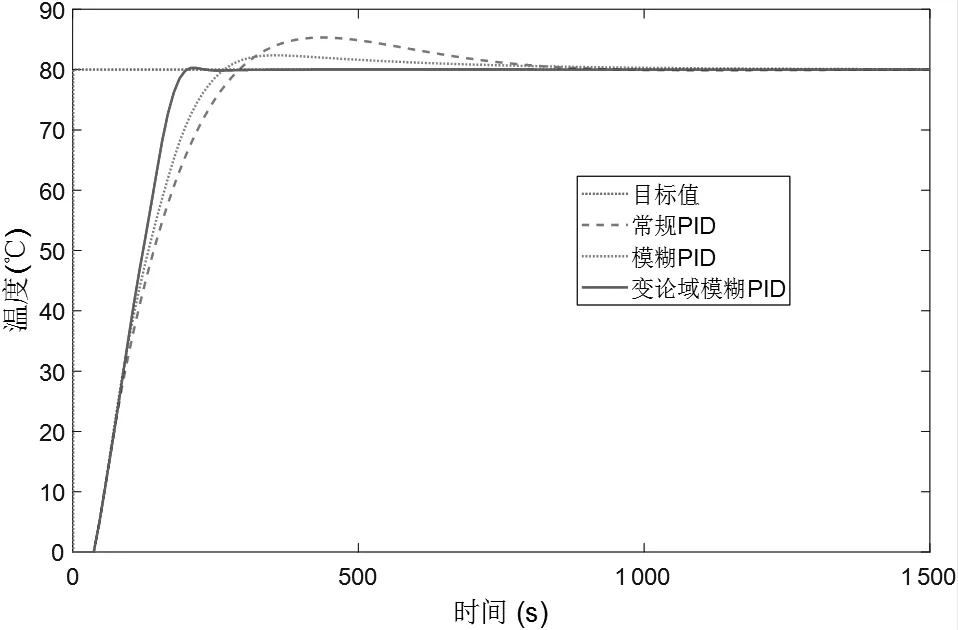
图8 仿真曲线

通过仿真结果可以得到变论域模糊PID、模糊PID和常规PID控制的相关指标，如表2所示。仿真结果表明变论域模糊PID控制器能够有效的降低控温系统的超调量和调节时间。

表2 仿真结果

4 实验验证

4.1 实验装置

本文采用的控温系统原理如图9所示，控制系统由PLC和PC机组成，数据采集系统由PT100铂电阻温度传感器和数据处理模块组成。

图9 控制电路原理

高低温试验箱的型号为LJPTH-100。PLC的型号为XC3-24R-E，测温点布置根据1.2节确定，以4个测温点的平均值作为试验箱整体温度值。硬件设备及测温点布置如图10和图11所示。

图10 硬件设备

图11 测温点布置

4.2 实验结果分析

图12为三种PID控制器的实验曲线。实验数据指标如表3所示。通过对三个控制系统的超调量和达到稳态的时间进行对比可知，高低温试验箱温控系统的超调量在变论域模糊PID的控制下相较于模糊PID和常规PID分别降低了6.8 %和16.5 %，调节时间分别减少了166 s和349 s。

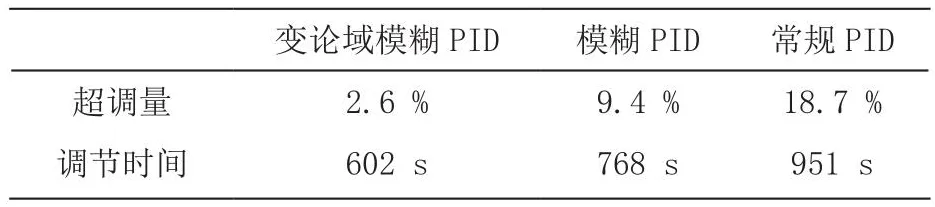
表3 实验结果

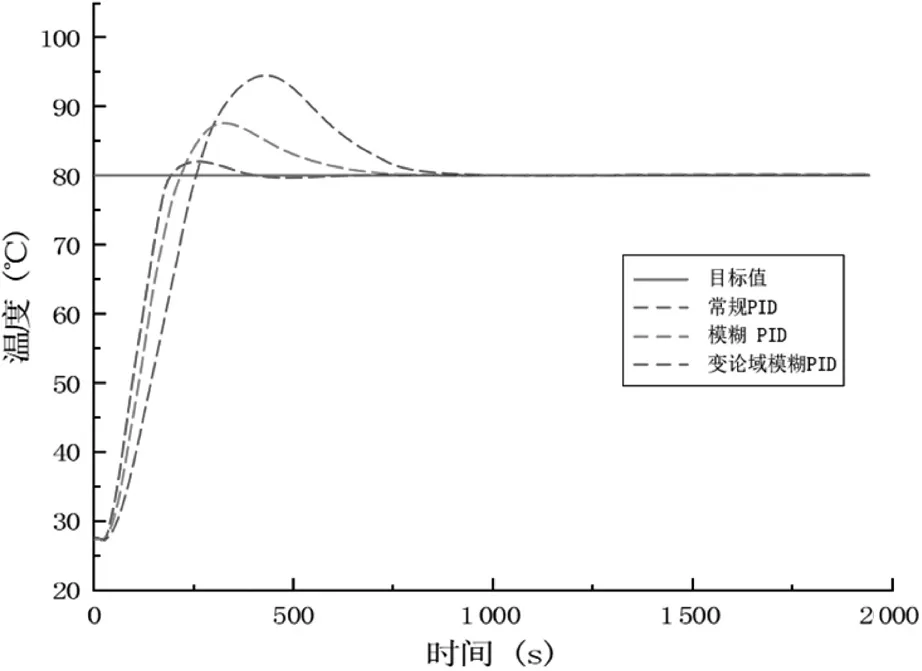
图12 试验曲线

5 结论

通过高低温试验箱的传热原理建立其控温数学模型，设计了自适应伸缩因子并将其与模糊控制理论相结合，利用Simulink工具建立了控制器仿真模型并对三种控制器进行仿真分析，搭建了试验箱实验平台对三种控制器进行了实验验证。

基于变论域模糊控制的高低温试验箱温度控制研究通过仿真和实验证明，该方法能够显著改善试验箱的温度控制性能。采用变论域模糊控制能够降低超调量，缩短调节时间，提高温度稳定性和控制精度。在工业生产和科学研究中高低温试验箱的快速稳定控制能够提供更准确的环境模拟，提高工作效率和生产能力，提高实验数据的可靠性和准确性。变论域模糊控制为高低温试验箱的应用提供了一种可行的控制策略，为控制非线性与非稳态对象的研究与实践提供了有益的参考。