复合材料弯曲性能试验技术研究

金龙，王和，陈国一，孙玉昆，王明，杜一鸣

（天津航天瑞莱科技有限公司沈阳分部，沈阳 110027）

引言

复合材料克服了金属材料质量高、耐高温能力弱、强度低、易氧化等缺点，具有低密度、高硬度、高强度、耐磨损、对裂纹敏感度低、不易发生失效性损坏，因此在众多领域得到了广泛应用。以航空领域为例，在特种飞机中复合材料用量占结构重量的比例最高达到了80 %，航空复合材料性能水平及其在结构中的应用水平，已经成为飞机先进性的一个重要指标[1]。

复合材料的破坏机制及其力学性能的研究宏观上能反映出界面对于复合材料性能的影响，研究复合材料的性能，使其有效地进行材料的设计和加工，需对其破坏机制和力学性能有较深入的了解[2]。通过三点弯曲试验获取的弯曲强度和弯曲模量，能够为材料本构模型的建立和工艺稳定性的研究提供理论支撑，对材料的实际应用具有重要的意义。

1 弯曲试验标准对比分析

针对弯曲试验国内外制定了相应的标准，下文对比分析了国内标准、ASTM标准和EN标准的主要异同点，仅为聚合物基复合材料弯曲性能试验的应用提供参考。

我国现行的GB/T 3356-2014《单向纤维增强塑料弯曲性能试验方法》[3]，该标准适用于连续纤维增强聚合物和其他聚合物基复合材料层合板弯曲性能的测定。由美国材料与试验协会发布的ASTM D 790/D 790M-15《非增强和增强塑料及电绝缘材料弯曲性能》[4]，规定了未增强和增强塑料弯曲性能的测定方法，包括高模量复合材料和电绝缘材料；而ASTM D 7264/D 7264M-15《聚合物基复合材料弯曲性能标准试验方法》[5]用于测试聚合物基复合材料的弯曲性能。EN 2562-97《碳纤维增强塑料-单向层压板平行于纤维方向弯曲试验》[6]规定了碳纤维增强塑料-单向层压板平行于纤维方向弯曲性能；而EN 2746-98《玻璃纤维增强塑料-弯曲试验-三点弯曲方法》[7]主要应用于玻璃纤维增强塑料的弯曲性能测试。

对上述标准中的试样材料、尺寸、跨距、加载速率等主要因素进行对比分析，具体见表1。

表1 常用弯曲性能试验标准对比分析

2 弯曲性能参数

弯曲试验的目的是为了确定复合材料在规定条件下的弯曲性能，包括弯曲强度和弯曲模量[8]。通常结构设计不需要进行弯曲试验，弯曲试验获取的性能参数主要用于材料的工艺稳定性。弯曲试验常用试验方法包括三点弯曲和四点弯曲，本节仅针对三点弯曲试验方法进行研究概述。

2.1 弯曲强度

在试样承受弯矩作用时，中性层既不受拉也不受压，因此根据几何关系可推导出：

式中：

ρ—中性层的曲率半径。由胡克定律可知：

这表明任意纵向纤维的正应力与其到中性层的距离成正比。由于内、外力必须满足平衡方程，，可推导出：

式中：

Iz—截面积对中性轴的惯性矩，由此可得纯弯曲时的正应力为：

式中：

L—跨距；

b、h—试样的宽度和厚度。

3.2 弯曲模量

三点弯曲试验中试样变形的微分形式如图1所示。

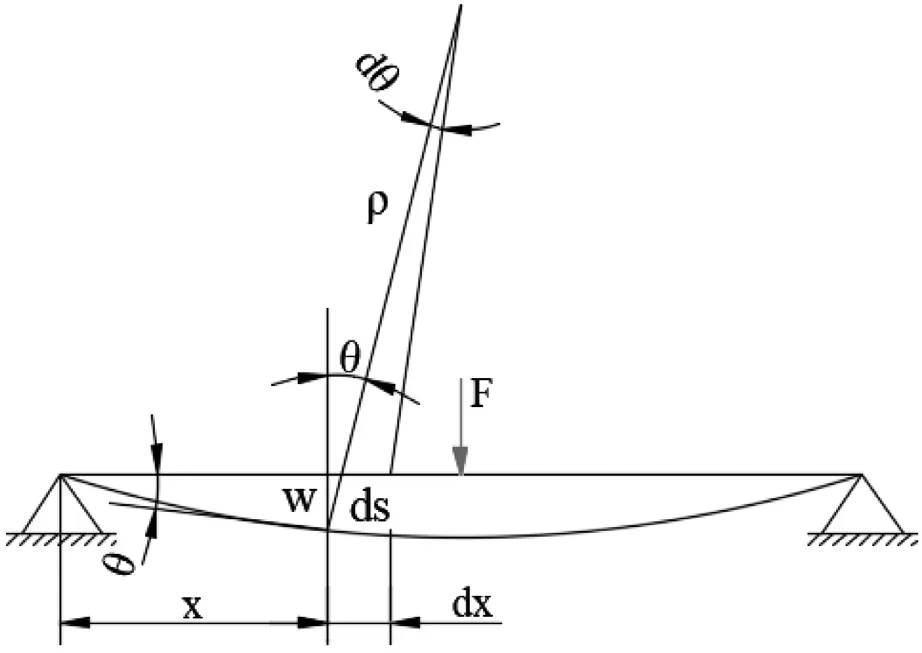
图1 三点弯曲试验中试样变形示意图

弯曲变形中，试样的截面积对其原来位置转过的角度θ，称为截面转角，根据平面假设，弯曲变形前垂直于轴线的截面积，变形后仍垂直于挠曲线，因此截面转角θ就是y轴与挠曲线法线的夹角，故有：

微分弧段ds 两端法线的交点即为曲率中心，因此有：

纯弯曲情况下，根据弯矩和曲率间的关系，于是公式（3）化为：

三点弯曲试验挠度最大值的截面总是靠近跨度中点，所以可以用跨度中点的挠度近似地代替最大挠度，因此中点挠度为：

由此可推导出三点弯曲的弹性模量计算公式为：

式中：

K—载荷-挠度曲线中线性阶段的斜率。

4 三点弯曲试验

试验材料为碳纤维基复合材料，材料宽度18.97 mm，厚度4.375 mm，根据ASTM D 7264中跨距和厚度32∶1的要求，跨距定为140 mm。试验安装状态见图2，使用光栅尺测量试样中心点处的挠度，试验速率为1 mm/min。

图2 三点弯曲试验安装状态

试验载荷-挠度曲线见图3，根据曲线结合公式（5）和（11）求出弯曲强度为450.88 MPa，弹性模量为30.61 GPa。

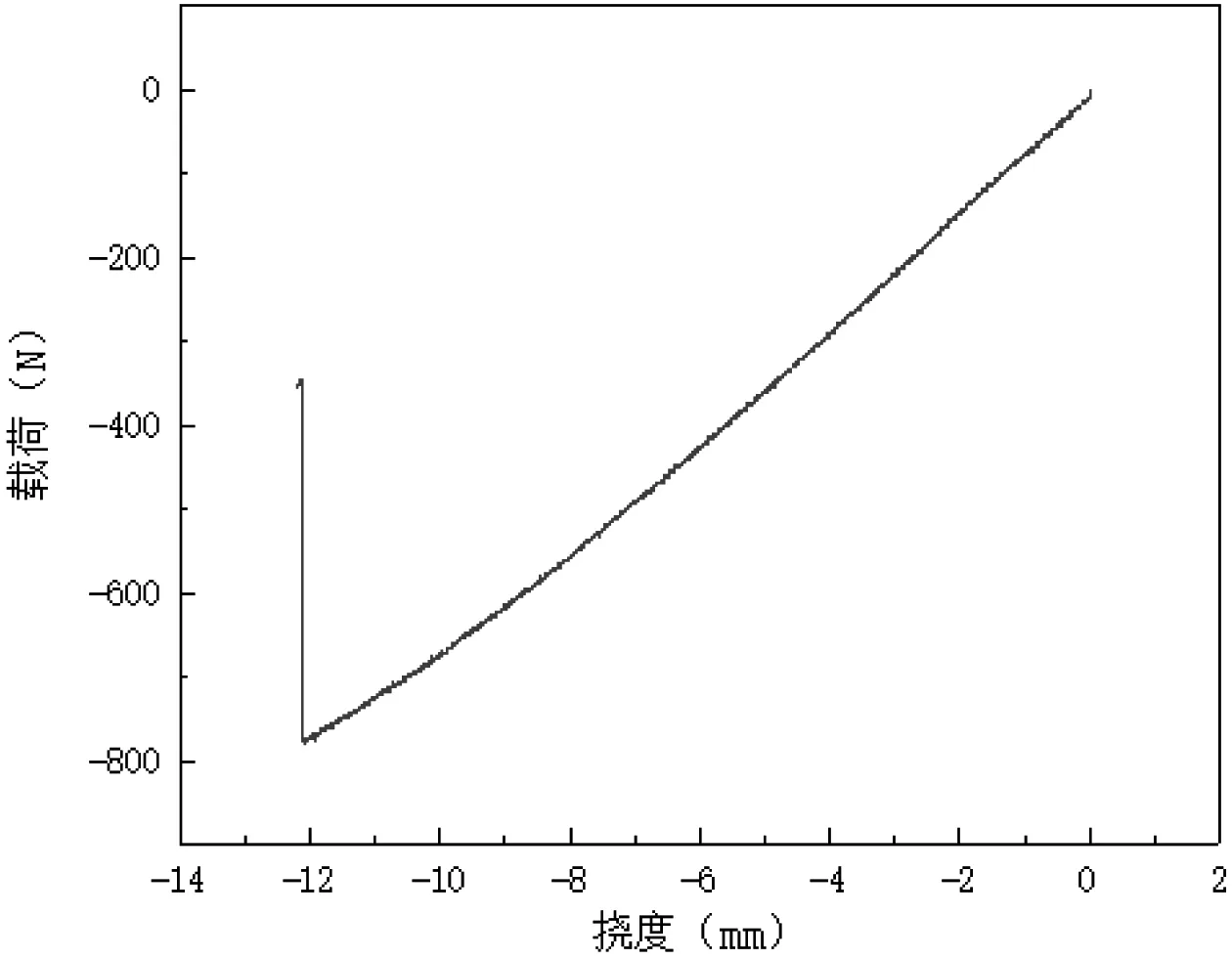
图3 载荷-挠度曲线

4.1 横梁位移的修正

试验全程记录了横梁位移的输出数据，如图4所示，对比载荷-挠度曲线和载荷-位移曲线，可以看出由于试验机和夹具之间存在一定的间隙，导致横梁位移测量的数据略大于光栅尺测量的数据。

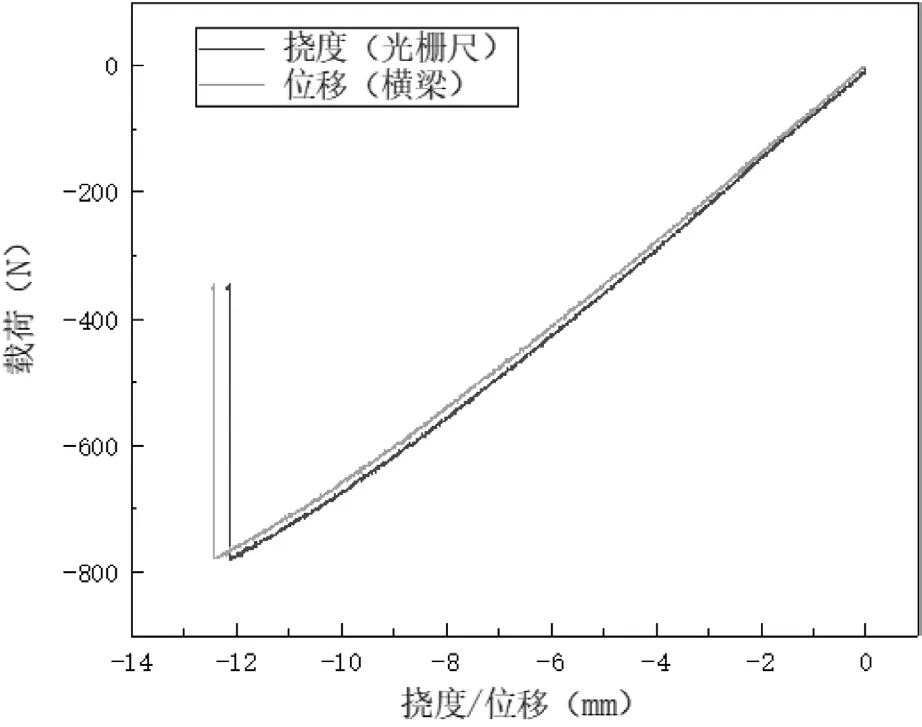
图4 载荷-挠度曲线和载荷-位移曲线对比

通过对横梁位移的数据进行修正，修正系数为0.981，修正后的曲线见图5，可以看出修正后的曲线和由光栅尺测量的载荷-挠度曲线具有很好的一致性，通过对横梁位移修正后的曲线具有一定的参考价值。

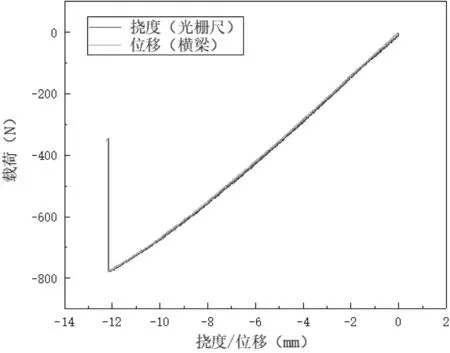
图5 载荷-挠度曲线和载荷-位移曲线对比（修正后）

4.2 力传感器的影响

4.1节中采用的是量程为2.5 KN的力传感器，对相同材料和尺寸的试样，在保证试验条件相同的情况下，使用量程为200 KN的力传感器进行试验，试验曲线见图6。

图6 载荷-挠度曲线（200 KN力传感器）

由曲线可以看出使用大量程的力传感器时载荷数据波动较大，使用ORIGIN软件对数据进行信号处理，处理方法选用Savitzky-Golay，为保证曲线的线性连续多项式选择1阶，窗口点数为200。如图7所示，将信号处理后的曲线和使用2.5 KN力传感器的测试数据进行对比，结果显示出较好的一致性，表明力传感器的量程对试验结果影响较小。

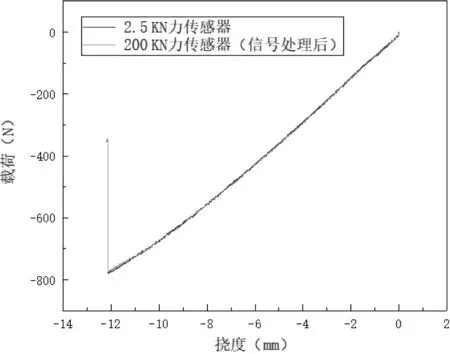
图7 载荷-挠度曲线对比（2.5 KN和200 KN的力传感器）

5 结束语

通过对弯曲试验标准的分析、理论计算及试验验证，得出以下结论：

1）对比了国内外常用的弯曲试验标准，给出了各个标准的适用范围，对标准中关于试样材料、尺寸、跨距、加载速率等主要因素进行对比分析，各标准在试验方法上不尽相同，同时也存在一些差异。

2）对三点弯曲试验中关注的弯曲性能参数，即弯曲强度和弯曲模量的计算公式给出了理论推导。按照ASTM D 7264对碳纤维基复合材料进行三点弯曲试验，根据公式计算其弯曲强度为450.88 MPa，弹性模量为30.61 GPa。

3）对横梁位移的数据进行修正，修正系数为0.981，修正后的曲线和由光栅尺测量的载荷-挠度曲线具有很好的一致性，通过对横梁位移修正后的曲线具有一定的参考价值。

4）使用ORIGIN软件对200 KN力传感器获取的载荷数据进行信号处理，处理方法选用Savitzky-Golay，多项式选择1阶，窗口点数为200，信号处理后的曲线和使用2.5 KN力传感器的测试数据进行对比，结果具有很好的一致性。

综上所述，通过文中对试验标准的对比分析，可根据试验材料和测试需求选择相应标准进行弯曲试验。根据弯曲强度和弯曲模量的公式推导，为三点弯曲试验的性能参数计算提供理论依据。对横梁位移数据进行修正后和光栅尺测量的挠度数据具有很好的一致性，结果具有一定的参考价值。使用不同量程的力传感器进行试验时，通过信号处理后载荷数据基本一致，力传感器的量程对试验结果影响较小。