轮轨接触弹性约束下动力轮对转子系统振动特性分析
周生通, 谢阳泉, 肖 乾, 陈道云, 朱海燕
(1.华东交通大学 载运工具与装备教育部重点实验室,南昌 330013;2.华东交通大学 轨道交通基础设施性能监测与保障国家重点实验室,南昌 330013)
近年来,随着我国高速铁路的快速发展,国内动车组列车的营运速度已普遍提速到300 km/h左右,部分线路实现了常态化350 km/h高标运营,而最新研制的复兴号高速综合检测列车更是在2022年4月21日济南至郑州高铁濮阳至郑州段跑出了单列435 km/h的速度,为我国400 km/h等级的高速动车组列车顺利研制提供重要支撑。作为车辆最终承力部件,动车轮对不但像拖车轮对一样承受来自车体、转向架传递来的全部静动载荷,确保车辆沿钢轨安全走行,还要传递来自牵引驱动装置的驱动力矩,是一个典型的同时存在弯曲、扭转和轴向变形的高速转子部件,具有复杂的弯扭轴振动特性。事实上,在高速运行环境下,动力轮对系统持续受到来自轮轨接触、齿轮啮合以及轴箱轴承等产生的高频冲击振动作用,然而这些高频激励在传统的忽略柔性的轮对刚体模型中是难以被有效考虑的[1]。另一方面,高速带来的轮对转子高速旋转,使得动力轮对系统的旋转陀螺效应变得更加显著,系统模态信息也更加丰富[2,3]。因此,在高速列车动力轮对转子系统的振动特性研究中,充分考虑轮对的柔性、旋转陀螺效应及其约束弹性对准确把握其动力学特性具有重要意义。
列车在轨道上高速行驶时,构成动力轮对系统的轮对、齿轮、轴承等零部件均承受着从车体、钢轨等各方面传递过来的静、动作用力,动力轮对系统从本质上形成了一个复杂的具有弹性变形的动力学系统,而全面把握这一系统的动力学行为,要求能够正确建立充分反映轮对振动特性的精细动力学模型。在传统轨道车辆系统动力学中,轮对通常被模拟为刚体,但刚性轮对仅适用于低频范围(0~30 Hz)内的动力学研究[4,5]。然而,研究发现自下而上传递的轮轨相互作用力中还包含大量的高频激励,相较于传统的刚性轮对动力学模型,考虑轮对柔性的动力学模型更符合高速列车的实际运行情况[6]。目前,关于柔性轮对的建模方法主要有集总参数法[7]、连续体法[8]、传递矩阵法[9]、假设模态法[10]等。但这些轮对建模方法都对模型进行了较大程度上的简化和等效,无法保证模型的完整性和分析的准确性。事实上,随着有限元技术的发展和成熟,适用于复杂结构和边界的有限单元法在轮对建模中逐渐被关注和应用。当前,构建轮对的有限元模型主要有实体模型与梁模型两种。其中实体模型多是借助有限元软件以实体单元离散,然后导入多体动力学软件(如SIMPACK、UM等)中进行轮对刚柔耦合多体动力学仿真研究[11],但实体模型计算成本昂贵且在软件仿真时难以考虑轮对旋转陀螺效应。相比之下,梁单元模拟在满足计算精度的同时还具有计算效率高的特点,在考虑其他因素时单元整合也更为简便。因此,以梁单元模拟轮对的方式也得到了不少学者的青睐。在基于梁理论的轮对建模方面,Liu等[12]以有限元实体模型结果为参照,对比研究了基于欧拉伯努利梁和铁木辛柯梁的传递矩阵方法,发现考虑剪切效应的铁木辛柯梁能更好地反映轮对的动力学固有特性。另一方面,针对高速运行下的轮对陀螺效应,杨柳[13]、王滋昊等[14]基于转子动力学有限元理论以梁单元方式构建了轮对的有限元模型,并分别针对机车牵引传动系统的振动模态分析、偏心状态下轮对转子动力学响应等问题开展研究。不过,现有基于梁理论的轮对转子动力学特性研究中,轮对梁转子模型大多止步于描述弯曲振动的四自由度梁模型,但能够同时描述弯扭、弯轴和弯扭轴等耦合振动特性的五自由度和六自由度梁模型采用较少,使得全自由度下轮对动力学特性研究不足。
此外,高速运行的动力轮对转子受到来自轮轨接触和轴箱轴承的弹性约束作用。在非线性瞬态动力学研究中,这些约束弹性的作用大多被简化为非线性激励力予以考虑[15],但在振动特性研究中则需合理等效线性化为弹簧阻尼元件[16]。例如:王滋昊等在模拟某轮对-车轴系统时就将轴承所在的弹性支承简化为了弹簧阻尼单元,但在固有特性和临界转速研究中未考虑轮轨接触弹性的影响;杨柳等[17]则采用有限元思想将非线性的轮轨作用力和轴承约束力转化为相应的弹簧阻尼单元矩阵。不过,在轮轨接触弹性约束方面,现有研究大多仅考虑了轮轨接触对车轮法向(即垂直于车轴方向)的弹性限制,忽略了车轮踏面锥度引起的轴向接触弹性。
综上所述,本文聚焦现有轮对转子系统在振动特性建模与仿真中的不足,在充分考虑轮对柔性、陀螺效应和约束弹性的基础上,以典型高速列车动力轮对转子系统为研究对象,建立基于铁木辛柯梁转子有限元理论的动力轮对转子系统弯扭轴有限元模型,推导出模拟轮轨约束弹性的线性化有限单元,并详细探讨动力轮对转子系统的弯曲、扭转和轴向振动特性规律以及典型外部激励作用下动力轮对转子系统的共振稳定性问题。
1 动力轮对转子系统有限元模型
1.1 动力轮对结构离散与方程建立
如图1所示,高速列车动力轮对转子部分主要由左右车轮(含轮盘)、车轴和牵引大齿轮组成,并通过位于左右两侧的轮轨关系和轴箱轴承分别与钢轨和转向架结构相接。为了研究动力轮对转子系统的振动特性,将轴箱轴承外圈和钢轨视作固定约束,以梁转子有限元思想进行结构离散,其中,车轴结构离散为梁转子单元,并在轴肩、车轮、轴承、齿轮等位置离散网格;车轮和齿轮结构等效为刚性圆盘单元,附在对应位置节点上;轮轨接触和轴箱轴承的约束弹性则以线性化的弹簧阻尼单元模拟。离散后的动力轮对转子系统有限元模型如图2所示,其中OXYZ为整体坐标系,Z轴沿轮对轴线方向、Y轴沿轮对垂向、X沿轮对纵向。
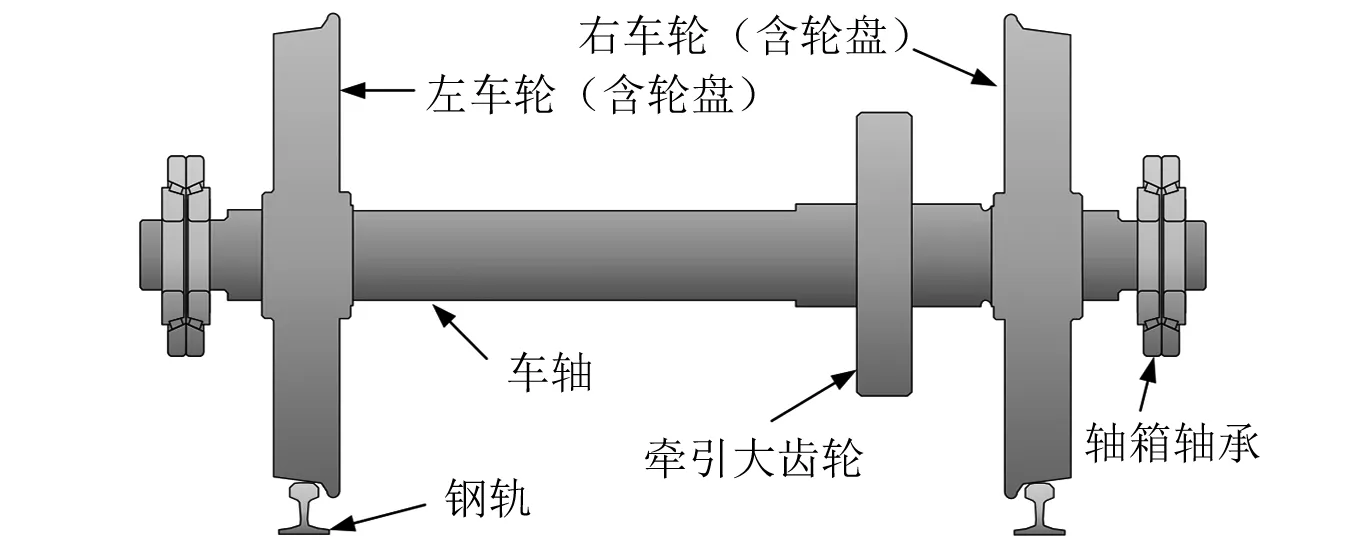
图1 动力轮对结构示意图Fig.1 Structure diagram of power wheelset
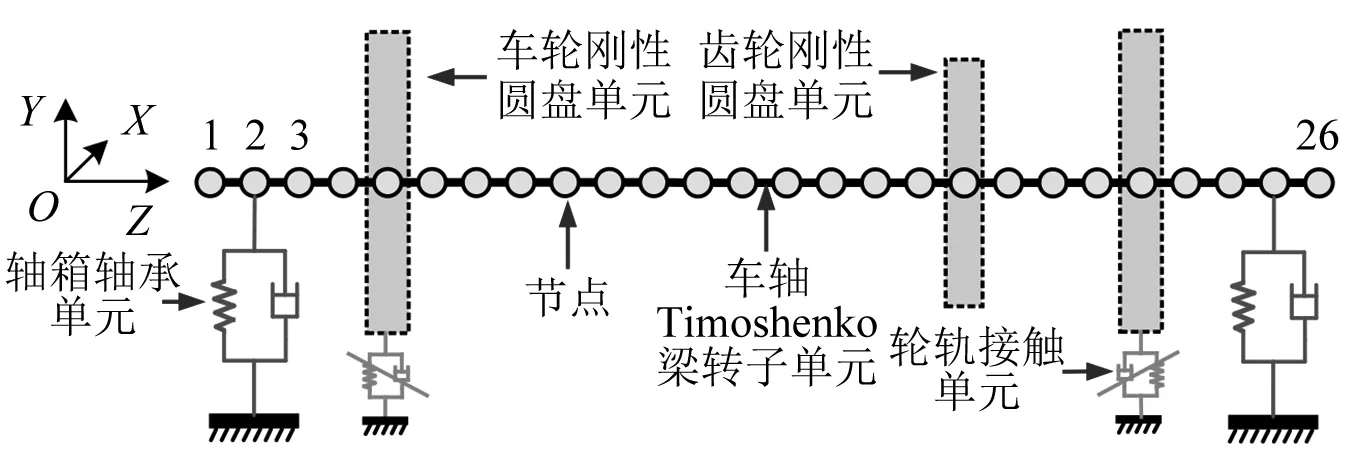
图2 动力轮对转子系统有限元模型Fig.2 Finite element model of power wheelset rotor system
将各单元矩阵组装成整体矩阵,可得动力轮对转子系统的动力学微分方程为
(1)
式中,M,C,K,G和F分别为系统的整体质量矩阵、阻尼矩阵、刚度矩阵、单位转速下的陀螺矩阵以及外力列向量。其中M,G矩阵主要由模拟车轴的梁转子单元以及模拟车轮和齿轮的刚性圆盘单元贡献;K矩阵则除了由车轴贡献外,还包括轮轨接触约束和轴箱轴承约束的弹性贡献;Ω为轮对转速。考虑到本文仅研究动力轮对转子系统的弯扭轴模态特征,故直接令外力向量F=0,且忽略阻尼矩阵C,则可得如下自由振动状态空间方程
(2)

1.2 基于等效圆锥踏面的线性化轮轨接触单元
轮轨接触弹性是影响轮对转子系统振动特性的关键因素。为了方便推导线性化的轮轨接触单元矩阵,这里对轮轨接触关系作一定的简化处理:①车轮踏面被等效为锥角为2α的锥面;②忽略车轮和钢轨的本体弹性以及轮轨切线接触弹性,仅考虑轮轨法向接触弹性;③钢轨接触表面为连续外凸曲面,与车轮等效锥面始终保持单点接触。按照赫兹非线性弹性接触理论,轮轨法向作用力可表达为
(3)
式中:G为轮轨接触常数;δ(t)为轮轨法向接触压缩量。显然,轮轨接触法向作用力是一个非线性函数。为了研究轮对转子系统的模态特性,将非线性轮轨法向力线性化,可获得线性化的轮轨法向接触刚度
(4)
特别地,如图3(a)所示,在任意轴重载荷W作用下,轮轨接触点B将产生法向作用力Fn,若假设相应的轮轨法向接触压缩量为δ0,即δ(t) =δ0,那么由式(3)和式(4)即可得车辆轴重平衡状态下的轮轨法向作用力和线性化接触刚度分别为
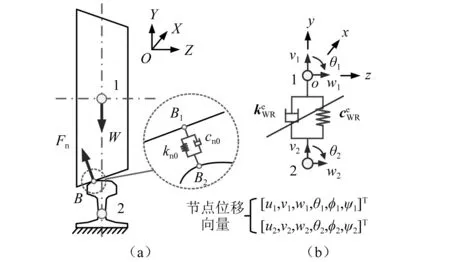
图3 车轮轴向位移下的力学分析Fig.3 Mechanical analysis of wheel under axial displacement
(5)
(6)
显然,该平衡状态下的轮轨接触弹性可由图3(a)中接触点B1和B2间的线性化弹簧阻尼元件(kn0,cn0)表达。但受到接触位置和方位的影响,该等效线性化元件无法直接集成到轮对转子系统方程。
1.2.1 右轮轨接触单元
为了将上述轮轨法向接触弹性引入轮对转子系统有限元方程,这里以右侧轮轨接触为分析对象,定义如图3(b)所示的右轮轨接触单元。其中,节点1位于车轮滚动圆中心,具有六个自由度并定义节点位移向量δ1=[u1,v1,w1,θ1,φ1,ψ1]T;节点2位于钢轨截面质心,同样具有六个自由度且位移向量为δ2=[u2,v2,w2,θ2,φ2,ψ2]T,但由于本文假设钢轨底面固结且不考虑钢轨本体弹性,因此节点2等效于接地,自由度为0。相应地,该轮轨接触单元刚度矩阵是一个6×6矩阵,经推导,单元矩阵形式为
(7)
可以看到单元矩阵中仅在车轮沿y轴沉浮(v)、沿z轴横移(w)和绕x轴侧滚(θ)三个自由度上存在元素,这是由于该单元仅考虑了轮轨法向接触弹性,而该弹性仅在平面oyz内提供刚度贡献。下面分别利用刚度影响系数法和能量法推导该右轮轨接触单元矩阵。
1.2.2 基于刚度影响系数法的单元刚度矩阵计算
按照刚度影响系数法,若使刚体车轮在第j个自由度上产生单位位移而相应在车轮第i个自由度上所施加的力或力矩即为轮轨接触单元矩阵的元素kij。为此,如图4所示,在局部坐标系oxyz下,令车轮沿z向横移自由度发生单位位移w=1,那么由于刚性钢轨约束限制,车轮受到的附加轮轨接触法向反力为
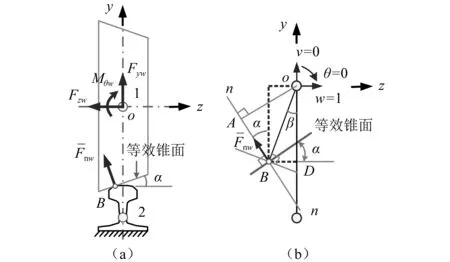
图4 基于刚度影响系数法的右轮轨受力分析Fig.4 Force analysis of right wheel-rail based on stiffness influence coefficient method
(8)
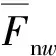
(9)
式中,lOA为局部坐标系原点到接触点法线的距离,大小表达为
lOA=lOBsin(α+β)
(10)
式中,lOB为原点到接触点B的距离;β为OB与y轴的夹角。
同理,使车轮沿y轴和绕x轴分别产生垂向和侧滚方向上的单位位移,即v= 1和θ= 1,同样会在接触点B引起附加轮轨接触法向反力,即
(11)
(12)
显然,由于单位位移v=1和θ=1是减少轮轨接触法线压缩程度的,所以产生的附加反力与w=1时存在一个负号差异。相应地,可得右轮轨接触单元的其余元素
kvv=-Fyv=-Fnvsin(π/2+α)=kncos2α,
kwv=-Fzv=-Fnvcos(π/2+α)=-knsinαcosα,
kθv=-Mxv=-FnvlOA=knlOAcosα
(13)

(14)
此外,若令沿x轴伸缩(u)、绕y轴摇头(φ)和绕z轴点头(ψ)三个自由度分别产生单位位移,即u=1,φ=1和ψ=1,可以看到:由于仅考虑轮轨单点接触的法向弹性,使得这三个方向上的位移并不产生附加的轮轨法向作用力,故而这三个自由度所对应的矩阵元素全为零。
综上,用前述计算的表达式重写右轮轨单元矩阵,同时为简化书写仅保留含非零元素的列与行,有
(15)
1.2.3 基于能量法的单元刚度矩阵计算
若利用能量法推导轮轨接触单元刚度矩阵,则需首先表达出单元势能,进而代入拉格朗日方程实现单元刚度矩阵的推导。如图3(a)所示,轮轨法向接触特性被等效线性化为一个弹簧阻尼元件,因此可按弹簧原理表达单元势能,即
(16)
式中,δn为轮轨相对运动在接触点B处引起的法向压缩量,可由车轮侧接触点B1和钢轨侧接触点B2的相对位移在法线上的投影计算得到。考虑到本文假设钢轨底面固结且不考虑其本体弹性,于是依据刚体上任意一点的位移关系,利用单元节点1的位移表达出接触点B1的位移
(17)
式中,参数b和c分别为接触点B距离单元坐标系y轴和z轴的距离。进一步将位移分解到法线方向,可得由单元节点位移δ1=[u1,v1,w1,θ1,φ1,ψ1]T引起的轮轨接触方向压缩量
δn=wB1sinα-vB1cosα=
(w1-bθ1)sinα-(v1+cθ1)cosα=Tδ1
(18)

将式(18)代入式(16)获得由单元节点位移表达的势能,进一步按照拉格朗日方程可得到单元刚度矩阵
(19)
结果表明式(19)的矩阵运算结果与式(15)相同,即所采用的刚度影响系数法和能量法的推导结果一致。
1.2.4 左轮轨接触单元矩阵
左轮轨接触单元矩阵可采用前述同样方法推导,如图5所示。不过,观察发现:左右轮轨在结构上存在镜像关系,即角度α和β在左、右两轮中的方位恰好是相反的,因此只需将右轮轨接触单元计算公式中的α和β分别用-α和-β替换即可得左轮轨接触单元矩阵,于是

图5 基于刚度影响系数法的左轮轨受力分析Fig.5 Force analysis of left wheel-rail based on stiffness influence coefficient method
(20)
需要指出的是,虽然前述线性化轮轨接触单元是在等效圆锥车轮踏面基础上推导的,但单元矩阵表达式同样适用于车轮真实踏面,应用时仅需利用诸如迹线法等将轮轨接触点B的实际位置确定,并提取接触点的位置信息(如lOB或lBD)和轮轨接触角代入单元矩阵表达式,即可获得对应状态下的线性化轮轨接触单元矩阵。
2 模型求解与结果验证
以某型高速动车组列车的动力轮对为研究对象,按照前述方法建立其梁转子有限元模型。其中车轮质量为393 kg,直径转动惯量和极转动惯量分别为27.3 kg·m2和53.7 kg·m2;大齿轮质量为76 kg,直径转动惯量和极转动惯量分别为1.56 kg·m2和3 kg·m2;轴箱轴承刚度为1×108N/m;车轴弹性模量为205.8 GPa,密度为7 850 kg/m3。在估算轮轨接触单元刚度矩阵时,取轴重15 t,车轮半径0.46 m,等效锥形踏面斜度1 ∶10,轮轨接触点B与车轮质心平面的水平距离lBD=10 mm(见图5)。考虑到我国高速列车还有提速的空间,取假设的车辆行驶速度为400 km/h,换算为动力轮对转子系统转速为Ω=2 298.9 r/min。注:后续凡未明确转速信息的模态结果均是指Ω=2 298.9 r/min时的计算结果。
在前述已知的模型数据基础上,利用自编的动力轮对转子系统MATLAB有限元程序,计算转子的坎贝尔图、模态振型以及前4阶临界转速。同时,为了验证结果正确性,借助ANSYS转子动力学功能模块,添加自定义的轮轨接触单元,建立等价的动力轮对转子系统ANSYS有限元模型,计算模态结果。两种模型结果如图6、图7和表1所示。注: B1和F1分别为第1阶反涡动和正涡动弯曲振型;T1和A1分别为第1阶扭转振型和轴向振型。
图6 两种模型的坎贝尔图对比Fig.6 Comparison of Campbell diagram between two models

图7 两种模型的模态信息对比Fig.7 Comparison of modal information between two models
从图6、图7和表1可以看出,MATLAB模型得到的坎贝尔图及其前4阶弯曲模态(振型和固有频率)和ANSYS模型吻合度较好,且前4阶临界转速也相符合,最大误差仅0.139 %。因此,验证了所编制的动力轮对转子系统MATLAB有限元程序的正确性。
3 弯扭轴模型下模态结果分析
为了更详细地分析0~300 Hz内动力轮对转子系统的弯扭轴模态变化规律,这里进一步设计四种不同自由度的模态模型,即四自由度的弯曲模型(模型1)、五自由度的弯扭模型(模型2)、五自由度的弯轴模型(模型3)以及六自由度的弯扭轴模型(模型4,亦即全自由度模型)。考虑到模型4结果的完备性和篇幅限制,这里仅列出模型4在400 km/h下的模态数据且模态阶数亦按该数据编号,如表2所示。

表2 400 km/m下的模态数据(模型4)
同时,将模型1、模型2和模型3分别得到的坎贝尔图绘制在图8,结合模型4的坎贝尔图(见图6),可以发现:相比仅具有弯曲自由度的弯曲模型1,弯扭模型2的坎贝尔图在所关注的0-300 Hz频率范围内新增了一根70.71 Hz的扭转振动模态频率线,而弯轴模型3的坎贝尔图则是新增了一根63.3 Hz的轴向振动模态频率线,其余模态频率线则是三种模型所共有的弯曲振动模态。进一步,对比图8与图6,可以看到具有全自由度的模型4的频率线涵盖了前三种模型出现的所有频率线,即包含了全部的弯曲、扭转和轴向模态信息,并且具有的固有频率和振型数据也基本保持一致。因此,后续的模态分析均以弯扭轴(模型4)的结果展开讨论。
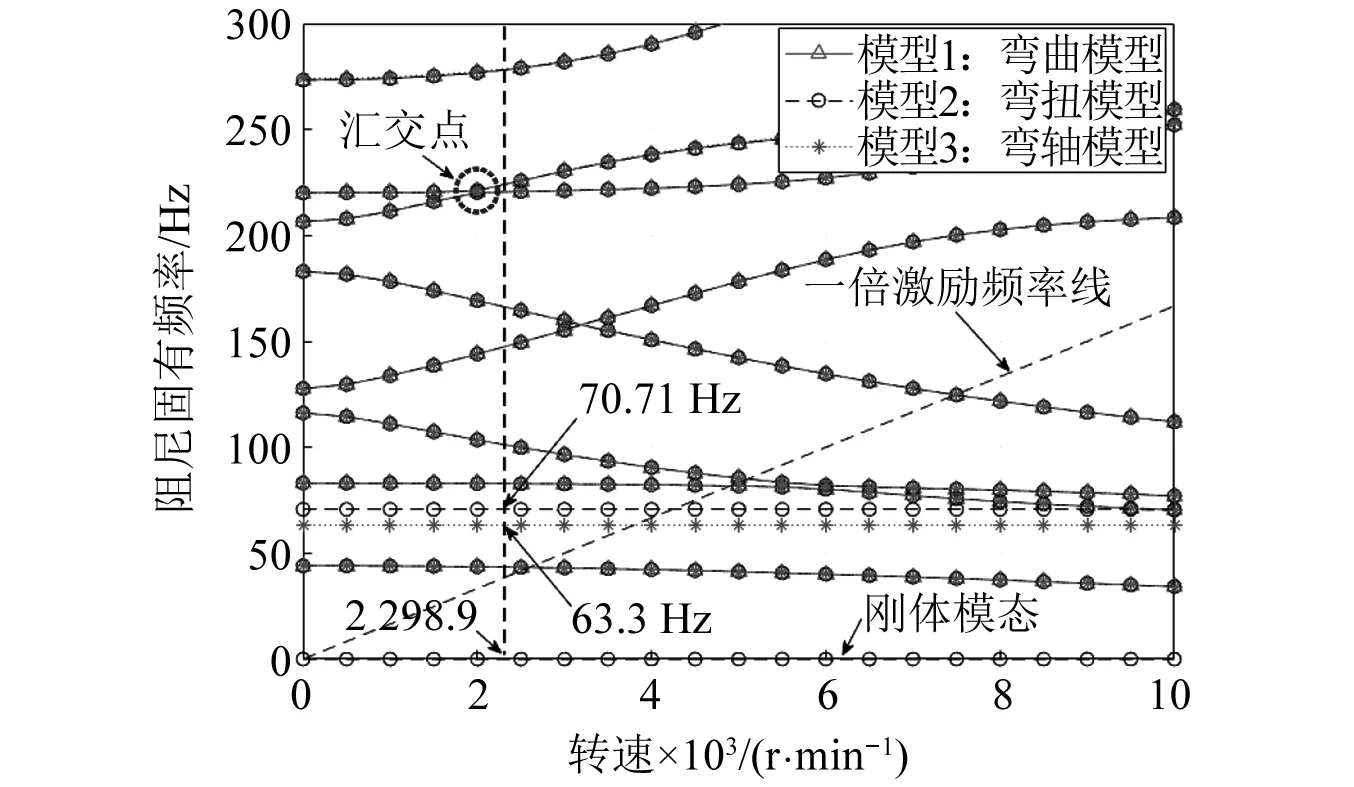
图8 三种自由度模型坎贝尔图对比Fig.8 Campbell diagram comparison of three degree of freedom models
3.1 弯曲模态的涡动轨迹及振型分析
首先,分析动力轮对转子系统弯曲模态的涡动轨迹。图9绘制了左轮(节点5)、右轮(节点22)和大齿轮(节点18)位置处的前4阶弯曲振型涡动轨迹。结合图7和图9可以看到,动力轮对转子的弯曲振型均呈现椭圆状,而且前2阶弯曲振型(B1和B2)还整体表现出了严重的“扁平”状(即椭圆长半轴显著大于短半轴)。究其原因主要是由于轮轨接触约束弹性的存在造成动力轮对转子在垂向(y向)的支承刚度远大于纵向(x向)支承刚度,形成了显著各项异性的支承特性,而且由于左右车轮所在节点位置较大地参与了第1和第2阶弯曲振型(B1和B2),从而使得前2阶弯曲振型的涡动轨迹呈现严重“扁平”状。相比起来,左右车轮位置距离第3和第4阶弯曲振型(B3和B4)的振节较近(见图7),使得轮轨接触刚度引起的支承刚度各项异性影响变弱,相应的涡动轨迹扁平化现象也相应地变弱。结合图7和图9可以发现,当外界激励频率能够激发B1和B2两阶弯曲振型时,动力轮对势必将产生较大的纵向主振动,易出现车轮打滑现象,致使踏面磨损严重;而B3和B4振型激发下,虽然车轮处振动较小,但两端的轴箱轴承位置振动垂向较大,易传递给车体而引起车体垂向的剧烈振动。
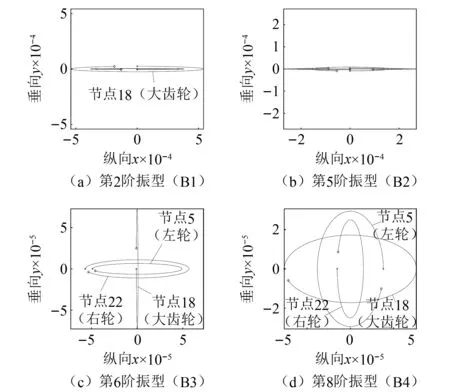
图9 模型4下前4阶弯曲振型涡动轨迹Fig.9 The swirling trajectory of the first four bending modes under model 4

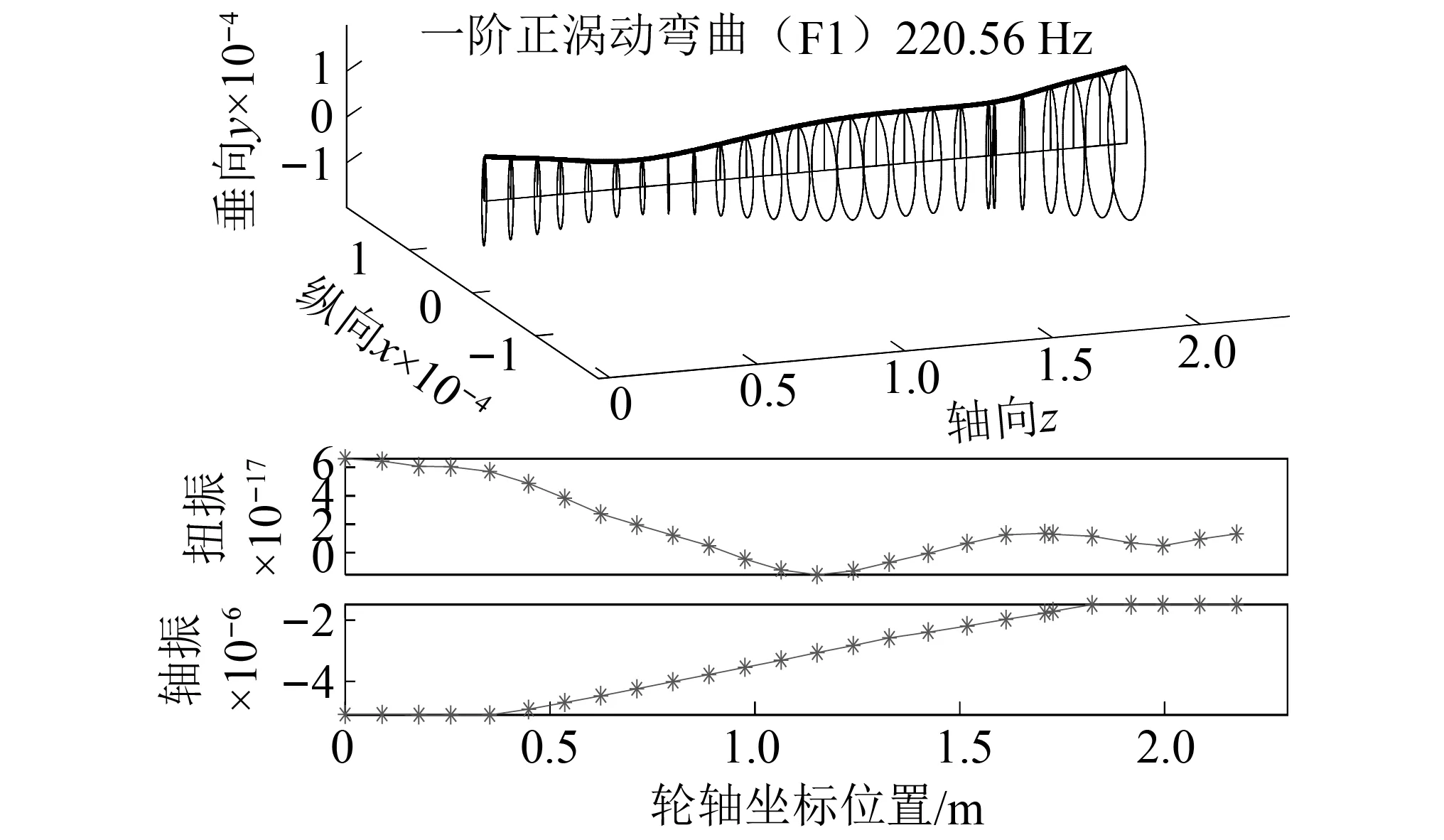
图10 模型4第9阶振型(F1)Fig.10 The 9th mode shape of model 4 (F1)

图11 模型4第11阶振型(F2)Fig.11 The 11th mode shape of model 4 (F2)
此外,观察图10和图11中F1和F2弯曲振型包含的扭转和轴向振动情况,可以发现轴向振动(量级在10-6)明显大于扭转振动(量级在10-17或10-18),更接近弯曲振动(量级10-5),这一现象同样出现在其他阶振型中,表明实际中弯轴振动耦合将会明显高于弯扭振动耦合。这一现象可以解释为:因为轮轨接触存在一定倾角,使得轮轨接触垂向和轴向刚度存在较大耦合关系,当车轮受到垂向力的作用下,通过接触倾角产生轴向的分力,进而引起轴向的振动,因此,轴向和弯曲振型的同时出现符合实际情况,而扭振则难以伴随弯曲、轴向振动一起出现。此外,不难推断出,由于轮轨接触刚度的垂向和轴向耦合关系,使得振型的弯轴振动耦合明显,同时具有较大的轴向(即对应车体横向)和垂向振动,这势必将影响车辆的抗倾覆稳定性、蛇形稳定性等性能评估。
3.2 模态频率线汇交处的振型分析
从图6可以看到,当动力轮对转子转速处在2 000 r/min附近时,模型4的第9阶振型和第10阶振型对应的频率线发生交汇,这种情况同样存在于模型1~3(见图8)中。由于该位置所处的车辆实际行驶速度与当前我国350 km/h十分接近,即接近列车实际的复杂高频运行环境,因此有必要对交汇位置附近的轮对转子振型作深入分析。
图12展示了模型4中转速在2 000 r/min附近动力轮对转子的第9、第10阶振型演变情况。理论上讲,两者应在频率交叉点处发生振型交换,但从图12中可以看到,随着转子转速的提升,在1 881~1 991 r/min内,原本处于第10阶的1阶正涡动弯曲(F1)消失,使得4阶正涡动弯曲振型(F4)同时存在于第9、10阶振型。此时,1阶弯曲振型仅剩1阶反涡动弯曲振型(B1)存在于第2阶,而4阶弯曲则由于交汇的影响同时出现在3阶振型中(即第8阶的四阶反涡动弯曲振型和第9、第10阶的4阶正涡动振型)。由于消失的1阶正涡动弯曲共振主要表现在垂向上(见图12(b)),易加剧车辆垂向振动,而加倍出现4阶正涡动弯曲共振在两车轮处主要表现在纵向涡动,使得车轮更易磨损。因此,可以预测在该交汇频率范围内若存在高频激励激发相应共振,则车轮踏面损伤的可能性将会显著增加。

图12 频率汇交处振型变化情况Fig.12 The change of vibration mode at frequency intersection
3.3 扭转和轴向模态的振型分析
作为传递驱动力矩和确保列车沿钢轨走行的关键部件,动力轮对转子的扭转和轴向振动模态对高速列车动力学性能同样存在着重要影响,应避免正常工况下可能存在的共振问题。图13和图14分别绘制了模型4的扭转振型以及轴向振动振型,结合图6和表2可以发现:该动力轮对转子的轴向振型和扭转振型出现的阶次非常接近,基本上是在一前一后两个相邻的振型,例如T1(70.71 Hz)在A1(63.3 Hz)之后的1阶振型出现,A2(588.78 Hz)在T2(568.47 Hz)之后出现,但到T5(第32阶振型,3 370.32 Hz)和A5(第41阶振型,4 695.21 Hz)时不再出现这种情况。
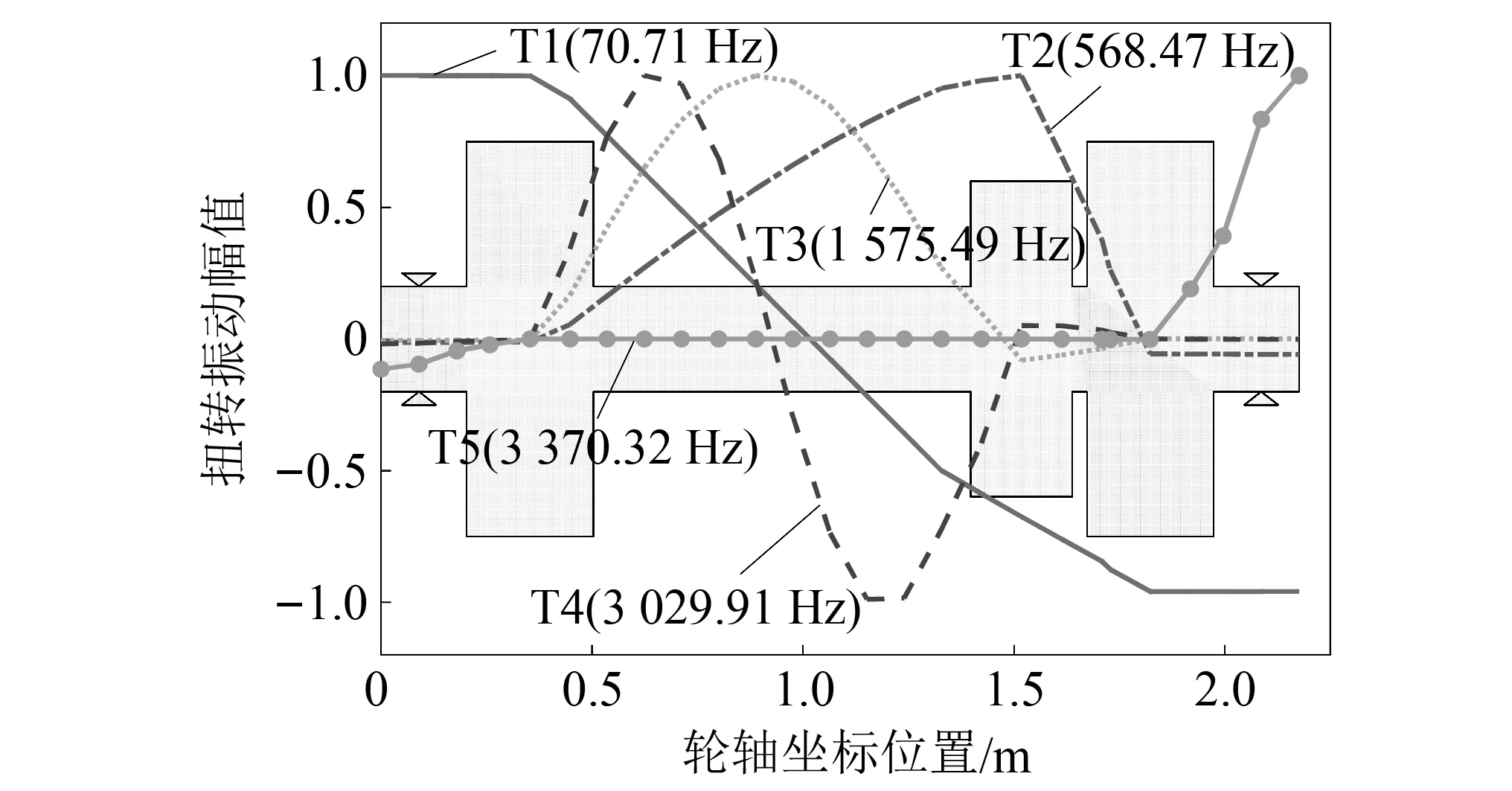
图13 模型4的扭转振型Fig.13 Torsional mode shapes of model 4
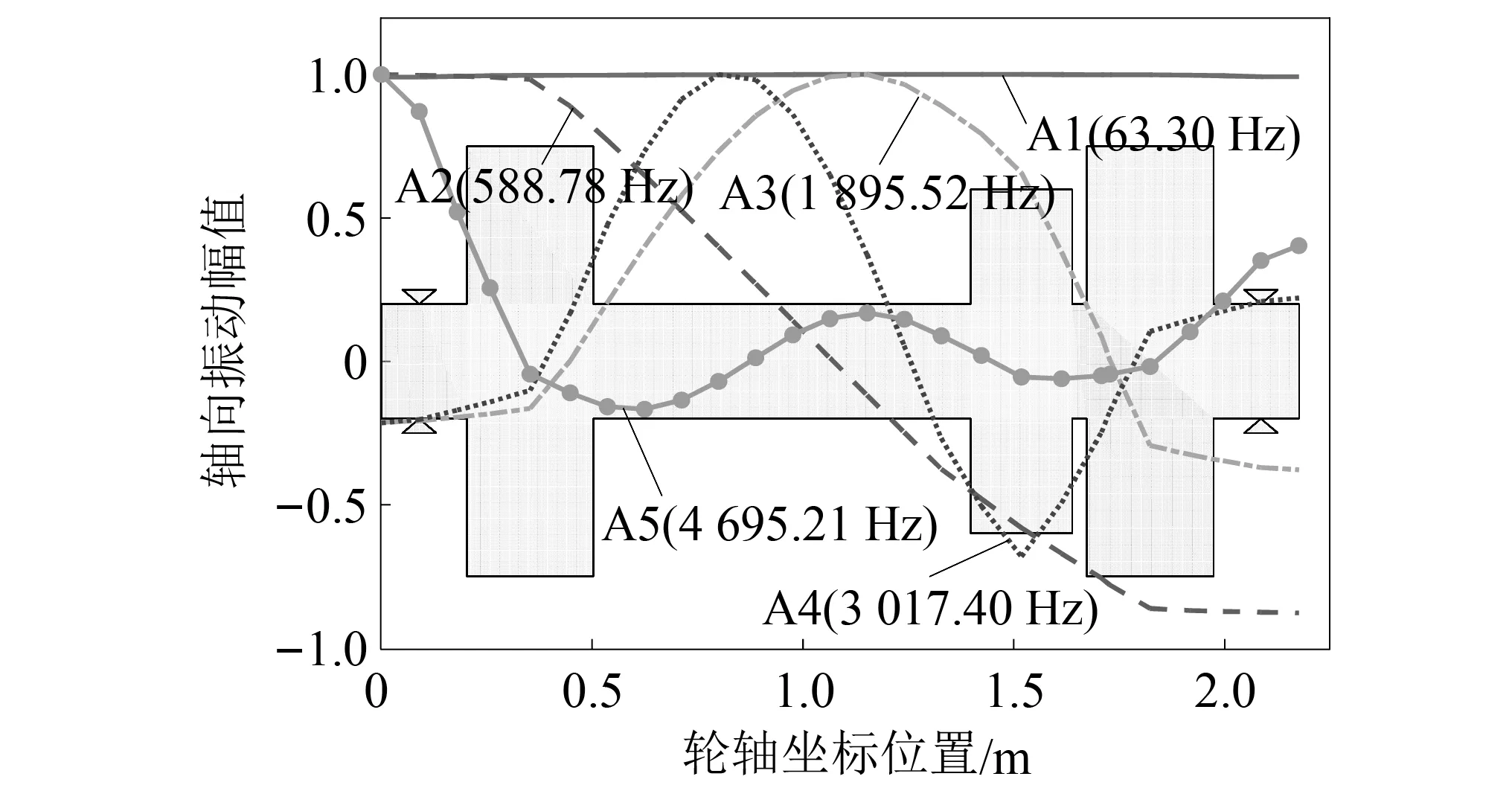
图14 模型4的轴向振型Fig.14 Axial mode shapes of model 4
由扭转振型图13可知,T1在左右车轮两侧的振型较大,车轴中间部位的振型最小,在经过左右车轮节点位置以及大齿轮节点位置时,均出现振型幅值突变的情况(幅值减小或增幅减缓)。扭转振幅突变同样出现在T2,T3,T4及T5,这表明扭振的传递会被具有较大转动惯量的元件(如车轮、大齿轮等)所阻碍,甚至阻断[18]。其中,T2在大齿轮节点处出现最大振幅,而在车轮两侧振幅相对小的多,若该振型被激发则极易引起齿轮啮合不平稳;T3和T4的振动形态则主要被限制在左右车轮之间的车轴部位;T5的扭转振动主要出现在左右车轮的外伸轴段部分,其中右侧车轮的外伸轴段扭振幅度远大于左侧,若该振型被激发则易引起右端轴箱轴承的扭振波动,加剧内、外圈和滚子的接触疲劳,同时也易使得车轴在右车轮处发生扭振疲劳。
由轴向振型图14可知,在具有大质量的车轮和齿轮部位也呈现轴向振动幅值突变的现象,但明显程度略低于扭转振型。其中:A1(63.3 Hz)的振幅波动非常小(实际计算出的最大振幅(4.89×10-4m)及最小幅值(4.85×10-4m)相差也很小),在无量纲化振型图中几近一条直线,表明该振型是动力轮对转子在轴向约束弹性限制下沿轴向作整体运动的振型,因此该振型中的动力轮对可看作刚体;A2(588.78 Hz)的最大振幅位于左右两侧车轮的外侧轴段,整个车轴呈现向两侧的对称拉压运动,该振型下易造成车轮轮缘外侧与钢轨挤压,进而加剧车轮踏面的磨损;A3(1 895.52 Hz)最大振幅位置出现在车轴轴身中心部位;A4(3 017.4 Hz)最大振幅位置出现在轴身中心以及大齿轮等效集中质量部位,在大齿轮处达到最大振幅后出现反转,振幅迅速呈下降趋势,此时轴向大振幅下引起的挤压易使斜齿轮啮合面法向受压迫,加速齿面磨损;A5(4 695.21 Hz)最大振幅位置出现在车轴靠近左车轮的一端,向右出现振幅不规律的波动,整体呈现向右侧的轴向振动。
3.4 轮轨接触点位置对模态结果的影响
考虑到轮轨接触点B的初始位置会因车轮横向运动或钢轨轨底坡等原因而发生变化,如图15所示。本小节以点B到车轮质心平面的距离lBD为参数(图5所示),讨论不同lBD值下动力轮对转子系统振动模态的变化规律。
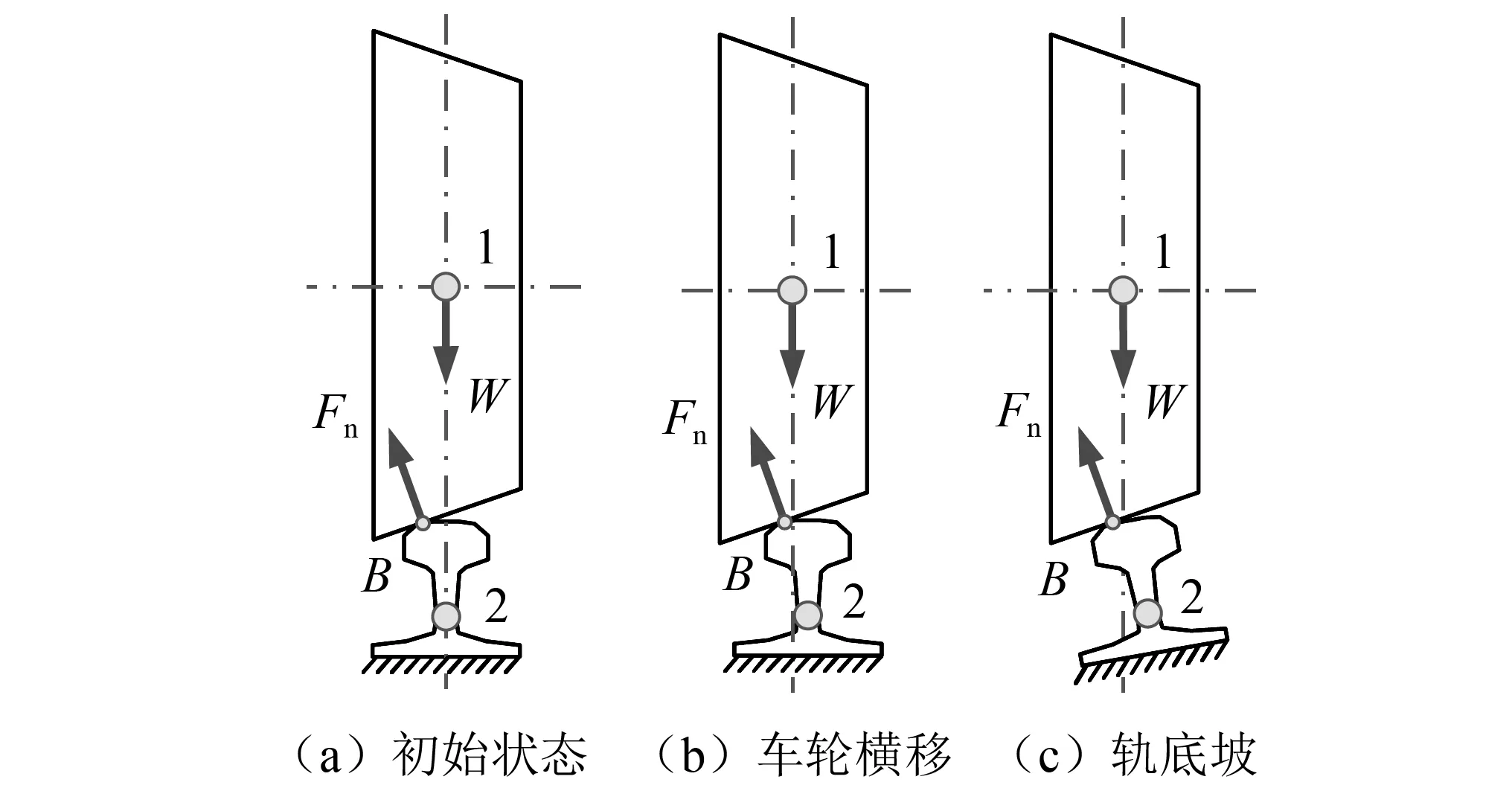
图15 车轮横移或轨底坡引起的轮轨接触位置变化Fig.15 Wheel rail contact position change caused by wheel lateral movement or rail bottom slope
为此,选取lBD∈[0, 0.02]m内的不同值计算系统固有频率,在统计前20阶固有频率变化后,发现随着lBD值的改变,第2~5、第12及第14~20阶模态的固有频率变化均在1 Hz以内,可见较低和较高阶模态固有频率受轮轨接触点位置的改变影响非常有限。相比之下,中间模态(即第6~11及第13阶)的固有频率则受轮轨接触点位置的改变影响更大一些,如表3所示。注:变化中“↑”“↓”分别表示固有频率值上升或下降超过1 Hz,“↗”“↘”分别表示固有频率值上升或下降低于1 Hz,“-”表示固有频率值不变。
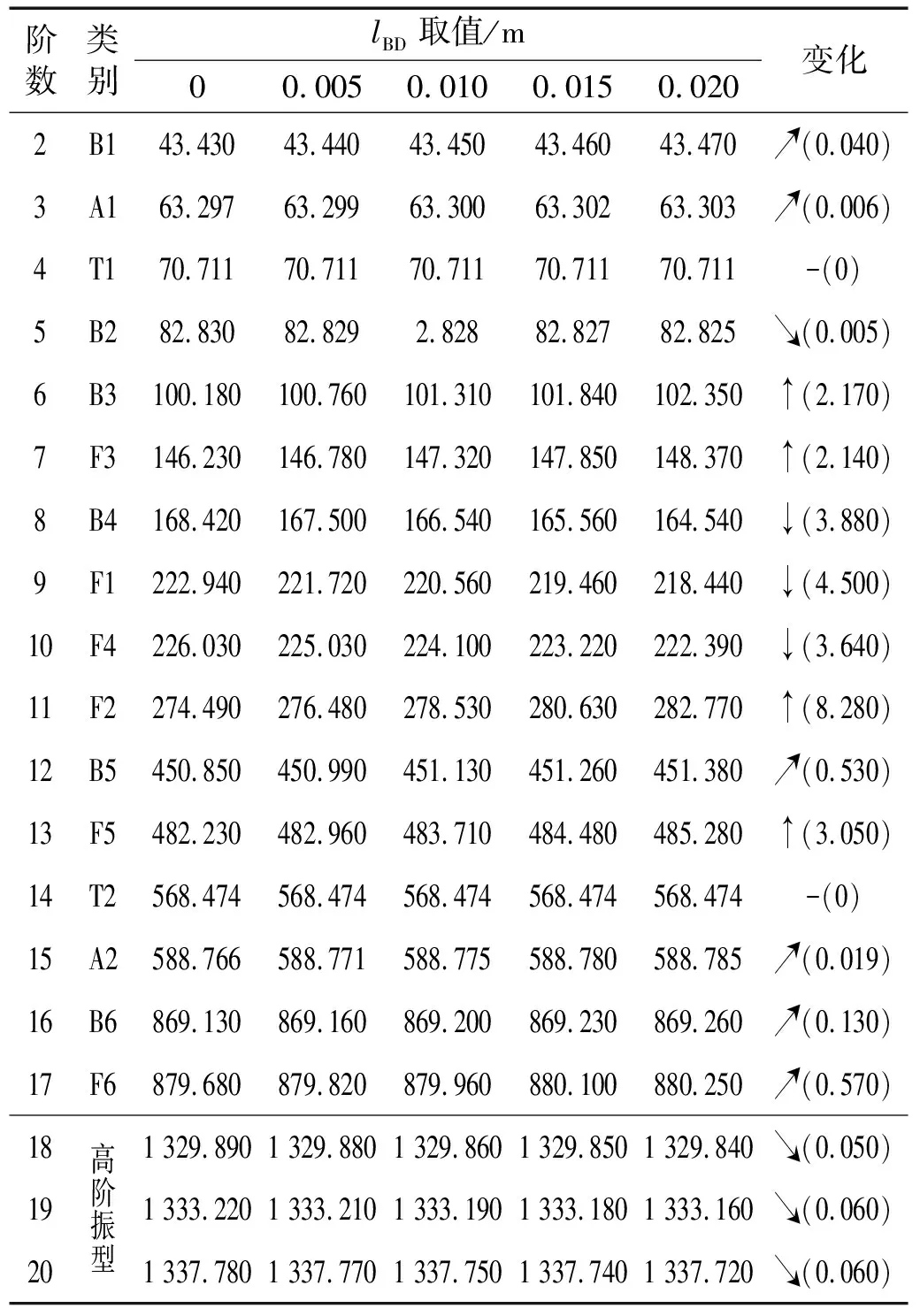
表3 模型4模态频率随lBD值变化情况
由表3可以发现,第6(B3)、第7(F3)、第11(F2)和第13阶(F5)模态的频率随着lBD取值增大而增大;第8(B4)、第9(F1)和第10阶(F4)模态的固有频率随着lBD取值增大而减小。此外,动力轮对的轴向模态频率受lBD的影响较于弯曲模态小很多,而扭转模态频率则完全不受lBD的影响。总体来说,动力轮对转子系统固有频率受轮轨接触点位置的影响较小(模态频率变化最大值仅8.28 Hz)。
4 考虑故障激励的动力轮对共振模态分析
在实际运行中,动力轮对转子系统不断受到轮轨接触、轴箱轴承力、齿轮啮合力、车轮损伤、轨道不平顺等外部复杂激励的持续作用,激励频率不但范围宽,而且异常丰富,特别是存在故障时[19-22]。显然,在复杂的激励频率下,高速运行的柔性动力轮对转子系统极易产生振动稳定性问题,诱发共振模态。
按照振动稳定性设计准则,假设当激励频率处于系统固有频率的5%以内便认为系统存在共振问题。表4列出了前述几种典型故障激励下本算例中动力轮对转子系统可能被激发的共振模态信息。其中,v=400 km/h为列车运行速度;R=0.46 m为车轮半径;f1=93.36 Hz为电机轴转频;f2=38.44 Hz为轮轴转频;fm=3267.6 Hz为齿轮啮合频率(大齿轮数为85,小齿轮数为35);Z=19为轴承滚子数;d=26 mm为滚动体直径;α=10°为轴承接触角;dm=183.93 mm为轴承节径。

表4 典型外部激励下动力轮对转子系统的共振模态
可以看到,在400 km/h的高速列车运行环境下,这些典型激励频率很容易落入动力轮对转子系统的共振频率范围内,特别是车轮损伤故障频率。当考虑轨道不平顺激励时,其短波、中波和长波下的激励频率通过轮轨接触作用传递到轮对系统,则更易诱发系统共振。因此,面对越来越高速的动力轮对转子系统,在全面掌握其弯曲、扭转和轴向振动特性的同时,应注重抗共振模态设计。不过,需要特别注意的是,虽然动力轮对转子系统中与齿轮和轴承相关的故障激励频率存在达到模态共振条件的情形,但考虑到与其相关的故障激励诱发的振动能量通常很小,尤其是诸如齿轮裂纹、轴承保持架等振动能量极小的故障激励,往往是无法诱发相对应的系统共振模态的,最多是加剧轮对系统或零件自身的局部振动,在抗共振模态设计和制定维护策略时应与轮轨故障激励区分对待。
5 结 论
聚焦现有高速列车动力轮对转子系统振动特性的研究不足,在充分考虑轮对的柔性、陀螺效应和约束弹性基础上,推导了一种基于等效圆锥踏面的线性化轮轨接触单元,建立了基于铁木辛柯梁转子有限元理论的动力轮对转子系统方程,详细讨论了轮轨接触弹性和轴箱轴承弹性约束下高速列车动力轮对转子系统的弯曲、轴向和扭转振动特性。主要研究结论如下:
(1) 利用刚度影响系数法和能量法分别推导了轮轨接触单元,且两种方法结果一致;所推导的轮轨接触单元不但适用于圆锥踏面车轮,还可推广至具有真实车轮踏面的场合,仅需根据实际情况获得轮轨接触点位置和接触角即可。
(2) 通过与ANSYS模型结果作对比,验证了自编MATLAB模型程序的正确性;基于自编MATLAB程序设计的四种模态模型中具有全自由度的模型4的模态结果涵盖了其他三种自由度模型的所有频率和振型。
(3) 详细分析了全自由度模型4的弯扭轴模态规律及其与轮对宏观振动特性关系,可以发现——①受轮轨接触刚度的影响,一方面使得反涡动弯曲模态(B1和B2)的涡动轨迹沿纵向呈现严重的扁平状,该振型激发状态下易加剧车轮踏面的磨损;另一方面将正涡动弯曲模态(F1和F2)推迟出现在了更高阶的频率段;②由于推导的轮轨接触单元考虑了垂向和轴向的刚度耦合关系,使得耦合下的轴向和弯曲振动量级接近(见F1和F2),对车辆运行抗倾覆性、蛇形稳定性等性能评估将产生影响;③具有较大等效转动惯量和质量的车轮和齿轮零件使得对应车轴位置处的扭转和轴向振动显著减小;④轮轨接触点位置对动力轮对转子系统的振动特性存在影响,但影响程度较小。
(4) 在典型外部激励下动力轮对转子系统存在共振失稳的可能性,尤以车轮损伤故障激励可能激发的系统模态阶数较多,实际中应开展合理化模态设计。

