内爆炸下单层网壳的破坏模式和泄爆阀值研究

高 伟, 高轩能

(华侨大学 土木工程学院,福建 厦门 361021)

K8型凯威特单层球面网壳由于其造型美观、受力合理,在体育馆、博物馆和商场等公共建筑中得到广泛应用。此类建筑具有人流量大的特点,一旦发生恐怖爆炸袭击和意外爆炸事件,将会造成巨大的人员伤亡和财产损失。因此,对K8型凯威特单层球面网壳在内爆炸下的破坏模式和抗爆性能开展研究,很有必要,也是实际工程防爆抗爆的迫切所需[1]。

李丹等[2]利用杆件轴向应力和塑性应变等指标研究单层网壳结构在箱包炸弹作用下的动力响应,并揭示了该结构在内爆炸下的薄弱位置和形成机理,为网壳结构抗爆设计提供了一定的参考。Qi等[3]结合现场爆炸试验,验证了数值模型的可靠性,并建立一种在外爆炸荷载作用下的结构破坏机制分析方法。徐毅君等[4]采用数值模拟的方法对肋环型网壳的“开口泄爆”展开研究,重点分析连接构件与TNT炸药量的影响,基于超压-冲量准则,提出泄爆阀值的概念。Su等[5-6]研究了爆炸荷载作用下防爆墙对网壳结构的影响,对防爆墙不同高度、不同材料、网壳跨度和炸药量等进行了参数分析,得出了爆炸响应和结构破坏类型等规律。文献[7]以拉格朗日方程为基础,提出了一种理论分析简化模型,可用来计算单层网壳结构在内爆炸作用下的动力响应。Fan等[8]对单层网壳结构在冲击荷载作用下的受力性能展开了数值模拟研究,根据网壳的动力响应总结出了四种失效模式。高轩能等[9-11]运用本征正交分解法将网壳结构表面测点的冲击波超压值分解,得出了大跨空间结构的冲击波超压具体分布,此外,还分析了空间高度、TNT量、结构几何尺寸和炸药位置等因素对网壳结构爆炸响应的影响,提出了大跨结构的泄爆措施。方秦等[12]、李忠献等[13]针对天津港“8·12”特大火灾爆炸事故的结构破坏和毁损情况,分别采用不同方法对爆炸灾害的损毁效应进行了定量评估和数值模拟计算,分析了此次事故中网架等不同类型结构的破坏机理,提出了网架等结构的防爆设计准则。然而,尽管国内外众多学者对爆炸荷载作用下大跨空间结构的性能展开了一定的研究并取得了许多有益的成果,但对内爆炸下空间结构破坏模式和泄爆阀值的研究尚不够深入。

本文应用LS-DYNA通用软件建立K8型凯威特单层球面网壳在内爆炸下的数值计算模型,对网壳结构在内爆炸下的破坏模式和泄爆阀值进行数值模拟计算和定量分析,探讨不同工况下围护结构的破坏类型及其主要影响因素,提出内爆炸作用下,K8型凯威特单层球面网壳的破坏模式分类方法和泄爆阀值计算方法,为该类结构的抗爆和防爆设计提供参考依据。

1 数值计算模型的建立

1.1 结构模型

结构模型为K8型凯威特单层网壳结构,依据JGJ 7—2010《空间网格结构技术规程》[14]进行设计。网壳半径20 m,矢高8 m,矢跨比1/5。网壳杆件为Ф133×11的无缝钢管,下部支撑结构为H形柱,柱高12 m,柱子底部与刚性地面固结,相邻柱子间通过5根工字梁相连,梁和柱的截面尺寸如图1所示。网壳杆件、梁和柱均采用Q235钢。围护结构采用Q235钢板,并通过长度为0.15 m的连接件与主体结构相连。杆件之间以共节点的方式相连。此外,建立尺寸为46 m×46 m×26 m的空气域,使结构模型位于空气域中央。考虑到爆炸冲击波传播特性,将空气的边界设置成无反射边界,并采用球形装药的方式,以模拟炸药的悬空爆炸。建好的有限元模型如图2所示。

图2 有限元模型Fig.2 Finite element model

1.2 单元及材料参数

空气作为一种连续介质,采用3维实体单元Solid164模拟,材料模型为MAT_NULL[15],同时定义空气的状态方程为EOS_LINEAR_POLYNOMIAL,该线性状态方程表达式为

P=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E1

(1)

表1 空气材料参数[16]

炸药同样采用Solid164单元,利用MAT_HIGH_EXPLOSIVE_BURN高爆炸药模型定义炸药的材料参数,并通过JWL状态方程将爆炸冲击波压力定义为

(2)

式中:V为相对体积;A,B,R1,R2、ω为输入参数;E0为初始体积内能;炸药的密度取为1 630 kg/m3,炸药的具体参数如表2所示。

表2 炸药材料参数[17]

爆炸冲击波是一种极强的动力荷载,具有峰值压力大、作用时间短的特点,易对钢结构构件的性能造成不利影响,导致其力学性质发生显著变化,材料强度和失效应变也会提高。故采用MAT_SIMPLIFIED_JOHNSON_COOK(J-C)材料模型来模拟爆炸荷载作用下钢材的本构关系,其表达式为

σ=(A+Bεn)(1+Inε*)

(3)

式中:ε,ε*为等效塑性应变和相对应变率。A,B,n,C为输入参数,利用霍普金森压杆实验对其进行测定,试验结果如表3所示。同时,工字梁、H型柱、网壳杆件以及连接件均采用梁单元Beam161,屋面和墙面采用壳单元Shell163。考虑到冲击波的反射作用,采用MAT_RIGID材料模型定义地面,单元类型为Shell163。

表3 Q235钢J-C模型参数[18]

1.3 任意拉格朗日-欧拉算法

爆炸冲击波在传播过程中,会与各构件和地面产生相互作用。爆炸冲击波可视为流体,各构件和地面视为固体。因此,爆炸过程可采用任意拉格朗日-欧拉 (arbitrary Lagrangian-Eulerian,ALE)算法模拟。该算法是目前处理流固耦合问题的一种常见且有效的有限元计算方法,其结合了拉格朗日(Lagrange)与欧拉(Euler)算法各自的优点,在处理结构边界运动时能有效地追踪物质边界的运动,同时又可以使内部单元网格与实体物质之间相互独立。此外,爆炸冲击波在网壳内部会发生多次反射,使得理论研究与经验公式很难对其进行预测,而ALE算法可以有效地解决这一问题。现有研究表明,采用ALE算法的数值模拟结果与试验结果符合较好[19-20],与理论研究和经验公式相比,ALE算法具有独特的优势。

2 网壳的破坏模式分析

网壳结构在内爆炸下的冲击波传播规律、受力和变形十分复杂。爆炸产生的气态爆轰产物能够在极短的时间内压缩网壳内部空气形成爆炸冲击波,同时释放大量的光和热,随后波阵面会以面荷载的形式作用在网壳的内部结构,冲击波会因此不断地发生反射与绕射,使得冲击波的传播变得更加复杂[21]。此外,网壳内部结构会承受巨大的冲击力,使得结构产生较大塑性变形,严重的话甚至会发生倒塌。在内爆炸作用下,爆炸位置的不确定性,炸药量的变化,结构形式的不同,导致结构的破坏模式也会有一定的差异,防爆方法也会随之改变。为了研究K8型单层球面网壳在内爆炸下的破坏模式,选取网壳不同位置处的典型节点N1、N4、N14、N32、N58、N92、N134、N184作为分析对象。具体位置如图3所示。

图3 特征节点位置Fig.3 Locations of feature nodes

图4为典型节点N1、N4、N14、N32、N58、N92、N134、N184的位移时程曲线。节点位移反映了网壳结构在内爆炸荷载作用下的刚度水平,本文的位移指的是竖直方向的位移。从图中可以看到,0.03 s左右爆炸冲击波抵达网壳附件,节点位移开始增加。由于冲击波会在穹顶附近不断汇聚,使得该位置处的N1、N4节点位移最大,在0.12 s左右达到极大值点,由于围护结构与地面的反射作用,在0.18 s左右引起穹顶附件节点位移出现二次波峰。其余位置的节点最大位移均小于N1、N4,且二次波峰较小或者没有二次波峰。

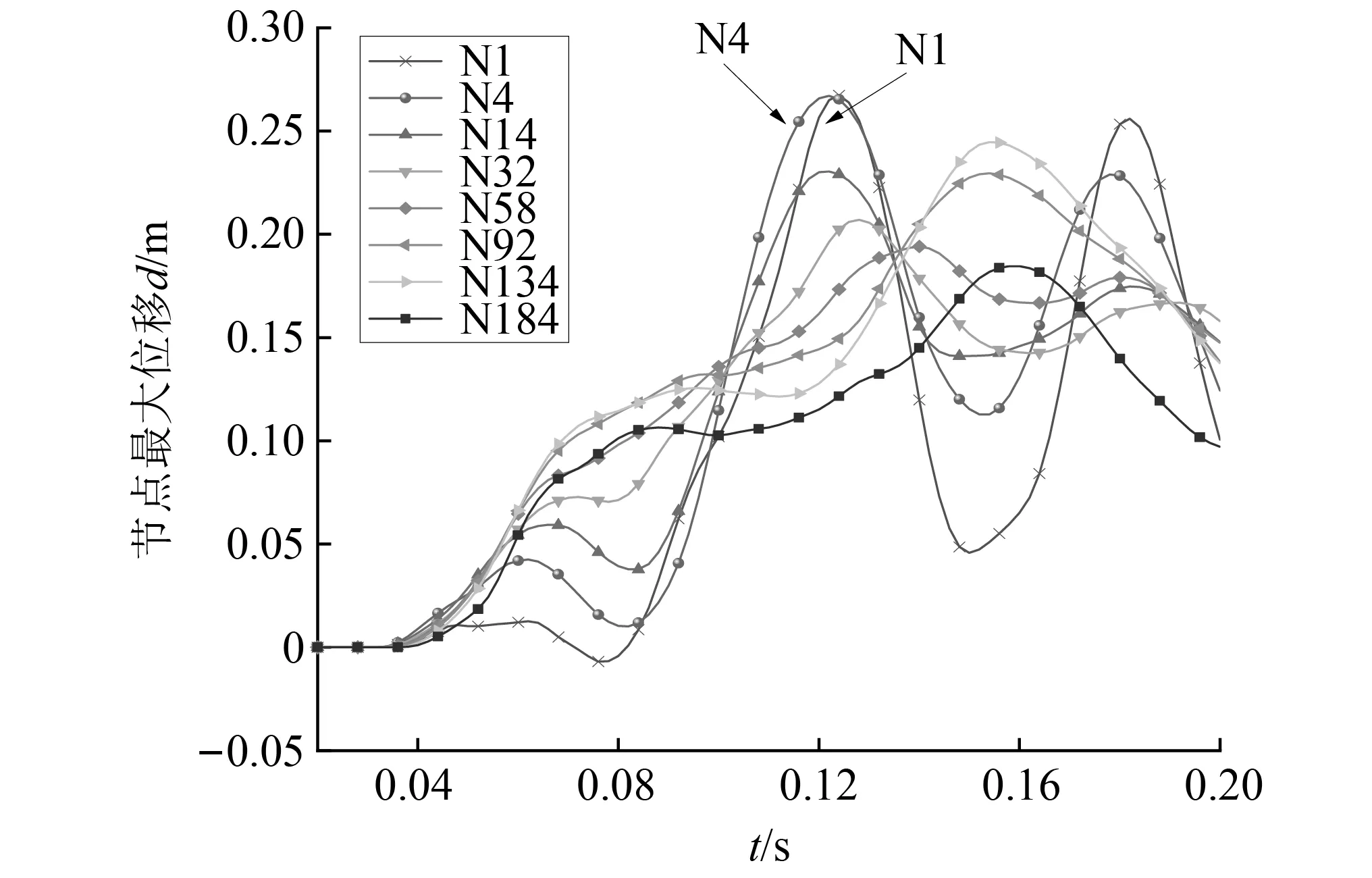
图4 特征节点的竖向位移时程曲线Fig.4 Vertical displacement-time curves of characteristic nodes

2.1 影响破坏模式的因素讨论

2.1.1 爆炸点位置

网壳内部空间尺寸较大,爆炸冲击波会随着距离的增大而不断衰减,当爆炸发生的部位不同时,对结构的破坏模式的影响也是不同的。为了研究爆炸点位置对结构破坏模式的影响,将炸药布置在不同偏心距上。由于网壳为轴对称结构,故仅需考虑一个偏心轴方向即可(本文为y轴方向),炸药与结构中心点的偏心距分别取为0(结构中心),5 m,10 m和15 m。炸药距离地面的高度为1 m。由图4可知,网壳最大节点位移均出现在穹顶附近,为了方便研究,选用节点N1、N4作为特征节点。图5为在不同偏心距下,特征节点N1和N4的位移时程曲线图。如图5所示,当炸药与网壳中心的距离为0时,特征节点N1、N4处的最大位移明显大于其他三种情况,且震荡明显。表明当炸药位置距离结构中心越近,结构的位移响应越大,越不利于结构泄爆。

图5 不同炸药位置的特征节点位移时程曲线Fig.5 Displacement time-history curves of characteristic nodes at different explosive positions

2.1.2 炸药量

冲击波超压与炸药量密切相关,为研究不同炸药量下单层球面网壳的破坏模式,通过改变炸药直径来控制炸药量。如上所述,中心爆炸对结构最不利,故炸药量分别取150 kg,250 kg,350 kg和450 kg。炸药置于网壳结构中心,距离地面高度1 m。同样选取N1、N4作为特征节点讨论。图6为不同炸药量下的N1、N4位移时程曲线图,可以看到,炸药量对结构的破坏模式有较大影响。随着炸药量的增加,节点位移不断增大,结构破坏也越来越严重。由于N1、N4节点位于穹顶附近,会受到反射波的二次作用,且随着炸药量的增大,二次波峰也会随之增大,逐渐超过一次波峰。

图6 不同炸药量下的特征节点位移时程曲线Fig.6 Displacement time-history curves of characteristic nodes under different explosive quantity

2.1.3 连接件刚度

围护结构与主体结构间的连接件刚度,会直接影响结构的泄爆性能。在内爆炸冲击波的作用下,连接件受拉,随着拉力不断增大,连接件达到失效应变而退出工作。最后,会在围护结构表面形成泄爆口。爆炸冲击波从泄爆口泄出,减轻了主体结构的损伤[22]。所以泄爆口形成的关键在于连接件能否达到失效应变,这和连接件的抗拉刚度EA有关(E为材料的弹性模量,本文取206 GPa;A为连接件的截面面积)。为了研究连接件刚度对结构破坏模式的影响,在满足结构正常使用的基础上,分别选取EA为3.64×107N/m,5.24×107N/m,6.47×107N/m,10.1×107N/m,14.6×107N/m,19.8×107N/m和25.9×107N/m进行计算分析。工况为中心爆炸,炸药量150 kg置于离地面高度为1 m处,仍然选用N1、N4节点作为分析对象。

不同连接件刚度下的特征节点位移时程曲线如图7所示。从图7中可以看出,位移时程曲线变化趋势基本相同,当连接件刚度为10.1×107N·m-1时,N1、N4波峰处位移均小于其他几种情况。表明合适的连接件能够减小结构的位移响应,这是因为当连接件刚度较“弱”时,结构整体刚度较小,导致位移响应较大。当连接件刚度较“强”时,虽然结构的整体刚度增加,但结构的泄爆能力也随之减弱,冲击波对杆件的影响增大,位移响应增加。同时结合表4墙面的破坏模式可知,在150 kg炸药的工况下,当连接件刚度为10.1×107N/m时,墙面的破坏模式为B类,这对于结构泄爆是有利的,而随着连接件刚度的增“强”,破坏模式逐渐变为C类,此时不利于结构泄爆,导致位移响应增大。

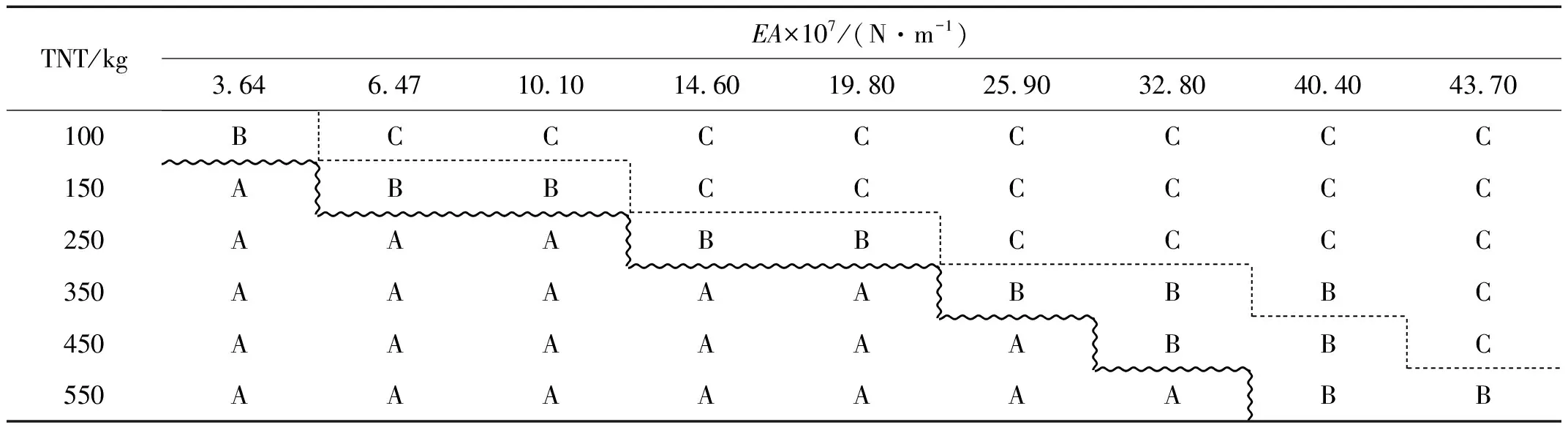
表4 墙面破坏模式汇总

图7 不同连接件刚度下特征节点N1和N4的位移时程曲线Fig.7 Displacement time-history curves of characteristic nodes N1 and N4 with different stiffness of connectors

2.2 围护结构的破坏模式分析

在2.1节中,采用特征节点位移作为响应指标,分析了炸药位置、炸药量以及连接件刚度对网壳结构破坏模式的影响。但由于围护结构受力面积大,承受的爆炸荷载较强,同时现有研究表明,内爆炸下,单层网壳结构的损伤一般先从围护结构开始,所以分析围护结构的破坏模式很有必要。围护结构通过连接件与主体结构相连,连接件刚度成为影响围护结构破坏模式的主要原因。由于中心爆炸对结构泄爆最不利,故本文按中心爆炸讨论不同TNT药量下连接件刚度对围护结构破坏模式的影响。

分别取TNT药量为100 kg,150 kg,250 kg,350 kg,450 kg和550 kg等6个等级,EA分别取为3.64×107N/m,6.47×107N/m, 10.1×107N/m, 14.6×107N/m, 19.8×107N/m, 25.9×107N/m, 32.8×107N/m, 40.4×107N/m和43.7×107N/m等9种不同情况。对K8型凯威特单层球面网壳在内爆炸下的动力响应和破坏模式进行了大量数值仿真计算。经对仿真计算结果进行分析,可以发现,尽管围护结构在不同工况下的破坏模式有所不同,但总体上呈现了一定的规律性。为便于分析比较,可将墙面和屋面的破坏模态分别简化归纳为3种类型。墙面和屋面的典型破坏模态分别如图8和图9所示。

图8 墙面破坏模式Fig.8 Failure modes of wall envelope

图9 屋面破坏模式Fig.9 Failure modes of roof envelope

(1)墙面破坏类型(A、B、C型)。A型:墙面完全脱离主体结构;B型:墙面部分破坏,形成泄爆口;C型:墙面无破损,基本完好。

(2)屋面破坏类型(D、E、F型)。D型:大部分屋面板掀开,形成了大范围的泄爆口;E型:穹顶和外圈屋面板部分掀开,其余部位屋面板基本完好;F型:屋面无破损,基本完好。从图8和图9中可以看出,A型、D型围护结构破坏程度较为严重,墙面与屋面出现较多泄爆口,此时对于结构泄爆非常有利,而B型、E型虽然也有泄爆口,但数量明显比前一类型少,泄爆口也较小,但对于结构泄爆也是有利的,因此,当发生内爆炸时,应尽量控制围护结构发生A型、B型、D型、E型破坏模式。至于C型、F型破坏模式,墙面与屋面基本完好,不利于结构泄爆,应当避免出现此型的破坏模式。

为了更加直观看出不同工况下围护结构破坏模式的变化规律,将不同工况下围护结构的破坏模式汇总在表4和表5中,表中虚线表示破坏模式的分界线。从表4和表5可知,TNT药量较小时,围护结构基本完好,此时泄爆口难以打开。但随着TNT药量的增加,围护结构的破坏程度越来越严重。同时,在TNT药量一定的条件下,随着EA的增大,破坏程度呈现出递减的趋势,不利于结构泄爆,由此可以看出,连接件抗拉刚度对围护结构的破坏模式有较大影响,可通过改变EA的大小来控制结构的破坏模式,从而达到最佳的泄爆效果。

表5 屋面破坏模式汇总

3 网壳结构在内爆炸下的泄爆阀值

3.1 泄爆阀值的提出与定义

围护结构泄爆口的泄爆原理与泄爆阀类同。泄爆阀的工作原理为当系统内部压力大于设计压力时,防爆片自动破碎,压力外泄,从而达到泄压的目的,以防止爆炸事故的发生。本文将这一泄爆原理引入用于大跨钢结构的内爆炸抗爆中,围护结构及连接件共同组成了泄爆阀。结构发生内爆炸时,内部压力迅速增大,当超过设计压力时,连接件断裂,围护结构形成泄爆口,爆炸冲击波从泄爆口泄出,从而达到泄爆效果。本文应用超压-冲量准则,将泄爆阀开启所需的压力值定义为泄爆阀值,也即围护结构破坏所需的冲击波超压值,当冲击波超压大于或等于泄爆阀值时,泄爆阀才开启。

3.2 泄爆阀值的计算

通过ANSYS前处理器找到围护结构表面的空气单元,在LS-PREPOST后处理器中提取相应空气单元的爆炸冲击波压力峰值Pf(单位kPa),压力Pf与标准大气压P0(取100 kPa)的差值为冲击波超压峰值,即泄爆阀值(ΔPf):

ΔPf=Pf-P0

(4)

为使计算的泄爆阀值更加精确,可在围护结构内表面选取多个空气测点,取其平均值作为泄爆阀值。选取的空气单元测点位置如图10所示。墙面选取四个空气单元,86773号空气单元位于柱底端,在该单元正上方4 m,8 m和12 m处再选取另外三个空气单元,其编号依次为154485、222197、281445。屋面选取五个空气单元,其中,416830号空气单元位于屋面穹顶正下方,沿着网壳径向杆件正下方每隔4 m再选取四个空气单元,其编号由高到低依次为408374、391454、366070、332221。计算选取好的空气单元的泄爆阀值,求出墙面和屋面平均泄爆阀值。以TNT炸药为450 kg,连接件抗拉刚度为6.47×107N/m为例,计算该工况下的平均泄爆阀值,此时墙面破坏模式为A型,屋面的破坏模式为D型。

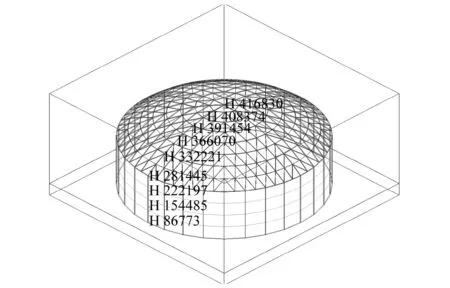
图10 围护结构表面空气单元测点Fig.10 Air elements near envelope structure

图11为围护结构表面选取的空气单元压力随时间变化曲线。由图11(a)墙面空气单元压力曲线可知,86773号空气单元的冲击波压力峰值具有最大值340 kPa,由式(1)可得该空气单元的泄爆阀值为240 kPa,墙面其余三个空气单元泄爆阀值分别为194 kPa,178 kPa和225 kPa。故该工况下墙面所对应的A型破坏模式平均泄爆阀值 。

图11 围护结构表面空气单元压力曲线Fig.11 Pressure curves of air elements on envelope surface

屋面穹顶部位(416830号空气单元)由于冲击波的汇聚现象,会导致二次波峰的出现,且相较于第一次波峰更大,这与Wang等研究中关于网壳结构顶部第二次冲击波超压峰值较大是一致的。但屋面其他部位受汇聚现象影响较小,波峰相较于第一次较小,且结构在第一次波峰作用下结构已经泄爆,故选用第一次超压峰值求泄爆阀值更为合理。则该工况下屋面D型破坏模式的平均泄爆阀值ΔPf=(152+127+100+119+130)/5=126 kPa。

按照相同的方法,计算不同破坏模式下的平均泄爆阀值并汇总在表6和表7中,表中虚线表示对应破坏模式下泄爆阀值的分界线,虚线上方表示泄爆阀值的下限值,下方表示其上限值。例如,在TNT=250 kg,EA=10.1×107N/m工况下,墙面达到A型破坏模式其泄爆阀值上限值为143 kPa,下限值为102 kPa。

表6 墙面破坏模式对应的泄爆阀值

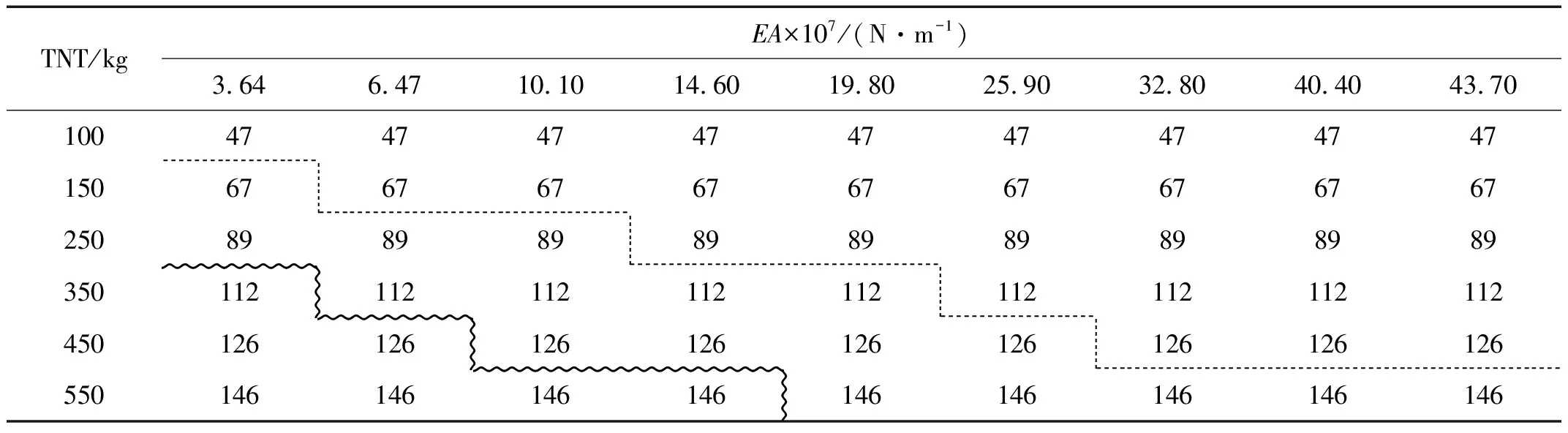
表7 屋面破坏模式对应的泄爆阀值

结合表4与表6可知,墙面破坏模式所对应的泄爆阀值会随着TNT药量的增加而增大。且TNT药量一定时,泄爆阀值相等;但泄爆阀值相等时,其所对应的破坏模式却不一定相同。连接件抗拉刚度一定时,墙面达到的破坏程度越严重所需的泄爆阀值也越大,泄爆阀开启的难度也随之增大。

3.3 泄爆阀值与连接件刚度EA间的关系

根据表6和表7,可以建立为泄爆阀值与EA间的数学关系。由于在墙面中A型破坏模式与B型破坏模式中泄爆阀都易开启,C型泄爆阀难开启,B型与C型是泄爆阀能否打开的分界,故仅需求出B型和C型对应泄爆阀值分界线处的上限值和下限值的平均值。同理屋面也仅对E型与F型的泄爆阀值分界线进行平均处理。将墙面处理后的结果列于表8中,屋面结果列于表9中。为了更加直观看出泄爆阀值与EA之间的关系,通过ORIGIN软件对表8与表9的数据进行拟合,结果如图12与图13所示。曲线上方表示泄爆阀易开启,而下方表示泄爆阀不易开启。

表8 墙面泄爆阀值汇总

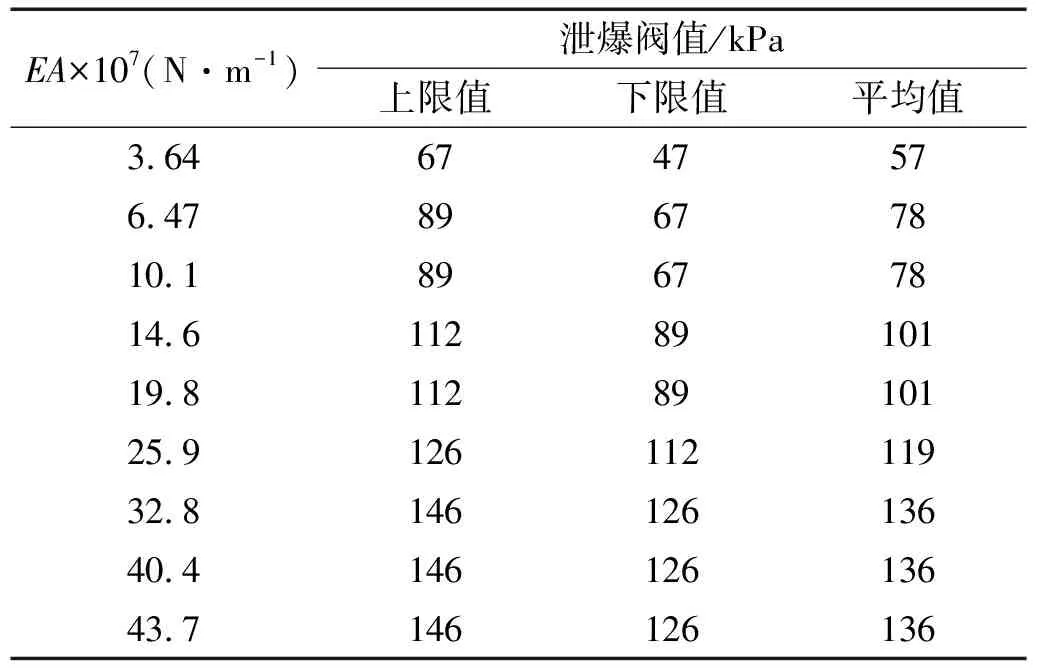
表9 屋面泄爆阀值汇总

图12 墙面泄爆阀值拟合曲线Fig.12 Fitting curve of wall explosion venting threshold

图13 屋面泄爆阀值拟合曲线Fig.13 Fitting curve of roof explosion venting threshold

墙面泄爆阀值与EA的拟合曲线关系式为

(5)

屋面泄爆阀值与EA的拟合曲线关系式为

(6)

从图12和图13中可以看出,曲线拟合程度较高,墙面泄爆阀值随着EA的增大而一直增加,屋面泄爆阀值也随着EA的增大而增加,但最后趋于平稳。由于泄爆阀值是墙面与屋面达到某种破坏模式时所需的超压值,因此,在抗爆设计中,可以通过连接件材料的抗拉刚度EA估算出该结构所能承受的最大冲击波超压值。例如,在图9中,当EA为32.8×107N/m时,由式(5)可估算出墙面的泄爆阀值为166 kPa,表示墙面的冲击波超压值需要最小达到166 kPa时,墙面才破坏,泄爆阀才能开启。

4 结 论

通过采用ANSYS/LS-DYNA建立数值计算模型,对K8型凯威特单层球面网壳在内爆炸下的破坏模式和泄爆阀值进行数值计算和分析,可以得到如下结论。

(1)爆炸点位置、炸药量和连接件刚度等因素对K8型凯威特单层球面网壳在内爆炸下的破坏模式有较大影响。结构中心爆炸时,不利于结构泄爆。网壳穹顶节点位移随炸药量的增加而非线性增大,结构损伤程度加重;合适的连接件刚度可以减小结构的位移响应,有利于结构泄爆。

(2)提出的结构破坏模式划分类型及其判断标准,能够有效地描述K8型凯威特单层球面网壳在内爆炸下的损伤模态,可为结构防爆等级的划分和泄爆设计提供参考依据。

(3)给出了K8型凯威特单层球面网壳在内爆炸下的泄爆阀值计算方法。应用该方法,通过调整围护结构连接件的刚度,可实现围护结构泄爆口的开启,防止主体结构较大损伤和坍塌,可供同类型结构的泄爆计算和抗爆设计提供参考依据。