宽厚比对足尺方钢管混凝土短柱抗震性能影响的试验研究
金 浏, 梁 健, 陈凤娟, 杜修力
(北京工业大学 城市减灾与防灾防护教育部重点实验室,北京 100124)
由于钢管和混凝土之间具有优势互补、协同工作的能力,使钢管混凝土(concrete filled steel tubular,CFST)具有承载力高、延性好的优势,进而被广泛应用在工程结构中[1-3]。在服役期内,钢管混凝土柱不仅承受轴压荷载作用,还可能承受到水平地震作用[4-5]。因此,对钢管混凝土柱抗震性能的研究具有非常重要的意义。
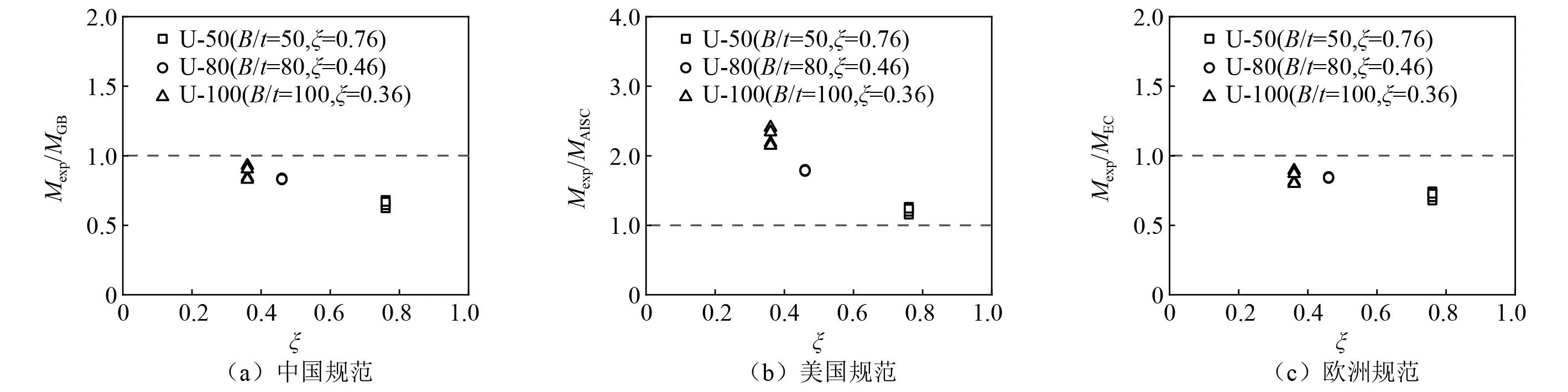
国内外学者[6-9]针对钢管混凝土柱的抗震性能已经开展了较多的研究,并取得了丰硕的成果。这些工作主要聚焦于分析截面形式(圆形、矩形、方形及其他复杂截面)、轴压比、材料(混凝土和钢材)强度、长细比L/B及宽厚比等因素对柱抗震性能的影响规律与机制。研究结果表明:在一定范围内,随着轴压比的增大,钢管混凝土柱的水平承载力呈现上升的趋势;材料强度增大,承载力也表现出上升的趋势;随着长细比的增大,方钢管混凝土柱的水平承载力减小,由强度破坏转变为失稳破坏。在钢管混凝土柱抗震性能试验中,长细比的范围多在3.0~6.0。但是,在建筑结构中,由于层高和轴压比限制的原因,使承重柱的长细比较小,从而形成短柱。在水平力和轴向力作用下,当0.5 近年来,一些研究工作发现结构尺寸增大后,钢管对混凝土的约束作用呈现出下降的趋势,如钢管混凝土柱的轴压[13-14]、偏压[15]以及压剪行为[16]等工作。另外,陈鹏研究表明:现行钢管混凝土柱的规范公式中未考虑尺寸效应的影响;随着截面尺寸的增大,规范会高估大尺寸柱的轴压承载力。因此,对于足尺钢管混凝土柱,钢管对其内部混凝土的约束作用如何,以及其如何影响钢管混凝土柱的抗震性能,是值得研究和讨论的重要问题。 鉴于此,本文以方钢管混凝土短柱(柱有效高度与横截面宽度的比值L/B为2.0)为研究对象,设计并开展了6个足尺方钢管混凝土短柱(横截面宽度B=800 mm)的拟静力加载试验,分析了钢管约束作用(B/t=50,B/t=80,B/t=100)对足尺方钢管混凝土短柱破坏模式、滞回曲线、延性、刚度以及耗能等抗震性能的影响规律。在此基础上,将试验结果与各规范的预测结果进行对比分析,旨在为钢管混凝土结构规范的修订和完善提供试验数据和理论支撑。 本文设计了3组不同宽厚比的钢管混凝土柱,即B/t=50,B/t=80和B/t=100,其对应的钢管约束效应系数ξ分别为0.76,0.46和0.36。本文共设计足尺方钢管混凝土柱6个,每组同宽厚比柱2个,钢管混凝土柱的几何尺寸如图1所示。试件横截面宽度B为800 mm,试件有效高度L均为横截面宽度的2倍,即1 600 mm。钢管壁厚t设计值分别为16 mm,10 mm和8 mm。轴压比n按照n=N(fyAs+fcAc) 确定,N为作用在试件上的轴压力。结合工程实际,本文设计轴压比为0.4。 图1 试件截面及尺寸示意图(mm)Fig.1 Dimensions and configuration of specimens (mm) 足尺方钢管混凝土柱的外部钢管由4块钢板焊接为方钢管,将钢管柱与加劲肋和底部端板进行焊接以保证底座与试件的刚性连接。构件浇筑完成后,将试件上端部用塑料薄膜覆盖,以模拟实际施工后钢管的密闭环境。自然养护28 d后,打磨平整混凝土表面并焊接10 mm厚的顶部端板,保证钢管与混凝土共同受力。 钢板采用Q345钢,按照GB/T 228.1—2010《金属材料 拉伸试验 第1部分:室温试验方法》[18]制作标准拉伸试件并进行其力学性能测试。本次试验所用钢材的力学性能(弹性模量Es、屈服强度fy、抗拉强度fu),如表1所示。 表1 钢材材性表Tab.1 Material properties of steel 所有试件采用同一强度等级的同一批次的商品混凝土进行浇筑。核心混凝土和预留混凝土试块在同条件下进行养护,按照GB/T 50081—2002 《普通混凝土力学性能试验方法》[19]对预留标准立方体(150 mm×150 mm×150 mm)试块进行测试。测得试验时,立方体抗压强度fcu为63.4 MPa。 本试验采用北京工业大学的40 000 kN多功能电液伺服加载系统进行加载,如图2所示。加载时,上部与球铰连接,并通过球铰施加轴力,通过滑板车的水平往复运动对试件施加水平荷载。需要指出的是,球铰中心距离试件上端部的距离约为40~50 mm,对试验结果影响可忽略不计。 注: 1.刚性框架; 2.球较; 3.液压千斤顶;4.试件;5.水平作动器; 6.滑板车。图2 加载装置示意图Fig.2 Schematic diagram of the test device 根据JGJ/T 101—2015《建筑抗震试验规程》[20],首先依据轴压比对试件施加轴向荷载,并在整个加载过程中保持轴力恒定;水平加载采用位移控制的加载方式。根据位移角θ=Δ/L(Δ为水平位移;L为试件有效高度)进行加载控制,先按照每级位移角0.25%进行加载,每级循环1次;当位移角到达1.00%时,增量变为0.5%,每级循环2次,加载制度如图3和表2所示。当试件破坏严重不能承受轴向荷载,或水平荷载下降超过最大值的15%时停止加载,试验结束。 表2 位移角及加载位移幅值Tab.2 Drift ratio and load displacement 图3 加载制度Fig.3 Loading protocol 足尺方钢管混凝土柱测点布置,如图4所示。 图4 测点布置Fig.4 Measuring points arrangement 在加载过程中,通过压力传感器分别对水平和竖向荷载进行测量。在底座处布置水平位移计,测量在水平力作用下试件的水平位移。在方钢管混凝土柱下部范围内,布置横向应变片,以测量钢管的环向应变。 如图5所示,6个足尺方形钢管混凝土短柱的破坏形态大致相似,均产生压弯破坏,即柱底部钢管环状鼓曲、核心混凝土被压碎的行为。由图5可知,钢管的局部屈曲均位于底座上方约100 mm处,这是由于底座的附加约束作用抑制了底部钢管截面的变形。 图5 试件最终破坏形态Fig.5 Failure patterns of all tested columns 所有钢管混凝土柱在恒定轴力和低周往复加载过程中,大致经历了弹性工作阶段、弹塑性工作阶段以及破坏阶段。在弹性工作阶段时,试件无明显现象,钢管外部平整,水平荷载和水平位移近似呈线性关系。随着加载的进行,柱底部钢管屈服,试件进入弹塑性工作阶段,由于在轴压力和水平力的共同作用下,核心混凝土的泊松比逐渐增大,追上或超过钢管的泊松比,核心混凝土膨胀变形使外部钢管受压,外部钢管的环向应变也迅速增大,钢管和混凝土之间的相互作用明显。继续加载,钢管出现局部屈曲,并逐渐由拉压面向腹板面发展,表现出较为显著的鼓曲变形,同时伴随有混凝土被压碎的声音,钢管的环向应变持续增大。之后,钢管鼓曲持续发展并在底部形成环状鼓曲,钢管角部区域出现了漆皮剥落的现象,最终试件水平力降至峰值水平力的85%时,试验结束。 试验结束后,拆除外部钢管可以发现核心混凝土在钢管屈曲范围内被压碎。由图5可知,钢管的鼓曲范围大致为400 mm,在该区域内形成了明显的塑性铰区域,并且贯穿了整个钢管截面。宽厚比对试件的破坏形态影响不明显。 所有试件的水平荷载和水平位移的滞回曲线,如图6所示。在加载初期,试件基本处于弹性,加载和卸载的循环曲线基本重合,残余变形较小,试件耗能较少,刚度退化不明显。随水平加载位移增加,受拉侧钢管屈服,试件进入弹塑性阶段。滞回环包围的面积逐渐增大,耗能能力也不断增强,同时残余变形增大,刚度退化明显。而后,外部钢管在柱底部出现鼓曲,核心混凝土逐渐被压碎,滞回曲线到达峰值点。当水平加载位移进一步增加,水平荷载下降,试件进入下降阶段。外部钢管的鼓曲程度加剧,混凝土被压溃,滞回曲线的斜率降低,残余变形明显增加,刚度退化变缓。各试件的滞回性能大致相同。但试件U-100-1和U-100-2在同级位移下,第2次循环加载时试件的水平荷载明显低于第1次加载,表明宽厚比越大,柱的钢管变形和混凝土累积损伤越快。另外,还可以看出,当到达下降段后,大尺寸方钢管混凝土短柱很快就不能承受竖向和水平荷载而发生破坏,即在荷载-位移曲线的表现为下降段较短。 图6 所有钢管混凝土柱的滞回曲线Fig.6 Hysteretic curves of all tested CFST columns 所有试件的P-Δ骨架曲线如图7所示。由图7可知,随着宽厚比的减小,钢管约束效应提升,方钢管混凝土短柱水平承载力有所提高。结合骨架曲线,采用等效能量法[21-22]计算了骨架曲线的屈服点,以峰值荷载及对应的位移为峰值点。这里,骨架曲线上水平荷载降至峰值点荷载85%时对应的点定义为极限点。各试件特征点的计算结果如表3所示,包括屈服点对应的位移Δy、对应的屈服荷载Py, 峰值点对应的位移Δm、对应的峰值荷载Pm,以及极限点对应的位移Δu、对应的极限荷载Pu。 表3 试件特征点实测值 图7 不同宽厚比试件的骨架曲线Fig.7 Skeleton curves of specimens with different width-to-thickness ratios 当宽厚比由50增至80时(对应的钢管约束作用系数ξ由0.76降低至0.46),本文实测的足尺柱峰值荷载(均值)降低了8.0%,对应的峰值位移(均值)由46.2 mm降低至45.1 mm;当宽厚比由80增至100时(对应的钢管约束作用系数ξ由0.46降低至0.36),本文实测的足尺柱峰值荷载(均值)降低了10.6%,对应的峰值位移(均值)由45.1 mm降低至35.5 mm。随着宽厚比的增大,约束效应降低,足尺方钢管混凝土短柱峰值荷载降低,对应峰值位移逐渐提前。 本文通过位移延性系数μ来描述延性,定义为[23] (1) 本文还采用极限位移转角θ=Δu/L评估足尺方钢管混凝土短柱的变形能力。本试验所有试件的位移延性系数及极限转角,如图8所示。 图8 试件延性性能Fig.8 Ductility performance of specimens 由图8(a)可知,本文所有试件的延性系数基本介于1.86~2.41,与已有试验研究中小尺寸柱的位移延性系数(μ=3.16~6.9)相比,足尺方钢管混凝土短柱的位移延性系数较小(在Dong等的研究中,B=450 mm,L/B=2.1和L/B=3.1,n=0.31和n=0.50;在杜喜凯的研究中,B=250 mm,L/B=2.1,n=0.18~0.51)。这是由于相较于小尺寸柱,大尺寸柱的外部钢管约束效应减弱,核心混凝土的强度和延性的提高有限,使大尺寸柱的延性能力降低。实际上,宽厚比反映了外部钢管对核心混凝土的约束作用,宽厚比大的柱钢管对核心混凝土的约束较弱,宽厚比小的柱钢管对核心混凝土约束较强[24]。但在本文试验中,宽厚比小的足尺方钢管混凝土柱并没有表现更大的位移延性系数。这是因为在加载后期,由于钢管的鼓曲,轴力在钢管和核心混凝土上发生重分布,一部分由钢管承担的轴力转移到核心混凝土上,并且钢管壁厚越大,转移的轴力越多,从而引起核心混凝土的破坏。在已有研究中进行的钢管混凝土柱的低周往复试验也得到了类似结论。 图8(b)为各试件的极限位移转角。由图8(b)可知,足尺方钢管混凝土柱的极限位移转角在0.028~0.035内,能够满足GB 50936—2014《钢管混凝土结构技术规范》中框架结构的层间位移角不小于0.020的限值的要求。此外,宽厚比对柱的极限位移转角的影响不明显。 采用割线刚度K来描述方钢管混凝土柱的刚度退化,其表达式为[25] (2) 式中:Pi为第i级加载的最大荷载; Δi为第i级加载时最大荷载对应的最大位移; “+”和“-”分别为正向加载和负向加载。足尺方钢管混凝土柱刚度退化如图9所示。在加载前期,由于在核心混凝土中不可逆的损伤累积,使刚度衰减较快;随着加载的进行,由于钢管和核心混凝土的塑性发展,以及钢管和核心混凝土之间的约束效应趋于稳定,使试件刚度退化逐渐变缓。同时,宽厚比对足尺方钢管混凝土柱刚度退化曲线的影响不大,不同壁厚的试件刚度退化趋势基本相同。这与小尺寸方钢管混凝土柱试验得到的结论类似。 图9 钢管混凝土柱刚度退化性能Fig.9 Stiffness degradation of the CFST columns 本文采用等效黏滞阻尼系数ξe来衡量结构耗能能力,其表达式为 (3) 式中:SABCD为滞回环的面积;SOBE+ODF为滞回环峰值点对应的三角形面积。足尺方钢管混凝土柱等效黏滞阻尼系数,如图10所示。 图10 试件累积耗能系数Fig.10 Accumulated energy of specimens 由图10可知,等效黏滞阻尼系数随加载圈数的增加而逐渐增大,在加载结束时,试件的等效黏滞阻尼系数处于0.20~0.25。实际上,普通钢筋混凝土柱的等效黏滞阻尼系数的范围通常介于0.15~0.25。总体来说,足尺方钢管混凝土柱具有良好的耗能能力。从图10中可以看出,宽厚比对试件的等效黏滞阻尼系数的影响不显著。已有试验表明,小尺寸柱在破坏时的等效黏滞阻尼系数通常能够达到0.4~0.5。小尺寸柱能够经历较大的塑性变形而水平荷载不明显下降。与小尺寸柱相比,足尺方钢管混凝土短柱的等效黏滞阻尼系数偏小。另外,采用累积耗能E来评估构件耗能能力,如图11所示。随着截面宽厚比的增大,足尺方钢管混凝土柱的累积耗能有所减弱。这是因为当宽厚比减小时,钢管壁厚增大,约束效应增强,核心混凝土能够经历更大的塑性变形;在加载后期,宽厚比较小的试件仍然能够保持较大的塑性变形,从而维持较大的耗能能力。 图11 试件总耗能Fig.11 Total energy of specimens 试验测得的柱拉压面(与加载方向垂直)上的环向应变εh随侧移率的变化曲线,如图12所示。钢管的环向应变能够一定程度地反映钢管对核心混凝土约束效应及其发展规律。 图12 试件环向应变Fig.12 Hoop strain of specimens 在加载前期,钢管环向应变基本呈线性发展;之后,由于核心混凝土的横向变形,钢管和混凝土之间出现相互作用,使应变进一步增大;最终由于钢管鼓曲变形和混凝土变形的加大,钢管对核心混凝土的约束效应减小,核心混凝土破坏,使方钢管混凝土短柱承载力丧失而破坏。由图12可知,钢管环向应变的发展区域大致集中在距底座为300 mm的范围内,并且随着侧移率的增大而增大。主要是由于底部弯矩较大,钢管和核心混凝土的相互作用也主要发生在底部区域,使塑性变形主要集中在柱底部。 另外,由图12可知,随着宽厚比的增大,钢管约束作用系数的减小,足尺钢管混凝土柱环向应变达到屈服时对应的侧移率越小。这是由于:①当宽厚比增大,钢管壁厚减小时,约束效应减弱,内部混凝土膨胀变形致使钢管屈服提前;②当钢管壁厚减小时,承受轴力的钢管易于出现局部屈曲现象。同时,随着宽厚比的增大,钢管壁厚减小,钢管环向应变快速增大,使其约束效应迅速失效,导致承载力降低。 本章主要对比中国规范GB 50936—2014《钢管混凝土结构设计规范》、美国规范ANSI/AISC 360-16及欧洲规范EN 1994-1-1的计算结果与本文足尺钢管混凝土柱试验结果。本文测量了混凝土立方体抗压强度fcu=63.4 MPa,中国规范采用混凝土轴心抗压强度fc=0.64 MPa,fcu=40.6 MPa,美国规范和欧洲规范采用圆柱体抗压强度f′c=0.79 MPa,fcu=47.4 MPa。钢材强度及弹性模量则按照实际测量值(见表1)进行计算。 (1) 中国规范考虑压弯荷载作用时,按照下式进行计算: (4) (5) (6) 式中:βm为等效弯矩系数;Nu和Mu分别为钢管混凝土柱的轴压承载力和受弯承载力;Esc和Asc分别为钢管混凝土构件的弹性模量和截面面积;λ为构件的长细比。 (2) 美国规范按照式(7)计算钢管混凝土柱的压弯承载力: (7) (8) 式中,Nu和Mu分别为钢管混凝土柱的轴压承载力和受弯承载力。 (3) 欧洲规范采用钢筋混凝土构件的计算方法来计算钢管混凝土构件的压弯承载力。假定钢管全截面屈服,基于力和弯矩平衡的理论进行计算。 试验压弯承载力Mexp按照式(9)进行计算 Mexp=PL+NΔm (9) 式中:P和L分别为水平峰值荷载与试件有效高度;N和Δm分别为轴压力和峰值荷载对应的位移。柱附加弯矩与总弯矩的对比结果, 如图13所示。 图13 附加弯矩的比例Fig.13 Proportion of the additional bending moment 由图13可知,附加弯矩的占比在0.12~0.19,随着方钢管混凝土短柱横截面宽度的增大,二阶效应引起的附加弯矩不能够被忽略。中国、美国、欧洲规范计算获得的压弯承载力MGB,MAISC,MEC与本文试验结果Mexp的对比情况,如表4所示。 表4 规范承载力计算值与试验值比较 由表3和表4可知,当宽厚比由50增至100时(对应的钢管约束作用系数ξ由0.76降低至0.36),本文实测的足尺柱平均水平承载力降低了18.0%;而中国、美国、欧洲规范计算所得的承载力则分别降低了38.7%,50.3%,30.7%。无论是各规范计算结果之间的对比,还是规范与试验结果的对比均是存在较大的差异。范重等对直径为600 mm、宽厚比为37.5和50的大尺寸圆钢管混凝土柱开展试验研究,发现其水平承载力也仅相差11.3%。对于这种截面尺寸较大,宽厚比对方形钢管混凝土柱压弯承载力影响明显减弱的行为,可能是由于下述原因造成:①随着截面尺寸的增大,钢管对核心混凝土的约束效应明显减弱,使核心混凝土强度和延性的提高程度在减弱;②由于附加约束的存在,钢管会承受较大的轴向力,而对水平力贡献减少;③当截面尺寸增大时,混凝土强度将显著降低,混凝土贡献部分减小。另外,随着宽厚比的减小,钢管约束效应提升,柱压弯承载力有所提高,但提高的幅度明显小于相关规范值。 由表4和图14可知,本文试验结果比中国规范和欧洲规范的计算结果要小,设计偏于不安全。现有设计规范给出的钢管混凝土构件承载力计算公式多是基于小尺寸钢管混凝土柱试验数据拟合得到,试验试件横截面宽度多介于100~400 mm,尺寸较小。现阶段,针对足尺试件的相关研究较少,现有规范中未考虑结构尺寸带来的影响。这可能是中国规范和欧洲规范的计算结果偏于不安全的原因之一。 图14 试验结果与规范计算结果的对比Fig.14 Comparisons of bearing capacity between experimental and predicted values 由图14(a)可知,随着宽厚比的增大,钢管壁厚减小,约束效应变小时,计算结果趋近于试验结果。在中国规范中采用统一理论并引入约束效应系数来进行钢管混凝土柱承载力计算。当截面尺寸增大时,随着宽厚比的减小,约束效应系数可能被过高地估计而产生较大的计算结果,从而使计算结果偏大。 由表4和图14(b)可知,相比于本文试验结果,美国规范的计算结果偏小。实际上,在美国规范中根据宽厚比的不同将截面分为紧凑截面、非紧凑截面以及细长截面,同时针对不同截面对于混凝土和钢材强度的取值也不同:由紧凑截面到非紧凑截面再到细长截面时,混凝土强度由0.85f′c降低到0.7f′c,钢材强度也从fy降低到fcr(fcr为临界屈曲应力,fcr=9Es/(B/t)2,使方钢管混凝土柱承载力计算结果的安全度一再提高。这应是其计算结果小于本文试验结果的重要原因。由图14(c)可知, 随着宽厚比增大,钢管壁厚减小,约束效应变小时,计算结果也趋近于试验结果。欧洲规范中计算方钢管混凝土柱承载力时认为钢管和混凝土均能到达其强度极限,即屈服强度fy和圆柱体抗压强度f′c。其未考虑在实际工作时,钢管处于双向应力状态(轴向受压和环向受拉),钢管的实际屈服强度要小于其单轴拉压屈服强度[28];同时,混凝土强度随截面尺寸增大而降低,存在一定的尺寸效应。因此,计算足尺方钢管混凝土柱压弯承载力时,钢管和核心混凝土的贡献可能被过高地估计,从而使承载力计算结果偏大;并且当截面宽厚比增大时,钢管可能发生屈曲,而不能充分发挥其强度。 综合中国、美国、欧洲等规范与本文试验结果的对比情况来看,各规范承载力计算公式的科学性和合理性还需进一步讨论和商榷,如:是否考虑尺寸效应带来的影响、是否考虑钢管的双向应力状态以及如何考虑钢管和混凝土的强度取值等。 本文通过6个足尺方钢管混凝土柱的抗震性能试验,分析了钢管约束作用(宽厚比)对其破坏模式以及抗震性能的影响规律,并且针对各规范的压弯承载力预测结果进行了对比分析。得到了如下主要结论: (1) 在往复荷载作用下,本文足尺方钢管混凝土柱的破坏形态与小尺寸试件相似,主要表现为底部钢管环状鼓曲、核心混凝土被压碎的压弯破坏模式;宽厚比对破坏模式的影响不明显。 (2) 相较于小尺寸方钢管混凝土柱,足尺试件的位移延性系数较小,且宽厚比的减少并不明显改善柱的延性能力。与小尺寸柱类似,宽厚比对足尺方钢管混凝土柱的刚度退化趋势和等效黏滞阻尼系数影响不大。但随着宽厚比的增大,试件的总耗能减小。 (3) 在本足尺试验中,宽厚比减小、钢管约束作用系数提高时,水平承载力提高的幅度明显小于相关规范值。本文实测的柱压弯承载力低于中国规范和欧洲规范的计算值,结果偏于不安全;而美国规范计算值则较为保守。 需要说明的是,本文仅研究了宽厚比对足尺试件抗震性能的影响。而对于其他影响因素,如轴压比、材料强度以及长细比等,对足尺方钢管混凝土柱抗震性能的影响有待进一步的研究和讨论。1 试验概况
1.1 试件设计

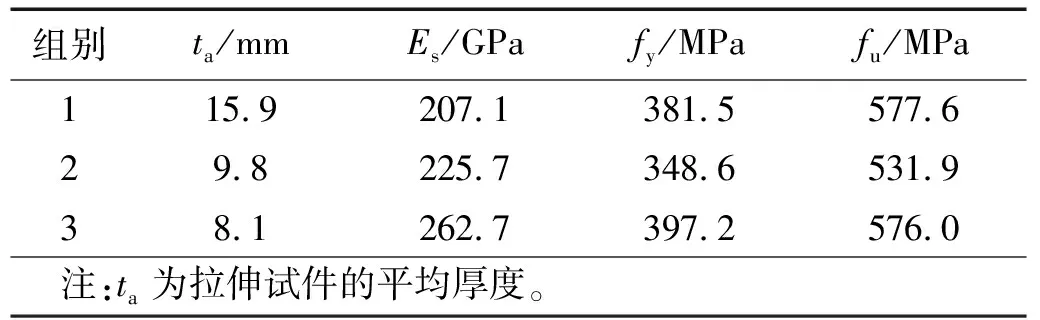
1.2 材料性能
1.3 加载装置与加载制度



1.4 试验测量

2 试验结果与分析
2.1 试验现象及破坏形态

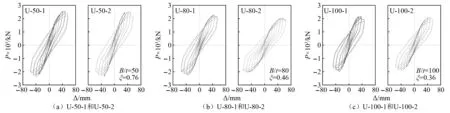
2.2 滞回曲线及骨架曲线


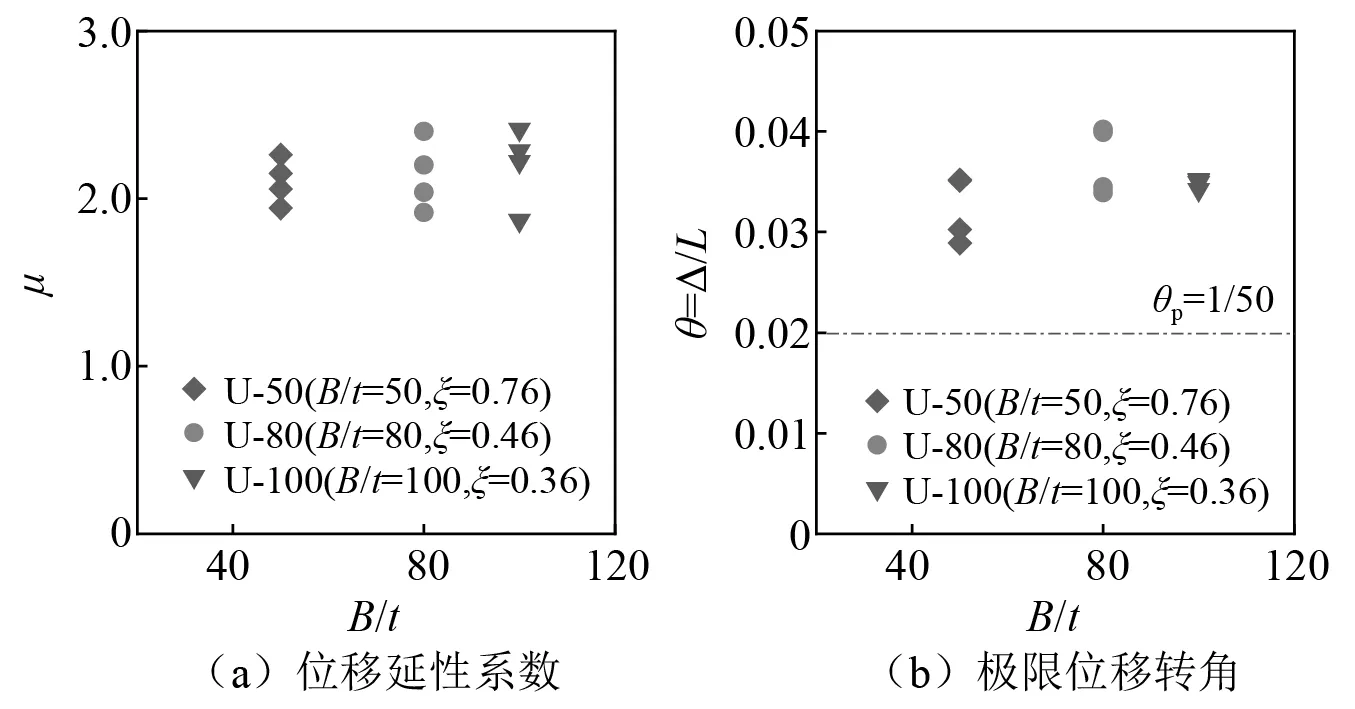
2.3 延性性能
2.4 刚度退化

2.5 耗能能力


2.6 应变分析

3 承载力分析与讨论


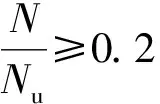



4 结 论

