管道封堵机器人的卡瓦承压性能与管壁损伤特性仿真与试验研究
唐 洋 张吴镝 张玉林 王 远
1.西南石油大学机电工程学院,成都,610500 2.西南石油大学能源装备研究院,成都,610500
0 引言
卡瓦是管道封堵机器人最为重要的核心组成部件之一,其主要作用是降低管道封堵机器人运行速度、支撑管道封堵机器人和固定橡胶筒。现场使用时,卡瓦坐封失效和管壁损伤问题较为突出,已成为当前受关注的焦点问题之一[1-3]。
为了揭示卡瓦减速与坐封失效机理,国内外学者对封隔器卡瓦做了相关研究。仝少凯等[4]利用楔形体应力分析方法分析了RTTS封隔器卡瓦的应力分布及强度。韩传军等[5]以减少卡瓦对套管的损伤为前提,采用滑移线理论、有限元法及与试验相结合的方法,研究了卡瓦坐封过程中的力学行为,计算了卡瓦嵌入套管的深度,优选了结构参数。曹银萍等[6]运用断裂力学理论建立了RTTS封隔器卡瓦处套管二维裂纹与三维裂纹扩展模型,分析了套管二维裂纹和三维裂纹失稳扩展塑性区尺寸。祝效华等[7]基于非线性显式动态分析方法建立有限元模型,综合评估不同卡瓦牙型参数下卡瓦、套管的应力值、等效塑性应变、卡瓦滑移量。王迪等[8]应用有限元法和三维光弹性技术对封隔器卡瓦进行了接触应力分析,介绍了实验模型的建立和实验步骤以及计算模型的建立和边界条件的考虑,比较了数值计算与三维光弹实验的结果,分析了造成误差的原因。王志坚等[9]运用有限元分析软件ANSYS对卡瓦进行有限元数值模拟分析。耿岱等[10]根据他们设计的封堵机器人,利用神经网络建立了卡瓦参数间的函数关系并进行了函数优化,获得最大卡瓦坐封力的结构参数。刘跃宝[11]分析了卡瓦牙齿的几何参数与卡紧效果之间的关系并对其进行了优化。SHAHANI等[12]通过对卡瓦与套管之间简化的接触仿真,得到了卡瓦张开弧度与接触应力间的关系。TANG等[13]基于封隔器卡瓦的承压性能,进行了牙齿参数分析与优选。SUN等[14]采用理论和有限元方法研究了卡瓦与套管之间的相互作用。MACDONALD等[15]通过卡瓦的作用原理对即将产生的损伤进行了计算。上述研究主要涉及油气井中的封隔器卡瓦承压性能和管壁损伤情况分析,也有涉及其结构改进部分。
卡瓦作为防止管道封堵机器人窜动的主要部件,在使用中常出现坐封失效和损伤管壁等问题。然而,管道封堵机器人减速与坐封过程中需考虑卡瓦大尺寸、受力不均匀、受力方向与压缩式封隔器卡瓦不同等因素,因此,井下封隔器卡瓦的研究并不适用于管道封堵作业。同时在研究方法上,目前关于卡瓦的研究并未针对管内减速与坐封过程进行分析,且通过管壁损伤因素分析进而优化卡瓦结构的研究未见报道。本文以降低管壁、卡瓦牙齿损伤情况为前提,采用有限元方法评价卡瓦牙顶角、牙倾角、牙齿数三种参数条件下管道内表面塑性应变和卡瓦塑性应变及Mises应力变化。进一步采用多因素分析方法对卡瓦结构参数进行优化,从而提高卡瓦坐封性能和使用寿命。
1 管道封堵机器人工作机理
1.1 管道封堵机器人工作原理
管道封堵机器人减速坐封过程如图1所示。当管道封堵机器人到达指定位置时,控制封堵模块(图2)上承载的卡瓦和橡胶筒轴向运动,卡瓦随着挤压碗运动径向伸出与管道接触,与管壁产生犁沟效应,将机器人固定在管道内实现坐封。同时,橡胶筒形变膨胀贴合管壁,与管壁产生接触应力。接触应力随着橡胶筒膨胀而增大,最终将管壁与机器人间的环形通道封住[16-17]。

1.调速模块 2.管道 3.封堵模块Ⅰ 4.伸缩模块 5.封堵模块Ⅱ图1 管道封堵机器人坐封过程示意图Fig.1 Setting process of pipeline plugging robot
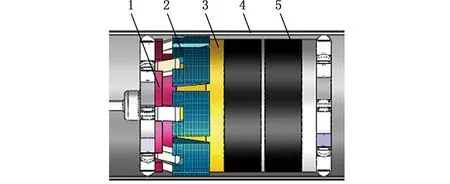
1.挡板 2.卡瓦 3.挤压碗 4.管道 5.橡胶筒图2 封堵模块结构示意图Fig.2 Plugging module structure
1.2 卡瓦坐封过程受力分析
根据油气管道内工况条件,存在10 MPa的介质压差作用在管道封堵机器人橡胶筒一侧的环形截面上时[18-20],管道封堵机器人受到的最大封堵推力
Fp=πpD2/4
(1)
式中,p为管道封堵机器人受到的最大封堵压力,p=10 MPa;D为管道内直径,D=482.6 mm。
卡瓦减速坐封过程中会出现犁沟效应,犁沟效应是指硬金属的粗糙峰嵌入软金属后,在滑动过程中推挤软金属,使之塑性流动并犁出一条沟槽[21],如图3所示。对图3进行受力分析,摩擦力Ff与摩擦因数μ分别为

图3 犁沟效应模型Fig.3 Model of furrow effect
Ff=σsA′=σslh
(2)
(3)
式中,θ为牙顶角,θ=30°;μ为管壁与卡瓦牙齿犁沟效应所得到的摩擦因数,计算得μ=1.866 ;N为管道对卡瓦的正压力;σs为管壁与卡瓦之间的正应力;A为嵌入面面积;A′为侧面面积;l为卡瓦嵌入宽度;h为卡瓦嵌入深度;t为卡瓦嵌入长度。
根据管道封堵机器人卡瓦的减速坐封原理,考虑其坐封过程中的非线性,对模型进行以下简化[22-24]:
(1)由于管道封堵机器人的8个卡瓦呈周向均匀分布,故只分析单个卡瓦。该模型有四个部分:卡瓦、挤压碗、管道和挡板。卡瓦的内表面与挤压碗接触,外表面与套管接触。
(2)设置二维模型进行分析,忽略卡瓦与挤压碗、挡板上的细微特征。
图4中,卡瓦减速坐封过程中,卡瓦在竖直、水平方向上的受力情况分别为

(a)挤压碗
FN1cosγ+FN2sinβ=N+f2cosβ+f1sinγ
(4)
fg+FN2cosβ+f2sinβ=FN1sinγ+f1cosγ
(5)
式中,β为卡瓦与挡板之间的楔形角,β=20°;γ为卡瓦与挤压碗之间的楔形角,γ=20°;FN1为卡瓦与挤压碗之间的正压力;FN2为卡瓦与挡板之间的正压力;f1为卡瓦与挤压碗之间的摩擦力;f2为卡瓦与挡板之间的摩擦力;fg为卡瓦与管道之间的摩擦力。
由摩擦定律得
fg=μN=Fp
(6)
f1=μ1FN1
(7)
f2=μ2FN2
(8)
式中,μ1为卡瓦与挤压碗之间的摩擦因数,μ1=0.15;μ2为卡瓦与支撑盘之间的摩擦因数,μ2=0.15。
挤压碗的受力
FN1=Fhcosγ
(9)
结合式(4)~式(9)得
(10)
式中,Fh为挤压碗推力,计算得出Fh=2120.4 kN。
1.3 管壁损伤因素分析
卡瓦减速坐封过程中,在推力Fh的作用下,卡瓦牙齿逐渐嵌入管道,此过程中接触应力增大,管道和卡瓦会发生弹塑性变形。管壁的损伤情况不仅与正压力Fs有关,还与卡瓦牙齿分布情况有关。由理论可知,推力Fh越大,卡瓦作用管壁的正压力Fs越大,卡瓦与管壁产生的损伤越大[25-26]。由于卡瓦牙齿受力是不均匀的,卡瓦在不同参数情况下所产生的损伤不同,故需研究卡瓦牙齿结构参数,如图5所示,牙齿宽度为b,牙顶角为θ1和θ2,嵌入管道深度为a。
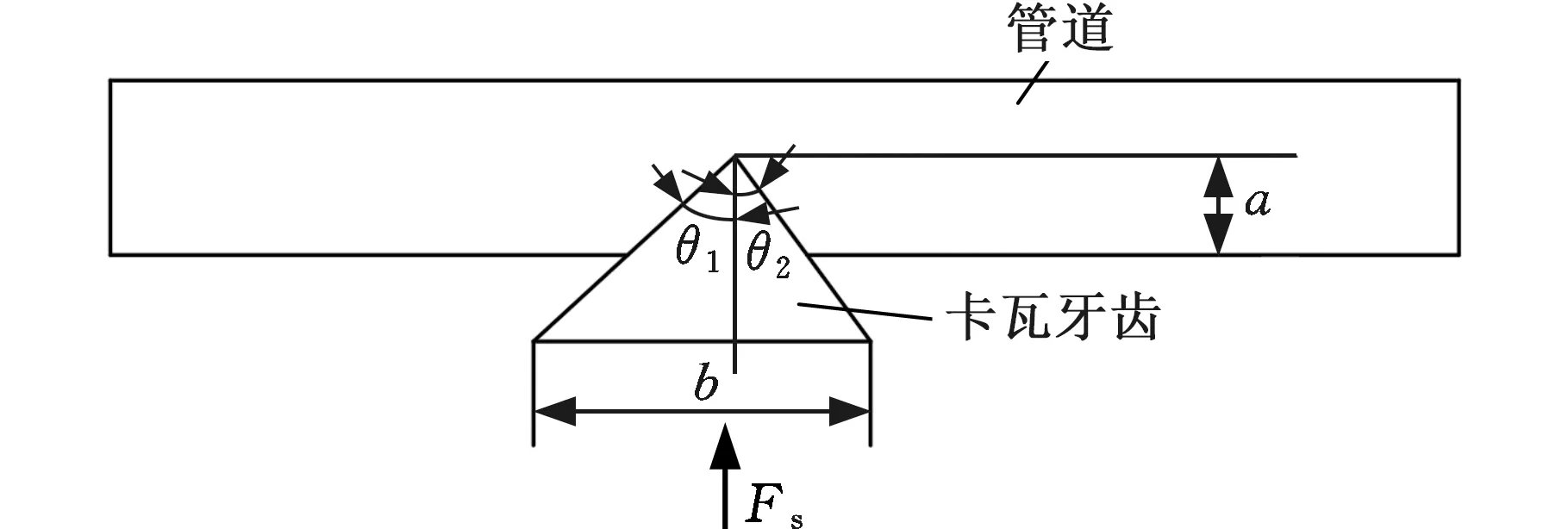
图5 卡瓦坐封时嵌入管壁示意图Fig.5 Schematic diagram of slips embedded in the pipe wall when it is sealed
卡瓦牙齿在正压力Fs作用下向上与管壁接触,产生的挤压力ps为
ps=ψAcaσjy
(11)
Aca=ktpbx
式中,ψ为卡瓦牙齿形状系数,ψ=0.75;k为接触系数;tp为管壁壁厚;bx为牙齿嵌入管壁的宽度;σjy为管道极限挤压强度;Aca为牙齿嵌入面积。
当卡瓦牙齿嵌入管壁深度为a时,牙齿嵌入的宽度bx=a(tanθ1+tanθ2),此时的挤压力
ps=ψktpσjya(tanθ1+tanθ2)
(12)
卡瓦在正压力Fs作用下产生的动能Ek为
Ek=Fs(L+a)
(13)
式中,L为卡瓦运动前与管壁之间的径向距离。
卡瓦牙齿嵌入管壁过程中,管壁对牙齿的阻力做功Ep为
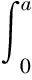
(14)
式中,ps为挤压力。
由能量守恒定律可知
Ek=Ep
(15)
联合式(11)~式(15),解得卡瓦牙齿嵌入管壁的深度
(16)
由上式可知,卡瓦减速坐封过程中牙齿嵌入管壁的深度随着正压力Fs的增大而增加,管壁损伤增大。正压力Fs保持不变,分析不同牙齿结构对管道及卡瓦损伤的影响,选择合理的牙齿技术参数能有效减小管道内表面塑性应变和卡瓦塑性应变及Mises应力。由式(16)可知,卡瓦牙齿的结构参数为:牙顶角θ、牙倾角γ、齿数m(通过改变齿宽b与齿高h来改变齿数m)。
2 管道封堵机器人减速与坐封仿真模型
管道封堵机器人在减速坐封过程中,卡瓦呈周向均匀分布。简化后的仿真模型如图6所示,模型主要包括挤压碗、卡瓦、挡板、管道。
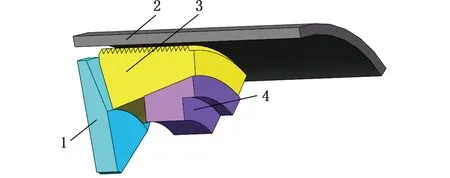
1.挡板 2.管道 3.卡瓦 4.挤压碗图6 卡瓦坐封过程有限元模型Fig.6 Finite element model of slips sealing process
根据现有装置,将卡瓦材料设为20CrMnTi,管道材料根据油气运输管道实际情况设为X65号钢,挤压碗与挡板设为42CrMo,主要材料参数见表1。

表1 各构件与卡瓦材料参数
2.1 卡瓦减速过程仿真模型
分析步选用显式动力学,建立减速动力学模型。此过程设置一条分析步,此分析步中,根据工况减速要求对挤压碗施加轴向载荷39.3 kN,同时给管道施加轴向位移250 mm,约束挡板固定、挤压碗轴向移动自由、卡瓦轴向径向移动双自由,如图7所示。为了保证管壁仿真受力分析准确,在牙齿与整个管壁接触面处布置较为密集的种子。装配体网格划分如图8所示。

图7 卡瓦减速模型载荷及约束设置Fig.7 Load and constraint setting of slip brake model

图8 卡瓦减速模型网格划分Fig.8 Grid division of slip brake model
2.2 卡瓦坐封过程仿真模型
分析步选用显式动力学,为验证卡瓦能否有效坐封住管道封堵机器人,设置两条分析步,第一步为卡瓦的坐封仿真,第二步为验证坐封效果,如图9所示。具体设置如下:在第一条分析步(Step1)中,根据计算的液压缸最小推力要求对挤压碗施加轴向载荷353.4 kN,约束管道与挡板固定、挤压碗轴向移动自由、卡瓦轴向径向移动双自由。第二条分析步(Step2)为管道施加216.9 kN轴向载荷以验证坐封可靠性的仿真分析,在Step1的基础上将管道设置为轴向移动自由。由于该有限元仿真模型有很多硬接触,且形状较为规则,故模型各件均可设为六面体网格,在牙齿与管壁接触面处布置较为密集的种子,装配体网格划分如图10所示。
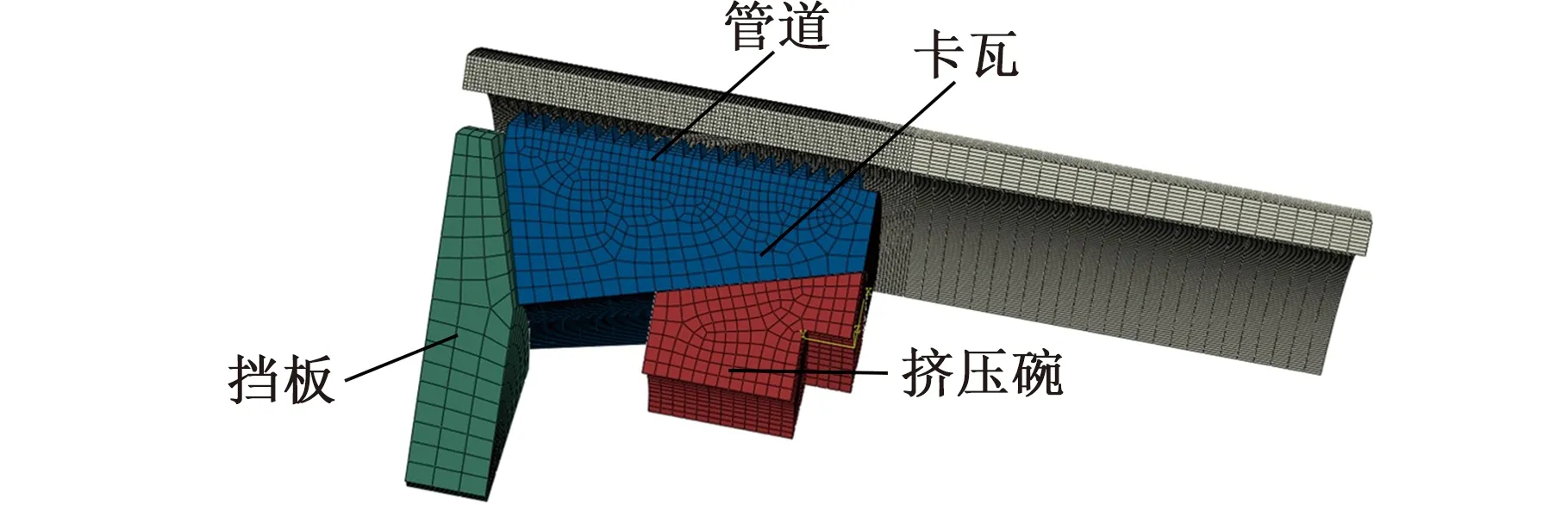
图10 卡瓦坐封有限元模型网格划分Fig.10 Grid division of slip setting finite element model
3 管道封堵机器人减速与坐封仿真分析
3.1 卡瓦牙顶角变化时的减速仿真分析
根据上述分析以及现有工况条件,选择并建立了牙顶角为55°、60°、65°、70°和75°时的卡瓦减速仿真模型。通过管壁上出现的等效塑性应变值来分析不同牙顶角下管壁的损伤情况,如图11所示。

(a)θ=55°
由图11可知,最大等效塑性应变值从大到小依次为牙顶角60°、75°、55°、65°、70°时,主要应变划痕出现在起始接触阶段和即将停止阶段,而中间部分未出现划痕是由于卡瓦接触管壁后收到管壁的作用力而出现一定程度的回调。通过对比分析得出,牙顶角θ=60°时,管壁上应变划痕最明显,应变值最大;而牙顶角θ为65°、70°时,管壁应变值较小,对管壁造成的损伤最小。
同时对减速过程中不同牙顶角参数下卡瓦损伤进行分析,通过仿真得到不同牙顶角参数下卡瓦的最大应力Mises与等效塑性应变值,见表2。由表2可知,随着牙顶角的增大,卡瓦牙齿的最大Mises应力与等效塑性应变整体上逐渐减小,牙顶角θ为70°、75°时,卡瓦牙齿的应力与应变值都很小,对卡瓦造成的损伤较小。
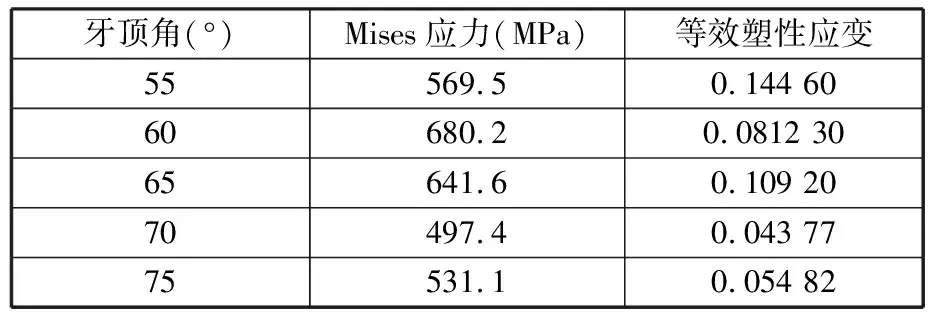
表2 不同牙顶角参数下卡瓦的最大应力Mises与等效塑性应变
结合上述管壁损伤可知,牙顶角θ为55°、60°、75°时,卡瓦或管壁的产生的损伤较大,对比分析后优选牙顶角θ为65°、70°为后续待分析结构。
3.2 卡瓦牙倾角变化时的减速仿真分析
根据减速损伤受力分析研究了不同卡瓦牙齿的牙倾角对管壁及卡瓦的损伤影响,分别建立了牙倾角γ为45°、50°、55°、60°、65°时的减速仿真模型,得到不同牙倾角下管壁的等效塑性应变分布云图(图12)。由图12可知,最大等效塑性应变值从大到小排列为牙倾角45°、55°、65°、60°、50°时,且都只出现在卡瓦刚接触管壁时,各自之间变化幅度较小,而牙倾角γ=45°时,应变值最大且划痕面积最大,管壁所受损伤较大。

(a)γ=45°
对减速过程中不同牙倾角参数下的卡瓦损伤进行分析,通过仿真得到不同牙倾角参数下卡瓦的最大应力Mises与等效塑性应变值,见表3。

表3 不同牙倾角参数下卡瓦的最大应力Mises与等效塑性应变
由表3可以得出,随着牙倾角的增加,卡瓦牙齿的最大Mises应力与等效塑性应变逐渐减小,但当牙倾角γ为65°时,卡瓦牙齿等效塑性应变突然增大,说明牙倾角过大会加重牙齿在减速阶段时的磨损。当γ为55°、60°时,卡瓦牙齿的应力应变值较小,对卡瓦造成的损伤较小。
结合上述管壁损伤可知,γ为45°、50°、65°时,卡瓦或管壁的产生的损伤较大,对比分析后优选牙倾角γ为55°、60°为后续待分析结构。
3.3 卡瓦牙齿数变化时的减速仿真分析
根据实际工程的卡瓦齿数参数条件,选取卡瓦牙齿数m为12、14、16、18、20时的卡瓦参数并建立了减速仿真的有限元模型,得到不同牙齿数下管壁的等效塑性应变分布云图(图13)。

(a)m=12
由图13可知,最大等效塑性应变值从大到小排列为牙齿数m为14、12、16、20、18时。与牙顶角、牙倾角参数的影响相比,牙齿数变化时管道等效塑性应变的变化很小,由此可知,卡瓦齿数变化对减速阶段管壁损伤的影响较小,且对管壁的损伤都很小,则该5种齿数均可选择。
对减速过程不同牙齿数参数下的卡瓦损伤进行分析,通过仿真得到不同牙齿数参数下卡瓦的最大应力Mises与等效塑性应变值,见表4。可知,m=14时卡瓦最大Mises应力最大,m=16时等效塑性应变最大,而m为18、20时卡瓦牙齿的应力应变值相对较小,对卡瓦造成的损伤较小。
结合上述管壁损伤分析可知,当卡瓦齿数m为18、20时,卡瓦与管壁的损伤最小,优选为后续待分析结构。综上分析,管道封堵机器人在减速阶段,卡瓦牙顶角与牙倾角对管壁的损伤影响较大,牙齿数的影响较小,且当卡瓦牙顶角θ=70°、牙倾角γ=60°、齿数m为18、20时,减速阶段卡瓦与管壁的损伤最小。
3.4 卡瓦牙顶角变化时的坐封仿真分析
与减速阶段牙顶角参数相同,选取牙顶角55°、60°、65°、70°和75°的卡瓦牙齿结构进行坐封仿真分析,以及不同牙顶角参数下管壁与卡瓦的坐封阶段损伤分析,得到管壁的Mises应力与等效塑性应变分布,如图14所示。
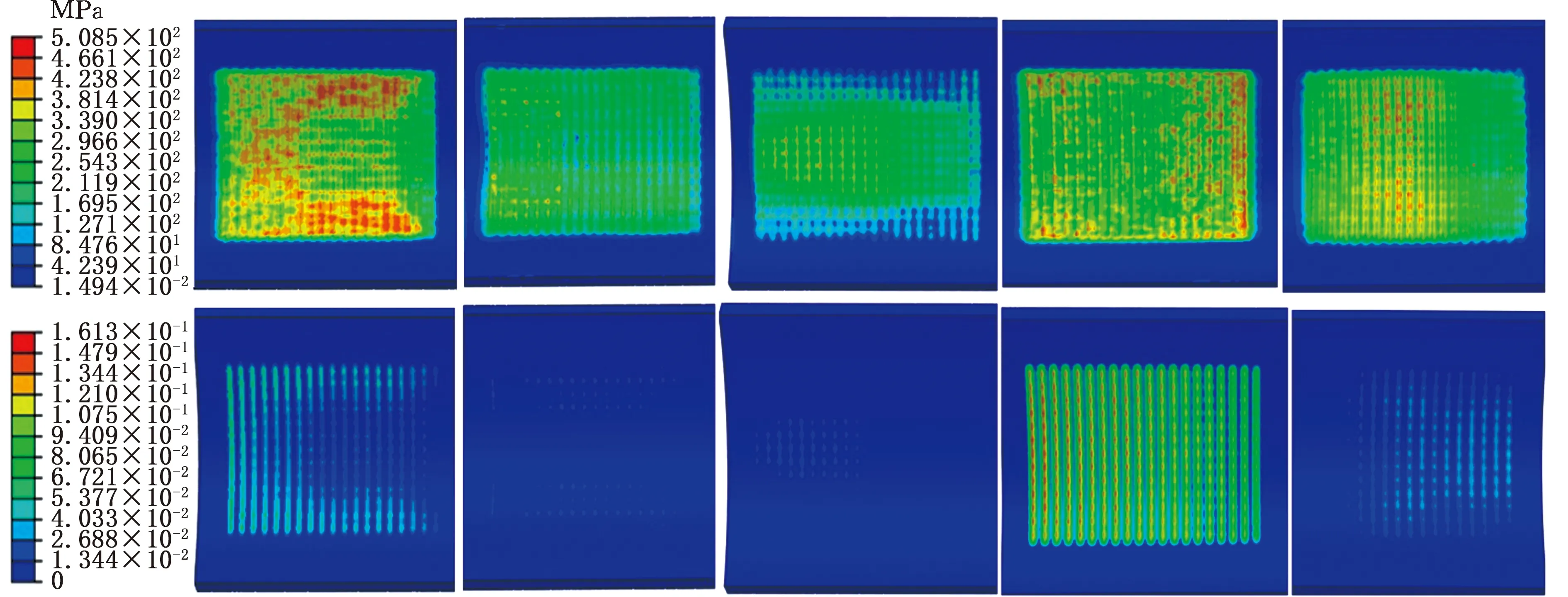
θ=55° θ=60° θ=65° θ=70° θ=75°图14 卡瓦牙顶角变化时坐封阶段管道Mises应力(上)与等效塑性应变(下)分布情况Fig.14 Distribution of the Mises stress (top) and equivalent plastic strain (bottom) in the setting stage when the lip angle changes
由图14可知,管道在卡瓦牙齿作用下应力应变较大,牙顶角θ为55°、70°、75°时Mises应力集中现象明显,且等效塑性应变较大,尤其θ=55°时Mises应力分布最明显,θ=70°时等效塑性应变分布的值最大,而θ为60°、65°时Mises应力与等效塑性应变均较小,说明θ为55°、70°时管壁损伤较大,θ为60°、65°时管壁损伤较小。
同时进行坐封过程中的卡瓦损伤分析,仿真得到卡瓦牙齿在不同牙顶角参数下的应力应变分布情况,如图15所示。可以看出,在卡瓦坐封阶段,随卡瓦牙顶角变化,Mises应力与等效塑性应变的变化幅度较小。牙顶角θ=60°时卡瓦牙齿的等效塑性应变最大;θ=75°时卡瓦牙齿的Mises应力分布面积最大,对卡瓦的损伤最大。
综合管壁与卡瓦的损伤应力应变分析可得,牙顶角θ为55°、70°时管壁所受损伤最大;θ为60°、75°时卡瓦齿面损伤最大,对比分析后优选θ=65°为后续待分析结构。
3.5 卡瓦牙倾角变化时的坐封仿真分析
根据建立的牙倾角γ为45°、50°、55°、60°、65°时的坐封仿真模型,进行不同牙倾角参数下管壁与卡瓦的坐封阶段损伤分析,得到管壁的Mises应力与等效塑性应变分布,如图16所示。可以看出,卡瓦牙倾角γ变化时管壁的Mises应力与等效塑性应变没有明显变化;γ为55°、60°时,管壁的应力应变值相对较小。
同时也得到了卡瓦齿面在牙倾角γ变化时的应力应变分布情况,如图17所示。可以看出,牙倾角γ为45°、50°、65°时,卡瓦齿面出现应力集中,且等效塑性应变较大,即齿面损伤较大。而γ为55°、60°时,齿面应力应变均很小,表明该结构对齿面的损伤很小。
综合管壁与卡瓦的损伤应力应变分析可得,牙倾角γ为45°、50°、65°时,卡瓦齿面损伤最大。对比分析后优选γ为55°、60°为后续待分析结构。
3.6 卡瓦牙齿数变化时的坐封仿真分析
根据建立的牙齿数m为12、14、16、18、20时的坐封仿真模型,进行不同牙齿数参数下管壁与卡瓦的坐封阶段损伤分析,得到管壁的Mises应力与等效塑性应变分布,如图18所示。可以看出,m=20时,管壁的Mises应力最大且等效塑性应变分布面积最广,管壁损伤最大。m为12、18时,管壁应力、应变值及分布都相对较小,表明其所受损伤最小。

m=12 m=14 m=16 m=18 m=20图18 卡瓦牙齿数变化时管道Mises应力(上)与等效塑性应变(下)分布情况Fig.18 Distribution of Mises stress (top) and equivalent plastic strain (bottom) when the number of slips m changed
仿真得到卡瓦牙齿数m变化时的应力应变分布情况,如图19所示。可以看出,m=14时,齿面Mises应力最大;m=16时,齿面上等效塑性应变最大。由此可知,m为14、16时卡瓦齿面损伤最大。m=20时,齿面应力应变最小,其所受损伤最小。
3.7 卡瓦的结构优选及性能验证
由上述仿真分析可知,减速阶段卡瓦所受的损伤较小,因此减速阶段分析管壁的摩擦损伤即可,坐封阶段需综合考虑管壁及卡瓦齿面的损伤。在卡瓦坐封管壁损伤机理分析及其结构参数优化过程中,管壁的损伤情况是最值得关注的,然后考虑卡瓦自身损伤情况。
在减速阶段,θ=60°、γ=45°、m=14时,管壁的损伤最大。在坐封阶段,θ为55°、70°,m=20时,管壁的损伤最大;当θ为60°、75°,γ为45°、50°、65°,m=16时,卡瓦齿面的损伤较大,以上技术参数组合不适合作为管道封堵机器人卡瓦牙齿结构参数。因此,θ=65°,γ=55°、60°,m=12、18为卡瓦牙齿的相对较优的技术参数组合,重新将这三类参数组合优化(表5),再一次进行卡瓦的减速与坐封仿真分析,以求得最优的卡瓦结构。
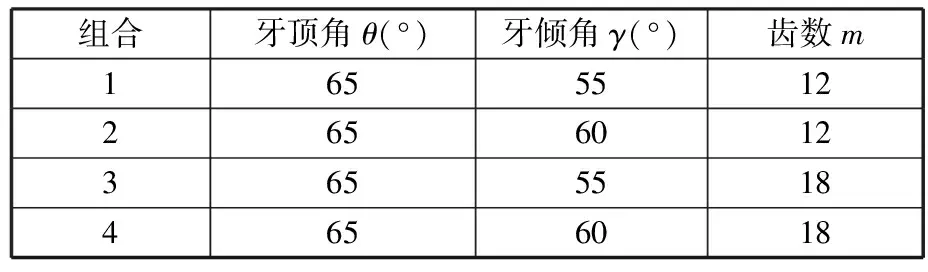
表5 卡瓦牙齿结构参数优化组合
由上述分析可知,减速阶段卡瓦所受的损伤较小,因此减速阶段仅分析管壁的摩擦损伤即可。优化后的仿真结果如图20~图22所示。

(a)组合1

组合1 组合2 组合3 组合4图21 不同组合参数下卡瓦坐封阶段管壁的Mises应力(上)与等效塑性应变(下)分布Fig.21 Distribution of Mises stress (top) and equivalent plastic strain (bottom) of the wall of slips sealing stage under different combination parameters
由上述仿真云图可以看出,管壁与卡瓦齿面产生的应力、应变均减小,分布更加均匀,管壁及卡瓦齿面损伤有所减小。减速阶段组合1与组合4管壁的损伤最小。坐封阶段组合2与组合4管壁损伤最小,组合3与组合4的卡瓦损伤最小。综上所述可得:卡瓦结构为组合4时,管道封堵机器人坐封管道时对管壁的损伤最小,并且卡瓦自身损伤也是最小。因此,在满足工况的条件下,卡瓦牙齿的最优结构为:牙顶角θ=65°,牙倾角γ=60°,齿数m=18。
最后选取θ=65°、γ=60°、m=18的最优卡瓦结构进行坐封仿真验证。设置两条分析步:第一条分析步(Step1)为卡瓦坐封分析,根据管道封堵机器人中最小推力要求对挤压碗施加轴向载荷353.4 kN,约束管道与挡板固定,挤压碗轴向移动自由,卡瓦轴向径向移动双自由;第二条分析步(Step2)为根据工况对管道轴向施加216.9 kN载荷,以验证坐封可靠性,在Step1的基础上将管道设置为轴向移动自由。Step2结束后的仿真结果位移云图见图23,可知管道在卡瓦满足工况的受载荷条件换算下,管道的位移量为0,未出现滑移现象,说明上述优选出的卡瓦结构能满足坐封的可靠性要求。

1.挡板 2.管道 3.卡瓦 4.挤压碗图23 卡瓦坐封及验证阶段各部件的位移云图Fig.23 Displacement nephogram of each component in slips setting and verification stage
4 卡瓦承压性能与管壁损伤特性实验
4.1 实验方案设计
卡瓦材质坚硬,会对油气管道造成一定程度的损伤,分为摩擦损伤与坐封损伤。坐封损伤面积小,受损程度主要与坐封力有关,摩擦损伤的面积大,管道受损情况与卡瓦结构密切相关。因此,本文进行卡瓦与管道间摩擦损伤的实验分析,根据仿真选择的4组正交组合完成减速与坐封模拟实验,进行结果对比分析,主要实验方案如图24所示。

1.下夹板 2.上夹板 3.卡瓦试件 4.施力螺栓5.管道试件 6.夹持块图24 卡瓦与管壁减速与坐封模拟实验方案Fig.24 Friction test scheme of slips and pipeline wall
先通过夹板将管道与卡瓦试件固定,在夹板上通过施力螺栓施加卡瓦与管道之间的正压力,通过力矩扳手确定施加载荷。之后在伸缩液压机的拉力下,使卡瓦与管道试件之间产生相对滑移。最后通过观察与扫描管道上出现的划痕进行分析判断,并与仿真结果进行对比,得到最优的卡瓦牙型实验结构。
由管道封堵机器人卡瓦减速仿真所施加的作用力为39.3 kN及式(10)可得,实验中通过力矩扳手所施加的螺栓预紧力F0=164.2 kN。拧紧力矩T等于螺旋副间的摩擦阻力矩T1和螺母环形端面与被连接件支承面间的摩擦阻力矩T2之和,即
T=T1+T2
(17)
螺旋副间的摩擦力矩
(18)
式中,φ为螺纹升角;φv为螺旋副的当量摩擦角;d2为螺纹中径,d2=0.9d。
螺母与支承面间摩擦阻力矩
(19)
式中,f为摩擦因数,无润滑时f取值范围为0.1~0.2;d0为螺栓孔径;D0为螺母环形支承面的外径。
将式(18)、式(19)代入式(17),得
(20)
其中,fc为螺母与支承面间的摩擦因数。对于本实验装置中M16粗牙普通螺纹的钢制螺栓,φ取值范围为1°42′~3°2′,φv=arctan 1.155f,d0≈1.1d,D0≈1.5d,fc=0.15[27]。d为螺栓公称直径,d=16 mm。将上述参数代入式(20),整理得
T≈0.2F0d
(21)
计算出所需力矩T=105 N·m。
4.2 试验测试与结果
卡瓦试件根据仿真选择的4组正交组合进行实验,各组合参数见表5。将试验装置组装完成,如图25所示。

图25 卡瓦试验装置组装图Fig.25 Assembly diagram of the slips test device
(1)主要试验装置。①拉压试验机。ETM系列电子万能试验机,最大载荷可达10 t。②显微镜。显微镜可以更加直观方便地观察并记录管壁磨损严重点处情况。
(2)试验步骤。①将卡瓦试件与管道试件之间通过上下夹具固定,力矩扳手设定为105 N·m,并将各螺栓拧至预设扭矩值。②将组装好的试件装入试验机上,如图26所示。③开启拉伸试验机,设置试验机的拉伸参数,行进位移为50 mm。④关闭试验机,取下试验后试件,重新装夹下一组卡瓦试件,重复前三个步骤,共四组。⑤将试验后的四组管壁接触面通过显微镜对损伤最大点处放大观察对比并记录。实验流程如图27所示。

图26 试验机组装图Fig.26 Assembly of testing machine

图27 实验流程图Fig.27 Experimental procedure
(3)试验结果与分析。得到的管道试件试验结果如图28所示,可以看出,组合2与组合3下管壁磨损程度最大,划痕深度大且面积广,管壁损伤较为严重。组合4管壁的磨损最小,划痕的深度最小且面积较小,与之前仿真所得结论相对应,对仿真结果进行验证,进一步得到卡瓦牙齿的最优结构参数组合为:牙顶角θ=65°,牙倾角γ=60°,齿数m=18。

图28 不同卡瓦组合的管壁磨损情况Fig.28 Pipeline wall wear under different slips combinations
5 结论
为了确保卡瓦能起到良好固定管道封堵机器人的作用,同时减少对管道的损伤,本文以降低管道管壁、卡瓦牙齿损伤情况为前提,进行了管道封堵机器人减速坐封过程受力分析和管壁损伤因素分析,建立了卡瓦坐封机理的有限元仿真模型。通过正交试验法对卡瓦结构的设计参数进行了优化,建立了可见的室内试验并对仿真模型进行验证。得出的结论如下:
(1)管道封堵机器人坐封过程中,卡瓦作用管壁的Mises应力与等效塑性应变在轴向与径向上分布不均。且随着不同参数的变化,管壁的Mises应力与等效塑性应变未出现明显的规律性变化。各技术参数条件下卡瓦均满足坐封要求,未出现卡瓦滑移现象。
(2)合理的优化卡瓦结构参数可以有效提高卡瓦工作寿命减小管道损伤,以提高管道封堵机器人的工作性能。牙顶角θ=65°,牙倾角γ为55°、60°,齿数m为12、18时,管壁与卡瓦所产生的损伤均相对较小。
(3)根据卡瓦的有限元仿真结果加工出4种卡瓦进行减速与坐封单元试验。试验结果表明,4种卡瓦分别在所对应的载荷下均满足坐封要求,分析管壁的磨损及划痕的深度,并与之前仿真所得结论相对应,对仿真结果进行验证,进一步得出卡瓦牙齿的最优结构参数组合为:牙顶角θ=65°,牙倾角γ=60°,齿数m=18。
(4)本文研究结果对开发高性能、高寿命、高可靠性管道封堵机器人具有重要的参考意义。

