多轨道数字音频自适应变阶谱降噪模型构建

文雅洁，陈 娟

（中北大学，山西 太原 030051）

0 引 言

随着互联网技术与多媒体技术的飞速发展与普及，致使以音频、图像、视频等为主要内容的多种类型作品创作、存储与传播变得极为便利。尤其是音频领域，多种编辑软件兴起与应用，数字音频已经成为现今多媒体的主要表现形式之一，受到了社会大众的广泛关注。但是，由于数字音频制作、传播过程中受多种因素的影响，使得数字音频中存在着大量的噪声信号，不但会降低音频信号的信噪比，还会影响音频信号的清晰度，为其应用与传播带来了较大的阻碍。

如何构建一个有效的数字音频降噪模型已经成为音频领域亟待解决的难题之一。就现有研究成果来看，使用较为广泛的降噪算法为一种基于小波阈值的变步长LMS 语音降噪算法[1]与启发式联合PCD 快速降噪算法[2]。前者主要应用小波软阈值分析语音信号的时频，将具有噪声特征的小波系数进行剔除，通过变步长最小均方误差算法对语音信号进行进一步的降噪处理，从而实现语音信号的降噪处理；后者将音频信号转化为信号矩阵，利用Joint-PCD 与超完备字典同时对信号矩阵进行降噪处理，获得信噪比较高的音频信号。

上述两种算法虽然能够实现音频信号的降噪处理，但是前者运行时间过长，后者降噪效果较差，无法满足数字音频领域的发展需求，故本文提出多轨道数字音频自适应变阶谱降噪模型构建。

1 数字音频自适应变阶谱降噪模型研究

1.1 预加重多轨道数字音频信号频谱估计

预加重处理后多轨道数字音频信号yi呈现非平稳特性，说明音频信号参数指标存在着一定的随机性，故采用最大熵谱估计算法估计数字音频信号频谱，为研究目标实现提供支撑。一般情况下，随机序列M阶自回归模型当前值可以用M个过去值进行估计表示[3]。依据上述理论，数字音频信号yi可以表示为：

式中：AM,m表示自回归模型系数；yi-m表示数字音频信号过去值；Ei表示白噪声估计误差[4-6]。需要注意的是，为了研究便利，将其均值设置为零。从本质角度出发可知，最大熵谱估计算法就是在特定背景下推出一系列序列[7]。因此，其等价于自回归模型，可以通过求解自回归模型的参数来估计数字音频信号频谱[8]。依据功率谱定义对式（1）进行频谱模平方运算，计算结果为：

式中：AM,m(f)表示自回归模型系数的频谱；yi(f)表示数字音频信号的频谱；Ei(f)表示白噪声的频谱。

根据公式（2）即可推导出数字音频信号频谱的表达式为：

式中Syi(f)表示数字音频信号频谱。

通过公式（3）可知，只要求解出自回归模型系数AM,m即可估计出数字音频信号频谱[9-10]。因此，此节利用最大熵估计算法对AM,m进行求解与计算。设置自相关序列为Ryy( 0 ),Ryy( 1) ,Ryy( 2 ),…,Ryy(M)，其是已知的，则自回归模型系数AM,m求解矩阵表达式为：

求解公式（4）即可获得自回归模型系数，表达式为：

式中：μM表示偏相关系数，主要以白噪声频谱PM为核心进行计算，计算公式为

将公式（5）的计算结果AM,m代入公式（3）中，即可获得数字音频信号频谱的估计结果Syi(f)，为后续降噪模型搭建提供依据。

1.2 多轨道数字音频自适应变阶谱降噪实现

以上述数字音频信号频谱估计结果Syi(f)为基础，搭建自适应变阶谱降噪模型，确定谱减阶数的自适应取值规则，将待处理的多轨道数字音频输入至训练好的降噪模型中，输出结果为降噪完成后的多轨道数字音频，为数字音频的传播与应用提供助力。自适应变阶谱降噪模型表达式为：

式中：(f) 表示降噪后音频信号频谱估计结果[11]；β表示谱减阶数；p(f)与q(f)表示谱减系数。由公式（6）可以看出，自适应变阶谱降噪模型的性能优劣由谱减系数与谱减阶数决定。其中，谱减系数最佳取值计算公式为：

式中ξ(f)表示通过直接判决法估计的先验信噪比。

在实际情况下，为了避免数字音频出现失真现象，通常会对其增益函数设定一个最低限值。若是最低限值过小，在降噪过程中极易产生失真现象，使得数字音频失效[12-13]。而谱减阶数β与增益函数之间存在着紧密的联系，当谱减阶数β较大时，增益函数数值较大，此时降噪效果较差；反之，当谱减阶数β较小时，增益函数数值较小，此时降噪效果较好。根据上述阐述内容，确定谱减阶数β的自适应取值规则，具体如下：

式中：ψ与η表示谱减阶数β自适应取值计算的辅助常数，需要根据数字音频信号实际情况进行相应的设置；γ(f)表示数字音频信号增益函数。

除此之外，为了防止谱减阶数β过小，而导致数字音频信号增益函数γ(f)过小，进而造成数字音频失真现象的发生，需要保证谱减阶数β大于最低限值0.1。将公式（7）与公式（8）计算的谱减系数与谱减阶数代入公式（6）中，即可获得降噪后的数字音频信号频谱估计结果(f)，通过逆变换将其重构为数字音频信号，表达式为：

式中：表示降噪处理后的数字音频信号表示数字音频信号逆变换函数；ρo表示逆变换因子，取值范围为[ 0,1.2 ]。

综上所述，实现了多轨道数字音频自适应变阶谱的降噪，为多轨道数字音频的应用与后续发展提供了一定的帮助。

2 实验与结果分析

2.1 实验准备阶段

构建模型在降噪多轨道数字音频信号重构过程中应用了逆变换因子ρo，其取值大小直接关系着音频信号重构质量的优劣。因此，在实验准备阶段需要对其最佳取值进行相应的确定。通过测试获得逆变换因子ρo与音频信号重构质量（采用误差来表示）之间的关系，如图1 所示。

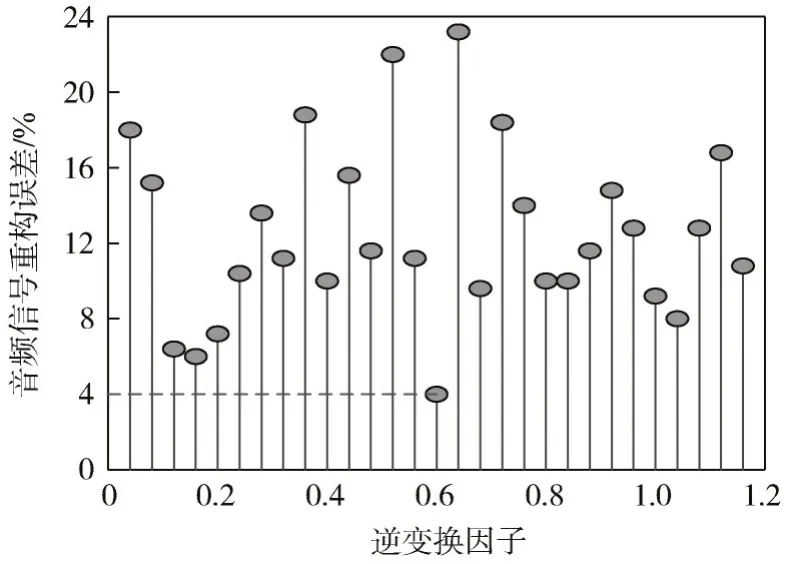
图1 逆变换因子与音频信号重构质量关系示意图

如图1 数据所示，当逆变换因子取值为0.6 时，音频信号重构误差达到最小值4%。因此，确定逆变换因子ρo最佳取值为0.6。

2.2 实验结果分析

以上述确定的逆变换因子最佳取值为基础，应用对比模型1、对比模型2 与构建模型进行多轨道数字音频降噪对比实验，获得多轨道数字音频信号降噪结果如图2 所示。

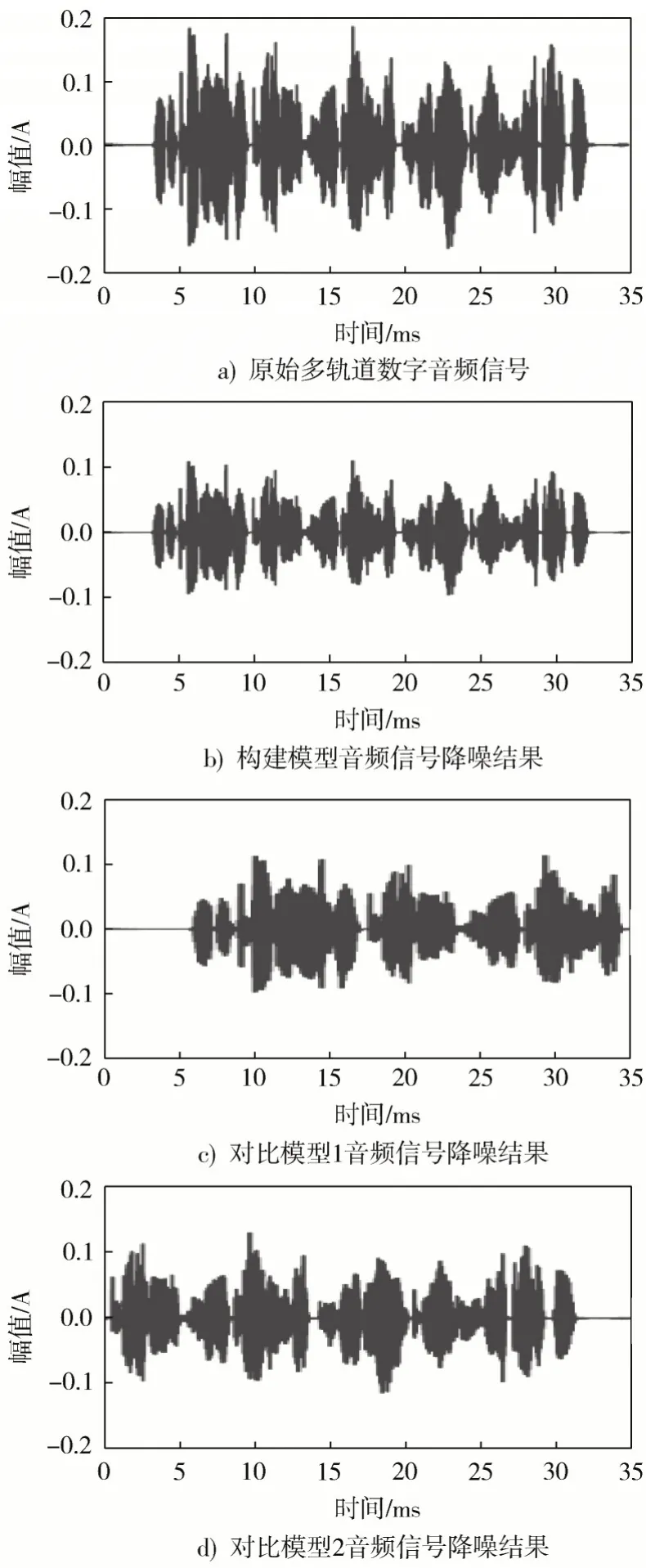
图2 多轨道数字音频信号降噪结果示意图

如图2 所示，相较于原始多轨道数字音频信号，构建模型、对比模型1 与对比模型2 应用后，均可以降低多轨道数字音频信号中的噪声信号占比，达到多轨道数字音频信号降噪的效果。但是，构建模型应用后获得的多轨道数字音频信号降噪结果是完整的，无丢失音频信号现象，而对比模型1 与对比模型2 应用后获得的多轨道数字音频信号降噪结果是缺失的，均存在部分音频信号丢失现象，破坏了音频信号的完整性，表明构建模型多轨道数字音频降噪效果更好。

3 结 语

多媒体技术的飞速发展与广泛应用，使得多轨道数字音频呈现急速增加的趋势，但是由于数字音频录制、传播设备较丰富，使得数字音频中包含着大量的噪声，影响数字音频有效信号的传播与应用，故本文提出多轨道数字音频自适应变阶谱降噪模型构建。实验数据显示，构建模型提升了多轨道数字音频降噪的性能，能为数字音频的后续应用提供更有效的方法支撑。