基于线性混合模型的腮腺炎抗体衰减模型探讨*

陈思臻 臧一腾 刘元宝 陈炳为△

【提 要】 目的 探索江苏省五市接种MMR(measles mumps rubella)疫苗儿童腮腺炎抗体衰减的情况。方法 以性别、入组年龄、接种剂次和地区作为协变量,利用线性混合效应模型探讨腮腺炎抗体与接种时长间的关系。结果 线性混合效应模型分析结果显示,性别、接种剂次与地区的差异有统计学意义,时间固定效应的参数值为-0.088,截距与时间效应的协方差为-0.094。结论 模型的ICC为0.652,个体重复测量时间内的变异较小,适合混合效应模型进行分析。腺炎抗体随时间呈现下降的趋势;基线抗体水平越高下降越快,呈现负相关关系。本次研究构建的腮腺炎抗体衰减模型对流行性腮腺炎的预防控制工作有着重要意义。

流行性腮腺炎是由腮腺炎病毒引起的急性呼吸道传染病,临床上以腮腺非化脓性炎症、腮腺区肿痛为特征,传染性强,多发于学校等儿童青少年聚集的区域[1-2]。2008年,我国将麻疹、流行性腮腺炎、风疹(简称麻风腮,measles,mumps,rubella,MMR)三联疫苗纳入国家免疫规划范畴[3]。但国内外对接种MMR疫苗后腮腺炎抗体衰减速率进行建模分析研究并不多。LeBaron等[4-6]对美国威斯康星州接种2剂次MMR疫苗的儿童进行最长达12年的随访,以探究MMR疫苗的短期及长期免疫原性;Seagle等[7]基于该队列数据使用重复测量线性混合效应模型对腮腺炎抗体浓度衰减速率进行建模。Wanlapakorn等[8]对370名泰国儿童从出生开始随访36个月,其间接种2剂次MMR疫苗,分析其腮腺炎等抗体变化趋势,但未对衰减速率进行建模。而国内相关研究更为欠缺。因此,本次研究旨在基于江苏省接种MMR疫苗儿童腮腺炎抗体的数据,构建线性混合效应模型对腮腺炎抗体变化情况进行分析。

资料和方法

1.数据来源

本次数据来源于江苏五市(常州、连云港、泰州、徐州、镇江)的一项前瞻性观察队列。队列共有3346名儿童,分为两个独立组别,一组入组时小班(3～4岁),一组入组时小学一年级(6～7岁)。两组儿童均于2015年入组,且分别于2015年、2016年和2018年进行三次采血,使用ELISA方法检测腮腺炎抗体浓度水平。两组儿童均在1.5岁前接种过1剂次MMR疫苗,部分儿童入组前接种过2剂次MMR疫苗。

2.研究方法

(1)数据处理

本次研究时间变量t定义为采血距接种1剂次MMR疫苗时间(年)。抗体浓度呈明显偏态分布,利用下式进行对数变化[9]:

yij=ln(1+xij)

其中,xij表示第i名儿童第j次测量的抗体浓度水平,单位为U/ml。使用SAS 9.4软件进行数据描述及模型构建。

(2)仅基于时间效应的抗体衰减模型

对全人群建模,自变量仅考虑时间效应,建立一般线性模型。

为探寻不同随机参数组合下模型的优劣,以儿童作为随机效应,截距项和时间效应的不同组合为随机参数,建立混合效应模型。

对于不同随机参数组合,使用赤池信息准则(AIC)、贝叶斯信息准则(BIC)及-2倍对数似然值(-2LL)判断模型拟合效果,并选取最优模型。对于最优模型,固定参数采用t检验,随机部分的方差采用WaldZ检验。

(3)纳入协变量的抗体衰减模型

为探寻不同因素对腮腺炎抗体衰减模型的影响,根据仅基于时间效应抗体衰减模型得到模型需要考虑的协变量,构建含有不同协变量组合的模型。考虑的协变量有性别、接种剂次(1剂次、2剂次)、入组年龄(小班、小学一年级)及地区。对于四个协变量,共有16种组合,使用AIC、BIC和-2LL判断模型拟合效果,并选取最优模型。

(4)混合模型的方差-协方差结构

重复测量数据的混合效应模型中,各时间点观测数值之间的相关关系可表示为等相关、自相关等不同方差-协方差结构[10]。本次研究中各时间点观测数据间关联模式不典型,且样本量较大,选择非确定相关(UN)的方差-协方差矩阵[10]。

(5)模型评价方法

本次研究使用AIC、BIC及-2LL对模型进行筛选。对于最终构建的基于时间效应的抗体衰减模型和纳入协变量的抗体衰减模型,采用混合效应模型决定系数(R2)[12]、平均绝对误差(MAE)和均方根误差(RMSE)对模型预测能力进行评价。混合效应模型决定系数R2计算公式如下:

结 果

1.人群一般信息

本次研究共收集江苏省五市共3346名接种MMR疫苗儿童的腮腺炎抗体数据,其一般人口学信息见表1,三个采血时间点体内抗体浓度对数转化后信息见表2。

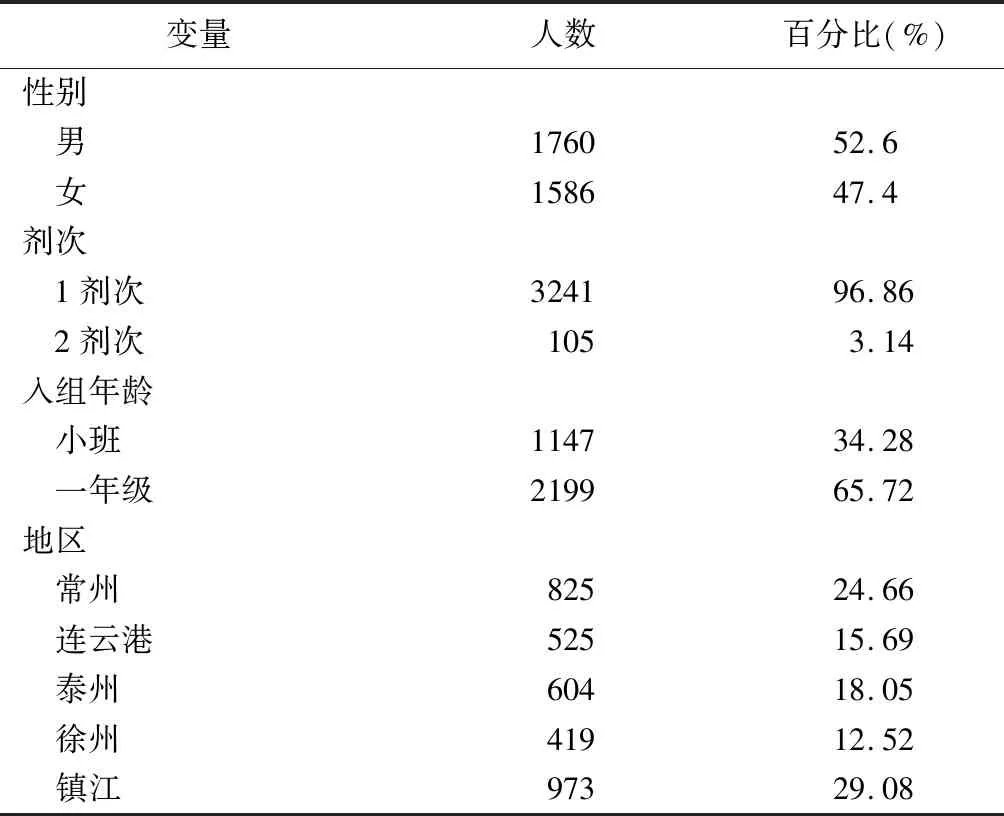
表1 一般人口学信息

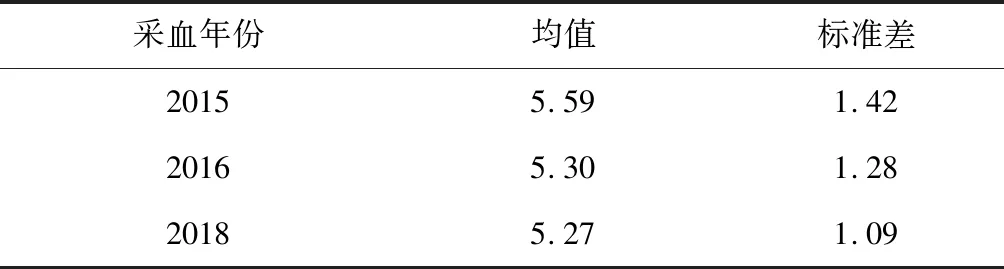
表2 各采血时间点抗体浓度对数转化值

本次前瞻性队列研究中纳入的儿童性别分布差异不大;绝大部分儿童在2015年入组前接种过1剂次MMR疫苗(96.86%);2015年入组时为小学一年级的儿童(65.72%)较小班的儿童(34.28%)多;镇江儿童最多,达29.08%,徐州儿童最少,为12.52%。

三次采血时间点抗体浓度总体呈下降趋势,且2016年与2015年间的下降幅度大于2018年与2016年间的下降幅度。

2.基于时间效应的抗体衰减模型

考虑不同参数,建立四种不同线性混合模型,其AIC、BIC及-2LL结果见表3。不设随机参数的模型1中的AIC、BIC、-2LL均高于其余模型;模型4的AIC、BIC、-2LL最低,模型最优。模型2的组内相关系数ICC为0.652,说明同一个儿童在三个时间点上的测量数据变异相对较小(个体内的数据是不独立的),而不同儿童之间的变异则相对较大,适合使用以个体因素为高水平的一般线性混合效应模型。

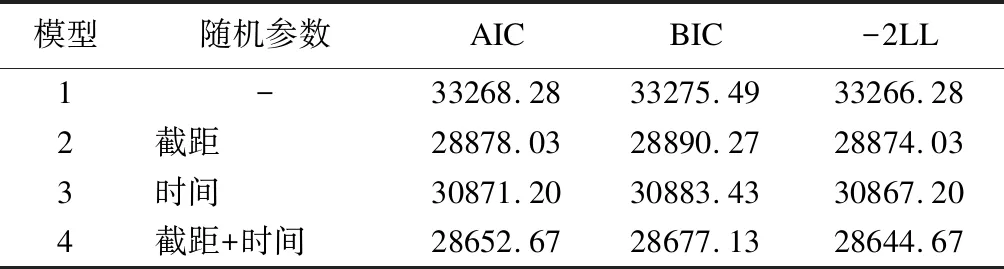
表3 基于时间效应的抗体衰减模型随机参数选择

3.考虑协变量的抗体衰减模型

表3中抗体衰减模型将截距项与时间设为随机参数时模型最优,因此在考虑协变量的抗体衰减模型中,在模型4的基础上加入不同协变量,构建一般线性混合效应模型。16种不同协变量组合的模型中,纳入性别、接种剂次和地区三个协变量的模型的AIC、BIC、-2LL最小,认为模型最优。

4.模型的评价

基于时间效应的抗体衰减模型与纳入协变量的抗体衰减模型结果如表4。模型抗体衰减固定效应轨迹图见图1。

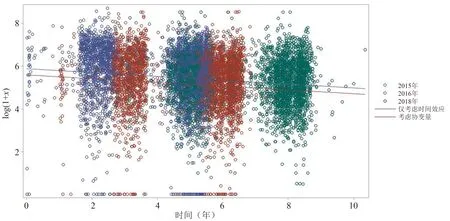
图1 模型抗体衰减固定效应轨迹图

表4 各模型固定参数、随机参数和拟合统计量

仅考虑时间效应的模型中,所有固定参数均有统计学意义;在随机效应中,模型总方差、初始状态方差、初始状态与时间变化斜率的协方差均有统计学意义。协变量模型的固定参数仅连云港地区无统计学意义;随机效应中,所有随机项方差或协方差均有统计学意义;仅考虑时间效应的模型R2和MAE略优于纳入协变量的模型,RMSE略差于纳入协变量的模型。图1可见,不论是否考虑协变量,腮腺炎抗体随时间下降速率差别不大;但经协变量校正后,认为基线抗体水平降低。腮腺炎抗体随时间呈现下降的趋势(其系数为-0.088),截距与时间变化呈现下降趋势,抗体水平越高下降越快,呈现负相关关系(-0.094)。

讨 论

本次研究基于时间效应构建线性混合效应模型,发现不设随机参数的模型表现最差,说明线性混合效应模型在重复测量的纵向数据资料中的表现优于一般线性模型。

将协变量纳入模型后,时间效应的固定参数变化不大,模型拟合效果提升,但预测能力差异不大,可能与协变量和时间效应之间的相关性有关。本次研究与Seagle等[7]研究结果相比,所得抗体浓度随时间下降速率较慢;相比于男性儿童,女性儿童抗体浓度平均水平较高;相比于入组时接种1剂次MMR疫苗的儿童,接种2剂次MMR疫苗的儿童抗体浓度平均水平较高;泰州为所有研究地区中抗体浓度平均水平最低的,其次为连云港,两者间无统计学差异。

本次研究使用混合效应模型对江苏省五市儿童腮腺炎抗体衰减进行描述预测,考虑了不同个体间的差异,将个体设为高水平变量,提高了模型预测能力,对流行性腮腺炎的预防控制具有重要意义。本次研究中混合效应模型考虑腮腺炎抗体衰减与具体时间的变化关系,但每个个体的重测时间点偏少(仅三次测量),可能会影响模型的准确性,需后续研究采用更多数据进行验证。