设计实践与地域性维度的教学方法评测

傅游磊 梁桂嘉

摘要：科学的创意思维法有助于创新力和设计教育的发展。然而尚未有通用的适合设计教学使用的思维法，因此，本研究依据大学设计教育的办学思路以及学生特点将创意思维法转变成设计教学方法，从“设计教学实践”与“地域性主题”两个维度进行适用性评测。提出德尔菲法与二元模糊语意模型结合的评测模式，使用三角模糊数、欧式距离法、OWA等算法对15位专家的评估值进行统计分析。筛选出11类创意思维法最适用于设计教学，表明大学设计类教师对于方法应用的基本观点。所评估筛选的创意思维方法对于大学的设计类课程的教学具有一定的参考价值，并首次提出将二元模糊德尔菲法结合到该领域。

关键词：创意思维 地域性 设计教学 二元语意变量 模糊德尔菲法

中图分类号：G644.4 文献标识码：A

文章编号：1003-0069（2023）21-0082-05

Abstract：The scientific method of creative thinking contributes to the development of innovation and design education. However，there is no universal thinking method suitable for design teaching，so this study transforms the creative thinking method into a design teaching method based on the thinking of university design education and students characteristics，and evaluates its applicability from two dimensions：“Design Practice” and “Locality”. The applicability of the method is evaluated in two dimensions："design teaching practice" and "regional themes". A Delphi method combined with a binary fuzzy semantic model was proposed，and the evaluation values of 15 experts were statistically analyzed using the triangular fuzzy number，Euclidean distance method，and OWA algorithms. Eleven categories of creative thinking methods were selected as most applicable to design teaching，indicating the basic views of university design faculty on the application of the methods. The evaluated and screened creative thinking methods have a certain reference value for teaching design courses in universities，and for the first time，the binary fuzzy Delphi method is proposed to be combined into the field.

Keywords：Creative thinking Locality Design teaching 2-Tuple linguistic Fuzzy Delphi method

引言

創意思维法的学习主要培养设计思维能力，使其具备创意自信，能自我创新的人才[1]。并非所有的创意思维方法都适合于设计教学实践课程特征，需要分析创意思维方法与教学结合的适用性，依据办学思路以及学生特点，将相似的方法整并或者移除不适用的方法。然而，西方倡导的全球化的弊端让“地域性”设计课题受到广泛的关注和重视，因此，本研究为解决地域性设计教学中的创意思维法的评估和选择问题，提出了一种基于群体决策的二元模糊语意表示模型的运算与迭代方法，通过设计类教师的教学经验评估方法的适用效果。

一、研究介绍

（一）创意思维与设计实践

创意思维的程序基本上可以总结为非线性发展的5个阶段，可以因实际面对的问题进行扩展或缩短，更可以循环与重复。IDEO将其定义为：发现、解读、构思、实验、发展5个部分阶段；而d.school则定义为：移情、界定、构思、原型、测试五大行动模式；Scheer等人定义了6个阶段的思维过程[2]。创意思维是设计和创新中最相关的领域之一。通过研究Rauth等人发现通过创意思维应用可以实现不同水平的创造性知识、技能和思维模式，最终形成一种被称为“创造性信心”的能力。创意思维展现了如何有助于设计创造力的发展和理解[3]。

（二）地域性与设计教学

地域性设计强调“地域性”，是在不断的现代化、都市化、全球化、符号消费化等变迁冲击下所产生的一种重整反应，重整因强势西方现代化所忽视的在地特质，如：气候、材料、文化特性、社群特征（也就是地理、人口、社会发展等）等[4]。地域性的尺度概念是一种具有相对性的边界范围，从文化区域、民族和国家，到特定的行政地理范围，以及村落、社区或街道等[5][6]。将“地域性”作为一种设计概念的教学实践，以适应时代发展的特点以及地域自然条件和人文条件特点为根本，提倡设计与地域相结合，其中包括设计与文脉、设计与环境、设计与行为、设计与材料、设计与产业等。地域性设计教学要求在课程中进行理论讲解、调研观察、问题分析、概念讨论、方案设计和设计评估等流程。

二、研究流程与方法

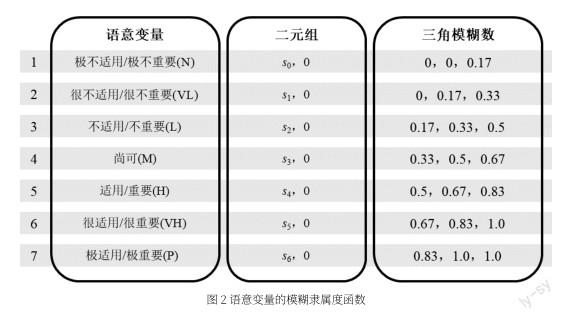
本研究所提出的设计教学方法适用性评测方法是基于二元模糊德尔菲法，具体流程如图1所示。第一步需要定义设计教学方法的类别，通过建构设计教学方法的选择问卷，然后使用德尔菲法进行专家评估来实现；第二步为明确评测的工具而定义三角模糊函数与语言变量，确定使用的二元模糊语义模型与有序集；第三步为设定“地域性主题”与“设计教学实践”两个维度在设计教学中的权重值，通过建构问卷获取专家的权重评估值；第四步为教学方法的适应性评测，首先定义评估模型Dapp，再建构问卷来获取专家的适用性评估值，然后将评估值转化为三角模糊数进行整合，并获得解三角模糊数，最后用OWA算法将“地域性主题”与“设计教学实践”二维度进行聚合运算，得到适用性评估值；第五步为评估值的二元模糊语意转化，用以确定适用性最大化的设计教学方法；最后进行最优的设计教学方法确定，如果未获得合适的方法，可再回到第一步修正所定义的教学方法类别。

（一）模糊集与德尔菲法理论

1.模糊德尔菲法的专家评估

德尔菲法是以科学性的方法，汇整专家学者对特定主题或事件一致性意见的研究方法[7]。为弥补传统德尔菲的专家意见分歧和理解不清楚等缺点，模糊理论与德尔菲结合（Fuzz Delphi Method，FDM）的方法被提出[8][9]。通常模糊德菲法邀请的专家人数约在10～15人之间[10]。专家的遴选应考量其具有一定代表性的专业背景，同时对于意见咨询的主题具有高度的专业知识，本研究从福建省的6所本科高校中选择环境设计、产品设计、视觉传达设计专业的教师为专家团体，共20名成员，其中第一轮与第二轮参与调查的专家数量为5人，第三轮的数量为15人，以此再分析与验证所筛选方法在“设计教学实践”与“地域性主题”属性的适用性。

2.定义模糊语意变量

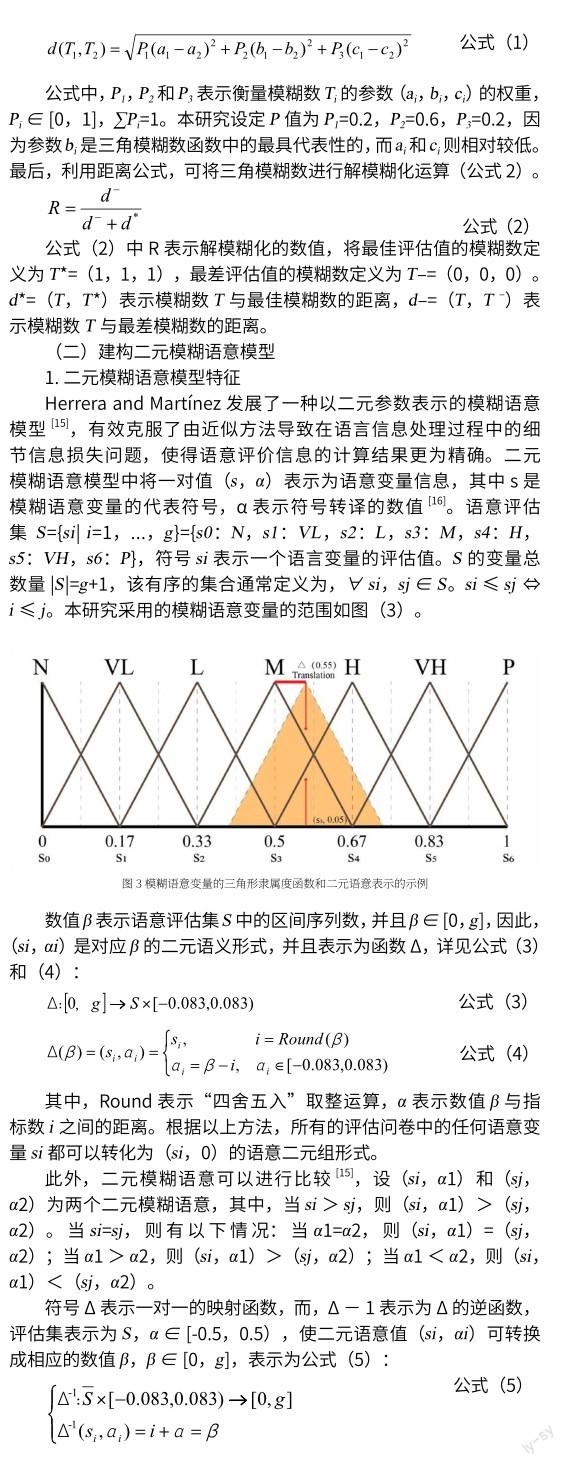
对模糊或难以定义事物，传统量化表示方式很难合理的描述与衡量，故适合以语意变量的概念来处理[11]。Klir和Folger以语意变量与三角模糊数结合建立专家问卷之评估值[12]，并应用在德尔菲法的中，其三角模糊隶属度函数表示以及数学运算根据Kahraman等人的研究文献[13]。

本研究的“适用程度”和“重要性”评估系采用7等级量表，如图（2）：

三、研究评估结果

（一）德尔菲法

1.教学方法选择

将创意思维法与大学的设计教育过程结合，并建构成教学方法应用在地域性主题课程中，这是本研究的基本目标。研究实验的第一阶段需要先从100多种的方法中初步选择出与地域性设计教学课程相适配的方法。5位教师组成专家小组初步归纳整理资料，并重点分析了方法在使用过程的优点与缺点，结合专家成员的探讨进行深入的分析与思考。此外，基于小组的讨论与分析，并归纳选择出71个。但由于筛选出的方法中存在类型相似、目的和操作过程类似的情况，只有针对的对象以及发展的方向有区别，比如参与式观察法更强调研究者的参与，隐蔽观察与之相反，突出研究者的不干预，因此可以将它们归属于观察法的类型。专家小组将71个方法按照特征分类为22类，并一致地认为这些类别方法在地域性设计教学中具有实用性，虽然其中的一些方法很少在过去的教学中被使用，但其理念的先进性与可用性被认为具有潜在的适用性优势。

2.教學方法的原始评估值

研究实验的第二阶段则是专家小组成员（n=15）将22类方法进行设计教学的适用性评估，并以德尔菲法的流程进行实验。评估内容包括“设计教学实践”与“地域性主题”的属性比重与教学适用性评估两方面。由专家组成员发挥各自专业经验，独立地表达判断的意见。该步骤进行二轮的问卷评估，第一轮的评估中有些教师对于部分方法的内容与应用方式不熟悉，如互联网调研、原型探讨和参与性研究等，因此需要进行第二轮评估通过加强对方法的解读，以消除困惑与歧义，其中评估二属性比重问卷采用100分值的尺度。数据结果所示，将15位教师的评估数据整合，设计教学实践属性的平均比重WE=48.4，地域性主题属性的平均比重WY=51.6。

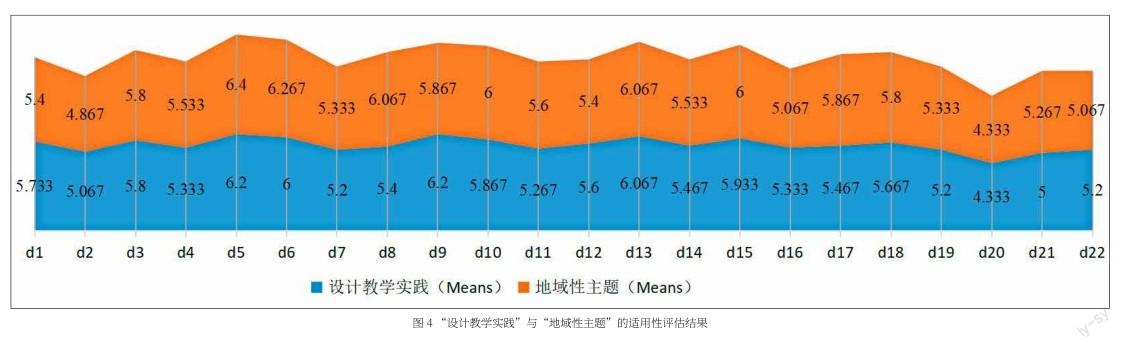
教学方法的适用性评估问卷采用7级语意量表（图2），用数值表示适用性程度。图（4）中表示了基于设计教学实践的教学方法适应性评估数据结果，将15位教师的原始评估值进行整合，其平均数范围4.333-6.2，最高值的方法为d5（思维发散）和d9（用户体验），其次为d13（观察调研法）。

图（4）表示了基于地域性主题的教学方法适用性评估数据结果，将15位教师的原始评估值进行整合，其平均数范围4.333-6.4，最高值的方法为d5（思维发散），其次为d6（资料分析）。从数据的结果中，所有的方法在设计教学实践与地域性主题的两个角度中的适用性均达到4分值（尚可）以上，说明所归纳的22类方法符合地域性设计教学的基本要求。

3.二元模糊语意变量的评估值

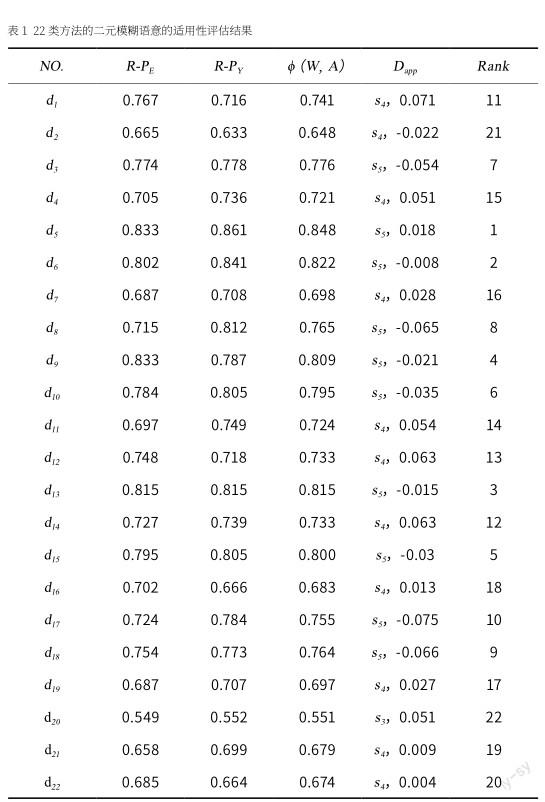
将教学方法适用性评估原始评估值转换为三角模糊数后，将15位教师的模糊评估值进行整合，再用欧式距离法（Euclidean distance）将模糊数近似化（公式1），最后采用公式（2）可将三角模糊数进行解模糊化运算。如表1所示，R-PE表示方法从设计教学实践属性的角度考虑，其适用性评估值的解模糊数，数值范围为0.549-0.833。R-PY表示方法从地域性主题属性的角度考虑，其适用性评估值的解模糊数，数值范围为0.552-0.861。

4.教学方法的适用性选择结果

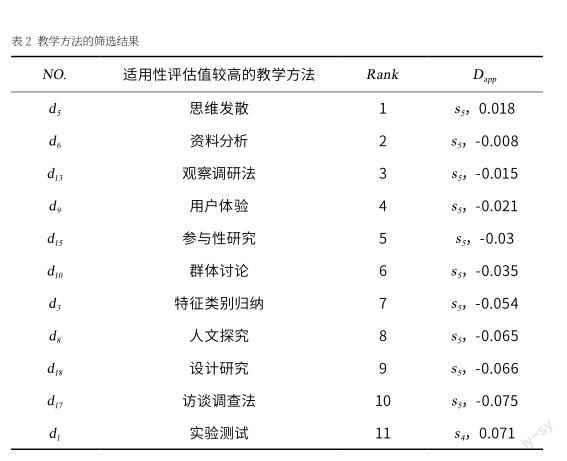
本研究根据公式（8）定义的适用性最大化函数MAX50%Dapp与方法，对于22类教学方法进行筛选，根据二元模糊语意评估值由大至小排列，并以总数的前50%为选择标准。如表2所示，选择出适用性评估值较高的11个教学方法，选择的结果代表了专家组每位教师对每个教学方法的适用性的专业判断，并做出客观合理的群体决策。

四、研究结果讨论

本研究提出将二元模糊德尔菲的适用性评测法应用在地域性设计教学方法的筛选应用中，借由具有丰富设计教学经验的大学教师的专业判断力，通过群体决策的方式获取评估值，并筛选适合设计教学使用的创意思维方法。相比过去的研究，本研究所提出的适用性评测方法具有3个主要的创新之处，具体如下：

（一）二维度的评测模型

提出了一种二维度（“设计教学实践”和“地域性主题”）的评测模型，通过OWA算法整合专家对于两种维度的看法，从而使适用性的评测由一维升级为二维。在设计教学中对于方法的适用性评测是难以量化的问题，使用二元语意变量来处理有很大的助益，也较符合评估者的判断和表达方式，同时还增加了决策结果的精度。此外，该模型的应用不仅限于此，还可以依据研究的内容定义评估属性集合P={PE，PY}。

（二）二元组语意变量表示专家决策

使用德尔菲法获取多位专家的意见，并用三角模糊数与欧式距离法进行整合，可以避免专家之间出现较大的分歧，有利于将评估值整合为更客观态度。每个教学方法的适用性评估值都由一个二元组表示，因此，使用二元组的最大化函数可以很容易地比较两个评估。这个函数截集的设定是依据本研究的需求而设定，将有助于展示和理解所提出的具有二元模糊语意变量的教学方法的适用性选择。

（三）教学方法的应用

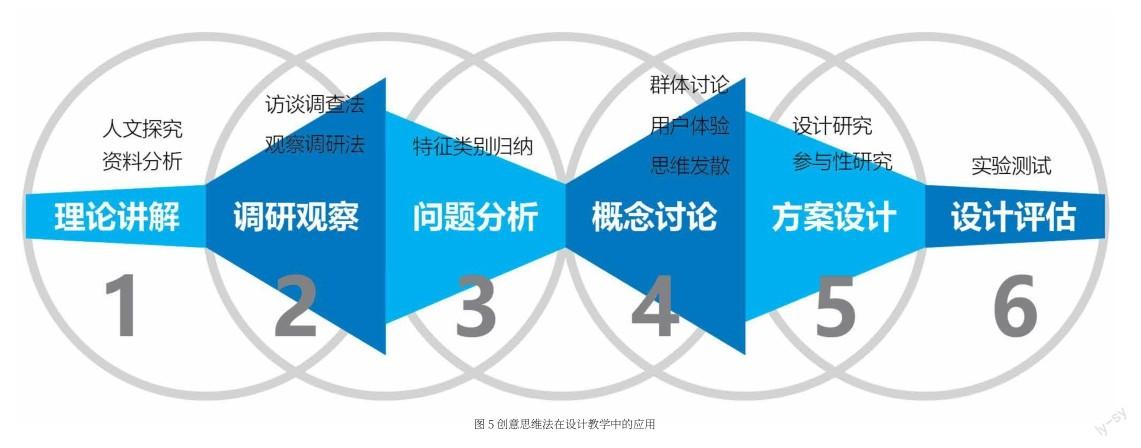
圖5所示，本研究所筛选的11类创意思维方法适合被对应使用在6个阶段的设计教学中，使学生在设计专业学习与实践的过程中，在科学的方法和清晰的逻辑辅助下发挥最大的创造力。具体分析如下：

1.第一阶段为“理论讲解”，可以选用人文探究或资料分析对课程的主要设计目的和内容进行定义与讲解，其中人文探究是一种探索性调研方法，深入体验了解用户世界并获得用户亲身经历的想法和见解，更好地表达了对生活、环境、理念和互动行为理解的启发性工具；资料分析是运用多种来源的研究证据，分析已经完成和未完成的案例，收集对比数据，深入真实情景中单一事件或情况的研究策略，提出建议并帮助设计者在目前的研究中确定研究方向和方法。

2.第二阶段为“调研观察”，建议使用访谈调查法或观察调研法进行用户、情境与场所等探索对设计问题点进行定义，其中访谈调查法是以书面形式的收集描述信息资料的工具，可以了解受访者对于某一事物的特点、思想、行为、观念、看法或态度；观察调研法是细心观察各种现象并做出系统性的记录（图文和音频），包括观察人物、组件、环境、事件、行为和互动过程，也可以通过参与活动、情境、文化和次文化来了解各种情况和人们的行为。

3.第三阶段为“问题分析”，使用特征类别归纳方法对设计问题点进行具体分析，此类方法属于归纳性行为，可以帮助理清思路建立共识，是一种从下往上的归纳性方法，可以有效收集观察结果和观点，并形象地将其分类出普遍的、重要的主题。

4.第四阶段为“概念讨论”，适合选用群体讨论、用户体验和思维发散等方法解决设计问题点与概念构思，其中群体讨论类似于小型研讨会，提供了一个可以自由探讨和分享理念的合作的空间，通过群体所创造出的活力，不断激发无数创意和解决方案，为项目任务探索设计理念；用户体验是以同理心的途径捕捉用户完成某个任务或实现某一目标时的所做、所想和所用，以用户为中心进行思考；思维发散是通过感性或理性的思维，集思广益形成一个特定的主题，开发核心概念或寻找核心问题，找出特点、论据以及相关想法，敢于打破并挑战惯性思维模式。

5.第五阶段为“方案设计”，可以选用设计研究或参与性研究辅助概念方案的创作，其中设计研究是在设计过程中把模型和理论与技术结合到一起，优化设计实践；参与性研究是使设计参与者发挥创造性的洞察力，表达自己的情感、梦想、需求和愿望，从而为概念设计提供了丰富信息。

6.第六階段为“设计评估”，可以尝试采用实验测试对设计方案的进行成效评估，该方法不是依靠直觉和传闻，紧密联系测试证据和实际应用，通过实验评估工具、设备、装置、场所或环境，测量事物之间的联系与设计效果。

结论

本研究提出使用一种基于群体决策的二元模糊德尔菲法，并以思维方法在设计教学中的适用性评估研究为案例进行验证，可以通过5个步骤执行，具有较强的可操作性，并且运行成本较低，所发展出的问卷较符合填答者的习惯。结果表明其具有运算简便、语义明确、提高评估决策的精度，使模型具有优良的操作性，适应范围广泛。感知的现实表现是定性的方面，这需要语言变量。我们使用二元模糊语言表示，以避免一些模糊语言方法在聚合语言变量时遭受的信息丢失问题。对每个教学方法的评估都是基于这些感知的聚合来进行的，而这些评估促进了决策过程。目前为止，首次将二元模糊语言模型结合到地域性设计教育应用领域，并用于筛选恰当的教学方法。

对于后续的研究，我们计划将基于二元模糊语义分析教学方法的适用性扩展到两个方向。一方面，计划在研究的系统中纳入其他的决策启发式方法，使它们能够处理模糊的语言信息。教学方法和流程在实际的设计课程教学中几乎是动态的。例如，如果学生在某阶段的学习效果不佳时，则需要返回到上一步的教学内容，或者需要改变一些方法以适应学生对知识的掌握能力。此外，为了适应线上与线下结合的教学模式，需要不断增加或调整教学方法，因此，相对较高的动态性可能会更实际地模拟专家的决策策略。另一方面，我们计划通过现实性的教学实践来验证和扩展我们所筛选的教学方法，以构建适应地域性设计教学，并具备较高创新性与实用性方法。

基金项目：福建省教育科学“十四五”规划2021年度课题，“创新思考法与地域性设计教学融合实证研究”（项目编号：FJJKBK21-025）

参考文献

[1]Bella M，Hanington B. Universal methods of design[M]. Beverly，MA：Rockport Publishers，2012.

[2]Scheer A，Noweski C，Meinel C. Transforming constructivist learning into action：Design thinking in education[J]. Design and Technology Education：An International Journal，2012，17（3）：8-19.

[3]Rauth I，K？ppen E，Jobst B，Meinel C. Design thinking：An educational model towards creative confidence[C]. In DS 66-2：Proceedings of the 1st international conference on design creativity（ICDC2010），2010：1-8.

[4]吴桂阳，高小倩，邓慰先. “地域性”建筑文化与住居环境设计——以苗栗“好客屋”设计操作课题为例[J]. 建筑学报，2007，（60）：227-246.

[5]Geertz C. “Local Knowledge” and Its Limits：Some “Obiter Dicta”[J]. The Yale Journal of Criticism，1992，5（2）：129.

[6]Nordhoff M，August T，Oliveira N A，Reinecke K. A case for design localization：Diversity of website aesthetics in 44 countries[C]. In Proceedings of the 2018 CHI Conference on Human Factors in Computing Systems，2018：1-12.

[7]Noorderhaven N. Strategic decision making[M]. UK：Addsion-Wesley，1995.

[8]Yaakub M Y，Hamzah M I M，Nor M Y M. Pengesahan instrumen soal selidik kepimpinan distributif menggunakan kaedah fuzzy delphi[J]. Jurnal Kepimpinan Pendidikan，2020，7（2）：58-70.

[9]Yasin A A，Masri R，Adnan M. Application Of Fuzzy Delphi Method In Designing A Basic Teaching Model Based On Moral Values In Stem Mathematical[J]. Journal of Positive School Psychology，2022，6（3）：4898–4920.

[10]Zahedi J，Salehi M，Moradi M. Identifying and classifying the financial resilience measurement indices using intuitive fuzzy DEMATEL[J]. Benchmarking：An International Journal，2022（ahead-of-print）.

[11]Zadeh L A. The concept of a linguistic variable and its application to approximate reasoning[J].Information Science，1975，8：199-249.

[12]Klir G J，Folger T A. Fuzzy sets，uncertainty，and information[M]. USA：Prentice Hall，1988.

[13]Mendel J M. Uncertain rule-based fuzzy logic systems：Introduction and new directions[M]. N. J.：Prentice Hall PTR，2001.

[14]Chen C T. Extensions of the TOPSIS for group decision-making under fuzzy environment[J]. Fuzzy sets and systems，2000，114（1）：1-9.

[15]Herrera F，Martínez L. A 2-tuple fuzzy linguistic representation model for computing with words[J].IEEE Transactions on fuzzy systems，2000，8（6）：746-752.

[16]Dong Y，Zhang G，Hong W C，Yu S. Linguistic computational model based on 2-tuples and intervals[J]. IEEE Transactions on fuzzy systems，2013，21（6）：1006-1018.

[17]Giráldez-cru J，Chica M，Cordón O，HerrerA F. Modeling agent‐based consumers decision‐making with 2‐tuple fuzzy linguistic perceptions[J]. International Journal of Intelligent Systems，2020，35（2）：283-299.

[18]王开莹.融入創意思维训练课程的高等职业教育展示设计教学实验构想探究[J].设计，2023，36（11）：111-113.