基于单挡板的MDM波导侧向耦合谐振腔的Fano共振及传感特性

刘加堂，李石磊，齐雅楠，陈帅

（山东理工大学 物理与光电工程学院，淄博 255049）

0 引言

当入射光子照射到金属与介质的交界面时，在交界面处入射光子会和金属表面的自由电子发生相互作用，从而形成表面等离激元［1］（Surface Plasmon Polaritons，SPPs），表面等离激元具有克服衍射极限的能力，对电磁场能量具有局域增强效应，由此可以在亚波长尺度下实现对光的操作，使器件的小型化和集成化成为现实［2-4］。

近年来，研究人员提出了各种各样的波导器件，其中金属—介质—金属（Metal-Dielectric-Metal，MDM）波导［5-6］器件是应用最为广泛的一种，研究人员基于SPPs 设计出了多种MDM 的波导器件，如传感器［7-8］、全光开关［9］、滤波器［10-11］、慢光设备［12-16］。

由较窄的离散态与较宽的连续态相互耦合形成的Fano 共振［17］越来越受到人们的关注。CAO Tun 等利用相变超材料在低功率下实现快速调谐双Fano 共振［18］，提出了不对称等离子体纳米结构中的Fano 共振——亚10 nm 对映体的分离［19］，并且利用Fano 增强的可见光区手性力对手性纳米颗粒进行横向分选［20］。CHEN Jianfeng 等提出了基于分环腔耦合MIM 波导中多Fano 共振的折射率传感［21］。Fano 共振谱是尖锐且不对称的共振谱线，对结构几何参数和介质折射率非常敏感［22］。因此，研究人员将表面等离激元与Fano 共振相结合，设计出了许多高灵敏度的折射率传感器，例如2018年塞尔维亚Novi Sad 大学的研究人员JANKOVIC N 等基于等腰三角形谐振腔提出了创新设计，使系统产生四重Fano 共振效应［23］，最终得到该结构的最大品质因数（Figure of Merit，FOM）值达到3.2×105。张燕君等提出了含金属单挡板的直波导耦合类云朵腔的结构［24］，得到该结构在第一种模式下的FOM 值为5.08×104，第二种模式下的FOM 值为3.56×105，第三种模式下的FOM 值为1.17×103，其对应的灵敏度分别为600 nm/RIU，800 nm/RIU，1 083 nm/RIU。赵亚萍等设计了含金属挡板的直波导耦合半圆环谐振空腔结构［25］，得到该结构在第一种模式下的FOM 值为3.05×105，灵敏度为800 nm/RIU，在第二种模式下的FOM 值为4.59×105，灵敏度为1 160 nm/RIU。张颖秋等设计了含双挡板直波导耦合一个侧边谐振腔的结构［26］，得到该结构的FOM 值为1.29×104，最大灵敏度为1 333.5 nm/RIU。尤鑫晨等设计了含金属挡板的直波导耦合H 型谐振腔的结构［27］，最终得到该结构第一个Fano 共振峰对应的灵敏度为750 nm/RIU，第二个Fano 共振峰对应的灵敏度为1 360 nm/RIU。陈颖等提出了亚波长介质光栅/MDM 波导/周期性光子晶体中双重Fano 共振的形成及演变规律分析［28］，在最优条件下，共振A 区（Fano Resonance a，FRa）和共振B 区（Fano Resonance b，FRb）的FOM 值可达460.0 和4.00×104，共振B 区FRa 和FRb 的FOM 值可达到269.2 和2.22×104。LIU Feng 等设计了一种基于内置椭圆环形腔的温度纳米传感器［29］，其FOM 值最大为58.7，灵敏度最高为2 220 nm/RIU。祁云平等设计了基于Fano 共振的金属—绝缘体—金属—石墨烯纳米管混合结构动态可调折射率传感器［30］，在最佳结构参数下，该系统的灵敏度可达1 250 nm/RIU，品质因数为42.4。

本文提出了基于单挡板的MDM波导侧向耦合谐振腔结构，通过时域有限差分法（Finite Difference Time-domain，FDTD）对该结构进行了数据仿真，具体研究了结构几何参数与介质折射率对结构的灵敏度和品质因数的影响。

1 模型构造与理论分析

1.1 模型构造

图1所示为本文提出的结构模型，含金属单挡板的MDM 直波导侧向耦合谐振腔结构。其中金属挡板厚度设为t=25 nm，为了确保只有横磁（TM）模在波导中传播，把波导宽度设为w=50 nm，g为谐振腔与直波导的耦合距离，R为谐振腔圆的半径，a为谐振腔内银（Ag）正方形的边长，k为Ag 正方形的拆分距离，整个结构对金属挡板的中线呈对称结构，R、a、k、g的初始值分别设为R=300 nm、a=190 nm、k=10 nm、g=15 nm。图1 中的灰色区域为Ag 金属，其介电常数由JOHNSON P B 的实验数据提供［31］，白色区域填充空气介质，其中空气介质的相对介电常数εd=1。

图1 本文提出的结构模型Fig.1 The proposed structural model

1.2 理论分析

通过解二维圆形腔中的亥姆霍兹（Helmhotz）方程，可以得到圆形腔的共振条件关系式为［32-33］

利用多模干涉耦合模理论（Multimode Interference Coupled Mode Theory，MICMT）可以解释该耦合系统所形成的Fano 共振［34］。MICMT 方程为

式中，an和ωn分别为第n个模式的场振幅和共振频率；τn0为谐振腔中第n个共振模式的内损耗衰减时间；τn1和τn2分别表示波导与谐振腔中第n个共振模式之间的耦合衰减时间；κn1和κn2分别表示波导与谐振腔中第n个共振模式的耦合系数；θn1和θn2分别为谐振腔中第n个共振模式与波导S1和S2相耦合时的耦合相位；ϕn为谐振腔中第n个共振模式在输出端的相位与输入端的相位之间的差值；si±为每个波导中的场振幅（i=1，2，从谐振腔中输出为（-）或输入为（+））；sn，1+和sn，2+为每个波导中第n个模式的场振幅（i=1，2，从谐振腔中输出为（-）或输入为（+））。对于对称系统来说，τn1=τn2=τn。根据MICMT 方程，当s2+=0 时，从波导S1传输到波导S2的复振幅透射系数可以表示为

则等离子体系统的相应的透射率为T=|t|2。

对图1所示结构通过FDTD 软件数据仿真作出的透射谱线如图2所示，其图2（a）中蓝色虚线为只有金属挡板、无侧向耦合谐振腔时所形成的透射率谱线，此时谱线呈现较低的透射率，这是由于引入金属挡板后大部分SPPs 波被反射回来，从而导致透射率较低，此时形成的谱线是一个较宽的连续态谱线。红色实线为只有侧向耦合谐振腔、无金属挡板时所形成的透射率谱线，此时会在λ=741 nm、λ=782 nm 和λ=1 416 nm处形成三个共振波谷，但在λ=741 nm 处共振波谷的透射率仍然较大，所以与连续态相互干涉时此波长处并未形成Fano 共振，因此，本文所指的Fano 共振仅是指λ=782 nm 和λ=1 416 nm 处的共振波谷参与干涉形成的Fano 共振，这时形成的谱线可以看作是在λ=782 nm 与λ=1 416 nm 处形成两个较窄的离散态谱线。对于既含有金属挡板又含侧向耦合谐振腔所形成的透射率谱线如图2（b）所示，此时谱线为金属挡板所产生的较宽连续态与谐振腔所产生的两个较窄离散态相互干涉产生的两个尖锐非对称的Fano 共振峰，其Fano共振峰对应的波长分别为λ=781 nm 和λ=1 414 nm，两个共振峰分别记为FR1 和FR2。

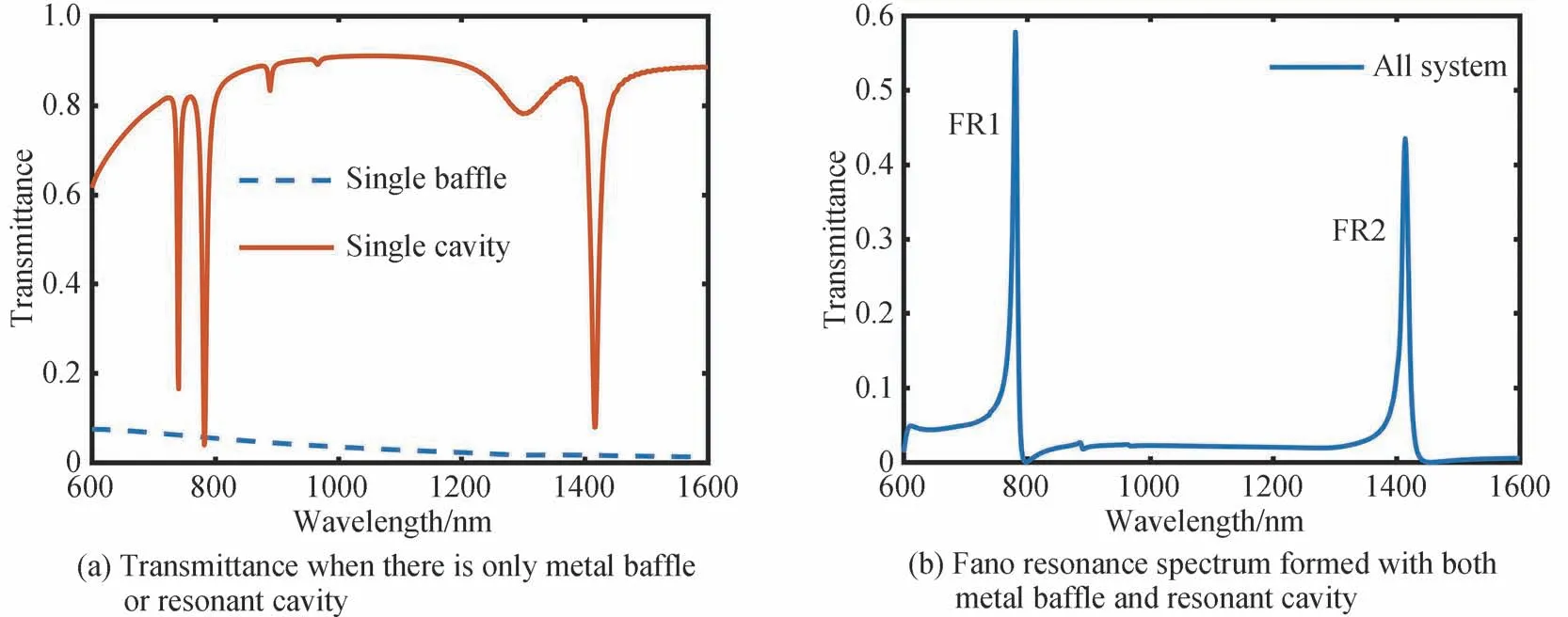
图2 Fano 共振的形成过程Fig.2 Fano resonance formation process

为了更好地解释Fano 共振的形成机理，图3 作出了共振峰及共振谷的磁场分布，图3（a）、（c）表示λ=781 nm 和λ=1 414 nm 时Fano 共振峰的磁场分布，这时的波长符合式（1）所表达的共振波长条件，大部分SPPs 波会从入射波导耦合进谐振腔中，并在谐振腔内发生共振，因此大部分能量会聚集在谐振腔内，谐振腔中的能量得到显著提高。极少部分SPPs 波会穿过金属挡板进入出射波导。当谐振腔内的共振能量再通过近场耦合到出射波导中时，会和穿过金属挡板的SPPs 波因相位相同而发生干涉相长，因此会在波导出射端口测得较高的透射率，从而形成Fano 共振峰。图3（b）、（d）表示λ=798 nm 和λ=1 456 nm 时Fano 共振谷的磁场分布，这时SPPs 波的波长并不满足式（1）的共振波长条件，所以SPPs 波在入射波导中传至金属挡板左侧时，被金属挡板反射回入射端，从而使SPPs 波不能传到出射端口，大部分能量只会聚集在入射波导中，因此在出射端测得了极低的透射率。

图3 两个Fano 共振在波峰和波谷处的磁场分布Fig.3 The magnetic field distribution of the two Fano resonances at the peak and valley

如图4所示，这两个Fano 共振的电场能量主要分布在中心正方形的拆分间距内及正方形周围，这与图3所示的磁场能量聚集区域有所不同，磁场能量主要集中在圆形腔的边缘附近。但从图4 中可发现电场的透射情况与图3所示的磁场透射情况一致。

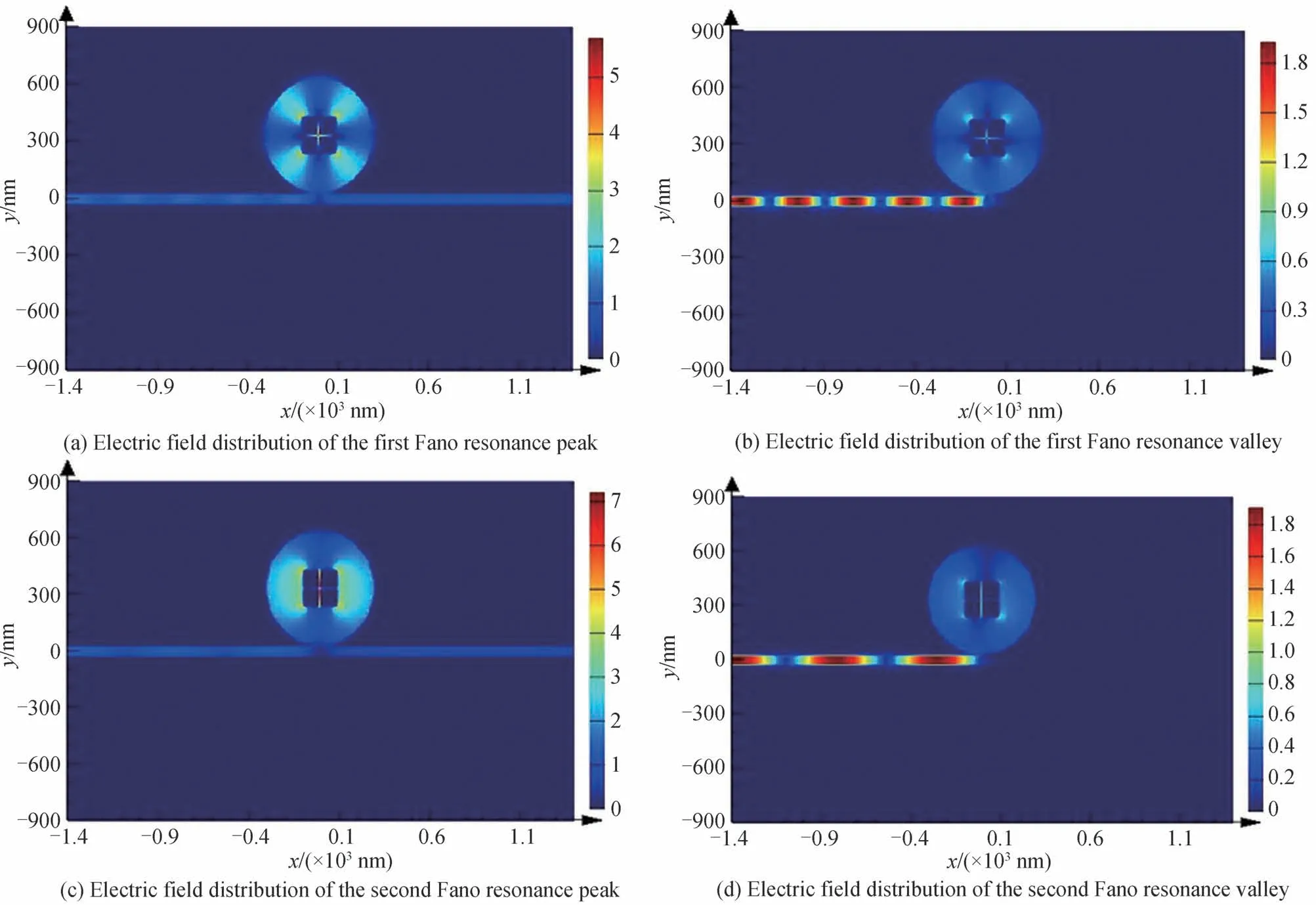
图4 两个Fano 共振在波峰和波谷处的电场分布Fig.4 The electric field distribution of the two Fano resonances at the peak and valley

2 结构几何参数对传感性能的影响

一般使用灵敏度S与FOM 值来衡量折射率传感器的性能。S［35］和FOM［36］的公式分别为

式中，灵敏度S的单位为nm/RIU，Δλ表示介质折射率变化前后共振峰波长的变化量，Δn表示介质折射率的变化量，ΔT表示介质折射率变化前后系统的透射率变化量，T表示介质折射率变化前的系统透射率，FOM是一个无量纲参数。

2.1 圆半径对系统传感性能的影响

当谐振腔中心Ag 正方形的边长a=190 nm，拆分距离k=10 nm，耦合距离g=15 nm 时，对谐振腔的圆半径R从270 nm 至330 nm 进行参数化扫描，得到圆半径R=270，280，290，300，310，320，330 nm 时Fano 共振峰透射率曲线如图5（a）所示。可以看到，随着R的增大，FR1 和FR2 的透射率均有增有减，但总体来讲透射率为增大的趋势，其共振峰均发生明显红移，这与式（1）所对应的规律一致，当R增大时谐振腔的共振波长λ也会增加，因此共振峰发生红移现象。如图5（b）所示为圆半径R=270，280，290，300，310，320，330 nm时系统FOM 的取值，对两个Fano 共振的FOM 值总体考虑，可将圆半径R的最优值取为300 nm。

图5 不同圆半径R 对透射率和FOM 的影响Fig.5 Influence of different circle radius R on transmittance and FOM

2.2 Ag 正方形的边长对系统传感性能的影响

当圆半径R=300 nm，拆分距离k=10 nm，耦合距离g=15 nm 时，对谐振腔中Ag 正方形边长a从160 nm 到220 nm 进行参数化扫描，得到Ag 正方形边长a=160，175，190，205，220 nm 时Fano 共振峰透射率曲线如图6（a）所示。可以看出，随着a的增大，两个共振峰均发生红移，这与式（1）所表示的规律一致，因为当Ag 正方形边长a增大时，谐振腔的共振波长也会增加，因此共振峰发生红移现象。随着Ag 正方形边长a的增大，FR1 所对应的透射率几乎不变，而FR2 所对应的透射率整体呈现增加趋势。图6（b）为Ag 正方形边长a=160，175，190，205，220 nm 时系统FOM 的取值，从图中可以看到第一个Fano 共振的FOM 值呈现单调递减趋势，第二个Fano 共振的FOM 值呈现先增大后减小的趋势，所以同时兼顾这两个Fano 共振的FOM 值可以将Ag 正方形边长a的最优值定为190 nm。

图6 不同边长a 对透射率和FOM 的影响Fig.6 Influence of different side length a on transmittance and FOM

2.3 拆分距离对系统传感性能的影响

当圆半径R=300 nm，Ag 正方形边长a=190 nm，耦合距离g=15 nm 时，对拆分距离k从6 nm 至14 nm进行参数化扫描，得到拆分距离k=6，8，10，12，14 nm 时Fano 共振峰透射率曲线如图7（a）所示。可以看出，随着k值的增大，FR1 的位置几乎没有移动，FR2 的位置发生蓝移并且透射率大小几乎不变。因此可以通过调节拆分距离的大小来单独调节第二个Fano 共振的左右移动。图7（b）为拆分距离k=6，7，8，9，10，11，12，13，14 nm 时系统FOM 的取值，综合两种模式来看，可将拆分距离k的最优值定为10 nm。

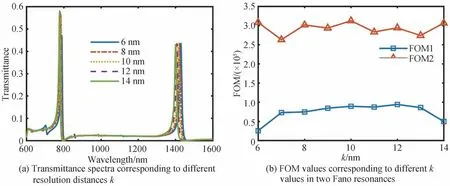
图7 不同拆分距离k 对透射率和FOM 的影响Fig.7 Influence of different resolution distance k on transmittance and FOM

2.4 耦合距离对系统传感性能的影响

当圆半径R=300 nm，Ag 正方形边长a=190 nm，拆分距离k=10 nm 时，对耦合距离g从6 nm 到16 nm进行参数化扫描，得到耦合距离g=10，15，20 nm 时，Fano 共振峰透射率曲线如图8（a）所示，从图中能够得出，随着g值的增大，两个Fano 共振峰的位置几乎没变化，两个共振峰的透射率呈减小的趋势，这时因为耦合距离变小，波导中的能量能够更加容易地耦合进谐振腔内，从而增大谐振腔内的共振能量，因此在出射端口测得的透射率会增大。图8（b）为耦合距离g=6，7，8，9，10，11，12，13，14，15，16 nm 时系统的FOM 值，第一个Fano 共振的FOM 值在6～10 nm 呈增大趋势，10～16 nm 呈减小趋势，第二个Fano 共振的FOM 值在6～11 nm 呈增大趋势，11～16 nm 呈减小趋势，因此综合两种模式来看将耦合距离g定为10 nm。

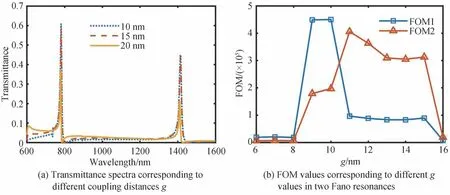
图8 不同耦合距离g 对透射率和FOM 的影响Fig.8 Influence of different coupling distance g on transmittance and FOM

3 系统传感性能分析

对系统结构参数进行优化处理后，综合两个Fano 共振的FOM 值，可将结构参数R=300 nm，a=190 nm，k=10 nm，g=10 nm 定为最优参数，在此参数下，介质折射率n取不同值时，波长与透射率的关系如图9（a）所示。可以看出，随着介质折射率的增大，两个Fano 共振峰均发生红移，透射率峰值均有略微增大。图9（b）为最优参数下，两个Fano 共振的共振波长随介质折射率n的变化图像，可以看到，两个Fano 共振的共振波长与介质折射率均具有良好的线性关系。根据灵敏度计算公式可以计算出第一个Fano 共振的灵敏度S1=800 nm/RIU，第二个Fano 共振的灵敏度S2=1 400 nm/RIU。图9（c）为在最优参数下，该系统的FOM 值与波长的关系，可以看到第一个Fano 共振的FOM 值可高达4.502×105，第二个Fano 共振的FOM值为1.967×105。

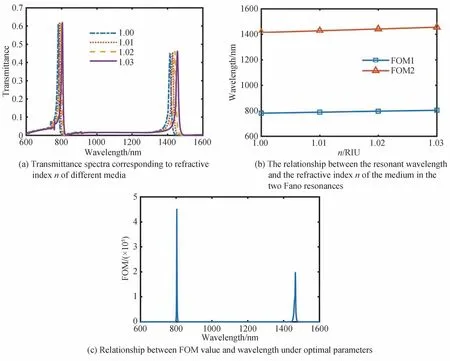
图9 系统传感性能特点Fig.9 System sensing performance characteristics

综上，该结构的几何参数R、a、k、g以及介质折射率都会影响结构的传输性能，通过改变结构几何参数的大小，可以得到系统的最优参数。在最优参数下，该结构表现出良好的传感性能。

4 结论

本文提出了基于单挡板的MDM 直波导侧向耦合谐振腔结构。当入射光以TM 模式进入该结构时，会在金属与介质交界面处激发出SPPs 波，SPPs 波在MDM 直波导传输，当结构中只有金属挡板没有谐振腔，此时结构会产生宽广的连续态谱线，当结构中只有谐振腔没有金属挡板，此时结构会产生较窄的离散态谱线。当连续态与离散态相互干涉时会产生Fano 共振谱线。通过改变几何参数R、a、k、g可以有效调节和优化结构的传感性能，得到R=300 nm，a=190 nm，k=10 nm，g=10 nm 为该结构的最优参数。在最优几何参数下，第一个Fano 共振的灵敏度为800 nm/RIU，对应的FOM 值可高达4.502×105，第二个Fano 共振的灵敏度为1 400 nm/RIU，对应的FOM 值为1.967×105，因此所提出的两种模式的Fano 共振均具有较高的品质因数和灵敏度，同时具有较好的传感性能。该结构可为提高微纳光学传感器的性能提供一种思路。