初中数学课堂情境教学的实践探究

刘红红

《义务教育数学课程标准（2022年版）》明确指出数学学习内容的呈现方式应采用不同的表达形式，这就要求在创设数学问题情境时，要根据具体内容，从学习者已获得的经验入手，利用各种方法创设问题情境，满足学习者多元化的学习需要。

通过对初中数学具体内容以及学生心理特点的分析，可以得知，初中数学内容对于多数学生来说，是比较抽象、枯燥的，因此，要想办法提高学生的学习兴趣。经过研究，在信息技术环境下，创设初中数学问题情境，提出了以下四种策略，分别是创建趣味性的问题情境、创建空间想象的问题情境、创建动态演示的问题情境、创建互动反馈情境。

一、创设趣味性的问题情境

“兴趣是最好的老师”，这就要求教师在课堂教学中，通过合理的方式创设课堂情境，调动学生的积极性，从而激发其求知、探索和实践的愿望。教师设置具有趣味性的教学情境，把学生带入愉快的学习体验中。

如何激发学生的学习兴趣应作为每一位教师必须要优先思考的问题。这就要求教师在进行情境创设时，形式要新颖，内容要生动。这样才能调动学生的学习积极性，学生也可以在求知的过程中得到更积极的情感体验。在信息技术环境下营造的场景，能够使学习者身临其境。学习者通过多姿多彩的场景环境、生动真实的动态演示，达到视听上的多重体验，获得完整的学习感受。

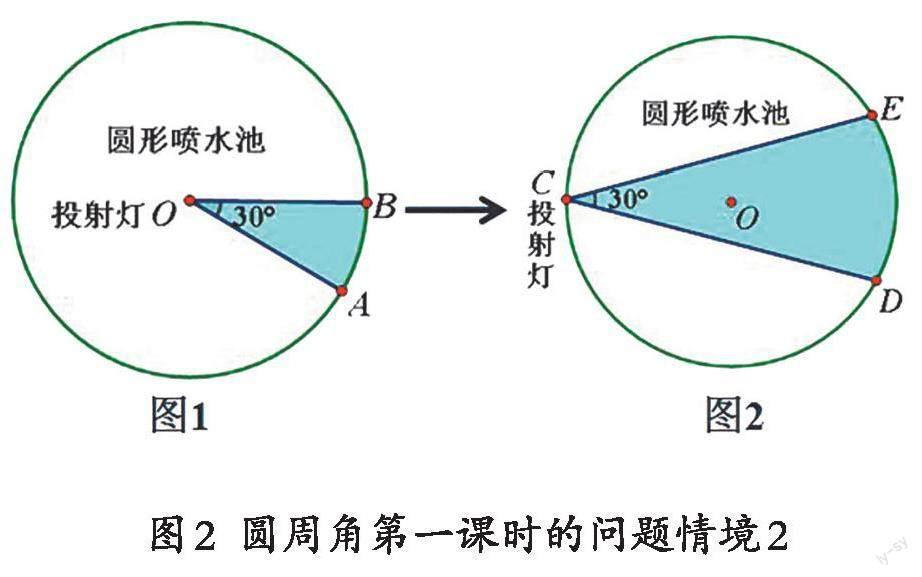
例如：圆周角课题引入。在学习“圆周角”第一课时，做了如下的问题情境：一个喷水池是圆形的，教师聘请学生为设计师，对其进行改造。为美化环境，必须在喷水池内放置彩色投射灯，而每盏投射灯的投射高度为30°（如图1所示），在配置灯具时必须考虑降低成本，也就是使用最少的灯具以实现照亮的目标。请设计者思考，如果要点亮整个水面，至少要安装几盏这样的投射灯？

给出问题后，学生快速找到问题的答案。此时，教师继续提问：大家有没有发现，如果将投射灯的位置变化一下，将投射灯移到该圆形水池的周围（如图2所示），这时请大家思考将要安装的彩色投射灯的数量会不会有所减少？

通过问题串的设计，学生的学习兴趣得到了有效激发。在兴趣的驱使下，学生积极思考，快速融入课堂的问题情境中。学生通过观察、思考、分析、交流、归纳等活动，发现定义圆周角的两个基本要素。教师顺势给出圆周角定义，明确本节课的课题和学习目标。

二、创建空间想象的问题情境

空间观念是《义务教育数学课程标准（2022年版）》中核心素养的主要表现之一。要想更好地达成此目标，教师应为学生创设空间想象的问题情境。

空间思维主要体现在学习者对于一维、二维、三维空间中方向、方位、形状、大小等基本空间概念的理解程度以及对基本几何理论的内化程度等。在学习过程中，要求学习者能想出简单物体的空间位置，还要理解物体的平移、旋转等变化，同时能对抽象的数学式子给予几何意义的解释。传统教学受到传统媒体创设情境的限制，很难创设恰当的教学情境，这对数学教学和学生的学习造成了不利影响。

信息技术环境下，数学知识的展现形式得以完善，能够借助信息平台给数学课程带来多元化的展示形式。

例如：立体图形与平面图形（2）。本节课是在学生学习了平面图形、立体图形的相关概念后，从“视图”的角度感受立体图形与平面图形的相互转化。从不同方向看立体图形、简单几何体的组合图形，从而得到平面图形，这样的观察对象已经变得越来越复杂，使得学生的学习难度越来越大。因此，在创设问题情境时，教师充分利用信息技术，使用人教数字教材的动画演示，呈现更直观、更丰富的素材，为学生的学习创设更丰富的问题情境。

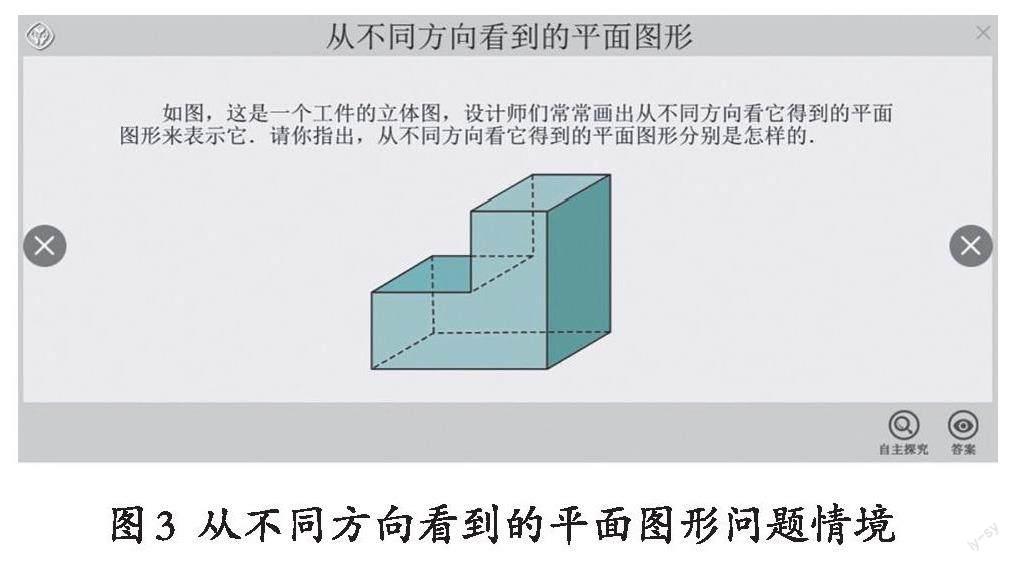
例如：以下是一个工件的立体图形（如图3所示），请同学们思考，我们从不同方向看到的平面图形分别是怎样的？

教师以PPT的形式给出问题和立体图后，可以采用拖拽的方式进行演示，让学生从不同方向观看，帮助学生获得直观的感受。

三、创建动态演示的问题情境

一节精彩的数学课一定包含教师的精彩预设和课堂的动态生成。只有动态的发展才能体现学生思维的生成和发展，让课堂充满活力。动态的演示会让学生的思维在广度和深度上得到发展，有利于学生主体地位的发展。

例如：探索圆周角定理。在探索圆周角定理时，教师提出如下问题（如图4所示），∠ACB是圆周角，请同学们作出AB所对的圆心角∠AOB，请分别测量∠ACB和∠AOB的度数，看看它们之间有什么关系？

在这一过程中，教师指导学生按要求作图，通过所画图形观察并测量角的度数，学生根据度量结果得到∠ACB=  ∠AOB的结论，并用语言进行描述。教师请大家在圆O上再任取一条弧，然后找到这条弧所对的圆心角和圆周角，再进行测量，请大家再次验证所得的结论是否成立。在这一过程中，学生再次经历作图、度量、验证的过程，最终达成共识。

在此学习过程中，教师通过几何画板的动态演示和度量功能，引领学生经历从特殊到一般研究问题的过程，在生动的情境中引导他们去观察、发现和验证同弧所对的圆周角与圆心角之间的关系。

四、创建互动反馈情境

信息技术环境的强大和信息技术设备的不断更新，为我们的课堂带来了新的变化。熟悉的投影机、电子白板、一体机等已经不能再适应现代教学的需要，手机、平板电脑等新型教育方式正进入课堂，为我们带来了教与学的全新感受。依托强大的互动反馈系统，教师实时获得学生反馈的学习信息，并通过及时有效的数据反馈进行分析，及时调整和优化课堂的教学策略，以达到更加理想的课堂教学效果。

例如：在讲授《有理数的乘方》一课时，可利用网络学习系统以提前向学生发布学习任务的方式创設问题情境。要求学生观看微视频，并完成5道客观题，同时完成教师布置的讨论帖内容“从微课的学习中，我的收获和我的困惑”。根据学生在课前任务的完成情况和数据反馈，教师进行二次备课，有针对性地设计教学。

总之，随着信息技术和互联网的飞速发展，新型的教学方式必定会代替传统的教学方式。我们的教学会突破时间和空间的局限，我们的课堂也必然会更加丰富多彩。

（吴  莹）