基于联合加速近端梯度和对数加权核范数最小化的地震数据重建

杨 帆,王长鹏,张春霞,张讲社,熊 登

1.长安大学理学院,西安 710064

2.西安交通大学数学与统计学院,西安 710049

3.东方地球物理公司物探技术研究中心,河北 涿州 072751

0 引言

地震数据重建是地震研究中的一个重要课题,其目的是重建规则采样或不规则采样的缺失痕迹[1]。重建的质量直接影响到后续的处理步骤,如全波形反演[2-3]、偏移矢量倾斜[4]等。人们提出许多不同的方法用于地震数据重建,包括促进稀疏性的L1范数最小化方法、基于预测滤波器的方法、基于压缩感知的方法等,其中:促进稀疏性的L1范数最小化方法要求变换域中的数据通过变换[5-9]稀疏地表示,其局限性是过于注重固定变换中的稀疏表示,所以缺乏对复杂数据的适应能力;基于预测滤波器的方法[10]利用了信号在f-x域(频率-空间域)和f-k域(频率-波数域)的线性可预测性,但是需要等距地震信号数据;基于压缩感知的方法[11-12]利用地震数据的稀疏特征重建地震数据。近年流行的神经网络方法也被应用于地震数据重建[13-17],然而为了获得精确的结果,它需要大量的数据和时间训练网络,以学习输入和输出之间的非线性映射。

低秩矩阵补全方法对数据适应性强,重建效率高,不需要大量的样本来提取数据的特征,且对硬件要求友好,已在地震数据重建方面得到广泛的应用。由于秩函数的非凸性和不连续性,该模型一般是非确定性多项式时间难题(non-deterministic polynomial-time hard, NP-hard),而核范数作为秩函数的凸松弛,在矩阵补全问题中取代了秩函数。这个优化问题可以用奇异值阈值(singular value threshold, SVT)[18]法解决,该算法对特定矩阵的奇异值使用迭代软阈值操作,并使用交替迭代方法求解优化问题,可以有效重建地震数据。低秩矩阵补全问题的另一个模型是核范数正则化线性最小二乘问题,加速近端梯度(accelerated proximal gradient, APG)[19]算法是基于压缩传感的快速迭代收缩阈值算法,可以有效求解该问题。Yang等[20]首次将核范数与地震数据重建联系起来,并通过纹理块算子[21]对地震数据矩阵进行预处理。Zhang等[22]提出基于最大化最小化框架的非凸对数和函数算法(nonconvex log-sum function-based majorization-minimization framework algorithm, LSMM),该算法提出对数和函数代替核范数来逼近矩阵的秩函数。由于对数和函数的非凸性,采用majorization-minimization算法进行求解。Zhang等[23]利用截断核范数正则化重建了地震数据,并用交替方向乘子法(alternating direction method of multipliers,ADMM)进行求解。Wang等[24]首次将加权核范数最小化(weight nuclear norm minimization, WNNM)模型应用于地震数据重建,将L1范数的迭代加权原理扩展到核范数最小化问题中[25-26],取得了较好的效果。然而,权重向量的增加导致一些奇异值在迭代过程中丢失,重建精度也会随之下降。

本文提出基于联合加速近端梯度和对数加权核范数最小化(joint accelerated proximal gradient and log-weighted nuclear norm minimization, APG-LWNNM)的地震数据重建方法。首先通过纹理块算子对原始地震数据进行低秩预处理;然后使用APG算法对低秩地震数据进行初步重建,提出APG-LWNNM算法,使该算法解决优化问题并重建缺失数据,以在迭代过程中减少矩阵奇异值损失,提高重建精度;最后用合成地震数据和真实地震数据对比实验证明APG-LWNNM算法的有效性。

1 纹理块预处理

对于给定的原始数据矩阵X∈Rm×n和纹理块尺寸p,

可以将X分解为mn/p2个子块,标记为Bj∈Rp×p(j∈[1,2,…,mn/p2])。对于分块矩阵:

以B1为例,可以重新组合为

则纹理块矩阵PT(X)可以定义为

PT(X)=[b1,b2,…,bmn/p2]∈Rp2×(mn/p2)。

(1)

式中,PT：Rm×n→Rp2×(mn/p2)表示纹理块算子。相应地,PT′:Rp2×(mn/p2)→Rm×n表示纹理块逆算子。

纹理块矩阵PT(X)具有低秩结构,并且缺失的数据会随机分散在整个矩阵中,避免了全零列的出现。这与低秩矩阵补全理论[18-19]一致。

2 低秩矩阵补全

低秩矩阵补全问题的模型为

(2)

式中:Μ∈Rm×n,为要恢复的矩阵;rank(X)为矩阵X的秩。低秩矩阵补全问题的基本理论是通过问题(2),求得最优的低秩矩阵X*,使得X*在已知项上的元素与M足够接近,在未知项上的元素即为恢复的缺失值[27]。

2.1 核范数最小化

由于秩函数的非凸性和不连续性,直接求解问题(2)是NP-hard的。核范数是矩阵单位球上rank(X)的凸近似,常用来近似rank(X),则问题(2)可转化为

(3)

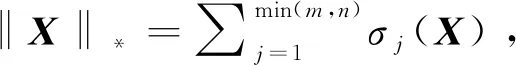
由于核范数不能对rank(X)产生很好的近似,Gaiffas等[25]将迭代加权原理应用到了核范数中,提出了加权核范数来逼近rank(X):

(4)

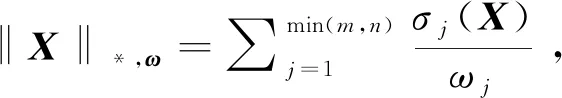
2.2 核范数正则化线性最小二乘

低秩矩阵补全问题的另一个模型是核范数正则化线性最小二乘问题。该正则化问题是无约束非光滑凸优化问题的一种特殊情况,其目标函数是核范数和具有Lipschitz连续梯度的凸光滑函数之和,即

(5)

式中:λ>0,为超参数;‖·‖2为矩阵的谱范数。APG算法[19]可以有效地求解核范数正则化线性最小二乘问题,它结合了梯度下降法和近端算子,在每次迭代中,通过计算当前矩阵的梯度和近端算子来更新矩阵的近似解,其中,近端算子可以有效地对矩阵进行低秩约束,从而得到更加合理的解。

3 APG-LWNNM算法

3.1 LWNNM算法

LWNNM算法目标函数为

(6)

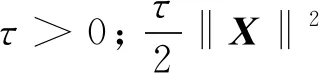
将X的奇异值分解记为X=UΣVT,其中:

U=[u1,u2,…,ur];

V=[v1,v2…,vr];

Σ=diag(σ1,σ2,…,σr)。

由

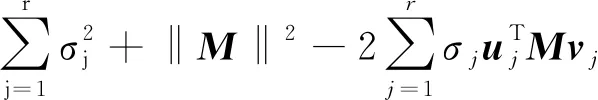
(7)

(式中,〈·,·〉为矩阵的内积运算),此时固定M,只考虑X,结合式(7),则式(6)的目标函数可转化为

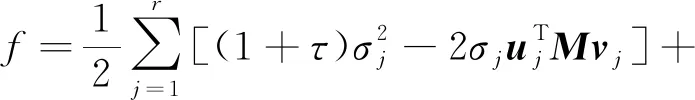
(8)

将M的奇异值分解记为M=U′Σ′V′T,其中:

式(8)可转换为

(9)

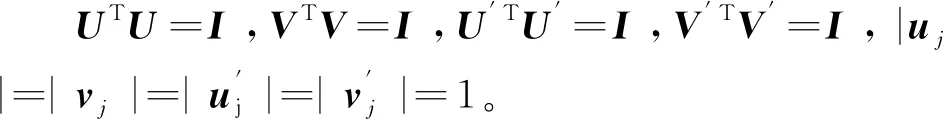
(10)

固定j,则目标函数为

(11)

此时式(11)易求解。当

时,目标函数取得最小值。

综上所述,式(6)可通过对数加权软阈值算子求得唯一解:

(12)

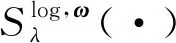
(13)

(14)

其中,

(15)

由此可知,对数权重向量的引入减少了矩阵奇异值的损失,保留了更多的信息量。

3.2 APG-LWNNM算法

本文提出的APG-LWNNM算法基于低秩矩阵补全理论,主要分为四阶段进行。第一阶段用纹理块算子对输入数据进行低秩预处理;第二阶段用APG算法求得初步重建结果;第三阶段用本文所提LWNNM算法解决优化问题并重建地震数据;最后用纹理块逆算子进行逆处理。

具体流程如图1所示。

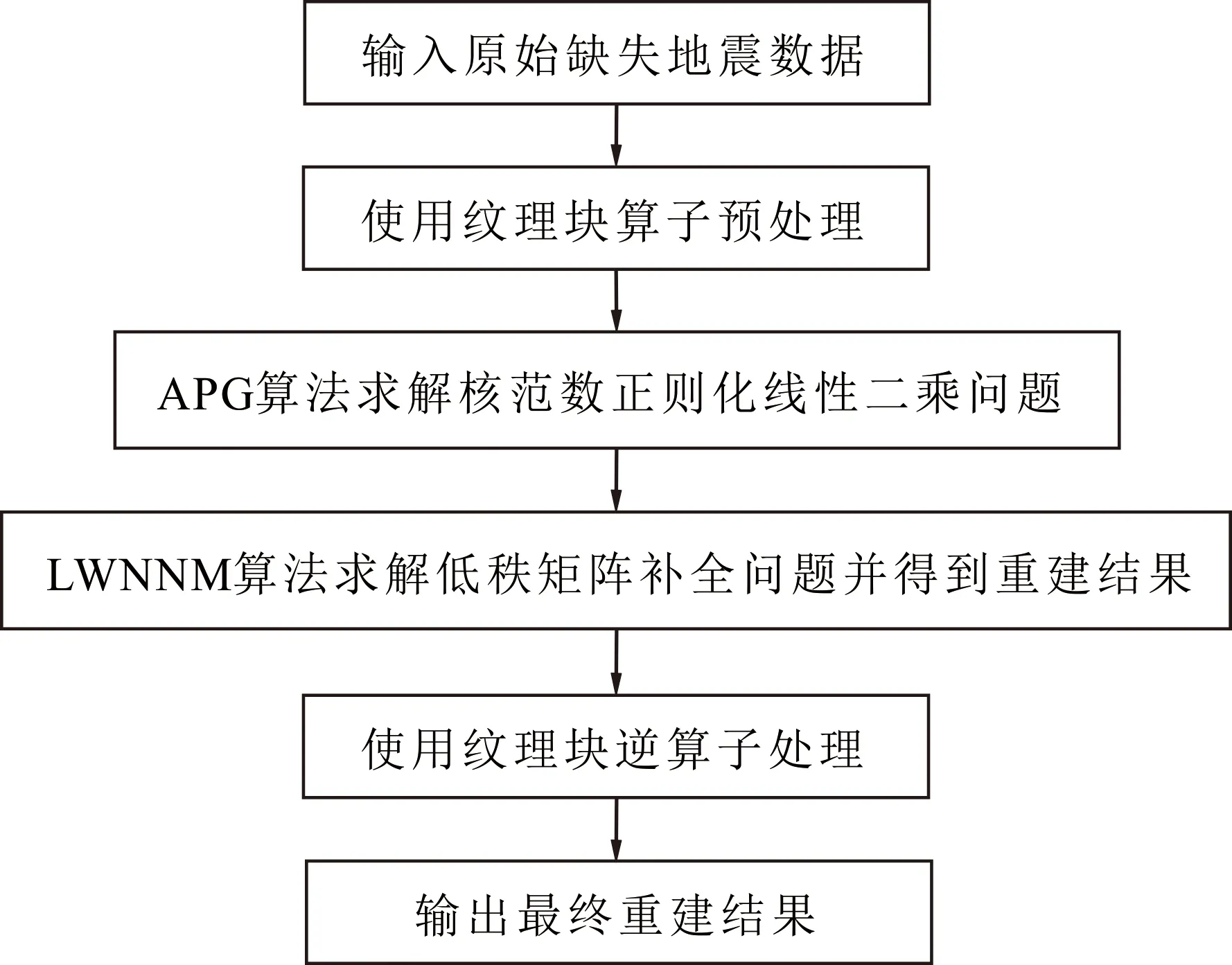
图1 APG-LWNNM算法流程图

aPG-LWNNM算法如下。

输入:缺失地震数据M,k,τ,λ,tol,λtar;

计算:1)纹理块矩阵PT(Μ);

2)通过APG算法得到X;

赋值:ω=σ(X);

Whileλ>λtar

θ=∞;

Whileθ>tol

Xold=X;

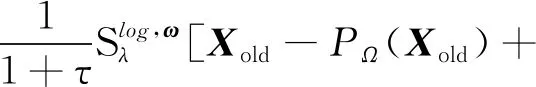
PΩ(M)];

θ=‖X-Xold‖/‖Xold‖;

end

赋值:ω=σ(X),λ=k×λ;

End

输出:纹理块逆矩阵PT′(X)。

其中:k=0.02;tol=10-3;λ=1;λtar=10-4·‖PT(M)‖;τ<10-6,否则容易求得局部最优解。具体实验参数依输入地震数据而定。

4 实验与分析

本文以信噪比和重建误差为评价指标。信噪比的概念来源于电子通信,代表信号和噪声的有效功率之比。在插值方法中,将原始数据和重建结果之间的差距视为噪声,噪声越大说明重建精度越低。信噪比本质上为相对误差,重建误差本质上为绝对误差。信噪比表示为

(16)

重建误差表示为

e=‖X-X*‖2。

(17)

式中:X为原始地震数据;X*为重建结果。信噪比数值越大、重建误差数值越小,表明重建越度越高。

4.1 消融实验

选取一组地震数据共300道,300个采样点,采样间隔为0.004 s,并对该数据进行随机缺失,缺失率为20%～80%。分别使用APG-LWNNM算法和LWNNM算法进行数据重建,重建结果的信噪比和重建误差见表1。

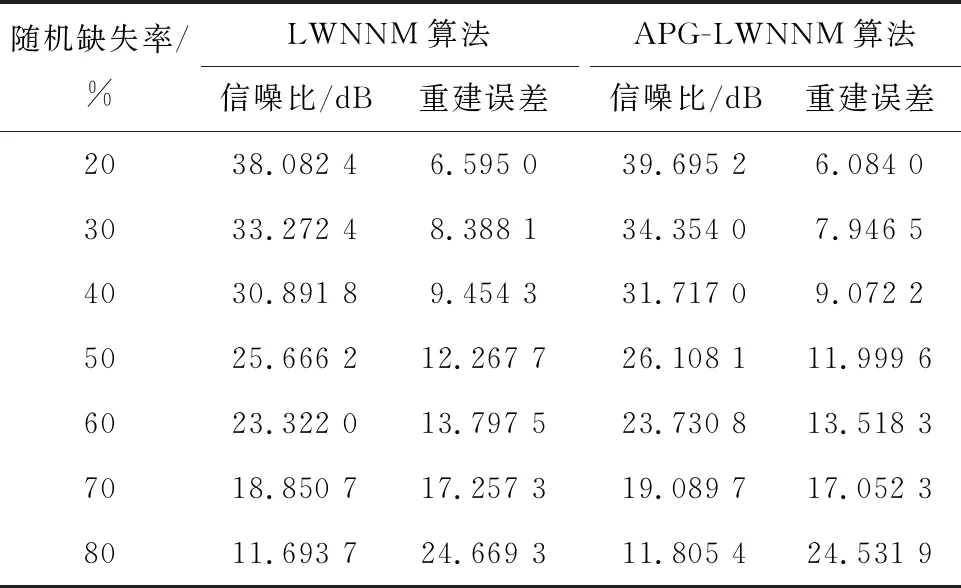
表1 APG-LWNNM算法与LWNNM算法的重建性能比较

由表1可见,在同组数据相同缺失率条件下,APG-LWNNM算法的重建结果信噪比更高,重建误差更低,即重建精度更高。因此,使用APG算法求得初步重建结果是必要的。

4.2 实验结果与分析

为评估APG-LWNNM算法的有效性,本节将在合成地震数据和真实地震数据上进行实验,并与现有主流的低秩地震数据重建算法SVT、WNNM以及LSMM进行比较,按原算法进行参数设置。

合成地震数据(图2a)共260道,300个采样点,采样间隔为0.004 s。对随机缺失40%地震道数据(图2b),分别用SVT、WNNM、LSMM和本文所提APG-LWNNM等4种算法进行重建。可以看出:SVT算法(图2c)对部分缺失数据未完全重建;WNNM算法(图2d)和LSMM算法(图2e)重建结果较好,但对数据细节的恢复不够完备,仍有部分数据无法恢复;APG-LWNNM算法(图2f)对该缺失数据能够较好地恢复,数据细节恢复更完备,生成的纹理更加丰富。

上述4种算法在该数据上重建结果的信噪比和重建误差见表2。其中APG-LWNNM算法重建结果的信噪比最高,重建误差最低。

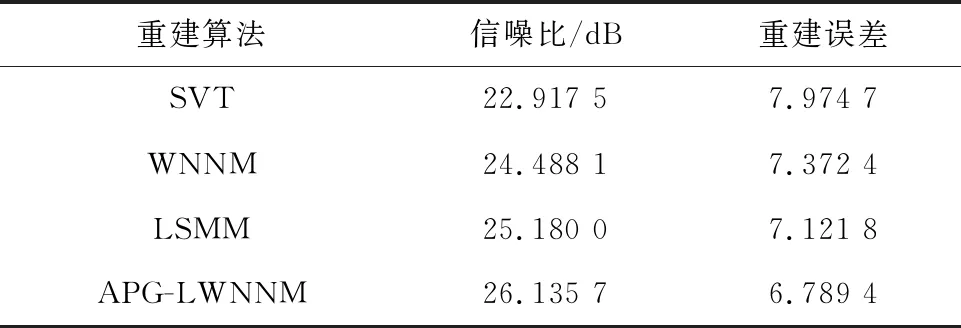
表2 合成地震数据重建性能比较

为了更加直观地对重建结果进行比较,对第162道地震数据重建结果进行单道比较。SVT、WNNM、LSMM和APG-LWNNM等4种算法重建结果单道比较结果(图3a—d)以及相应的残差(图3e—h)表明,APG-LWNNM算法的重建结果更好。

本文在Mobil Avo Viking Graben Line 12叠前真实数据集和Netherlands F3真实数据集上评估APG-LWNNM方法。

Mobil Avo Viking Graben Line 12叠前地震数据集是一个二维野外数据集,包含北海的1 001个炮点集。每个炮点集有120道,均匀分布,距离为25 m。每道地震数据有1 500个时间采样点,采样间隔为0.004 s。用于实验的数据大小为120×300。

Netherlands F3地震数据集是一个位于荷兰近海的小型海洋野外地震数据集,包含601个炮点集。每个炮点集有951道,每道地震数据有463个时间采样点,采样间隔为0.004 s。用于实验的数据大小为200×180。

Mobil Avo Viking Graben Line 12和Netherlands F3地震数据集下载地址为https://wiki.seg.org/wiki/,所有数据均可为公众使用。

首先对Mobil Avo Viking Graben Line 12叠前地震数据(图4a)进行30%地震道随机缺失(图4b),分别使用SVT、WNNM、LSMM以及APG-LWNNM等4种算法对缺失数据进行重建,可以看出:SVT算法(图4c)不能很好地重建缺失数据,纹理模糊;WNNM算法(图4d)和LSMM算法(图4e)重建结果一般,纹理不够丰富;而APG-LWNNM算法(图4f)重建结果生成的纹理较丰富。特别是在矩形框内,APG-LWNNM算法重建结果更符合原始数据。

4种算法在Mobil Avo Viking Graben Line 12叠前地震数据上重建结果的信噪比和重建误差见表3,其中本文所提APG-LWNNM算法的信噪比最高,重建误差最低。

为了直观地比较比较重建结果,接下来用评价指标对单个地震道作进一步分析。将SVT、WNNM、LSMM和APG-LWNNM等4种算法重建结果第2道进行单道比较,由重建结果(图5a—d)及相应的残差(图5e—h)明显看出,APG-LWNNM算法的重建结果更接近于原始地震数据,与原始数据残差最小,表明APG-LWNNM算法的重建精度优于其他3种算法。

接着选取Netherlands F3地震数据集(图6a)共200道,180个采样点,采样间隔为0.004 s。随机缺失比例为60%(图6b),分别使用SVT、WNNM、LSMM以及APG-LWNNM等4种算法对缺失数据(图6b)进行重建(图6c—f), 其信噪比和重建误差见表4,第59道地震数据单道比较及相应的残差见图7。

表4 Netherlands F3地震数据重建性能比较

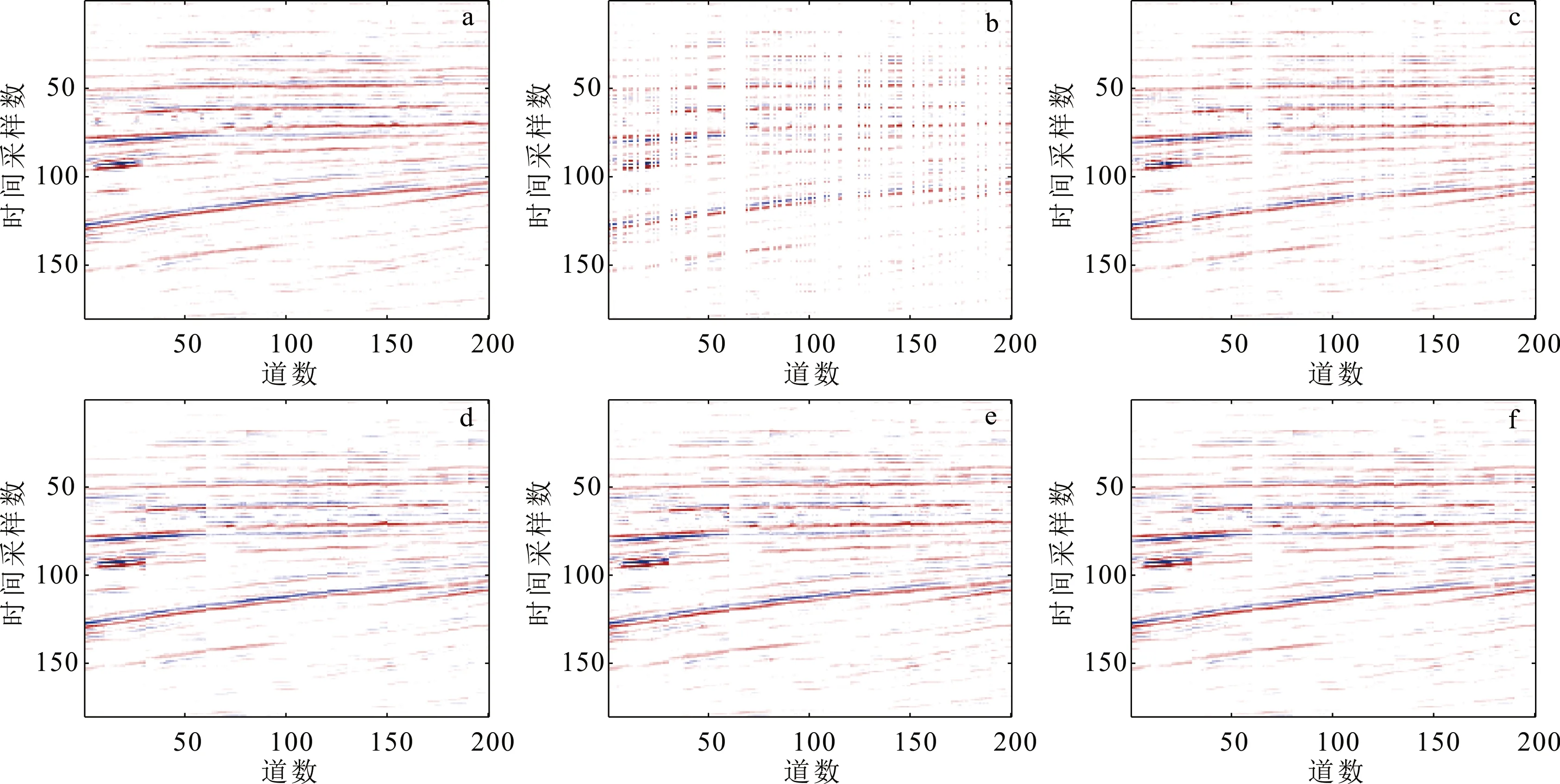
a. 原始真实地震数据;b. 随机缺失60%真实地震数据;c. SVT算法重建结果;d. WNNM算法重建结果;e. LSMM算法重建结果;f. APG-LWNNM算法重建结果。

a. SVT算法重建结果;b. WNNM算法重建结果;c. LSMM算法重建结果;d. APG-LWNNM算法重建结果;e. SVT算法残差;f. WNNM算法残差;g. LSMM算法残差;h. APG-LWNNM算法残差。

结合表4、图6和图7可以分析得到:SVT算法重建结果仍有部分地震道残缺,且单道图与原始数据有明显误差,欠理想;WNNM算法和LSMM算法结果较好,但其信噪比较低,重建误差较大;APG-LWNNM算法能够较完整地重建该缺失数据,且其信噪比最高,重建误差最低。由第59道地震数据单道比较可知,APG-LWNNM算法的重建结果(图7d)与原始数据更接近,振幅差值(图7h)最小,进一步表明APG-LWNNM方法的重建精度更高。

5 结论与建议

本文提出基于APG-LWNNM的地震数据重建方法,主要原理为低秩矩阵补全理论,得到如下结论:

1)APG-LWNNM算法重建结果精度高。在迭代过程中,对数权重向量的引入减少了数据矩阵奇异值的损失,尽可能保留了矩阵的信息量。APG-LWNNM算法的重建结果生成了更丰富的纹理,并且获得了最高的信噪比和最低的重建误差,在定性和定量分析上均有提升。

2)APG-LWNNM算法重建效率高。与深度学习方法相比,低秩矩阵补全方法无需学习地震数据特征拟合网络参数,可以加快数据重建速度,对硬件要求更友好。

3)APG-LWNNM算法对地震数据适应性强。与深度学习方法相比,低秩矩阵补全方法可以对缺失地震数据直接重建,不需要大量的数据样本训练多个隐藏层的网络。

低秩性是低秩矩阵补全理论的前提,并且奇异值表示了矩阵的信息量。因此,后期研究方向是如何更高效地低秩预处理地震数据和如何在迭代过程中更多地保留矩阵奇异值。