5种排水条件下饱和重塑黄土三轴剪切特性

刘 鑫,苗雪青,黄 良,魏 骁

1.长安大学地质工程与测绘学院,西安 710064

2.浙江大学建筑工程学院,杭州 310058

0 引言

黄土工程中由渗流引发的灾害普遍而严重,其表现为土体的变形和失稳,而根源在于黄土内部独特的强度衰减[1-5]。因此,研究在渗流作用下饱和黄土的剪切特性对揭示黄土工程渗流灾变机制至关重要。

针对土体在渗流作用下的剪切破坏问题,前人多采用砂土进行研究。如:Chu等[6]采用应变增量比ξ(ξ为试样在三轴试验过程中体应变率与轴应变率的比值)控制三轴试验中试样的排水(吸水)条件,研究发现饱和砂土的渐近状态与排水条件关系密切,并建立了渐近状态应力比(偏应力q与平均有效应力p′的比值)和应变增量比的函数关系;路德春等[7]认为饱和砂土自身的剪胀特性和排水边界共同决定了砂土剪胀性的发挥程度,进而影响其内摩擦角的发挥;张建民等[8]发现饱和砂土在振动至液化状态后再进行单调剪切,呈现吸水、剪胀的趋势,在自由吸水或强制吸水条件下剪切,饱和砂土会产生具有流动特征的大变形。此外,Ladd[9]用实例表明,采用完全排水条件下土体的抗剪强度会高估土质斜坡的稳定性,而采用不排水强度分析得出的稳定性系数往往偏低,对于同一种工况,上述两种分析方法的结果可能相差一倍以上;由此可见,渗流条件对分析结果的影响极大。与砂土相比,黄土具有层次多、级配广等特点[10-12],其渗流条件更复杂多变[13-15]。综上来看,采用常规三轴排水剪切和不排水剪切试验分析黄土边坡的渗流情况是不全面的。

然而,文献中有关黄土在不同渗流条件下剪切破坏的研究十分有限,且多为数值模型分析而非试验研究[16-19]。如:李萍等[20]模拟天然降雨条件,研究了黄土-古土壤层中水分的入渗规律,发现浅层黄土受蒸发控制,而深层饱和黄土以水汽迁移为主;蔡国庆等[21]采用一维土柱试验研究了砂质黄土在有竖向荷载条件下的湿化过程;谌文武等[22]模拟了渗透持时对黄土渗透系数的影响。但上述研究均没有考虑剪切力和渗流的耦合作用,因此无法揭示黄土渗流剪切破坏的机制。值得注意的是,张林等[23]开展了饱和黄土不同排水条件下的三轴试验,但试验仅控制了4种排水条件,且没有考虑试样密度的影响。可见,当前对饱和黄土渗流剪切特性的研究仍不足,对其影响下灾变机制的认识仍然不清。

1 试验材料和方案

1.1 试验材料和试样制备

试验材料取自陕西省延安市某治沟造地工程一处黄土高填方边坡。依照《土工试验方法标准》(GB/T 50123—2019)[24]对黄土进行水筛法和密度计法试验,结果表明试样的黏粒(粒径<5 μm)质量分数为10.5%,粉粒(粒径5～75 μm)质量分数为83.2%,砂粒(粒径>75 μm)质量分数为6.3%。黄土的其他物理指标见表1。

表1 重塑黄土基本物理指标

将野外取回的黄土经过烘干,过筛,加水,配至11.6%的目标含水率,并闷土24 h后采用湿法制备试样[25-26]。如图1所示,首先根据试样的目标孔隙比,称取湿土的总质量;然后分5层装入击实器逐层击实,每层击实完成后对表面进行刮毛处理,使层间土接触良好;最后制成直径为50 mm、高度为100 mm的圆柱形试样。制样完成后装入三轴仪,对其进行饱和:首先采用二氧化碳和无气水依次通过试样;然后分级饱和至围压330 kPa、反压300 kPa,在增大各级反压前,测试试样的孔压系数(B),当B≥0.95时,黄土三轴试样为饱和状态[27];最后,待试样饱和完成后,对其进行有效固结应力为100 kPa的均压固结。

a. 步骤①,配置目标含水率土样;b. 步骤②,取适量湿土,分层加入制样器;c. 步骤③,击实至目标高度并刮毛表面;d. 步骤④,制样完成,拆除模具。

1.2 试验方法

试验采取Chu等[6]提出的应变增量比(ξ)控制试样的排水(吸水)条件。在充分总结野外调查成果并结合前人研究的基础上,将黄土边坡的渗流条件大致概括为不排水(ξ=0)、自由排水(ξ=ξCD)、强制排水(ξ>ξCD)、部分排水(0<ξ<ξCD)、强制吸水(ξ<0)5种情况,其中ξCD为黄土试样在排水剪切(CD)条件下应变增量比的实测值,具体描述如表2所示。

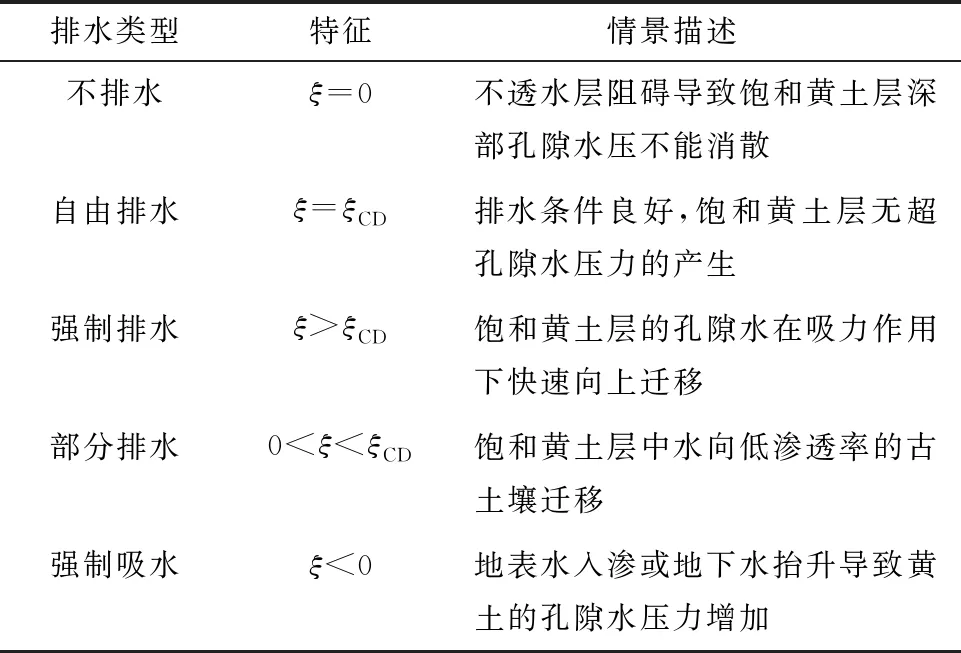
表2 饱和黄土渗流类型总结

通过设置VJ Tech三轴仪的反压控制器和位移传感器(LVDT)实现不同应变增量比条件下的三轴试验(图2a)。本次试验在剪切过程中采用的轴应变率为0.05%/min,所有试验均采用相同的轴应变率进行剪切,以排除轴向加载速率对试验结果的影响。需要注意的是,在自由排水条件下,试样以该轴应变率剪切时没有超孔隙水压力的产生。试验步骤如图2b所示,首先在试验前根据ξ计算出对应的体应变率(dεv/dt),该值与试样固结后体积(Vc)的乘积(Vcdεv/dt)即为试样的体变速率(ΔV),也就是单位时间内试样的排水(吸水)体积。然后,在试验中通过体变仪来控制试样的体变速率(表3)。图3为不同应变增量比条件下黄土试样的体应变(εv)与轴应变(εa)关系图,图3中直线的斜率为应变增量比的实际测量值εm。从表3可以看出,应变增量比与实测值十分接近,表明三轴仪控制的效果良好。

①轴力传感器;②位移传感器;③围压控制器;④反压控制器;⑤孔压传感器;⑥试样。

a. 孔隙比较大试样;b. 孔隙比较小试样。图中各试样直线斜率为ξm。ξ和ξm的值见表3。

表3 不同排水条件下试验方案

本次试验完成了2组孔隙比、5种排水条件共计12组试验,具体方案见表3,试验编号前缀“L”表示孔隙比较大试样,“M”表示孔隙比较小试样。为了达到渐近状态,本次试验控制试样εa>20%作为试验的终止标准。同时,考虑加载过程中试样截面积发生改变,在计算偏应力时,根据《土工试验方法标准》(GB/T 50123—2019)[24]中的固结排水剪切校正公式对试样的剪切面积进行了修正。

2 试验结果分析

2.1 孔隙比对饱和重塑黄土剪切特性的影响

孔隙比是研究土体剪切特性不可忽视的重要因素。图4对比了两种孔隙比的黄土试样在自由排水条件下的试验结果。由图4a可以发现,重塑黄土试样在剪切过程中均表现出应变硬化,且孔隙比较小试样(M-4)应变硬化的趋势更明显。与图3的规律不同,图4b中黄土试样的体应变随着轴应变的增大,先快速增大后增长速率变慢,应变增量比(即斜率)不恒定。为了方便对比,取平均体应变率与平均轴应变率的比值作为自由排水条件下的应变增量比(ξCD),计算得到试样L-4的应变增量比为0.130 0,试样M-4的应变增量比为0.080 0(表3)。对比以上两组试样不难发现,对于孔隙比较小,即更密实的黄土试样(M-4),其应变增量比也较小。

a. 应力-应变曲线;b. εv与εa关系图。

依据由图4b计算得到的ξCD可以判断,当ξ=0.03时,两种孔隙比试样均为部分排水的情况。如图5所示,试样L-1和M-1的剪切特性有明显的区别:首先,M-1试样在有效应力路径图(图5a)上出现拐点,表明该试样在剪切过程中由剪胀状态过渡到剪缩状态;另外,两个试样在剪切过程中均表现为应变软化趋势,但M-1试样的峰值强度和残余强度比L-1更高(图5b)。

2.2 两组hs-CRP与血嗜酸粒细胞水平比较 治疗后，两组患者hs-CRP与血嗜酸粒细胞水平较治疗前明显降低，且B组均低于A组，差异均有统计学意义(P<0.05)。见表1。

a. 有效应力路径曲线;b. 应力-应变曲线。

图6为黄土试样L-5和M-2在强制吸水条件下的试验结果。一方面,从有效应力路径(图6a)可以看出,虽然L-5和M-2试样的平均有效应力都减小,但M-2试样出现了明显的拐点,这和图5a中试样M-1的曲线特征类似,表明在部分排水和强制吸水条件下,饱和重塑黄土试样的剪胀性随着孔隙比的减小而增强;另一方面, L-5和M-2试样均表现为应变软化趋势,且试样M-2的峰值强度更高,而残余强度则比较接近(图6b)。

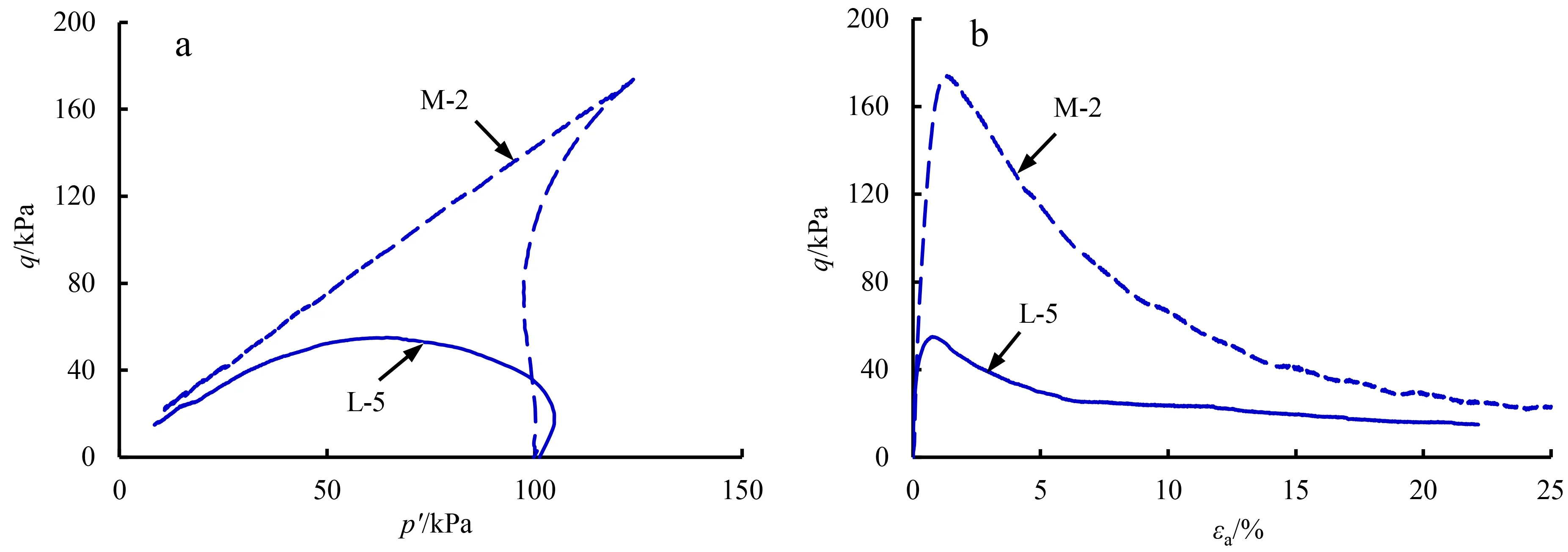
a. 有效应力路径曲线;b. 应力-应变曲线。

图7为黄土试样L-3和M-3在强制排水条件下的试验结果。与图5a和图6a相比,图7a中孔隙比对试样有效应力路径的影响并不明显;由图7b可知,试样均表现出强烈的应变硬化,且较小孔隙比的试样(M-3)具有更高的剪切强度。

a. 有效应力路径曲线;b. 应力-应变曲线。

2.2 排水条件对饱和重塑黄土剪切特性的影响

图8和图9对比了特定排水条件下黄土试样的剪切特性。图8为重塑黄土试样(L-2,3,4)在ξm>0条件下的三轴试验结果。从广义上讲,在自由排水条件( L-4)下黄土试样的剪胀性可以自由发挥,而在强制排水条件(L-3)下其剪胀性受到抑制。在这两种情况下,试样表现为随平均有效应力增大呈硬化趋势,且随着应变增量比增加,试样L-3比L-4的偏应力高,硬化趋势更明显。

a. 有效应力路径曲线;b. 应力-应变曲线;c. 超孔压-应变曲线 。Δu为超孔隙水压力。

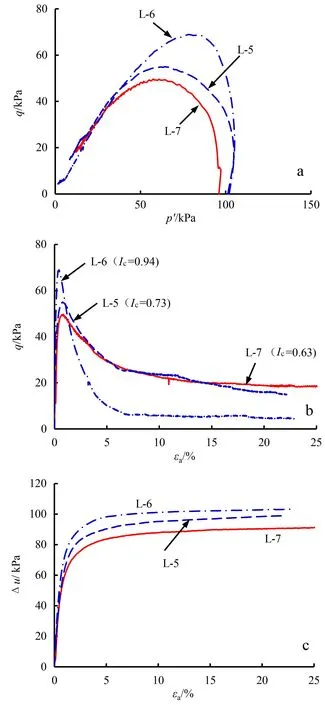
a. 有效应力路径曲线;b. 应力-应变曲线;c. 超孔压-应变曲线。Ic为坍塌度指数。

此外,在部分排水条件下剪切,试样L-2出现了从应变软化到硬化的过渡状态[28],其相变发生的位置被标记为点A。图8a中,与该试样剪切的起点(100,0)相比,A点的平均有效应力(p′)减小,说明试样发生剪缩;在A点之后,p′持续增大,试样表现为剪胀。从图8b中可以看出,L-3与L-4试样均表现出应变硬化趋势,而L-2试样则表现为先软化后硬化的趋势。其次,L-4试样的峰值强度大于L-2的峰值强度。应变增量比会影响超孔隙水压力的累积规律(图8c),从而改变黄土试样在剪切过程中的有效应力路径。比如,在部分排水条件下,试样发生软化是由于超孔隙水压力增大,而平均有效应力减小;在强制排水条件下,剪切后期的超孔隙水压力为负值,则试样的硬化趋势更强烈。

如图9a所示,当ξm≤0时,试样L-5和L-6在剪切过程中吸水,剪胀性被强制发挥[8],在试验中表现为平均有效应力减小,试样呈软化趋势。与不排水条件(L-7)相比,试样在强制吸水条件(L-5,6)下的峰值强度(qpeak)更高,且吸水程度越大,qpeak值越高;这与文献中关于砂土的趋势相反,如Chu等[6]和路德春等[7]研究发现,Sydney砂、北京砂的峰值强度随着吸水程度增大而降低(图10)。

a. Sydney砂[6], e=0.599～0.621, emin=0.565, emax=0.855;b.北京砂[7], e=0.620, emin=0.580, emax=0.850。 e、emin、emax分别为试样的实际孔隙比、最小孔隙比、最大孔隙比。

图9b为试样的应力-应变曲线,偏应力在轴变为1.5%左右时迅速增加至峰值强度,之后逐渐减小。试样的吸水程度越大,则接近残余强度时的轴应变越小,试样表现出越强的软化特征。为了更好地描述试样的软化程度,本文引入坍塌度指数Ic,其定义[29]如下:

Ic=(qpeak-qcs)/qpeak。

(1)

式中:qcs为终止轴向应变处的偏应力;qpeak为对应的峰值强度。当Ic=0时,试样无应变软化发生。由图9b可知,Ic随着应变增量比的减小而增大;表明黄土试样在强制吸水条件下的软化程度大,失稳后的残余强度低,更容易发生具有大变形特征的流滑。

图9c给出了试验过程中超孔压的发展规律,随着吸水程度的增大,超孔隙水压力的稳定值也增大,整个曲线呈近似双曲线形状,并逐渐接近于有效围压值。

3 黄土渐近状态与剪胀性分析

由前文可知,在三轴试验中,可通过应变增量比来控制试样的排水条件,而排水条件对重塑黄土的剪切特性有显著的影响。针对饱和重塑黄土在不同排水条件下的应力路径特点,量化分析了重塑黄土的渐近状态、剪胀性与应变增量比的关系。

3.1 黄土渐近状态和应变增量比

渐近状态是由Gudehus等[30]在饱和砂土三轴剪切试验中首次提出的:在进行常应变增量比加载时,发现有效应力路径逼近于一条与初始应力状态无关的直线,称之为渐近状态。图11汇总了黄土试样在不同排水条件下的有效应力路径,图中直线的斜率为不同排水条件下的渐近状态应力比(η)。

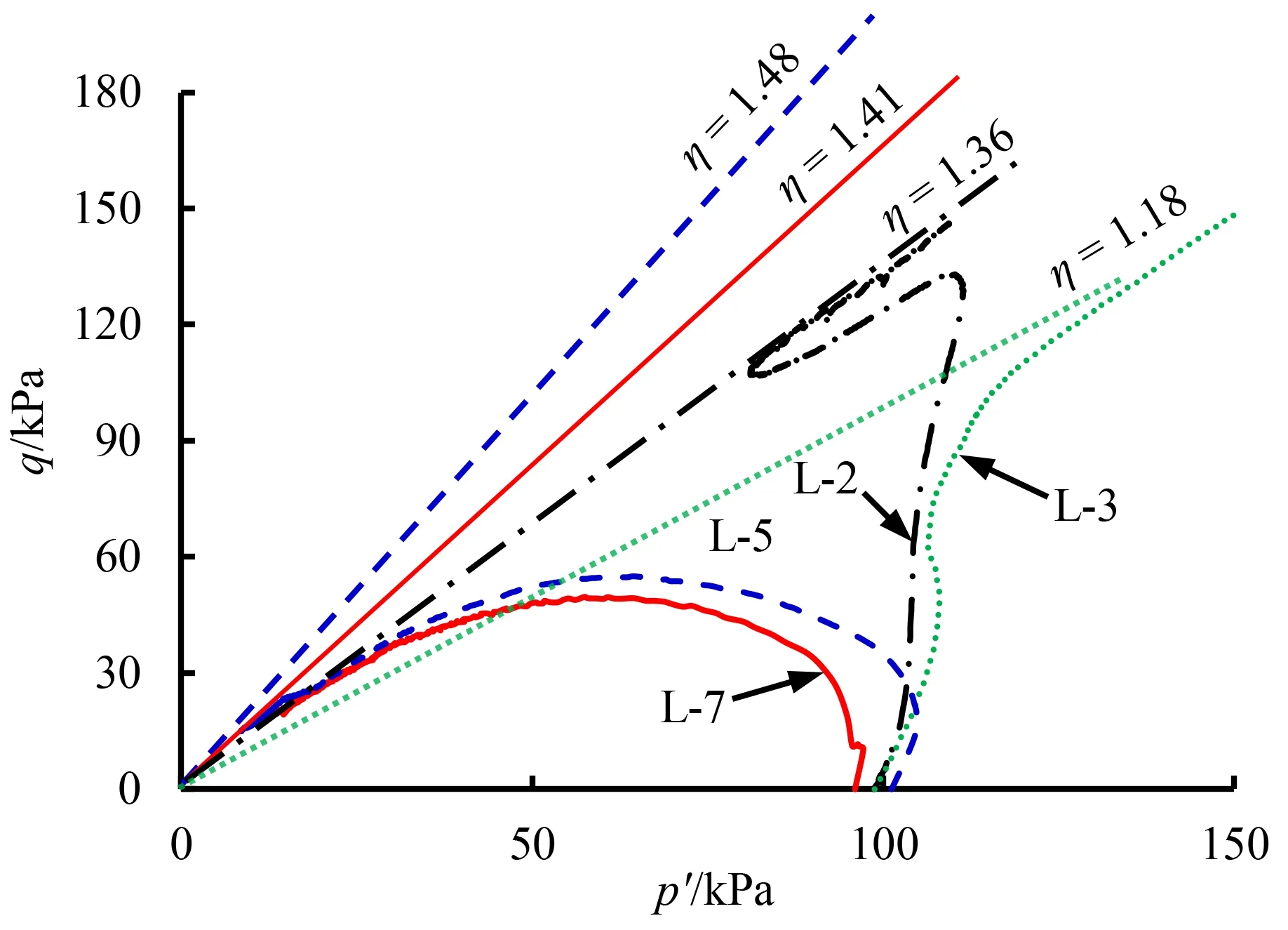
η. 渐近状态应力比。

从图11可以看出,应力比和应变增量比呈负相关关系。Chu等[31-32]和Lo等[33]在大量的砂土试验中也观察到了类似的现象,并建立了二者的函数:

ξ=3(η0-η)/η0。

(2)

式中,η0为不排水条件下的渐近状态应力比。以图11为例,将本次试验的数据(ξ和η)进行拟合,可得到一条相关度R2=0.96的直线,其表达式为

η=-0.47ξ+1.41 。

(3)

式(3)为式(2)的另一种表达形式,即式(2)中η0=1.41,这表明部分排水(吸水)条件下的饱和重塑黄土渐近状态规律也符合式(2)。渐近状态应力比是分析土体强度的重要参数,反映了土体内摩擦角的实际发挥程度。由图11可知,在持续剪切荷载作用下,当应变增量比降低时,饱和重塑黄土的渐近应力比增大,即有效发挥的内摩擦角增加。

3.2 黄土剪胀性和应变增量比

广义的剪胀性指剪切引起的体积变化,包括了“剪胀”和“剪缩”。本次试验通过设置应变增量比,控制了试样的排水条件,使黄土试样在剪切时的剪胀性被抑制或被强制发挥,因此试样剪胀性的发挥程度必然与应变增量比有关。通常土体的剪胀性(d)也可以通过剪胀方程[34-36]来描述:

(4)

(5)

式中:dεa为轴应变增量;dεr为径向应变增量。假设在渐近状态时,不同排水条件下的弹性应变增量对黄土试样剪胀性的贡献远小于塑性应变增量,认为塑性应变增量与总应变增量相等,联立式(4)(5),并代入ξ=dεv/dεa可得

d=dεv/dεd=3ξ/(3-ξ) 。

(6)

当试样排水时,由于体应变增量为正值,则剪应变增量始终为正值。根据式(6),试样在排水时,d>0。反之,当试样吸水时,d<0。

进一步联立式(3)(6),可得

η=3η0/(3+d) 。

(7)

由式(7)可知,重塑黄土试样的η与d呈负相关关系。当试样排水程度越大(d>0),试样的剪胀性越容易被抑制,η值降低,表现为土体内摩擦角的发挥程度低;而当试样吸水程度越大(d<0),此时试样的剪胀性越容易发挥,η值变高,说明土体内摩擦角发挥的程度更高。

4 结论

1)在不排水和强制吸水条件下,黄土试样表现为应变软化趋势;在自由排水和强制排水条件下,试样均表现出应变硬化趋势;在部分排水条件下,试样为应变软化或应变软化到硬化的过渡状态。

2)本文引入坍塌度指数来描述试样的软化程度,发现试样的坍塌度指数随着应变增量比的增大而减小,说明黄土试样的软化程度随着应变增量比的减小而增大,即黄土在强制吸水条件下更容易发生失稳。

3)试样L-4的应变增量比为0.130 0,试样M-4的应变增量比为0.080 0,表明试样在自由排水条件下的应变增量比与孔隙比有关。此外,改变试样的孔隙比会影响峰值强度,在强制吸水和部分排水条件下还会影响有效应力路径。

4)基于渐近状态方程和剪胀方程,分析了饱和重塑黄土的渐近状态和剪胀性,验证了渐近状态方程在黄土中的适用性,发现黄土试样的渐近状态应力比与剪胀性呈负相关关系,表明渗流条件与剪胀性的发挥程度密切相关。