基于CV-XGBoost的水下分流河道砂体厚度预测及应用

白青林,刘烜良,张军华,王福金,刘中伟,焦红岩

1.中国石化胜利油田分公司现河采油厂,山东 东营 257068

2.中国石油大学(华东)地球科学与技术学院,山东 青岛 266580

0 引言

水下分流河道是一类广泛分布的沉积储层。由于河道宽度小,叠置、交叉严重,垂向厚度薄、互层多,均方根振幅等常用地震属性中没有明显的河道特征,其精细描述与储层厚度预测都有很大的困难。

以往有研究人员[1]利用地层厚度与砂地比的乘积来估算砂体厚度,前提是砂体分布与沉积比较稳定。也有研究人员[2]用多井交会分析的方法来预测厚度,但其精度受井震相关性的限制。还有不少学者将机器学习方法用于砂体厚度预测,如随机森林回归(random forest regression, RFR)[3]、支持向量回归(support vector regression, SVR)[4]、混合密度网络预测[5]等,取得了一定的地质效果,但其应用对象比较简单。

本文以胜利油田通61井区水下分流河道储层为例,研究了基于极限梯度提升(extreme gradient boosting, XGBoost)的砂体厚度预测方法。通过集成学习和添加具有二阶偏导的正则项,提高回归精度和速度,并与LASSO(least absolute shrinkage and selection operator)回归、梯度下降决策树(gradient boosting decision tree, GBDT)、支持向量机(support vector machine, SVM)等机器学习方法进行了对比,以验证本文方法的预测效果;预测过程还对验证集占比、超参数设置、交叉验证(cross validation,CV)等应用要素进行了分析讨论,以期为推进基于机器学习的储层预测技术的发展提供参考。

1 XGBoost基本原理

XGBoost算法是GBDT算法的一种改进,由Chen等于2016年最先提出[6-7],改进后的算法学习效果和训练速度得到了很大的提升。在石油勘探领域,已有多位研究人员在测井资料解释方面开展了很好的应用[8-12]。

XGBoost由多棵决策树组成,通过加法模型将一组弱学习器组合成强学习器。设有数据集(xi,yi),xi为包含m个特征的向量,yi为样本标签,下标i为样本序号,共n个样本,用fk(xi,θk)表示第k棵回归树,θk为对应回归树的参数集,则模型预测值为

(1)

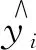
(2)

式中:O为目标函数;L为损失函数,用于评估模型预测值和真实值之间的损失或误差;Ω为正则化项。

不同于常规GDBT方法,XGBoost加入如下正则化项:

(3)

式中:γ、λ为惩罚因子,防止决策树过于庞大;T为叶子数目;ωj为叶子节点j的权重。

考察第s轮训练,式(2)可改写为

(4)

式中,fs为第s轮的预测值。上述目标函数很难在欧氏空间中优化,为此用泰勒展开,近似到二阶导数,得到

(5)

其中:

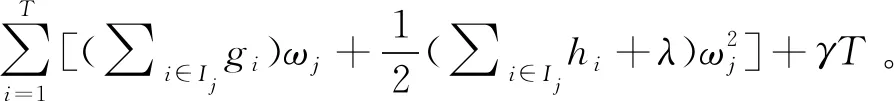
(6)

式中,Ij为叶子节点j的样本集,即落在叶子节点j上的所有样本。式(6)为关于ωj的一元二次函数,由式(6)易解得叶子节点j的最优权重和最优目标函数值:

(7)

(8)

为了避免过拟合,模型训练迭代过程还会加一个缩减系数,以实现小步迭代寻优:

(9)

式中,η为新生成树模型的缩减系数。

图1给出了基于树模型的集成学习原理示意图,通过多棵树加法提高集成度,通过模型迭代求得最优解。另外,XGBoost还支持行采样和列采样,行采样是样本有放回的采样,列采样是部分特征参与训练,目的都是避免过拟合。XGBoost设置了多个模型参数和超参数,通过模型训练获取最佳参数集,进行目标预测。

2 储层厚度预测流程图构建、属性提取与模型测试

2.1 储层厚度预测流程图构建

基于交叉验证的极限梯度提升(CV-XGBoost)砂体厚度预测采取以下主要步骤(图2):一是数据集的准备,主要是地震属性的提取和优化,属性提取尽量选物理意义和地质含义明确的地震属性,属性优化要去除冗余属性,选取井震关系好的地震属性;二是模型训练,建立训练集和验证集,设定超参数,训练集进行网格搜索与交叉验证,通过模型误差评价获取最佳参数集;三是目标预测,将训练好的模型用测试集进行预测,得到预测结果。

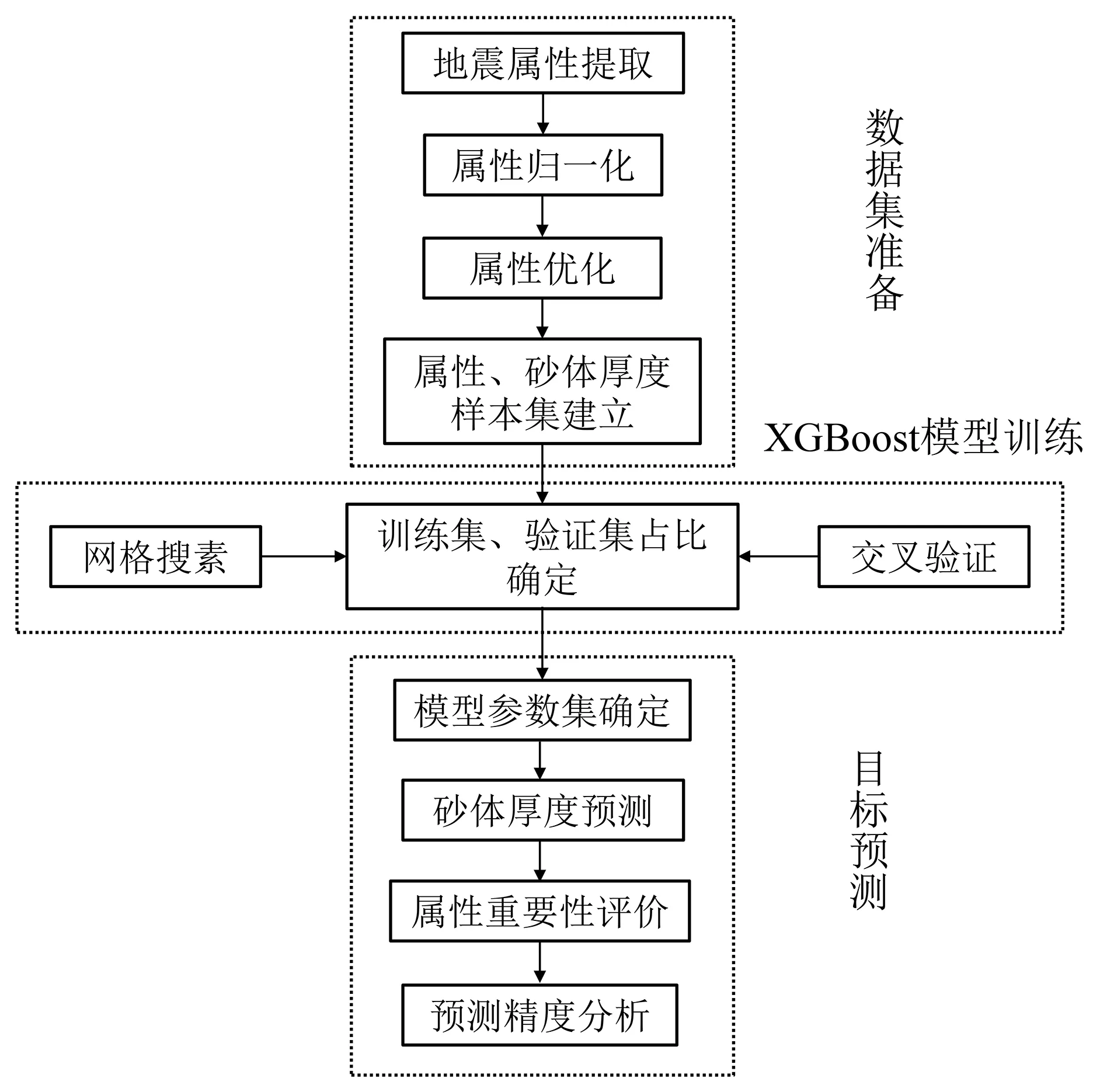
图2 基于CV-XGBoost的砂体厚度预测流程图

2.2 属性提取及共线性评价

以胜利油田通王断裂带通61井区为例,提取物理意义明确、以往储层描述应用效果较好的常用地震属性[13],包括弧长、平均振幅、平均能量、带宽、主频、能量半时、最大振幅、最大幅值、均方根(root mean square, RMS)振幅、总正振幅、过零点数等11个属性,对89口井的井点属性做相关性分析,得到图3所示的Pearson相关系数图。从图3可以看到:RMS振幅、总正振幅、最大振幅、最大幅值相互之间有很强的相关性,另外RMS振幅与平均能量、弧长,最大振幅与平均能量、弧长,总正振幅与平均能量等,也都有很强的相关性。这种相关性,不是单一的一种属性与另一种属性的线性相关,而是具有多重共线性特征的相关。

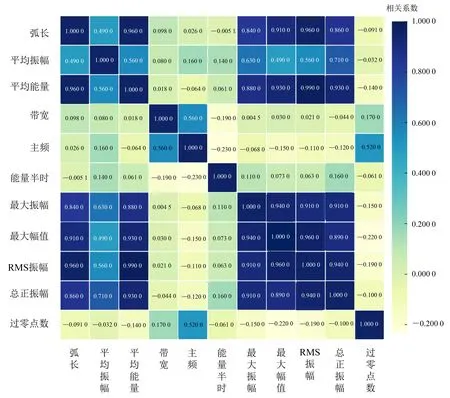
图3 属性Pearson相关系数图

对于多重共线性问题[14],本文还计算了方差膨胀因子(variance inflation factor, VIF),发现RMS振幅多重共线性最严重,VIF达150.34。考察属性的方差比例,在特征值为0.002时,最大振幅与最大幅度的方差比例皆为0.81,大于0.5,由此可知这两个属性也存在多重共线性。综合多属性相关分析、VIF、方差比例结果,最终去除RMS振幅、最大振幅、最大幅度3种冗余属性,用其他8种属性做储层预测。

2.3 XGBoost模型训练及参数集确定

2.3.1 验证集占比的确定

训练集和验证集如何设置,它们对机器学习储层预测有什么样的影响,是一项很有理论研究价值的工作。一般来说,提高训练集的占比会提高模型的预测精度,但相应地会减少验证集占比,而验证集减少会使利用的井数据减少,失去预测价值。为解决这一问题,本文用XGBoost在[5%,95%]间取验证集占比,取值间隔为5%,当预测累积的厚度绝对误差超过100 m时停止模型训练,并通过交叉验证输出最终模型的最佳迭代轮数。经实验,当验证集占比为75%时,触发了停止条件;当验证集占比为80%时,累积的绝对误差已达到了142.12 m。图4给出了不同验证集占比预测结果井点散点图,可以看到:1)当验证集占比较小(25%)时,大多数井预测结果都比较好,只有1口井误差比较大;2)随着验证集占比的提高,验证井增加、训练井减少,实际厚度与预测厚度井点分布逐渐分散,到80%已比较分散。

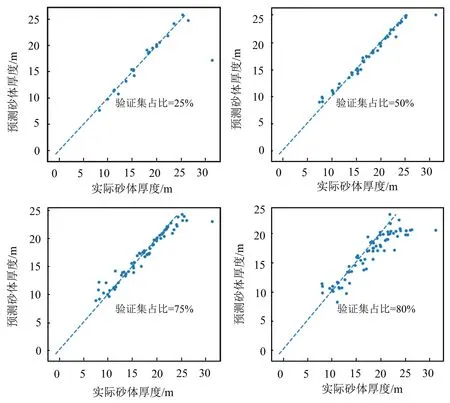
图4 验证集占比与预测精度散点分析图

当验证集占比为25%时,模型最佳参数如表1所示。

表1 最佳模型组合参数

2.3.2 不同方法效果的对比

用LASSO回归[15]、GBDT[16]、SVM[17]与本文XGBoost 4种机器学习方法分别进行预测,并将预测结果与真实的储层厚度进行对比,结果如图5所示。从图5可以看到:LASSO回归方法误差最大,见T61-140、T61-27井;常规的梯度提升方法(GBDT)在T61-617井点处误差较大;SVM方法在T61-33、T61-101井处误差也较大;综合来看,本文XGBoost方法误差最小。表2给出了4种模型预测全部厚度的误差统计,误差评价分别分为平均绝对误差(mean absolute error, MAE)、拟合优度可决系数(R2)、平均相对误差(mean relative error, MRE),整体来看XGBoost误差最小,为最佳方法。

表2 不同机器学习方法预测误差整体评价

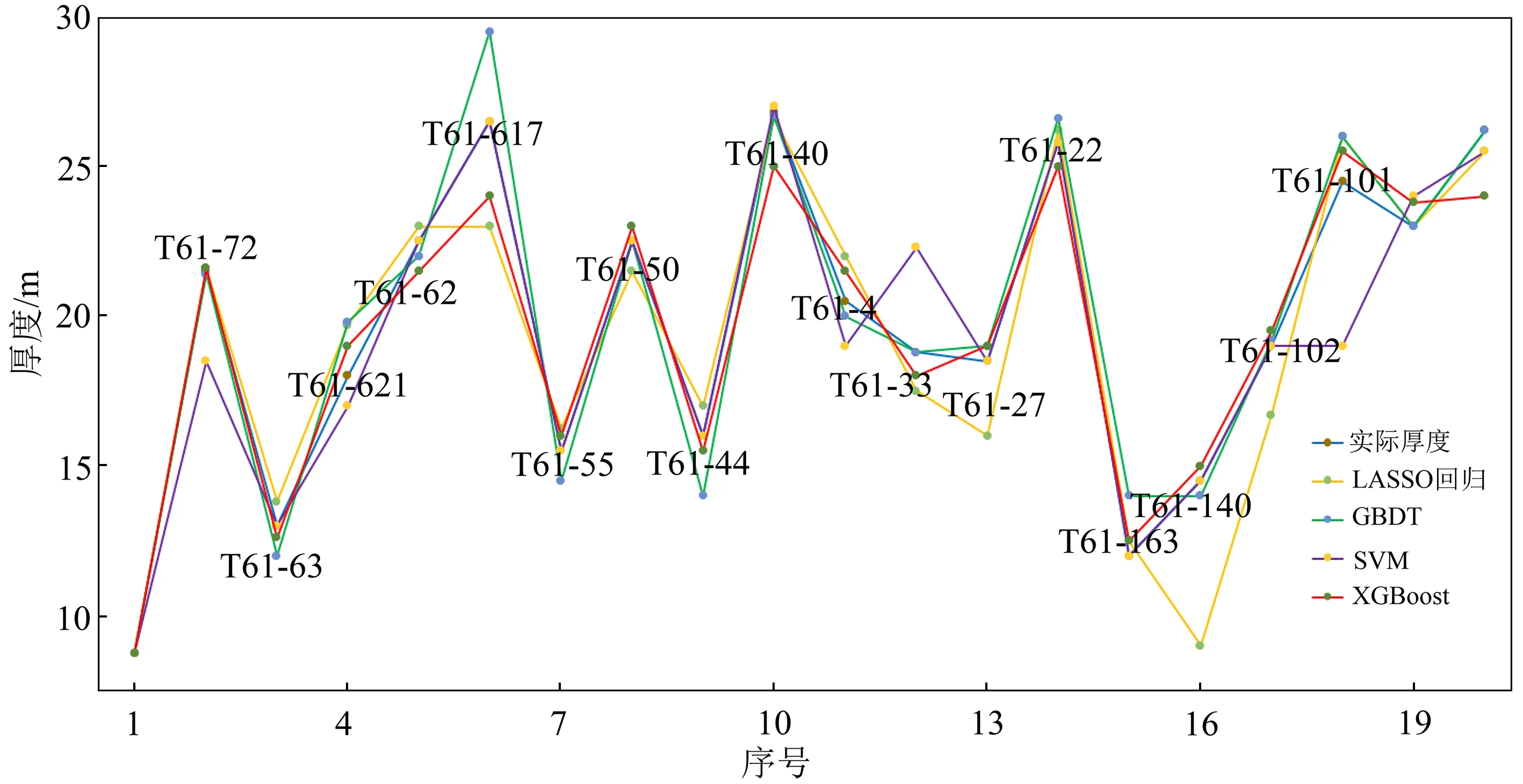
图5 不同机器学习方法预测结果井点误差比较

2.3.3 关于交叉验证模型参数优化的讨论

交叉验证[7],也称为循环估计,是一种统计学上将数据样本切割成较小子集的实用方法,该理论是由Seymour Geisser提出的。其基本思想是在某种意义下将原始数据进行分组,一部分作为训练集,另一部分作为验证集,先用训练集对分类器进行训练,再用验证集来测试训练得到的模型,以此来做为评价分类器的性能指标。交叉验证按类型不同可分为K折交叉验证和留一交叉验证。

本次研究选择K折交叉验证。取75%的井为训练集(66口井),剩下25%的井作为验证集,K取5,做交叉验证测试。图6为交叉验证前后验证集厚度与真实值的对比,可以看到做了交叉验证后预测精度得到明显提高。

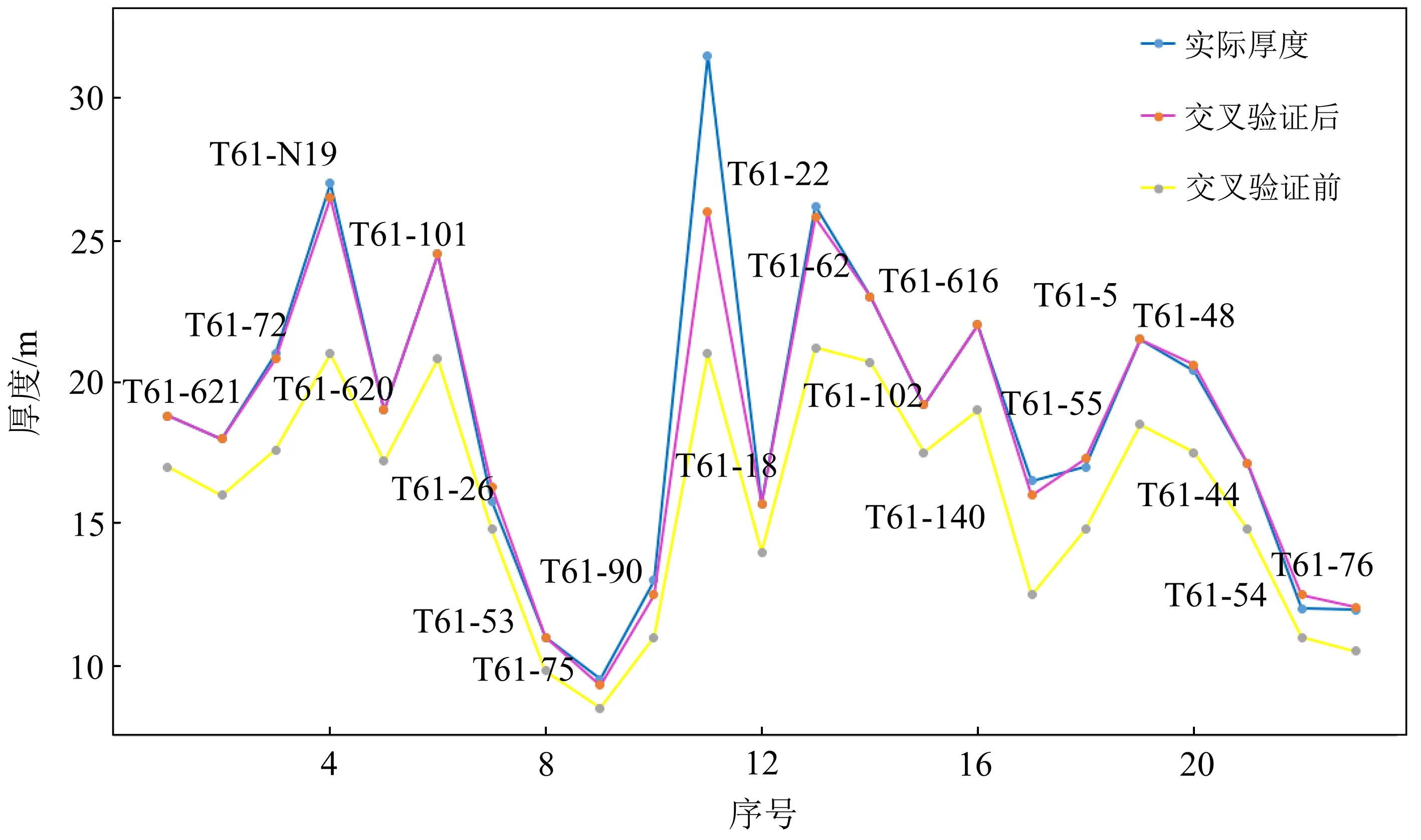
图6 交叉验证前后预测精度比较

3 预测结果分析与评价

根据本文XGBoost方法,得到属性重要性评价结果,如图7所示。从图7可以看出,本研究区平均振幅、平均能量、弧长、主频为厚度预测贡献度较大的属性。

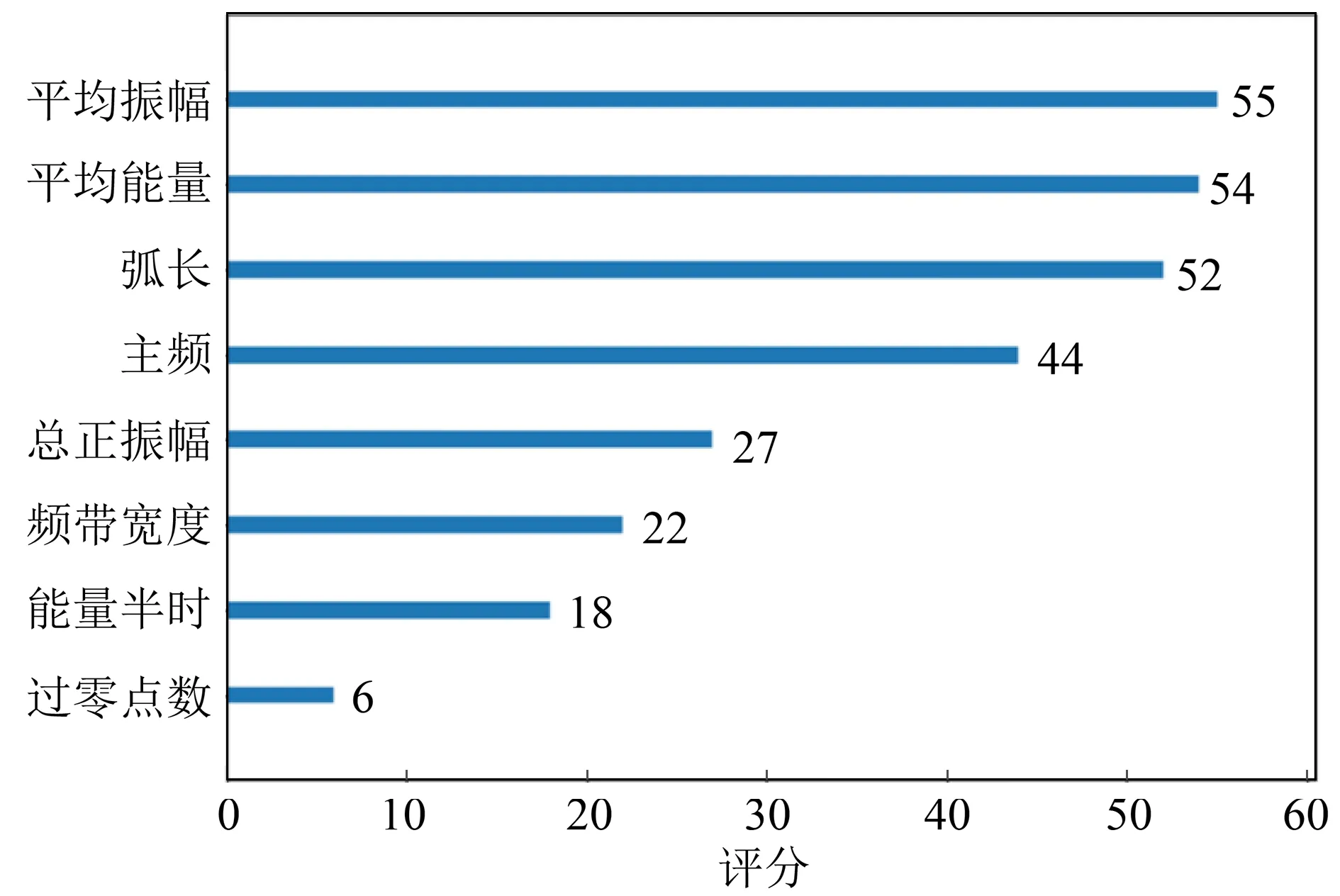
图7 地震属性重要性评分

图8a为根据插值得到的井点厚度图,它没有地震属性的关联信息;图8b、c为本文在不同验证集占比下由XGBoost预测得到的砂体厚度图;图8d为根据前述重要性分析得到的最佳属性。由图8a—c整体来看,砂体有2个厚度中心,这在25%验证集占比情况下特别清晰(图8b),所以要了解研究区砂体的宏观分布,可用较多的训练集、较少的验证集,此认识与图4分析结果一致。仔细观察图8a,右侧存在数据孤立点,这不符合地质认识;从图8b结合图8d地震属性来看,图8b左边的砂体厚度中心范围较大,与属性关联度不高。对比来看,用75%验证集占比预测,虽然如图4分析预测精度会略低于25%验证集,但它参与验证的井多,所蕴含的厚度信息丰富,综合认为是比较合适的预测结果。

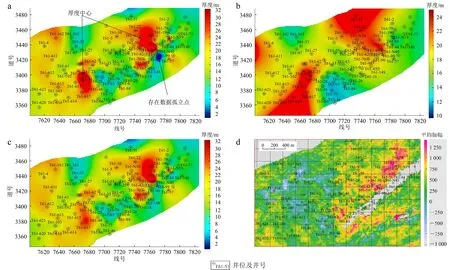
a. 根据插值得到的井点厚度图;b. 本文方法25%验证集占比预测结果;c. 本文方法75%验证集占比预测结果;d. 平均振幅最佳属性。

4 结论

通过CV-XGBoost砂体厚度预测方法研究与实际应用,可以得到以下结论:

1)多重共线性分析技术对去除相关度高的冗余属性、优化模型的数据集十分适用。

2)本文方法具有比LASSO回归、GBDT、SVM方法更高的预测精度,对复杂砂体储层预测具有很好的应用效果,值得在储层预测中推广。