考虑实际接触节理微凸体对剪切强度不同贡献比例的峰值剪胀角模型

班力壬，候宇航，杜伟升，俞 缙，戚承志, ，单仁亮

(1.北京建筑大学 土木与交通工程学院,北京 100044；2.煤炭科学研究总院有限公司 深地科学院,北京 100013；3.华侨大学 岩土工程研究所,福建 厦门 361021；4.中国矿业大学(北京)力学与建筑工程学院,北京 100083)

节理裂隙是控制岩体的变形破坏不可忽视的因素，节理的剪切力学特性比完整岩体的剪切力学特性更应引起工程关注[1-2]。一般而言，影响岩石节理剪切力学特性的因素包括节理的表面形貌特征、法向应力、节理面的接触状态以及充填物质等。对于吻合程度较好、不含充填物质的岩石节理而言，节理表面的形貌粗糙特征和法向应力则是影响其剪切力学行为的主要因素[3-4]。

节理粗糙度作为影响剪切强度的关键因素，其表征方法一直都是岩石力学领域的热点和难点[5]。粗糙度的定量表征方法包括统计参数法和分形法。常见的统计参数有：一阶导数均方根Z2、结构函数SF、迹线长度Rp、均方根RMS、均方值VMS、中心线平均值VCLA等[6]。许多统计参数虽然表征了粗糙度的各向异性特性，然而大部分参数均基于二维轮廓线研究节理表面的起伏度。采用分形理论表征的粗糙度公式很多，其优势在于粗糙度的表征可以独立于测量尺度[7-8]。但有学者认为分形理论获得的粗糙度的公式间通用性较差，分形法没有体现节理粗糙度的三维特性和各向异性特征[9]。这限制了传统统计参数和分形理论在节理剪切理论中的应用和发展。

基于粗糙度的表征方法建立的节理面峰值抗剪强度模型可大致分为3 类：Barton 系模型、Grasselli系模型、其他类型模型。Barton 系模型主要以Barton 提出的JRC-JCS 模型为基础，其研究的重点在于如何定量、精确地确定节理的粗糙度参数JRC[10]。尽管近年来数字化处理技术[11]、小波变换理论[12]等方法在对节理粗糙度的表征和JRC 的获取方面做了新突破，但获取JRC 最常用的方法为：一是与10 条标准轮廓线对比，以主观比较的方式确定JRC；二是通过直剪试验得到的峰值抗剪强度反算JRC。第1 种方法评估粗糙度方式过于主观，第2 种方法则颠倒了工程应用的主次，即研究的目的在于预测峰值剪强度而非通过强度反分析粗糙度。当法向应力趋于0 时，Barton 系模型失去了数学意义。此外，JRC-JCS 模型最突出的问题在于只能截取若干二维轮廓线估算节理面的二维形貌，这种平均化思想过度简化了节理的粗糙度信息，无法充分反映节理形貌的三维特征。

Grasselli 系的节理峰值抗剪强度模型主要基于其提出的三维粗糙度指标体系。GRASSELLI 等[13]通过激光扫描技术获得了节理表面的三维点云，将节理面粗糙不平的起伏近似为三角形的微凸体，运用三角形算法拟合了节理面的有效视倾角分布函数，并提出最大接触面积比A0、最大有效视倾角，粗糙度分布参数C等3 个函数作为表面形貌参数来预测和估算节理面的峰值抗剪强度。YANG 模型[14]、XIA 模型[15]、TATONE 模型[16]均采用了GRASSELLI 提出的3 个表面形貌参数，TIAN 模型[17]将GRASSELLI提出的粗糙度分布参数C修正为C′，上述模型均可视为GRASSELLI 系模型。

除了BARTON 系模型和GRASSELLI 系模型外，学者们还提出了其他类型模型[18-20]。葛云峰[18]提出了一个节理粗糙度的经验模型，其中的粗糙度参数BAP(光亮面积百分比)与BARTON 提出的JRC 的相关性较差。ZHANG 等[19]提出的模型能较好反映节理在正向和反向剪切方向上的各向异性特性，且峰值剪胀角符合节理剪切的边界条件，然其中的2 个粗糙度参数修正的一阶导数均方根Z2与退化参数Cm是2个独立参数，其形式复杂且不易获取，预测精度未得到广泛证实。GHAZVINIAN 模型[20]只能通过直剪试验反算初始剪胀角i0，因而不能预测节理的峰值剪切强度，在实际中应用中还存在不小局限性。而由GRASSELLI 等[21]提出及后续发展的系列模型，由一组关键的形貌参数表征节理表面的粗糙度信息，兼顾对三维形态特征和节理各向异性特性的考虑，且预测的峰值抗剪强度精度较高，是目前较为合适的节理峰值抗剪强度模型。

节理在剪切过程中的损伤退化机理也在逐步被揭示。在建立节理峰值抗剪强度模型时，一般需要考虑节理在剪切方向上的各向异性特性，包括在相反方向上的各向异性(在某一方向和该方向旋转180°对应的方向)。此外，传统的JRC-JCS 模型以JCS(壁面抗压强度，对于未风化新鲜岩石等于岩石的单轴抗压强度)作为材料强度解释直剪试验过程中微凸体的受压破坏尚存在不足。近年来XIA 等[15]、ZHANG 等[19]通过试验证实，节理面表面微凸体多发生拉伸破坏而非受压破坏，因此峰值剪切强度模型中的材料强度项应为节理面壁抗拉强度。GRASSELLI 等[13]指出，在粗糙节理剪切过程中，节理的滑移、啃断等只是一小部分接触区域引起的，接触面上面向剪切方向、最陡的区域与节理的损伤破坏区域及峰值剪切强度有密切联系。BAN 等[22]基于GRASSELLI 形貌分布理论与赫兹接触理论，提出考虑实际接触节理粗糙度的峰值剪胀角模型。这些机理的揭示促进了节理峰值抗剪强度模型的发展。

然而上述研究仅把实际接触微凸体角度的平均值视为节理剪胀角，不同形貌的微元对节理剪切强度的贡献并未考虑。为合理预测节理峰值剪胀角，笔者重点开展GRASSELLI 系列模型的研究，通过考虑实际接触节理微凸体对剪切强度不同贡献比例，推导出了整个节理微凸体等效实际接触节理平均角。将节理微凸体等效实际接触节理平均角等同于节理峰值剪胀角，提出新的节理峰值剪胀角模型。通过现有的研究成果论证了笔者所提峰值剪胀角的合理性，进一步揭示了节理抗剪行为的机理，为相关研究提供参考。

1 GRASSELLI 系列模型简介

GRASSELLI[9]研究发现节理面的真实形貌可用三角形网格微元近似表示，三角形微元可通过节理面测量的数据点生成，而三角形微元的倾角θ、有效视倾角 θ∗、剪切方向与微元倾向的夹角α之间存在一定的几何关系，如图1 所示。

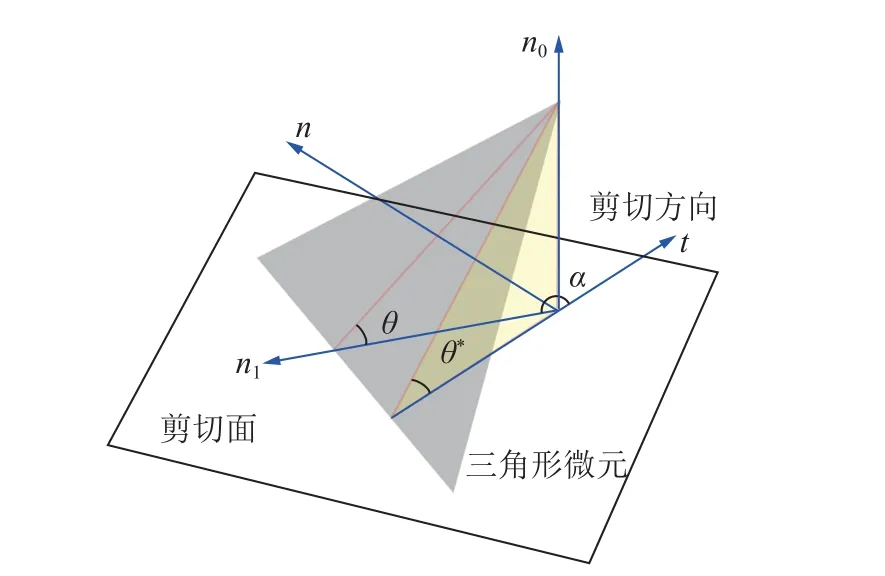
图1 剪切面上三角形微元受剪示意[9]Fig.1 Shear state of the triangle asperity on the shear plane[9]

通过统计数据拟合，发现三角形微元有效视倾角大于 θ∗的微元面积总和与节理面面积比Aθ∗与 θ∗的关系见式(1)[9]：

其中，A0为最大接触面积比，是所有节理微元等效倾角大于0°时的面积总和与节理表面面积总和之比；C为粗糙度分布参数，描述视倾角的分布情况。当C>1 时，式(1)中的函数关系可用图2 表示。

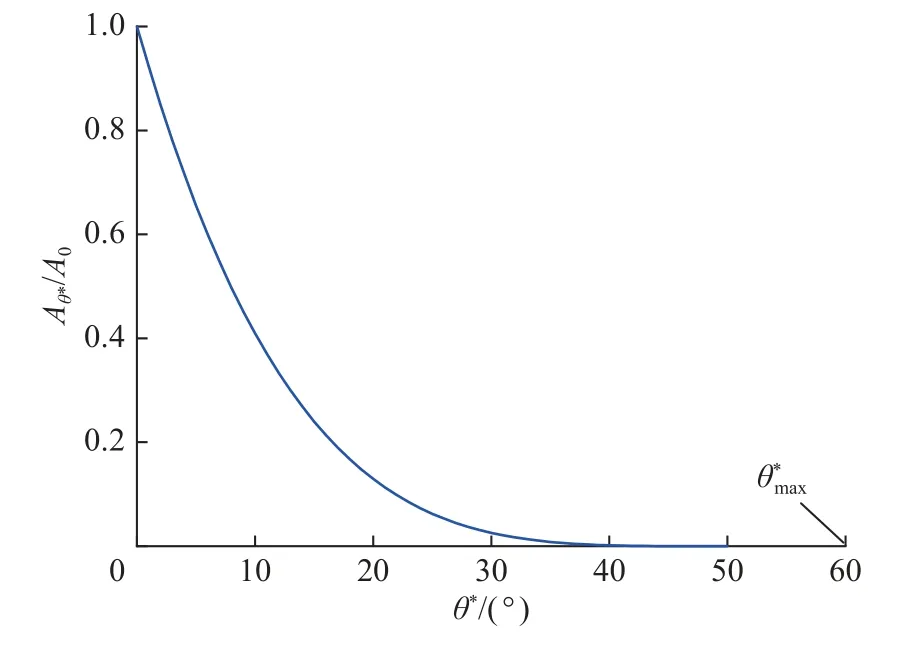
图2 GRASSELLI 视倾角分布函数中 Aθ∗ 与 θ∗的关系Fig.2 Relationship between Aθ∗ and θ∗ in GRASSELLI’s distribution function of apparent dip angle

由图2 可知，随着有效视倾角 θ∗的增大，有效视倾角大于 θ∗的所有微元面积比Aθ∗在减小，最终减小到0。

式中，τp为节理峰值抗剪强度；σn为法向应力；φb为基本摩擦角；φr为残余摩擦角；β为节理面的倾角(一般β=0)；σt为单轴抗拉强度。

TATONE 等[23]计算了图2 曲线下方的闭合面积，对式(1)进行积分，得

式中，l为采样间距，mm。

XIA 等[15]认为GRASSELLI 模型与TATONE 模型不满足摩尔-库伦形式，因此提出式(5)来预测节理峰值抗剪强度：

YANG 等[14]提出节理峰值抗剪强度模型，见式(6)：

式中，σc为单轴抗压强度。

BAN 等[22]基于GRASSELLI 形貌分布理论与赫兹接触理论，提出考虑实际接触节理粗糙度的峰值剪胀角模型，见式(7)：

式中，ip为峰值剪胀角。

BAN 等[22]提出峰值剪胀角即为实际接触节理微元的平均角度，然而不同形貌的微元对节理剪切强度的贡献并未考虑。

节理的峰值抗剪强度符合摩尔-库伦准则[25]，见式(8)：

将式(8)与既有的GRASSELLI 系列模型联立可反推出各模型峰值剪胀角。

2 对剪切强度有贡献的节理微凸体范围与贡献比例

2.1 对剪切强度有贡献的微凸体分布范围

陈曦等[25]研究发现节理在剪切时受到的阻力只是一小部分较陡的微凸体产生的，式(1)中C的增大会导致较陡的视倾角面积比含量降低，节理粗糙度也会降低。当C增大，节理中较陡视倾角的减少才是引起节理粗糙度降低的根本原因，而非较平缓视倾角的增大。因此，对节理粗糙度的研究应当重点关注较陡的视倾角而非较平缓的视倾角。

对于岩石节理在法向应力下的剪切问题，实际接触面积Ac可以近似认为是作用在节理面上法向荷载N除以岩石的单轴抗压强度σc[22]，见式(9)：

式中，A为节理面名义面积。

式中，Aθ∗cr/A0为面向剪切方向接触面积与面向剪切方向所有节理微凸体面积的比，约等于Ac/A[22]。

基于以上假设，结合式(9)、(10)，得到所有接触微凸体中的最小倾角，有

由式(11)可确定实际接触节理的最小角度。剪切过程中实际接触的微凸体才对剪切强度有贡献，那么对剪切强度有贡献的部分为视倾角在的微凸体。对于视倾角在(0，)的微凸体在研究节理剪切强度时应该予以剔除。

2.2 实际接触节理中各部分微凸体对强度的贡献比例的确定

KWON 等[26]研究了长方体微凸体的破坏模式，如图3 所示，长方体微凸体高度为h，长度为b，几何参数m=h/b，法向荷载为N，切向荷载为T。当mmc时，破坏模式为剪断破坏。

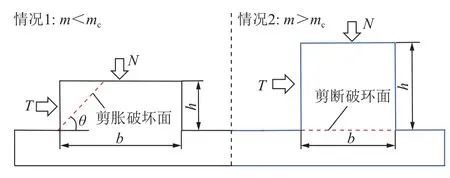
图3 长方体微凸体破坏模式Fig.3 Failure modes of rectangular-shaped asperity

临界几何参量mc如式(12)[26]所示：

式中，c、φf分别为完整岩石的黏聚力与峰值摩擦角。

单个长方体微凸体的剪切强度[26]如式(13)所示。由式(13)可知，对于确定材料的岩石节理微凸体，当m小于临界几何参数mc时，剪切强度随着m增加线性增加，达到临界几何参数后保持不变。

上述是将节理微凸体等效为长方形微凸体进行分析，对于微小的单元等效为长方形单元与三角形单元是相似的。因此将节理等效为三角形微凸体也应具有以上类似性质。假设微凸体的临界形状参数mc对应的倾角为临界角度，则对于确定材料的岩石节理三角形微凸体，当等效倾角 θ∗小于临界角度时，剪切强度随着 θ∗增加线性增加，即剪切强度正比于 θ∗；等效倾角 θ∗大于临界角度时，剪切强度不变，正比于。

综合2.1 节，在岩石节理面上抵抗剪切的阻力是由面向剪切方向上所接触微凸体产生的，所接触微凸体最小角度为。对于 θ∗在的微凸体，其破坏模式为剪胀破坏，对剪切强度的贡献正比于 θ∗；对于 θ∗在的微凸体，其破坏模式为剪断破坏，对剪切强度的贡献正比于。

3 考虑实际接触节理微凸体对剪切强度不同贡献比例的峰值剪胀角模型

陈曦等[25]研究表明GRASSELLI 分布函数中的C与能够描述有效视倾角的分布情况和“含量”情况，类似于土壤颗粒粒度分析过程。将GRASSELLI分布函数进行变式，将A0移到等式左侧得

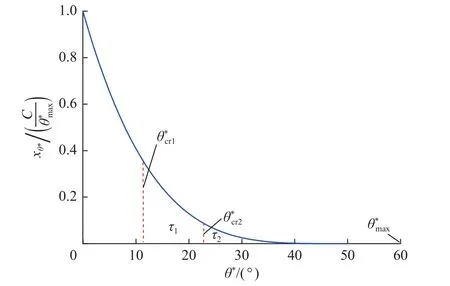
图4 与θ∗的关系Fig.4 Relationship between and θ∗

故所有剪胀破坏微凸体的剪切强度τ1，可由式(16)求得

对于 θ∗在间的微凸体，其破坏模式为剪断破坏，对剪切强度的贡献正比于。则所有剪断破坏的三角形微凸体强度正比于与所有等效倾角为θ∗的三角形单元含量乘积之和。所有剪断破坏微凸体的剪切强度τ2，可由式(17)求得

则所有面向剪切方向微凸体的抗剪强度τ3，如式(18)所示：

BAN 等[22]发现实际接触节理微凸体的平均角度为节理峰值剪胀角。然而上述研究仅从实际接触节理形貌分布角度来提出峰值剪胀角，节理峰值剪胀角是为预测节理剪切强度服务的，峰值剪胀角应该从物理意义上与节理剪切强度联系起来。本文考虑实际接触节理微凸对剪切强度的不同贡献，提出了一个可与剪切强度相联系的等效实际接触节理平均角；实际接触节理平均倾角即为剪胀角，所提等效实际接触节理平均角即为新的峰值剪胀角模型，如式(19)所示。

4 模型验证

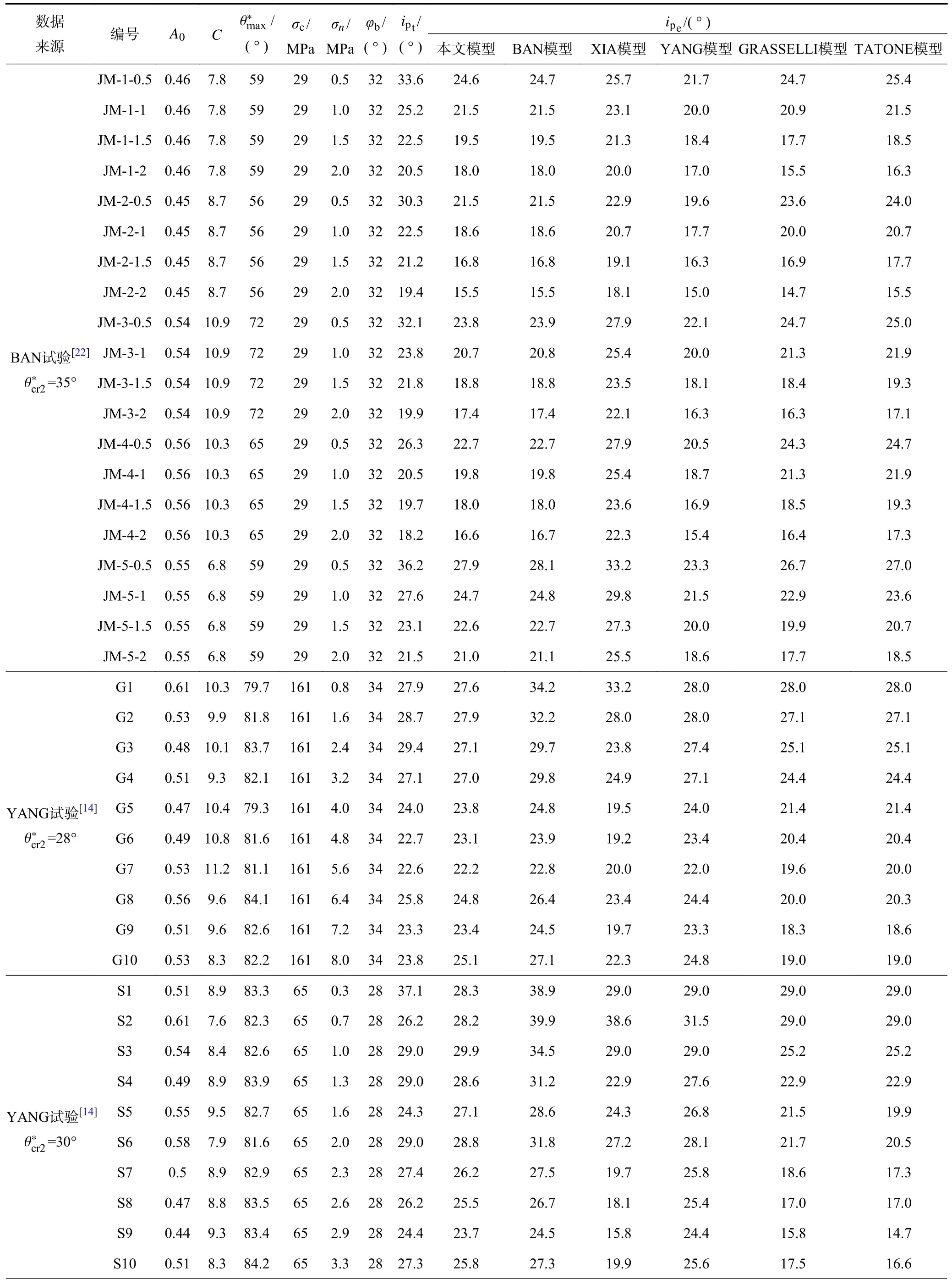
表1 各学者试验数据以及模型计算结果Table 1 Test data and calculation results of different scholars

为对各个模型进行评价，选取相对误差平均值来定量描述各模型的精度。

相对误差平均值δ的计算，如式(20)所示：

经计算本文提出的峰值剪胀角新模型估算的相对平均误差为14%，BAN 模型平均误差为14%，GRASSELLI 模型估算的平均误差为17%，XIA 模型估算的相对平均误差为13%，YANG 模型估算的相对平均误差为21%，TATONE 模型估算的相对平均误差为14%。

鉴于节理试样的岩性对剪切行为的影响，下面用不同学者们为不同岩性的节理试样实施剪切试验的结果来验证本模型。

根据YANG 等[14]发表的10 组花岗岩试验结果，采用最小二乘法拟合得到=28°。表1 展示了YANG 的试验结果与上述6 种模型的预测结果对比。经计算本文提出的峰值剪胀角新模型估算的相对平均误差为3%，BAN 模型平均误差为8%，GRASSELLI模型估算的平均误差为13%，XIA 模型估算的相对平均误差为13%，YANG 模型估算的相对平均误差为25%，TATONE 模型估算的相对平均误差为12%。

根据YANG 等[14]发表的10 组砂岩试验结果，采用最小二乘法拟合得到=30°。表1 展示了YANG的试验结果与上述6 种模型的预测结果对比。经计算本文提出的峰值剪胀角新模型估算的相对平均误差为6%，BAN 模型平均误差为11%，GRASSELLI 模型估算的平均误差为24%，XIA 模型估算的相对平均误差为22%，YANG 模型估算的相对平均误差为8%，TATONE 模型估算的相对平均误差为26%。

根据XIA 等[15]发表的10 组砂岩试验结果，采用最小二乘法拟合得到=40°。表1 展示了XIA 的试验结果与上述6 种模型的预测结果对比。经计算本文提出的峰值剪胀角新模型估算的相对平均误差为14%，BAN 模型平均误差为14%，GRASSELLI 模型估算的平均误差为19%，XIA 模型估算的相对平均误差为13%，YANG 模型估算的相对平均误差为16%，TATONE 模型估算的相对平均误差为19%。根据TATONE 等[23]发表的6 组砂岩试验结果，采用最小二乘法拟合得到=40°。表1 展示了TATONE 的试验结果与上述6 种模型的预测结果对比。经计算本文提出的峰值剪胀角新模型估算的相对平均误差为4%，BAN 模型平均误差为4%，GRASSELLI 模型估算的平均误差为8%，XIA 模型估算的相对平均误差为11%，YANG 模型估算的相对平均误差为22%，TATONE 模型估算的相对平均误差为6%。

根据GRASSELLI[9]发表的7 组石灰岩节理试验结果，采用最小二乘法拟合得到=28°。表1 展示了GRASSELLI 试验的试验结果与上述6 种模型的预测结果对比。经计算本文提出的峰值剪胀角新模型估算的相对平均误差为4%，BAN 模型平均误差为15%，GRASSELLI 模型估算的平均误差为5%，XIA模型估算的相对平均误差为9%，YANG 模型估算的相对平均误差为6%，TATONE 模型估算的相对平均误差为5%。

根据GRASSELLI[9]发表的7 组花岗岩节理试验结果，采用最小二乘法拟合得到=35°。表1 展示了GRASSELLI 的试验结果与上述6 种模型的预测结果对比。经计算本文提出的峰值剪胀角新模型估算的相对平均误差为5%，BAN 模型平均误差为23%，GRASSELLI 模型估算的平均误差为8%，XIA 模型估算的相对平均误差为5%，YANG 模型估算的相对平均误差为8%，TATONE 模型估算的相对平均误差为6%。

根据Grasselli[9]发表的11 组大理岩节理试验结果，采用最小二乘法拟合得到=28°。表1 展示了GRASSELLI 的试验结果与上述6 种模型的预测结果对比。经计算本文提出的峰值剪胀角新模型估算的相对平均误差为12%，BAN 模型平均误差为14%，GRASSELLI 模型估算的平均误差为16%，XIA 模型估算的相对平均误差为11%，YANG 模型估算的相对平均误差为11%，TATONE 模型估算的相对平均误差为16%。

根据GRASSELLI[9]发表的3 组节理试验结果，采用最小二乘法拟合得到=28°。表1 展示了Grasselli的试验结果与上述6 种模型的预测结果对比。经计算本文提出的峰值剪胀角新模型估算的相对平均误差为21%，BAN 模型平均误差为23%，GRASSELLI模型估算的平均误差为66%，XIA 模型估算的相对平均误差为40%，YANG 模型估算的相对平均误差为22%，TATONE 模型估算的相对平均误差为9%。

将BAN 等[22]、GRASSELLI[9]、XIA 等[15]、YANG等[14]、TATONE 等[23]的89 组试验数据汇总分析平均误差，如图5 所示(图5 与图6 中斜直线为数据拟合直线，直线越接近y=x，表明模型精度越高)。本文提出的峰值剪胀角新模型估算的相对平均误差为10%，BAN 模型估计的误差为13%，GRASSELLI 模型估算的平均误差为17%，XIA 模型估算的相对平均误差为13%，YANG 模型估算的相对平均误差为13%，TATONE 模型估算的相对平均误差为14%。由此可知在数据比较多时本文模型精度属于最好的。

图5 所得节理峰值剪胀角试验结果与本模型计算结果对比Fig.5 Comparison of test results and calculation results of the peak shear strength model

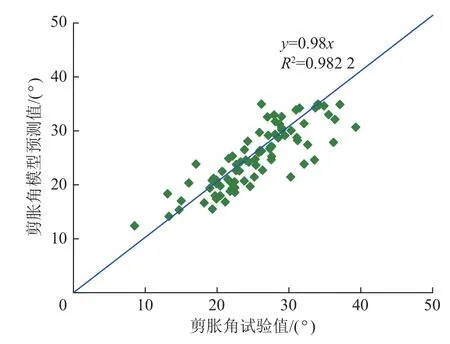
图6 =32°时所得节理峰值剪胀角试验结果与本模型计算结果对比Fig.6 Comparison of test results and calculation results of the peak shear strength model with =32°

5 讨论

根据第4 节验证结果，对于部分试验数据，BAN模型与新模型预测精度相差不大；而对于另外的试验结果，新模型预测结果明显优于BAN 模型。为解释上述情况，笔者探讨不同C、对的影响。当=70°，σn=1 MPa，A0=0.5，σc=27.5 MPa，取C=3、5、7 时，分析随着变化，的变化，如图7 所示。

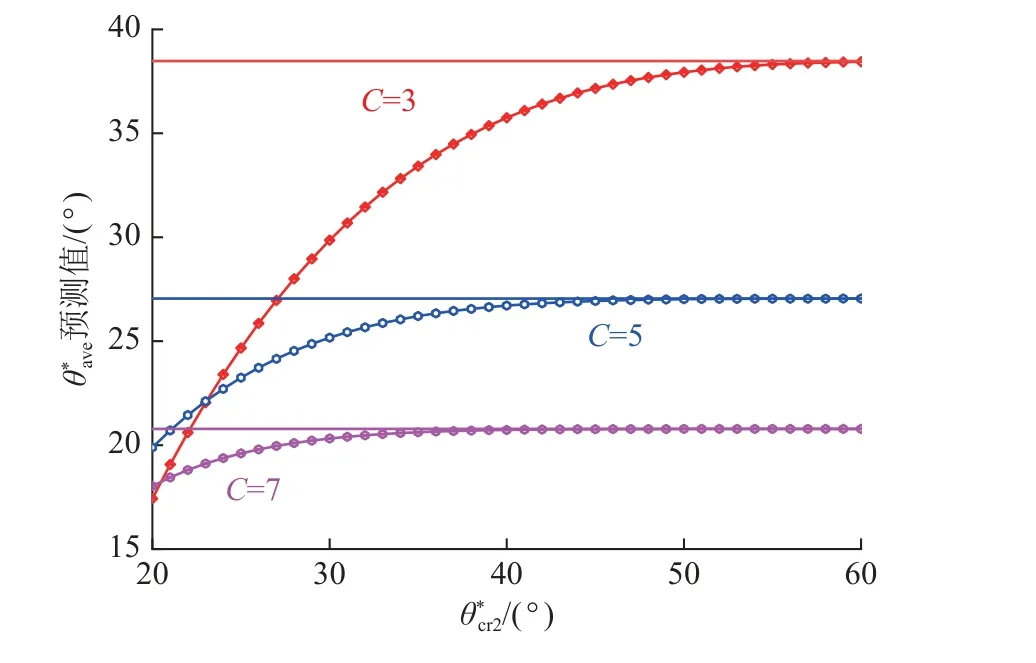
图7 与预测值关系Fig.7 Relationship between and

图7 中实线为BAN 模型预测值，点划线为新模型预测值。由图7 可知，当C一定时，随着增大，以类似抛物线的形式逐渐变大，并且趋于BAN 模型预测值；随着C的增大，BAN 模型与新模型的预测值都在降低。其中BAN 模型由39°减小为27°、21°。当=32°时，新模型由32°减小为26°、20°。这是因为C的增大会导致较陡的视倾角的面积比含量降低，节理粗糙度也会降低，进而节理峰值剪胀角减小。同时由图7 可知，随着C的增大，2 个模型的差值也会降低。当=32°的情况下，C=3 时，两模型的差值为8°；C=5 时，两模型的差值为4°；而C=7 时，两模型的差值为1°。这表明，在C较大时，两模型的预测结果较为接近；而C较小时，新模型的预测精度要高于BAN 模型。因此是否考虑对于不同形貌的节理有着不同的影响。

由图7 可知，当C较小时，对模型的预测结果影响较大。通过89 组实验数据的拟合结果，笔者确定了约为32°。根据共89 组试验数据汇总分析平均误差仅为11%，与其他模型比较所得结果精度最高。上述仅从试验结果拟合确定了，并未从物理机理上去解释。因此有必要对取值在理论上的解释进行一些阐述。

对于长方体微凸体，由式(12)可知临界几何参量与岩石材料性质、法向应力有关。在低法向应力下[27]，式(12)可进行简化，即

由式(21)可知，mc仅与峰值内摩擦角关系较大。式(12)是节理形貌由连续长方体微凸体划分所得的理论计算结果。如采用三角形划分节理形貌，将微凸体由长方体转变为三角形微凸体，则可将微凸体最高点等效为三角形微凸体顶点，划分间距为三角形的最底部长度。图8 表示微凸体为剪断破坏模式时长方体与三角形微凸体的划分情况，绿色实体部分为划分的三角形微凸体。

图8 采用长方形与三角形微凸体划分网格时的示意Fig.8 Schematic diagram of grid generation with rectangular and triangular asperities

对于长方形微凸体，其临界几何参数为mc，破坏面沿微凸体的根部。由图8 可知，将节理面等效为连续三角形微凸体时，三角形临界角度如式(22)所示。

常见岩石内摩擦角通常为21°～40°，可取30°[28]。代入式(22)可得为25°～35°，通常为30°左右。因此，由89 组试验结果拟合获得的=32°有一定合理性。

新模型的应用需要获取一些节理微观参数，对于一些工程中这些参数的获取较为困难。以上针对上述情形对模型进行了简化，取试验拟合的=32°来统一确定新的峰值剪胀角模型，上述对模型的简化的研究可以拓展新模型的适用范围。

6 结论

(1)在岩石节理上抵抗剪切的阻力是由面向剪切方向的所接触微凸体产生的。对于 θ∗在(，)的微凸体，其破坏模式为剪胀破坏，对剪切强度的贡献正比于 θ∗。而 θ∗在的微凸体的破坏模式为剪断破坏，对剪切强度的贡献正比于。

(2)根据实际接触节理微凸对剪切强度不同贡献比例，推导出了等效实际接触节理平均角。将等效实际接触节理平均角等同于节理峰值剪胀角，提出新的节理峰值剪胀角模型。该指标物理意义明确，TATONE与BAN 所提粗糙度指标仅仅是本文所提新指标的一种特殊情况。

(3)用以往学者的89 组试验数据对分析了模型的预测能力。本文提出的峰值剪胀角新模型估算的相对平均误差为10%，BAN 模型估计的误差为13%，GRASSELLI 模型估算的平均误差为17%，XIA 模型估算的相对平均误差为13%，YANG 模型估算的相对平均误差为13%，TATONE 模型估算的相对平均误差为14%。在数据较多时，本文模型精度较好。