采场等效孔模型及主应力旋转规律

刘洪涛，陈子晗，郭晓菲，韩子俊，刘勤裕，韩 洲，张红凯

(中国矿业大学(北京)能源与矿业学院,北京 100083)

矿井巷道的非对称破坏是巷道研究中重点考虑的问题。相关研究表明，采场开挖导致的煤岩体加卸载运动及覆岩运移会导致支撑煤体内应力矢量发生显著变化[1-3]，这种应力值与应力方向的双重变化是巷道出现非对称破坏的主要原因[4-8]。马念杰等[10]、赵志强等[9，11-12]推导了非等压条件下圆形巷道周围的塑性区边界方程，发现了区域主应力的比值变化会使巷道围岩出现蝶形塑性区，一定程度上利用蝶形模型解释了巷道非对称破坏现象。李季等[13]依据蝶形破坏理论对碟叶的方向性机制展开研究，发现主应力的方向变化会引起围岩塑性区碟叶的偏转，造成巷道围岩的破坏位置产生变化。因此，对采场侧方的应力场旋转现象展开研究，探究采场侧方支承煤体中主应力的旋转规律与机理，利用一个合理的模型对采场侧方煤体中的主应力旋转现象进行描述，对采场侧方巷道的破坏特征分析有着重要的意义。

一直以来，众多学者对开采而引起的应力场方向变化及其影响进行了大量的探讨和研究。王兆会等[14]、王家臣等[15]对深井超长工作面采动应力旋转展开研究，发现了采动应力旋转可以控制顶板并指导工作面推进方向的优化。贾后省等[16]分析了采动巷道应力场特征，并发现了采场侧不同位置围岩主应力大小、比值和方向具有明显差异。崔溦等[17]研究了隧洞开挖过程中应力主轴旋转下岩体的裂隙扩展模式，发现应力方向的旋转会造成围岩中的初始裂隙扩展深度和方向发生变化，影响围岩破坏模式。赵洪宝等[18]对三向应力下的偏应力场进行研究，并验证了主应力方向旋转会引起偏应力旋转，提出了巷道非对称支护技术。陈上元等[19]采用相似模拟和现场试验相结合，对巷道非对称大变形进行研究，发现了采动应力造成巷道围岩应力场的大小和方向改变，是巷道产生非对称变形的主要因素。冯国瑞等[20]采用理论分析与数值模拟对非对称变形展开研究，发现采空区和遗留煤柱下方支承应力改变了巷道最大主应力的大小和方向，造成巷道发生非对称变形。

上述研究均发现了主应力方向变化在巷道破坏与岩层控制中的重要作用。而目前的研究仅是对主应力方向变化所产生的影响进行探讨，并未对主应力方向旋转现象产生的原因与规律进行系统性研究。因此，通过等效[21]的概念，建立理想化的采场等效孔模型，将理论计算与数值模拟相结合，重点对采场侧方主应力旋转的形成机制与规律展开研究。

1 巷道塑性区形成及主应力旋转影响

1.1 巷道蝶形塑性区的形成

实际工程中，巷道周围的应力环境通常是十分复杂的。在研究巷道问题时，一般将巷道简化为弹塑性力学中轴对称圆孔的平面应变问题，即不考虑巷道在轴向方向上的应变，力学模型如图1 所示。其中P1为模型边界的最大主应力，P3为模型边界的最小主应力，R为巷道半径，r、θ为模型中任意一点的极坐标，侧压系数λ为P1和P3的比值(式(1))。

图1 非均匀应力场圆形巷道力学模型Fig.1 Mechanical model of circular roadway in inhomogeneous stress field

对巷道而言，其周围一般为非均匀应力场，此应力场会受到巷道埋深、巷道周围地质构造等因素的影响，最大主应力与最小主应力存在差异，即侧压系数λ≠1。在工作面、硐室等开挖之后，巷道周围应力场的非均匀程度将更加明显。这种应力场的非均匀化会引起巷道周边围岩塑性区的变化，对巷道稳定性造成影响。

对非均匀应力场下圆形巷道塑性区的问题，马念杰等[10]、赵志强等[9，11-12]推导了非等压条件下的圆形巷道的塑性区边界隐性方程，提出了蝶形塑性区的概念，对其形成机制及工程意义进行了详细阐述，蝶形塑性区形态如图1 中红色实线部分所示。非均匀应力场下的巷道塑性区将受到侧压系数、埋深等因素的影响，塑性区会随着侧压系数的增大而由圆形变为椭圆形，最终变为蝶形，且蝶形塑性区的扩展速度会随着侧压系数的增加而上升。蝶形塑性区的出现会致使巷道周边围岩出现不规则破坏，巷道围岩稳定性降低，顶板垮落和支护失效的可能性增加。

1.2 主应力旋转现象及其实际意义

现有研究表明，伴随着采场开挖，其侧方巷道会出现不规则的破坏，巷道围岩会出现较深的破坏区，即巷道塑性区受采场扰动而转变为蝶形。但塑性区碟叶出现的位置并不会如图1 所示，而是会发生一定角度的偏转，即围岩最深破坏位置转移到巷道帮部或者顶板，从而造成巷道帮部或者顶板围岩失稳。这种巷道围岩塑性区的偏转取决于巷道周边的主应力状态变化，即由采场开挖而造成的主应力方向的偏转。当巷道周边的主应力方向发生偏转时，巷道围压塑性区会出现偏转，这种偏转会导致塑性区的碟叶位置发生变化。李季等[13]将主应力方向偏转角度α代入马念杰、赵志强等推导的非等压条件下的圆形巷道围岩塑性区边界隐性方程中，通过因式分解，得到了围岩塑性区方向主应力偏转角度α与极坐标位置角度θ的余弦四次隐性方程，其计算公式如式(2)所示。

式中，r为塑性区边界上一点距巷道中心的距离；C为巷道周围岩体的黏聚力；φ为内摩擦角；θ为塑性区边界上一点的极坐标角度；α为主应力偏转角度(定义为最大主应力P1与水平方向的夹角，顺时针为正)。

由式(2)可以得知，当主应力角度α发生变化时，巷道围岩的塑性区也会相应的发生转动。在塑性区是圆形或者椭圆形时主应力的转动影响较小，但是当围岩塑性区进入蝶形风险状态后，主应力的转动就尤为重要，转动的角度将预示着巷道周围可能的破坏位置与区域。利用式(2)计算的塑性区旋转示意如图2所示。

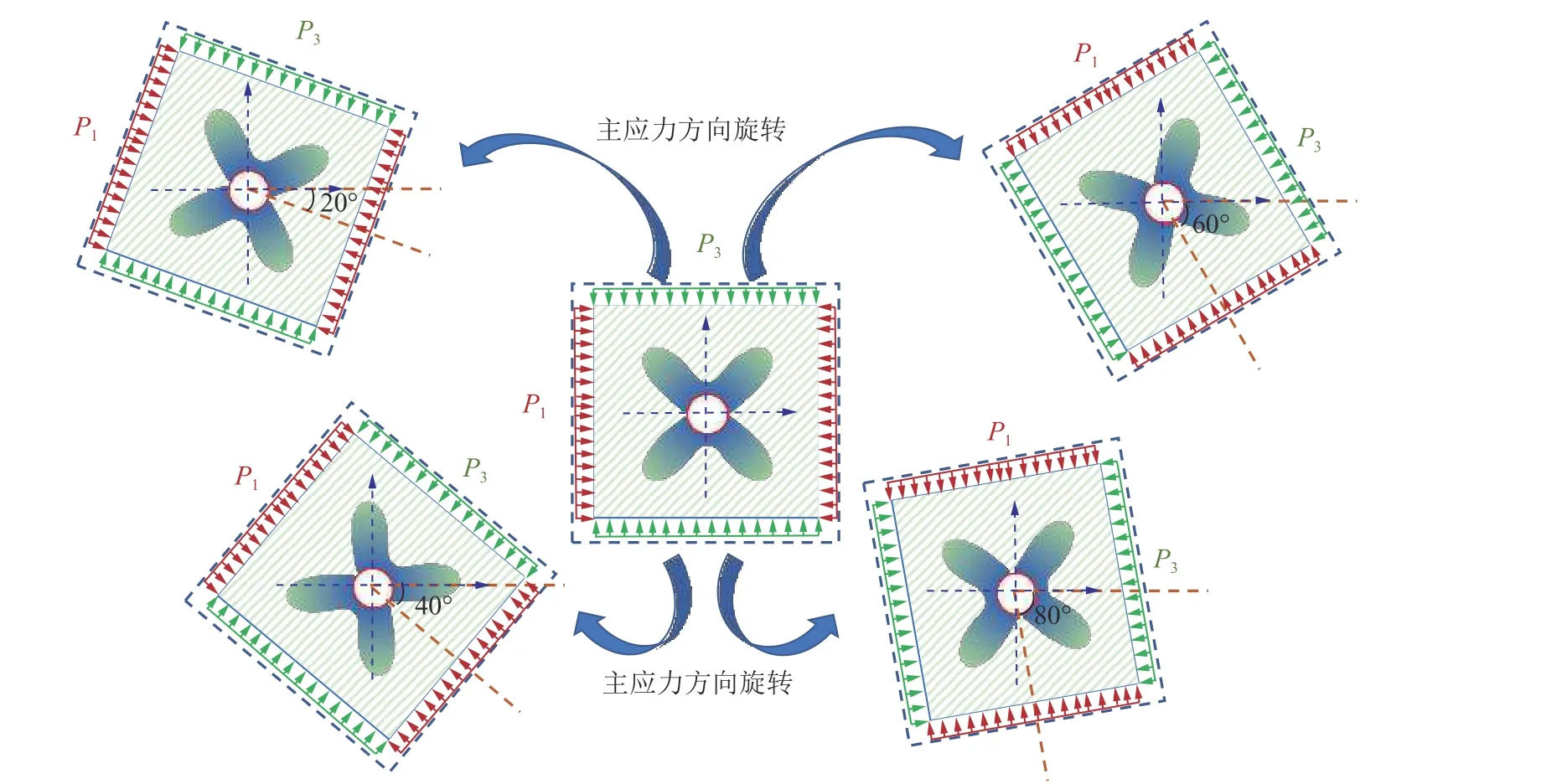
图2 改变α 时塑性区旋转示意Fig.2 Schematic diagram of plastic zone rotation when α is changed

由图2 可知，当巷道周围侧压系数较大，其塑性区处于蝶形的危险状态时，若主应力角度旋转较小，则围岩破坏最深处位于巷道的2 个帮角。随着主应力旋转角度的增大，围岩破坏最深处会偏转到巷道顶板和帮部，造成大范围的顶板冒落与帮部支护失效。因此，研究采场侧方主应力方向的旋转规律具有一定的工程意义。通过对采场侧方的主应力方向的形成机理进行研究，提供一种较为可靠的简化模型来计算采场周围的主应力旋转角度，对巷道塑性区的偏转角度做出预测，对巷道围岩支护具有一定的指导意义。

2 采场等效孔模型及理论旋转规律

2.1 采场等效孔模型与主应力方向的确定

以往学者在研究采场与巷道问题时，都将其简化为一个等压孔，在等压孔的周边取一块单元体进行静力平衡求解，并代入极限平衡的条件，求出工作面前方与巷道侧方的切向应力与轴向应力分布，并将切向应力的增高部分定义为支承压力。对工作面而言，采空区并未压实，采空区内尚未形成与初始应力相当的有效的支承应力，故将工作面视为一个孔是一种理想化的简化。

实际上，不仅是对于工作面前方可以如此简化，对工作面侧方以及采空区侧方研究时，由于工作面内和采空区内均没有与初始应力相当的有效的支承应力，故对工作面和采空区侧方煤体中的主应力旋转角度研究时，也可将其视为理想化的孔。但工作面与巷道不能被视为等压孔，因为实际的工程中，工作面与巷道周围初始地应力场通常是非等压的。

受到采场开采的扰动，采场侧方煤体的支承应力集中系数会升高到初始地应力的1～3 倍，其最大主应力方向由初始状态变为竖直方向。随着往煤体深部深入，最大主应力的方向则会由此区域的原始地应力决定。可以预测，埋深较浅时，水平方向的地应力大于垂直方向的地应力，则随着向煤体深部深入，最大主应力的方向将逐渐由竖直转为水平。埋深较深时，地质构造作用减弱，垂直方向的地应力将大于水平方向的地应力，故最大主应力方向应一直处于垂直状态，不会发生大范围的偏转。

实际工程中，采场的开挖会导致上覆岩层的运移，采场周围结构较为复杂，想要构筑一个准确直观的模型非常困难，故需对工作面和采空区进行理想化简化，即忽略工作面和采空区的上部结构。由于工作面内和采空区内没有与初始应力相当的有效应力，工作面与采空区给予了侧方未开挖煤体一个卸压的方向，故可以将工作面与采空区理想化地等效为非等压孔，其周边的初始地应力决定了此非等压孔的侧压系数。研究此非等压孔一侧的主应力旋转特征，即可近似于研究采场侧方煤体的主应力旋转特征。此简化模型为理想化模型有3 个前提假设：①忽略工作面上覆岩层结构，视其为均质连续弹性体。②巷道周围主应力方向由采场引起的主应力方向决定，不考虑巷道自身引起的主应力方向变化。③不考虑推进方向上的变化，将采场与侧方煤体的整体研究视为平面应变问题。

为了便于进行理论计算，将采场侧方塑性区边界线之内简化为非等压孔，非等压孔的形状取为圆形，简化图像如图3 所示。

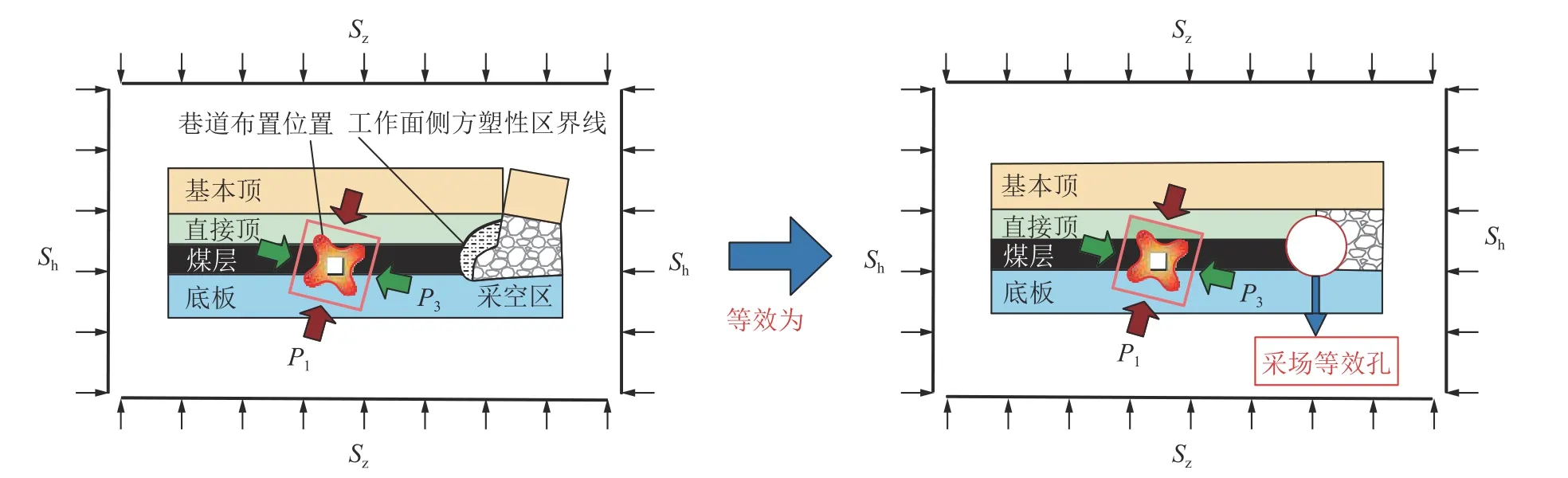
图3 采场等效孔模型示意Fig.3 Schematic diagram of stope equivalent hole model

采场周围的初始地应力侧压系数为η，垂直方向的载荷记为Sz，水平方向载荷记为Sh，则η=Sh/Sz。孔周边的径向应力、切向应力与剪切应力分别为σr、σθ、τrθ采场等效孔的半径实际上反映了推进方向上不同位置的采场对侧方煤体的扰动程度，半径越大则扰动程度越高，半径越小则扰动程度越低，其值将由采高、开采方式、顶板处理方式、工作面支护能力等因素决定。此理想化的等效孔实际上是不存在的，笔者仅利用其对采场侧方的主应力旋转规律展开研究，提供一种可以进行采场侧方主应力旋转角度计算的思路。

对非等压圆孔，可利用弹性力学中非等压圆形孔周边的应力表达式，如式(3)所示。

由非等压圆形孔周边的应力表达式可知，当θ=0°时，即位于圆孔中轴线位置上，剪应力为0，圆孔周边的主应力方向旋转是一个突变的过程，最大主应力方向会由切向应力方向突变成径向应力方向。因此，用圆孔中轴线上的单元体的应力状态描述采场侧方的主应力旋转角度显然是不合理的。笔者将等效孔上边界的由孔边向外部延伸的一系列单元体定义为靶向单元体，其与孔心的水平距离为x+R，将其与孔心连线，取连线上距离孔心同样为x+R的单元体为特征单元体，取特征单元体的方式如图4 所示，则θ可表示为

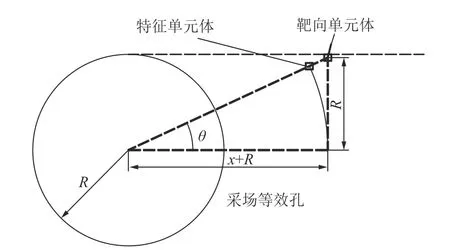
图4 特征单元体示意Fig.4 Schematic diagram of characteristic unit

将式(4)代入式(3)，可以得到特征单元体的应力表达式，以特征单元体的应力状态来定义轴线上距离孔心x+R处的应力环境。将特征单元体切向应力视为距离孔心x+R处的垂直应力，径向应力视为距离孔心x+R处的水平应力，剪应力视为距离孔心x+R处的剪应力。通过莫尔圆应力圆，将特征单元体的应力状态进行转换，即可得到x+R处的主应力方向，转换过程如图5 所示。图5 中β为最大主应力与垂直方向的夹角，即为主应力旋转角度，与式(2)中的α之间的关系式为

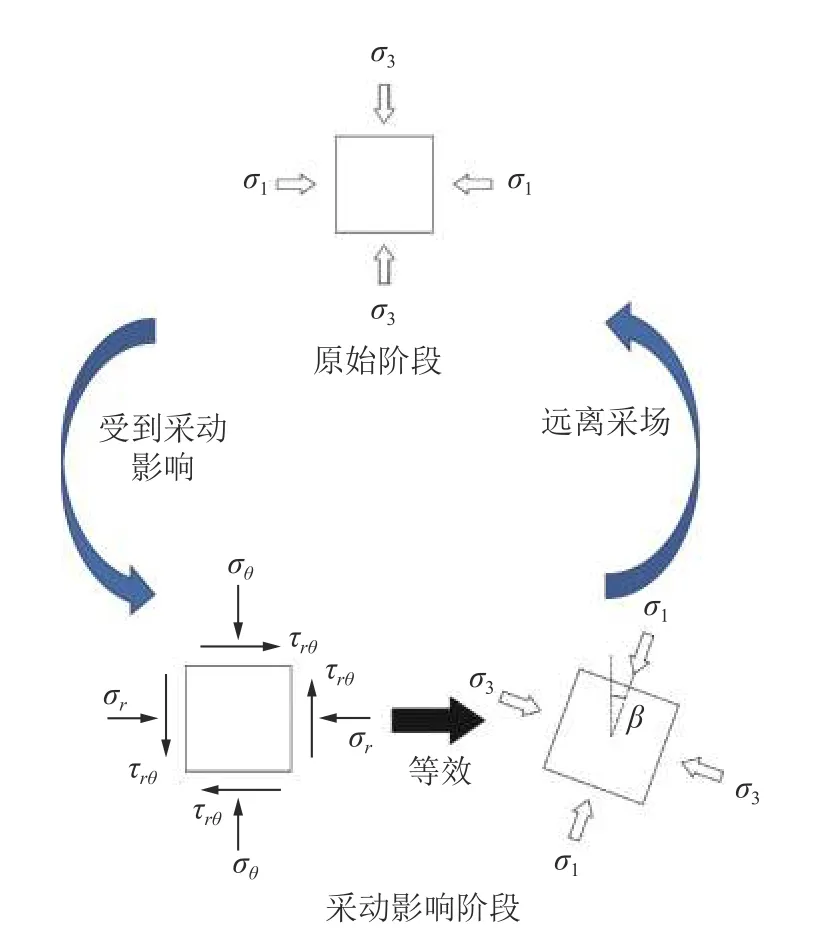
图5 特征单元体主应力旋转示意Fig.5 Schematic diagram of principal stress rotation of characteristic unit

β可以由莫尔应力圆求得，计算公式为

当β为顺时针转动时取正，逆时针转动时取负，σθ与σr以压应力为正，τrθ逆时针为正。

将式(3)、(4)、(6)联立，即可得到特征单元体的主应力角度，可将其视为距离等效孔圆心为x时，采场采动影响所造成的主应力的旋转角度。主应力旋转角度表达式为

2.2 主应力旋转角度影响因素分析

由式(8)可以看出，主应力旋转角度的影响因素共有2 个：等效孔半径R、侧压系数η。

2.2.1 等效孔半径对旋转角度的影响(1)侧压系数大于1。

由于埋深较浅时水平方向地应力一般大于垂直方向地应力，故定义初始条件为埋深300 m，即垂直应力为7.5 MPa，侧压系数取1.5，由式(8)计算出等效孔周边主应力旋转角度随着距离增加的变化，具体结果如图6 所示。

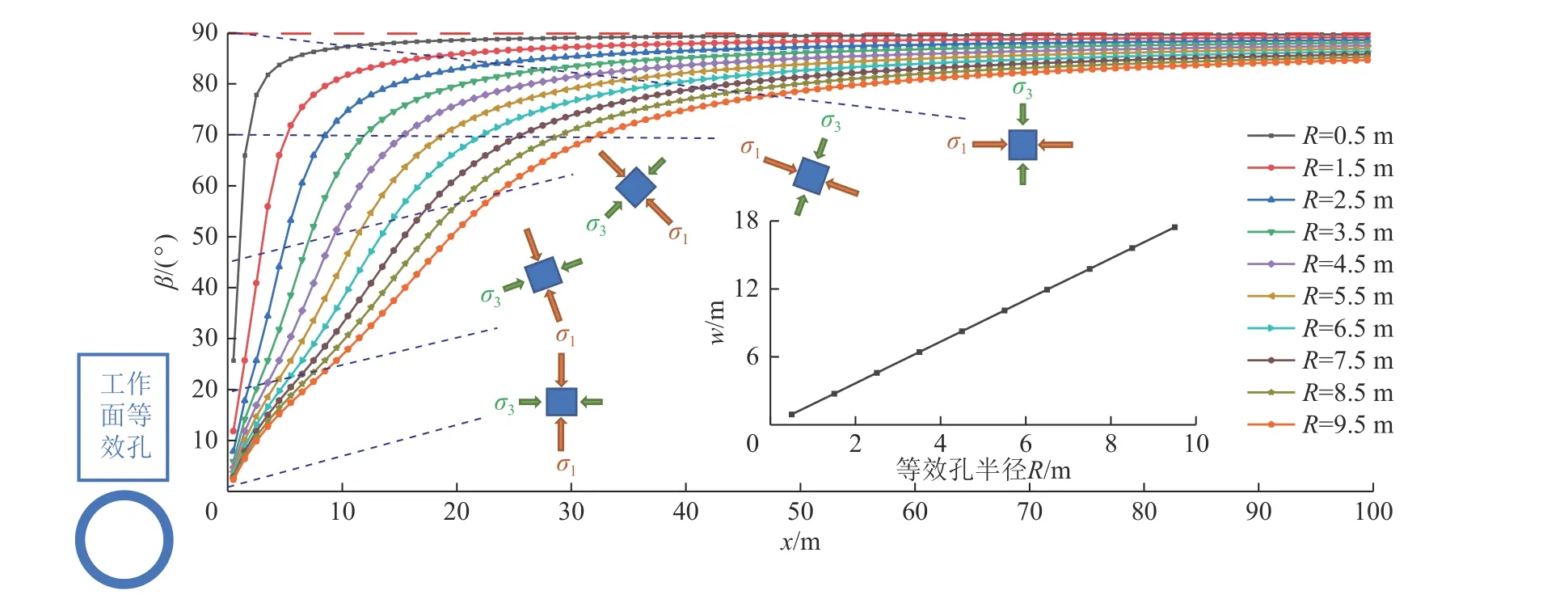
图6 η=1.5 时等效孔半径与主应力旋转角度Fig.6 Schematic diagram of equivalent hole radius and rotation angle of principal stress when η=1.5

从图6 可知，随着等效孔半径的增大，当距离等效孔孔边相同距离时，主应力旋转角度β会呈现减小的趋势。当旋转角度为45°时，随着等效孔半径的增大，其对应的x会逐渐增大。随着等效孔半径的增大，主应力旋转的速度会呈现减缓的趋势，前期主应力旋转迅速，会在较短距离内完成45°的偏转，当偏转角度到达一定值时，主应力偏转的速度会降低，并逐渐趋近于最终值。主应力旋转角度的最终值由侧压系数来决定，若侧压系数大于1，则最终值为90°；若侧压系数小于1，最终值为0°。主应力旋转角度为45°是一个分界值，当旋转角度为45°时，塑性区碟叶位置由巷道4 个边角旋转至巷道的顶底板中间与帮部中间，巷道顶板失稳的风险较大。因此，研究主应力旋转45°的位置对巷道围岩塑性区的影响位置的判定有着重要意义，笔者定义主应力旋转角度为45°的位置为w。当主应力旋转角度为45°时，即可得到关于w的四次隐性方程，即

由式(9)可知，w与等效孔半径和测压系数的取值有关。令测压系数为1.5，对不同等压孔大半径下的w进行求解，计算结果见表1，w与R的关系如图6所示。

表1 不同等效孔半径 R 对应的wTable 1 w of different equivalent hole radius R

由表1 与图6 可知，w与等效孔半径R呈现线性增加关系。等效孔半径R越大，相应的w越大，即主应力旋转的速度越慢；等效孔半径R越小，相应的w越小，即主应力旋转的速度越快。

等效孔半径的取值由实际工程地质条件、采高、开采方式、顶板处理方式、工作面支护能力等一系列因素决定，具体取值的方式还目前并不能给出一个完整的解析式，但可等效孔半径的取值应当依据采动的剧烈程度而定。当工程采动状况剧烈时，例如工作面采高较高，则采动所造成的影响范围很大，此时工作面的等效孔取值必然较大，w也较大；当工程采动状况不剧烈时，例如工作面采高较低，此时采动影响范围较小，工作面等效孔的取值必然较小，w也较小。

(2)侧压系数小于1。

矿井埋深较深时水平方向构造应力减弱，部分矿井垂直方向应力大于水平方向应力，此时侧压系数将小于1，故定义初始条件为埋深1 000 m，即垂直应力为25 MPa，侧压系数为0.8，通过式(8)计算出等效孔周边主应力旋转角度随距离增加的变化，如图7所示。

图7 η=0.8 等效孔半径与主应力旋转角度示意Fig.7 Schematic diagram of equivalent hole radius and rotation Angle of principal stress when η=0.8

由图7 可以看出，侧压系数小于1 时，主应力的旋转角度呈现先增大后减小的规律，且存在一个峰值，这个峰值由侧压系数决定，当到达峰值之后，主应力旋转角度会逐渐减小。但随着等效孔半径的增加，这个峰值的影响区间会逐渐扩大，即表明主应力角度旋转的范围会逐渐扩大。

通过对侧压系数大于1 和小于1 两种情况下变化等效孔半径得到的主应力旋转角度分析可以看出，无论初始侧压系数多大，等效孔半径越大，则主应力旋转角度的影响区间越大，主应力旋转角度变化至最终值的速度越慢，采场等效孔的半径与采场的实际影响效果成正比。

2.2.2 侧压系数对旋转角度的影响

煤层埋深较浅时，水平方向构造应力较强，其值大于垂直方向的应力，即侧压系数大于1。煤层埋深较深时，此时地表的地质构造作用较弱，部分矿井水平应力将小于垂直方向应力，即侧压系数小于1，侧压系数的大小对主应力的旋转角度有着重要的影响。

令等效孔半径R为2.5 m，利用式(8)求得主应力旋转角度。

(1)侧压系数小于1 时，主应力旋转角度随距离变化如图8 所示。由图8 可知，侧压系数小于1 时，主应力旋转角度先增大后减小，最大主应力趋近于垂直方向，主应力的旋转角度始终小于45°，即表明最大主应力方向基本以垂直方向为主。

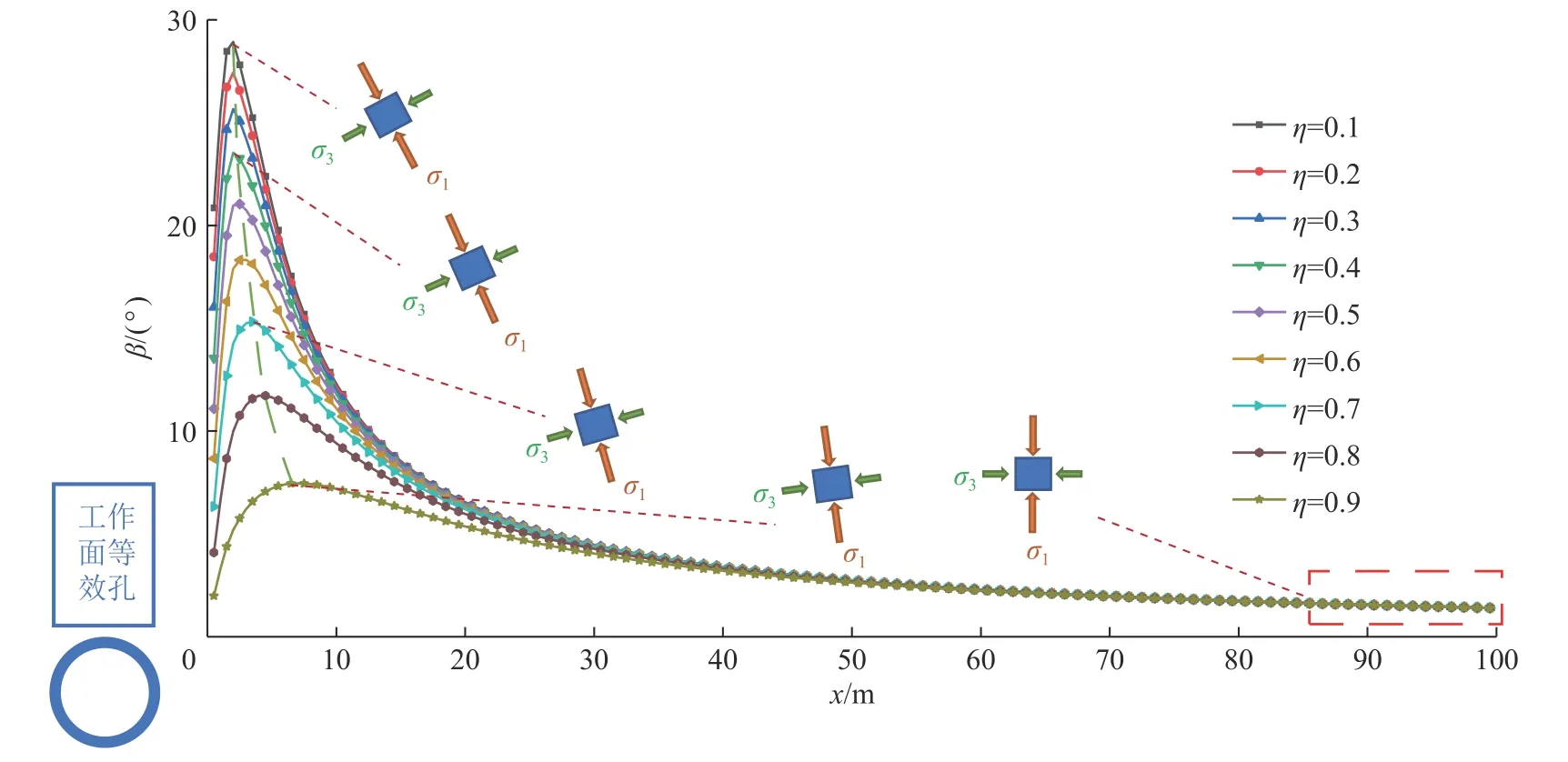
图8 R=2.5 m、η <1 时旋转角度示意Fig.8 Schematic diagram of rotation Angle of principal stress when R=2.5,η <1

(2)当侧压系数大于1 时，主应力旋转角度如图9所示。由图9 可知，侧压系数大于1 时，主应力旋转角度随着x的增大而增大，增大的速度呈递减的趋势。侧压系数越大，主应力旋转越快，旋转角度增加越快；侧压系数越小，主应力旋转越慢，旋转角度增加越慢。利用式(9)对w求解，结果见表2，w与η的关系如图9所示。

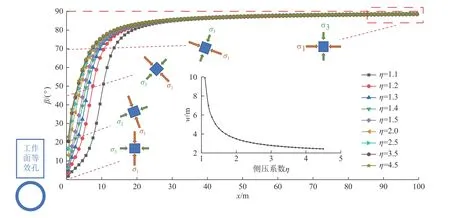
图9 R=2.5 m、η >1 时旋转角度示意Fig.9 Schematic diagram of rotation Angle of principal stress when R=2.5,η >1

由图9 可知，随着侧压系数的增大，w呈减速降低的趋势，且当侧压系数增大到一定值后，w无限趋于一个恒定值，这个恒定值由等效孔的半径决定。当侧压系数减小到一定值时，w呈现加速上升的趋势，且侧压系数越小，w越大，表示主应力旋转45°的位置距离采场越远。这表明侧压系数大于1 时，侧压系数越小，采场采动影响使主应力发生偏转的范围越广。

综上可以得到：①等效孔的半径与采场实际影响效果成正比，等效孔越大，则表明采场的影响效果越广，主应力旋转角度的影响区间越大，主应力旋转至最终值的过程越缓慢。②侧压系数大于1 时，最大主应力方向从竖直方向转向水平方向，且w与等效孔半径成正比；侧压系数小于1 时，最大主应力方向先由竖直方向向水平方向偏转一定角度，之后回到垂直方向。③当采场等效孔半径确定时，即采场的影响范围确定，若侧压系数小于1，则侧压系数影响主应力旋转角度峰值；若侧压系数大于1，则侧压系数会影响w。

3 等效孔模型验证与采场侧方主应力旋转角度规律分析

3.1 数值模型的建立

布尔台矿井是神华神东煤炭集团的大型矿井，首采的2-2煤层为近水平煤层，煤层埋深约300 m，平均倾角1.5°，采用盘区式布置方式。其中22205 工作面长度303 m，煤层平均采厚为3.5 m，一次采全高，并采用全部垮落法处理采空区。

为了研究采场侧方的主应力旋转特征，并验证等效孔模型的有效性，利用FLAC3D数值模拟软件，以布尔台矿井的工程地质条件作为模型基础[8]，构建三维数值模拟模型，模型尺寸为600 m×600 m×100 m(长×宽×高)，模型上部施加γh=25 kN/m3×220 m=5.5 MPa的垂直方向载荷用以模拟上覆岩层与松散体自重，模型四周采用滚筒支撑约束，底部采用固定约束。模型初始侧压系数沿Y轴方向为1.5，X轴方向为1，利用initialize-stresses 命令进行初始平衡，模型三维图像如图10 所示。

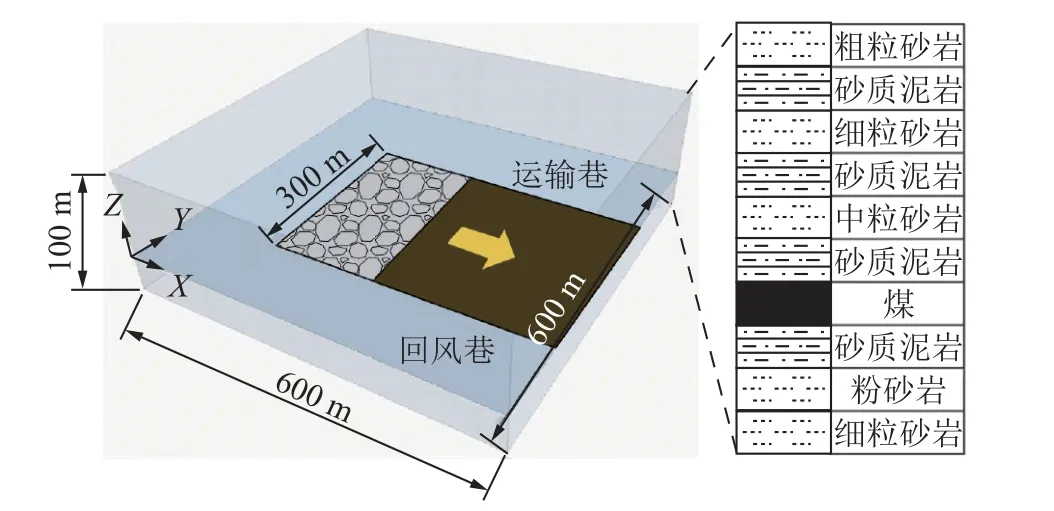
图10 三维数值模拟模型Fig.10 Three dimensional numerical simulation model

为了简化三维模型，模型中22205 工作面长度设为300 m，推进长度设为400 m，并对工作面侧方100 m范围内的网格进行加密处理，以便于后续对采场侧方主应力旋转角度展开研究。

根据现场推进速度，开挖过程中每10 m 循环平衡一次，每次平衡均保留实验数据。模拟过程中岩层采用Mohr-Coulomb 本构模型，在岩石力学实验基础上对岩石参数进行修正，得到岩层力学参数。工作面实际开采后采用全部垮落法处理采空区，在模型中利用双屈服本构模型对采空区进行充填以模拟垮落带岩体重新压实的过程，岩石力学参数与垮落体力学参数见表3、4。

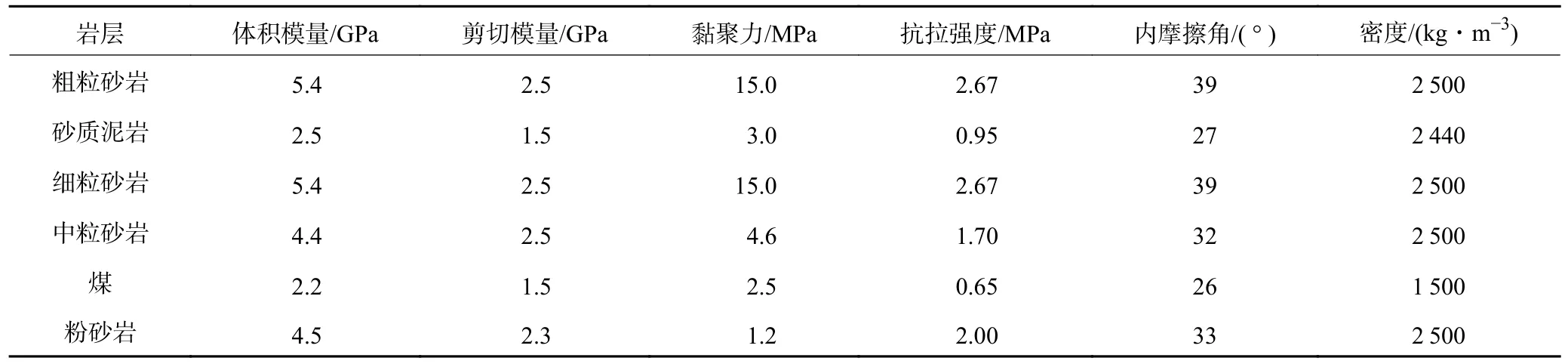
表3 模型岩石力学参数Table 3 Model rock mechanics parameters

表4 垮落带双屈服本构模型Table 4 Material mechanics parameters for caved rock in Double-yield

3.2 数值模型主应力旋转角度

3.2.1 采场侧方主应力旋转一般规律分析

为了验证采场侧方主应力角度旋转的现象是普遍存在的，分别选定推进长度为170、180、190、200 m，对工作面侧方100 m 范围内的单元体应力数据进行提取分析，利用式(8)计算采场侧方主应力旋转角度，如图11 所示(x为单元体与运输巷的距离)

由图11 可知，当推进到不同距离时，采场侧方的主应力角度随着距离变化均发生了偏转，且偏转的过程相似，整体旋转的规律一致，这表明采场侧方主应力角度旋转是普遍存在的一种现象，推进到不同阶段采场侧方均会发生主应力角度的旋转，s轴代表测线与开切眼处的距离。

由于沿模型Y轴方向的的侧压系数大于1，采场侧方主应力旋转角度将由小到大逐渐增加到90°的最终值，主应力角度旋转的速度由快而慢。

3.2.2 理论旋转角度与数值模拟对比分析

本节以推进长度为200 m 时工作面侧方的主应力旋转角度的模拟数据作为对比对象，数值模型中沿模型Y轴方向的侧压系数已知为1.5，需要选定一个合适的等效孔半径R用以描述工作面侧方的主应力旋转角度。

等效孔半径R的取值并没有明确的解析表达式，最合适的取值将根据理论数据与模拟数据比对得到。由等效孔半径为1.00 m 开始，间隔0.25 m 递增，对理论旋转角度进行计算，经过与模拟数据的比对，半径位于1.00～2.00 内的等效孔与模拟数据吻合度较低，而2.00～3.00 内的等效孔吻合度较高，故选定等效孔半径分别为2.00、2.25、2.50、2.75、3.00 这5 种情况，与模型模拟数据进行对比，如图12 所示。

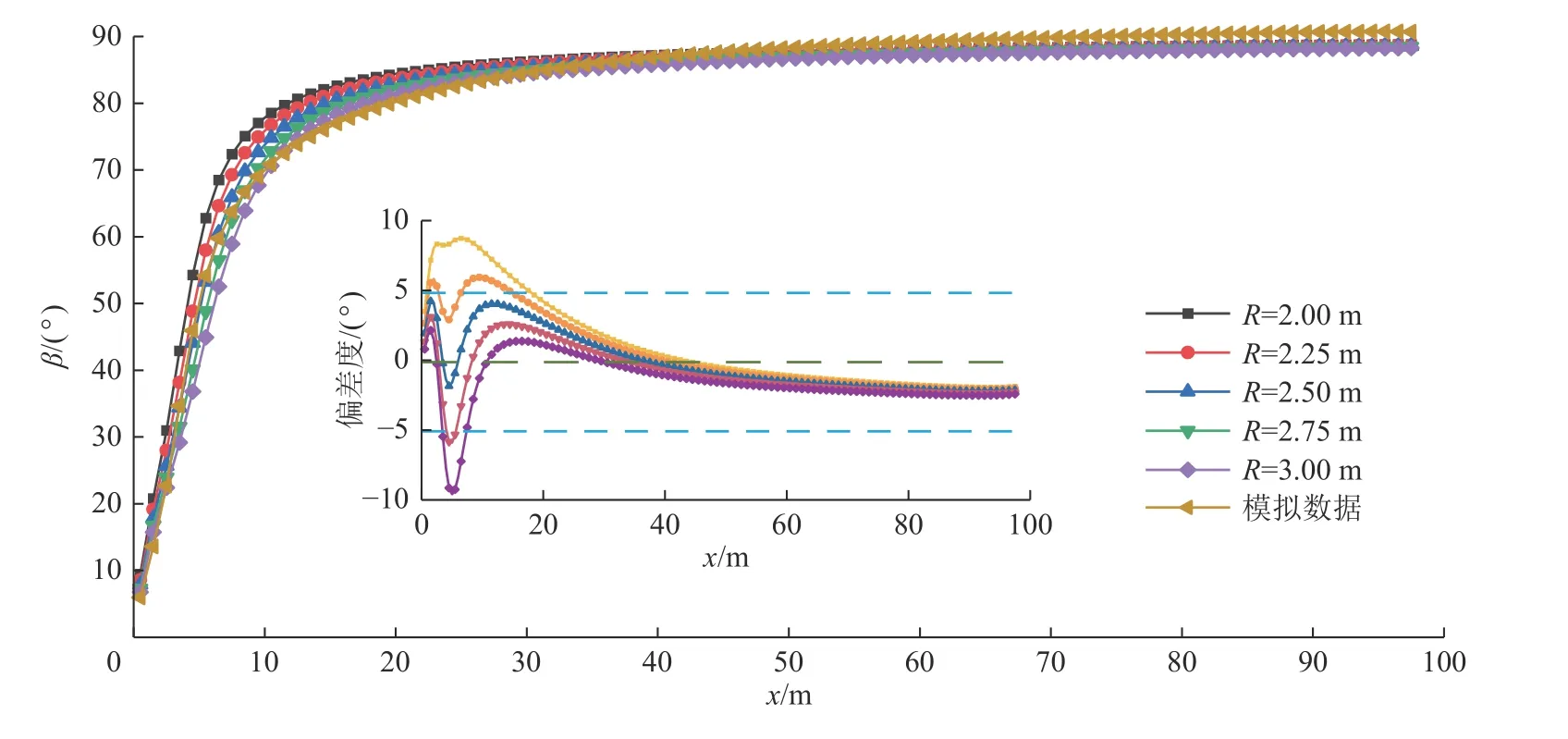
图12 模拟值与理论值对比Fig.12 Comparison diagram of simulated data and theoretical data

将理论数据与模拟数据的差值定义为偏差度，研究3 个等效孔半径下的理论数据与模拟数据的偏差程度。由图12 的偏差度可知，当R=2.50 m 时，理论计算的旋转角度与实测旋转角度的偏差度较小，偏差度均在4°以内，随着距离的增加，到达一定值时，偏差度趋向于一个恒定值，但均在4°以内，并不影响主应力角度的大致方向判定。由上述研究可以得出，采场等效孔的理论模型能够很好地表征采场侧方的主应力旋转的特征，即使存在一定的偏差，但是并不影响主应力大致方向的判定。

3.2.3 轴向等效孔拟合及标志线确定

由3.2.2 节可知，将工作面开采对侧方的影响程度简化为一个等效孔，可以找到一个合适的等效孔半径R，使得模拟旋转角度与式(8)计算所得的理论旋转角度偏差度较小，即认为存在半径为R的等效孔来描述工作面侧方的主应力角度旋转状况。

对于采空区而言，由于采空区内尚未形成有效的支承应力，整体应力水平偏低，采空区垮落区域相对于采空区侧方煤体是一个卸压区域。对于工作面前方的巷道侧方煤体而言，受到工作面扰动的程度随着与工作面之间的距离增大而逐渐减小，在距离工作面较近的位置，巷道侧方煤体受到工作面影响较大，巷道对于其侧方煤体是一个卸压区域。因此，对采空区侧方的煤体以及工作面前方的巷道侧方煤体而言，采场对其的影响都可以简化为一个等效孔，即可以选取等效孔半径R，以此半径的等效孔来表征侧方煤体的主应力旋转特征。

当模型推进到200 m，在工作面前方和后方选取10 条测线，通过命令提取测线上的单元体应力数据，利用式(8)计算出测线上的单元体主应力旋转角度，并选取等效孔来描述测线上的应力旋转角度，s为测线与开切眼处的距离，如图13 所示。

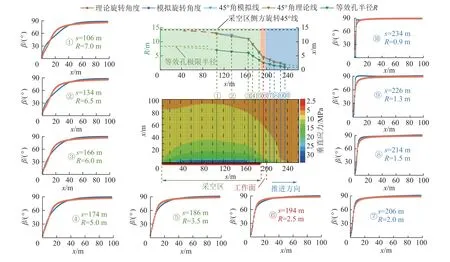
图13 推进方向采动影响等效孔拟合Fig.13 Fitting diagram of equivalent hole influenced by mining in advance direction

图13 中绿色实线、蓝色实线、红色实线代表测线位置。由图13 可见，模型中测线上的主应力旋转呈现出一定的规律，沿工作面推进方向整体呈旋转加速的趋势。由图13 与图6 相比较可知，由采空区到工作面前方测线上的应力旋转变化规律与等效孔半径的缩小变化规律相同。对每一条测线，都选取等效孔进行旋转规律的描述，模型中每条测线上的旋转角度曲线与理论计算的旋转角度曲线如图13 的外侧框中所示。由图框中的不同测线处的模拟旋转角度曲线和理论旋转角度曲线对比可知，每条测线处都可以选出半径为R的等效孔，使得模拟旋转曲线与理论旋转曲线基本一致，整体差距非常小，即可以用此半径的等效孔来描述采空区、工作面或工作面前方的侧方煤体中的主应力旋转情况。将不同测线处的等效孔半径进行提取，绘制曲线如图13 中绿色线所示。

由采空区到工作面前方的过程中，等效孔的半径呈减小的趋势，即表征着采场采动影响的减弱。当到达工作面前方距离工作面一定距离时，等效孔半径则趋向于一个稳定值，说明此区域的侧方煤体没有受到采动影响。而随着深入采空区，等效孔半径则会逐渐增大，说明采空区内尚未形成有效支承，采空区对侧方煤体产生了较大的影响，影响程度较高则等效孔半径较大。但是采空区的影响程度有一定的限度，即等效孔的半径最终会趋于一个极限半径，这个极限半径代表着采空区对侧方煤体的最终影响程度。

将每一条测线上旋转45°的位置进行提取，即可得到一条旋转45°标志线，即如图13 中淡蓝线所示。旋转45°标志线以内代表主应力旋转小于45°，而旋转45°标志线以外则代表主应力旋转大于45°，旋转45°标志线是衡量采空区或工作面对侧方的煤体的影响范围的一个指标。将每条测线处的等效孔代入式(8)，即可计算出每条测线处理论旋转45°的位置，即得到旋转45°理论线，如图13 中棕色线所示。由旋转45°模拟线和旋转45°理论线对比可知，2 者差距非常小，即利用45°理论线可以较好地反映模型中采空区与工作面侧方煤体中的应力旋转情况。

综上所述，可以得到：①模型中的工作面前方、工作面和采空区的侧方煤体中的主应力旋转规律均可以用一个等效孔周边的主应力旋转进行描述。每个位置都可以找到半径为R的等效孔，使得此半径下的等效孔周边的理论旋转角度曲线和实际旋转角度曲线相吻合且偏差度较小。②工作面开采不仅会造成侧方煤体应力在数值上集中，也会造成工作面前后一定范围内的侧方煤体中主应力方向发生旋转，这种旋转在深入采空区一定范围内之后将趋于稳定阶段。

4 结论

(1)采场开采不仅会导致侧方煤体应力在数值上集中，也会使得主应力方向发生变化。这种主应力方向的变化是渐变的过程，在受到工作面采动影响时开始变化，在距离工作面一定距离的采空区侧方中则趋于稳定。

(2)提出了采场等效孔的理想化理论模型，确立了计算采场侧方主应力旋转程度的思路。当侧压系数小于1 时，最大主应力由垂直方向先旋转至最大角度，随后会回转至垂直方向；当侧压系数大于1 时，最大主应力由垂直方向逐渐旋转为水平方向。主应力具体旋转过程由原始状态的侧压系数决定。

(3)等效孔半径表征采场侧方主应力旋转的范围。采场影响范围越大，则等效孔半径越大，应力旋转的区间越广。采场影响范围越小，则等效孔半径越小，应力旋转的区间越窄。在距离工作面不同位置都可以找到合适的等效孔半径用以描述采场侧方主应力旋转情况。

(4)当侧压系数小于1 时，侧压系数会对采场侧方主应力旋转角度的峰值产生影响，侧压系数越小则主应力旋转角度的峰值越大。当侧压系数大于1 时，侧压系数则只会影响主应力角度旋转的速度，最终最大主应力都将旋转至水平方向。

(5)当初始侧压系数大于1 时，提出了主应力旋转45°隐性方程，可以对采空区侧方旋转情况进行判定。若处于45°线以内，则最大主应力偏于垂直方向；若处于45°线以外，则最大主应力偏于水平方向。