薄规格带钢层流冷却过程在线温度模型

潘 瑜 李海军 王 麟 宁新禹 李睿昊

(东北大学轧制技术及连轧自动化国家重点实验室)

随着钢铁制造市场的激烈竞争，薄带产品以其生产周期短、性价比高的优势，越来越受到钢铁制造商们的重视[1]。热轧带钢生产过程中层流冷却对产品的组织性能有很大的影响，然而薄规格带钢运行速度高、温降快，为了满足冷却过程实时性的要求，在线温度模型需要有较高的计算效率[2-5]。带钢轧后冷却过程的在线控制，通常是按一定长度将带钢划分为多个样本段，对每个样本段进行单独地跟踪控制。对于薄规格带钢，为了满足系统响应时间的要求，样本段的长度一般为一组层流冷却集管的两倍到三倍，因此通过提高温度模型计算效率来缩短样本段的长度，有利于薄规格带钢卷取温度控制精度的进一步提升。

温度计算模型作为层流冷却过程控制系统的基础和核心，直接决定着整个冷却过程的控制精度[6]。文章以某钢厂热连轧带钢层流冷却过程为研究对象，建立了显式格式和隐式格式两种有限差分温度模型，探讨了不同差分格式以及网格划分方法对模型计算效率的影响，提出了一种具有快速响应特性的在线温度控制模型。

1 控制冷却温度模型

1.1 传热理论模型

薄规格带钢冷却过程沿长度方向和宽度方向的散热量相对于厚度方向来说较小，可以忽略，同时相变产生的热量可以计入相应冷却过程钢板的比热内，所以可把带钢的冷却过程看作是无内热源的一维非稳态导热过程[7-8]：

(1)

式中：T为带钢温度，℃；τ为时间，s；λ为带钢导热系数，W/(m·℃)；ρ为材料密度，kg/m3；c为材料比热容，J/(kg·℃)；x为带钢厚度方向的坐标。

初始条件为带钢精轧出口的温度分布：

τ=0,T=T0

(2)

边界条件的处理则可以根据带钢在实际冷却过程中的状态确定，采用空冷辐射和水冷对流已知的第三类边界条件：

(3)

式中：α为带钢表面换热系数，W/(m2·℃)；Tf为带钢表面冷却介质温度，℃。

层流冷却条件下的水冷换热系数模型为[9]：

(4)

式中：Z12，Z2为换热系数自学习项；a1，a2，a3，V0为模型参数；V为带钢分段实时速度，m/s；Vbase为精轧穿带速度，m/s；h为带钢厚度，m；Tw为水温，℃。

空冷条件下的换热系数模型为：

α=kair·ε·σ·[(T+273)2+(Ta+273)2]·[(T+273)+(Ta+273)]

(5)

式中：kair为修正系数；ε为钢板黑度系数；σ为斯蒂芬—波尔茨曼常数；Ta为空气介质的温度，℃。

1.2 导热方程离散化

有限差分法求解带钢在冷却过程中的温度场时，将微分方程表示为定义在离散节点上的差分方程，由微分方程体现的节点间的数值关系，通过给定的边界条件和相邻节点间的差分关系计算出未知边界上的数值。显式格式和隐式格式差分法的主要区别在于替代计算微分方程的差分方程中对微分项的离散化近似表示不同[10-12]。

显式差分格式直接利用当前时刻节点的温度计算，导热微分方程用向前差分方程表示：

(6)

显式格式差分方程进行数值计算时，只要知道初始时刻不同位置的值，就可以直接利用迭代法快速求解[13]，即可获得不同时刻的带钢温度场，但为了确保数值解的收敛性和稳定性，时间步长必须满足条件Δτ≤(Δx)2/(2α)。

采用隐式差分格式时，温度用向前差分方程表示，空间二次微商使用τk+1时刻的二次中心差商置换：

(7)

隐式差分具有无条件稳定性，时间残项为一阶，空间上为二阶残项[14]。不能由一个格点数值直接得出下一时刻3个未知的格点数值，需要列出各个节点间的所有关系，然后采用追赶法求解方程组，即可得到带钢不同时刻的温度场。

1.3 网格划分的方法

国内某2 150 mm热轧线层流冷却温度模型采用等厚度方法划分网格，然而在实际冷却过程中，表面网格间温差较大，芯部网格间温差较小。因此采用变厚度的网格划分方法，有望在保证计算精度的前提下，提升温度模型的计算效率。

高斯网格划分各节点厚度，从带钢表层到中心逐渐增加，沿厚度中心线两侧对称分布。节点实际位置的厚度可以通过轧件的总厚度乘以各节点的相对坐标获得，各节点的相对坐标计算公式：

(8)

假设上下表面是对称冷却的过程，以带钢厚度的一半为研究对象，各节点厚度从带钢中心至表层逐渐减小，且相邻两节点间距离与d的取值有关。自然对数划分网格计算公式为：

xi=elnh-i·d,(0≤i≤n-1)

(9)

不同网格划分方法节点的相对厚度如图1所示，相对厚度是指两相邻节点相对坐标的差值，可以看出，自然对数划分方式与高斯网格划分和等厚度划分相比，在带钢边部(节点1处)的网格划分更加密集，而接近中心位置(节点4处)的网格划分更加稀疏。

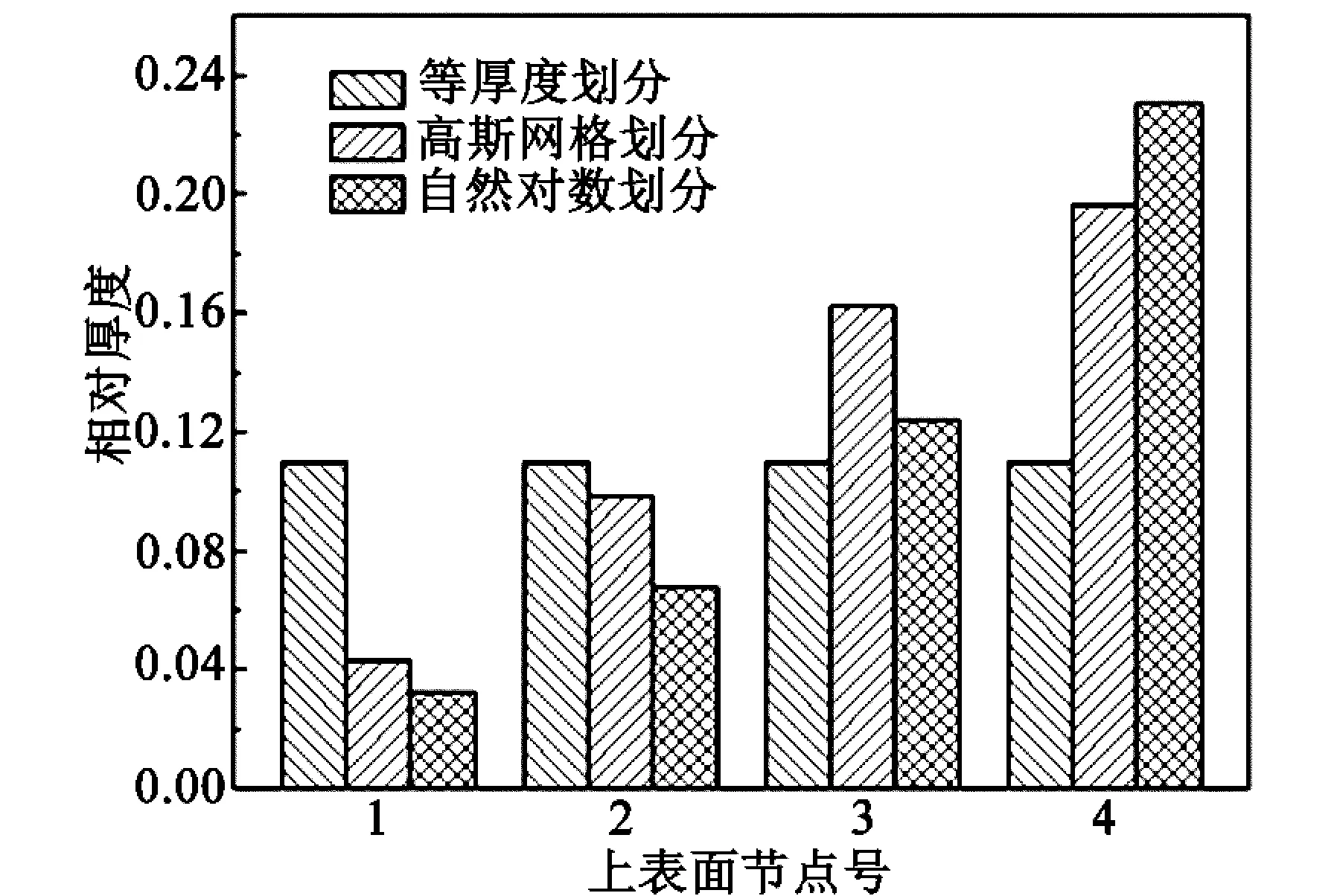
图1 网格划分节点的相对厚度

2 冷却设备及工艺条件

以某钢厂2 150 mm热轧生产线为研究对象，其轧后冷却设备布置见图2。冷却区全长106 m，共19个集管组依次为前部超快冷段、主冷段、后部超快冷段，精冷段。其中主冷段每组6根集水梁，精冷段每组12根集水梁，超快速冷却段喷嘴数量每组为12根。带钢从精轧机出口经过层流冷却区达到目标卷取温度，最后进行卷取。

采集现场头部样本的冷却工艺参数，轧制钢种为Q235B，厚度规格为2.5 mm，穿带速度为11 m/s，环境温度为25 ℃，水温为29.3 ℃，实测精轧出口温度为880 ℃，实测卷取温度为620 ℃，集管组总流量为2 154 m3/h。Q235B的热物性参数如表1所示[15]，密度、比热和导热系数随温度变化，非节点温度对应的热物性参数可通过线性差值计算得到。

表1 Q235B的热物性参数

3 计算结果与分析

3.1 差分格式对模型效率的影响

根据已知的工艺条件，对导热微分方程进行差分处理并求解。显式格式和隐式格式差分温度模型均采用自然对数的网格划分方法，厚度方向取9个节点，计算得到带钢冷却过程温度分布情况见图3。带钢从精轧机出口经过层流冷却区到达卷取机入口，由空冷区进入水冷区，中心与表面的温差逐渐增大，由水冷区进入空冷区，中心与表面的温差逐渐减小，骤冷后表面与中心的温差导致带钢内部的热量传向表面，出现表面返红现象。隐式格式计算得到的上表面卷取温度为621.45 ℃，显式格式计算得到的上表面卷取温度为618.31 ℃，两种差分格式求得温度曲线十分接近，均能较好的预测卷取温度。隐式格式具有无条件稳定性的优点，时间步长的选取更加宽泛，而显式格式的时间步长必须满足稳定性条件，通常要求时间步长足够的小。温度模型中隐式格式时间步长选取为0.5 s，显式格式时间步长为0.1 s，图4为不同节点数下两种差分模型计算时间。可以看出，隐式格式计算用时远小于显式格式，且随着节点数划分增加，隐式格式计算效率优势更加明显。因此，针对薄规格带钢的层流冷却过程，可以采用隐式差分格式，在保证计算精度的前提下，采用较大的时间步长划分，来提高温度模型的计算效率。

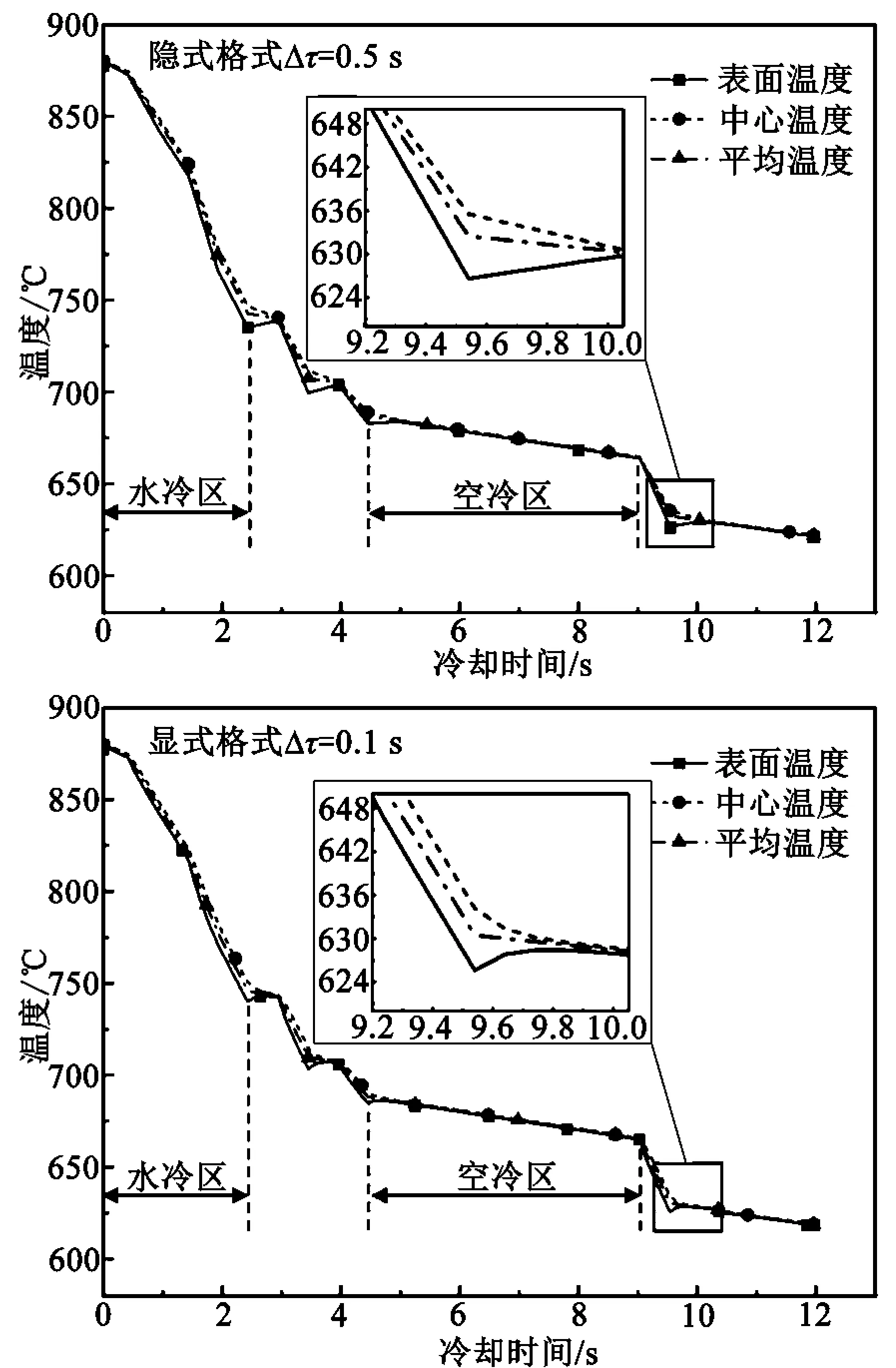
图3 有限差分法计算带钢温度分布

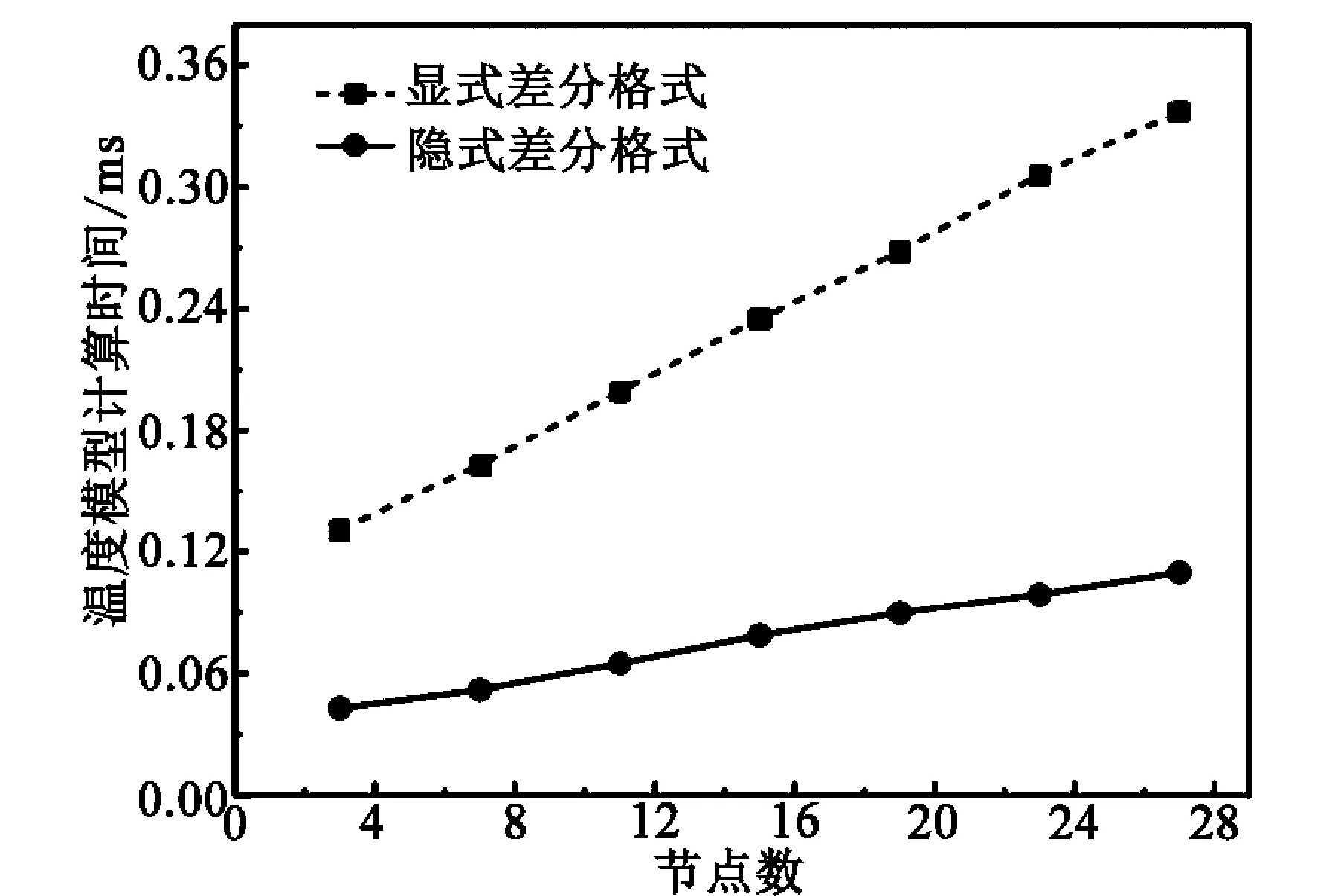
图4 不同节点数差分格式计算时间

3.2 网格划分对模型效率的影响

选取隐式差分模型，时间步长取0.5 s，分别采用等厚度划分、高斯网格划分和自然对数划分网格，对带钢冷却过程卷取温度进行计算，得到不同节点数下网格划分方式的相对误差见图5。由图可知，在相同节点数下，自然对数划分网格的温度模型计算精度高于高斯网格划分和等厚度划分。在确保相对误差小于0.25%的条件下，等厚度划分需要13个节点，高斯网格划分需要9个节点，自然对数划分需要7个节点，其对应的运行用时分别为0.076、0.056和0.051 ms，说明在相似计算精度的条件下自然对数划分网格计算效率最高。

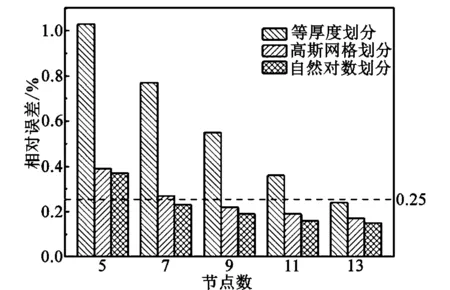
图5 不同网格划分计算相对误差对比

4 结论

(1)采用有限差分法建立显式格式和隐式格式两种差分模型对温度场进行求解，均能准确反映冷却过程温度分布情况。显式格式的震荡性对解有影响，要求时间步长的选取较短，使得温度模型计算耗时多；隐式格式具有无条件稳定性，在确保计算精度的同时，可以通过增大时间步长，提高模型计算效率。

(2)采用不同的网格划分方式对带钢冷却过程卷取温度进行计算，得到不同节点数下网格划分方法的相对误差，自然对数划分网格的温度模型计算精度高于高斯网格划分和等厚度划分。

(3)在确保相似计算精度的条件下，自然对数划分网格计算效率最高。因此，可以采用自然对数划分网格节点，使得换热条件复杂的上、下表网格细，内部网格粗，有利于满足薄规格带钢层流冷却在线温度模型的高计算效率要求。