一种基于部分威力试验数据的飞散角计算方法

李泓江，曹 涛，胡鹏顺，蔡辰忱

(63876部队，陕西 华阴 714200)

0 引言

威力试验主要包括破碎性试验、扇形靶试验和静态飞散角试验,一般用于评定和研究杀伤爆破弹丸(简称杀爆弹)利用爆炸产生的高速破片与爆炸冲击波对目标的毁伤[1],其中破片杀伤效应占据主导地位[2]。

破碎性试验是测定榴弹破片质量分布的一种有效试验方法。通常将弹丸放在一个空容器的中央,周围放置使破片减速的介质,爆炸后回收破片并按质量分组,从而得到在不同质量范围内的破片数[3]。文中使用的是水介质破碎性试验水池回收破片,使用酒精清洗后晾干称重。扇形靶试验是测试弹丸击穿破片杀伤半径的一种常用试验方法[4-5],爆炸后破片向四周飞散并穿过松木靶面,通过统计松木靶内破片穿透数,得出击穿破片杀伤半径。静态飞散角试验是战斗部爆炸后,在战斗部轴线平面内,以质心为顶点所作的包含有效破片90%的锥角[6],也就是破片飞散途中包含有效破片90%的两线之夹角。

目前国内外对飞散角的计算仿真和试验测试已有较多的研究。申景田等[7]采用直线排列的钢靶板测量破片数量和空间分布,统计出占总破片数85%以上的杀伤带,根据破片着靶位置和弹丸起爆点位置推算出飞散角;刘武等[8]采用ANSYS/LSDYNA建立有限元模型,结合流固耦合算法,对破片飞散角进行研究;李茂等[9]通过开展TNT装药驱动轴向预制破片飞散试验,获得预制破片飞散角参数,然后运用LS-DYNA软件对驱动过程进行数值模拟;MOXNES等[10]对战斗部钢壳的断裂和飞散进行了试验,并采用不同模型进行模拟研究。经统计分析,目前基于破碎性、击穿破片杀伤半径等威力试验数据,计算出飞散角方法的相关文献较少。

文中以杀爆弹为样本,开展试验获得威力试验数据,计算不同质量级别破片的终点速度及飞行距离,用Origin软件拟合破片飞行距离与破片数的曲线。通过杀伤密度建立飞散角与击穿破片杀伤半径之间的关系,基于部分威力试验数据计算飞散角理论值。理论结果与试验结果进行对比分析。

1 破片飞行理论

1.1 破片终点速度

根据破片质量mf,杀伤标准动能E,可以得满足动能要求的最低速度vL:

(1)

1.2 破片初始速度

破片初始速度(初速)是衡量战斗部杀伤作用的重要数据,因此进行理论计算时要尽可能的准确。影响破片初速的因素很多,为简化问题,做以下几点假设:

1)假定爆轰是瞬时的,破片加速为瞬时;

2)爆轰产物线性分布忽略爆轰产物沿装药轴向飞散;

3)壳体为等壁厚且爆炸后形成的破片具有相同的速度;

4)忽略壳体破裂阻抗,炸药能量全部转化为破片动能和爆轰产物动能,没有能量耗散;

5)不考虑端部效应[11]。

对于文中所要研究的圆柱形弹丸,应使用哥耐(Gurney)公式[12]:

(2)

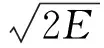
1.3 破片飞行距离

破片的运动方程[13]为:

(3)

(4)

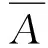
虽然cx在实际中是变化的,但在某一速度区间内可近似用一常数表示。对大部分破片的几何形状来说,cx随速度变化的规则相似。为了限制区间划分对计算结果产生的影响,在马赫数取0.1～20的范围内分为14个区间。vai和vei表示第i区间速度上、下限。

假设x=0时,速度为vf0,则第i区间破片飞行的距离xi,可根据式(3)求出:

(5)

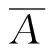
(6)

式中Kp为破片形状系数。破片形状系数主要通过试验方法来获取,对于球形、方形预制破片,其Kp取3.07～3.09;对于柱形预制破片,其Kp取3.35;对于菱形预制破片,其Kp取3.2～3.6;对于长方形预制破片,其Kp取3.3～3.8;对于不规则破片,其Kp取4.5～5.0。通过观察杀爆弹样本的破碎性回收破片,大部分破片为不规则形状,极少部分破片为菱形或长方形,因此,此处破片形状系数Kp取4.5(不规则)。

处理破碎性试验威力数据,按照相关标准统计出每一质量范围内的破片数,绘制破片质量分布曲线、破片累积个数与破片质量关系曲线。

通过上述计算,得出某一质量破片的初速与末速,在速度衰减的整个过程中,划分出如表1的速度区间,可得在某一区间的飞行距离,所有区间飞行距离相加得到此破片整个飞行距离,从而绘制不同质量级别破片与飞行距离的关系曲线。结合破碎性试验威力数据,绘制破片累积个数与飞行距离的关系曲线,用Origin软件拟合得到累积破片数与飞行距离关系函数。

表1 速度区间Table 1 Velocity interval Ma

2 威力数据的关系

2.1 静态飞散角对应曲面面积

静态飞散角对应曲面面积定义为:以质心为球面球心,以对应半径为球面半径,用包含有效破片90%的两直线以弹轴为轴线旋转一周,将球面切割为两个圆形曲面和一个环带状曲面三个部分,其中环带状曲面为两直线所夹静态飞散角对应曲面,如图1所示。

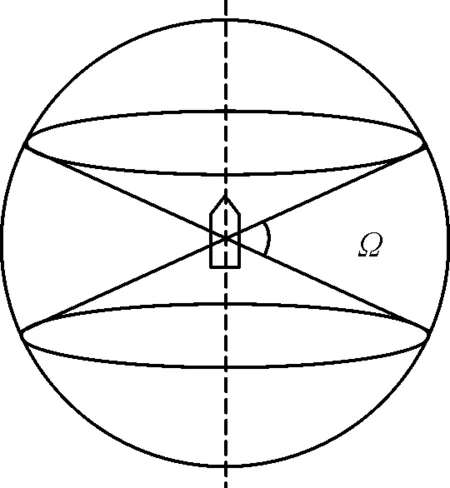
图1 静态飞散角对应曲面面积示意图Fig.1 Diagram of a surface with static scattering angles

其对应面积和投影距离公式为:

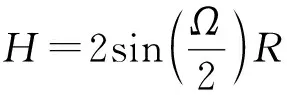
(7)

式中:SR为静态飞散角对应曲面面积;R为球面半径;H为环带状曲面在弹轴上的投影距离;Ω为静态飞散角度。

2.2 击穿杀伤半径

采用扇形靶试验方法,通过统计破片击穿靶板的结果,来计算击穿杀伤半径RC。扇形靶用木材为干燥的三等松木板,厚度为25 mm±1 mm,布靶圆心角为30°或60°,即每块扇形靶的扇面弧长,等于各扇形靶板所处圆周的1/6或1/12弧长,靶高为3 m。

2.3 威力数据之间的关系

击穿破片数与对应杀伤面积之比为击穿破片杀伤密度ρm,即击穿破片数与静态飞散角对应曲面面积存在如式(8)关系:

ρm=0.9Cm/SR

(8)

式中:ρm为杀伤密度;Cm为破片累积数;SR为静态飞散角对应曲面面积。

根据击穿破片杀伤半径定义可知,当击穿杀伤密度ρm=1/(1.5×0.5)时,其对应的半径为击穿破片杀伤半径RC。将试验值击穿破片杀伤半径代入,可得静态飞散角理论数据值。

3 静态飞散角的理论计算

3.1 拟合累积破片数与飞行距离关系

对杀爆弹开展破碎性试验并回收破片称重,按照相关标准统计出每一质量范围内的破片数,区间破片质量取破片区间中数(如破片质量区间0.1～0.2 g,区间中数取0.15 g),处理数据后绘制破片质量分布曲线如图2所示;破片累积个数与破片质量关系曲线如图3所示。

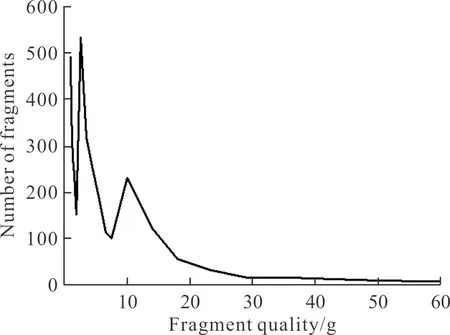
图2 破片质量分布曲线Fig.2 Fragment mass distribution curve

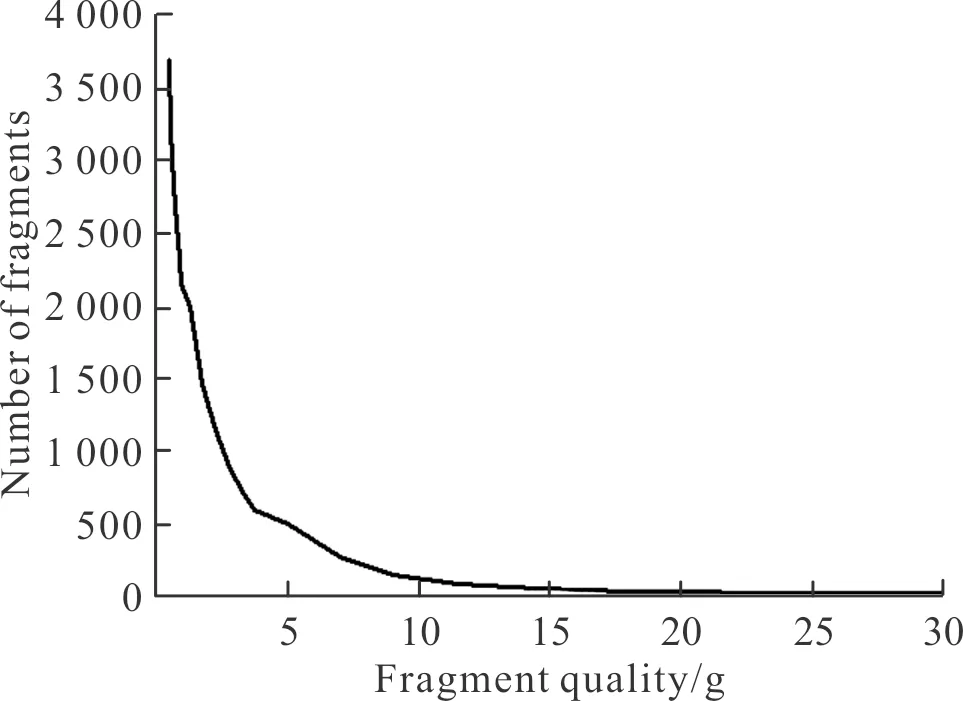
图3 破片累积个数与破片质量关系曲线Fig.3 Relationship between the cumulative number of fragments and the mass of fragments

杀爆弹参数如表2所示。

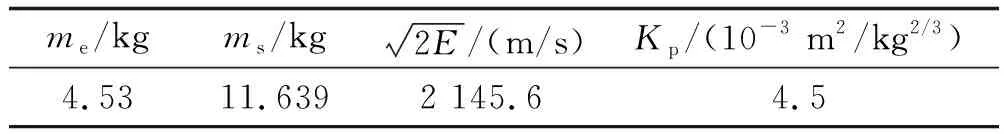
表2 杀爆弹参数Table 2 Parameters of the kill blasting projectile

文中动能E取98 J,空气密度取1.29 kg/m3,根据式(1)～式(6)可绘制杀伤距离Ri与的破片质量mi关系曲线如图4所示;破片累积个数Cm与飞行距离Rm的关系曲线及拟合曲线如图5所示。

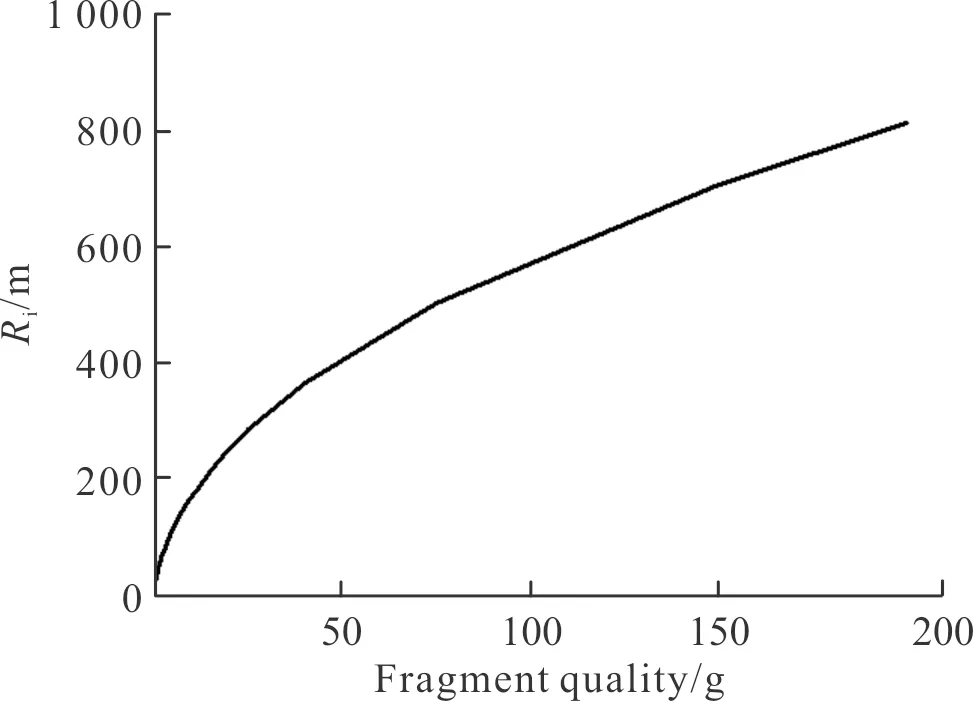
图4 杀伤距离与破片质量关系曲线Fig.4 The relationship between killing distance and fragment mass

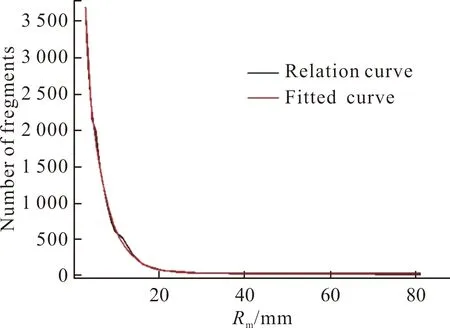
图5 破片累积个数与飞行距离的关系曲线及拟合曲线Fig.5 The relationship curve and fitting curve between cumulative number of fragments and flight distance

破片累积个数Cm与飞行距离Rm拟合方程Cm(R)为:

Cm=11.6146+5855.05862×e(-R/43.08306)+
91106.56655×e(-R/4.76063)

(9)

其相关系数r=0.99861。

3.2 静态飞散角理论威力数据值

将击穿破片杀伤半径试验威力数据RC=34.1 m,代入式(9)中得Cm=2742.4。将RC、Cm代入式(7)、式(8)中,得到静态飞散角理论威力数据值Ω′=14.66°。

4 结论

使用同一批生产的弹丸开展静态飞散角试验,采用直线排列的钢靶板测量破片数量和空间分布。试验结果显示破片的空间分布广泛,距离爆心较远位置破片分布密度较小,经统计,在战斗部轴线平面内,以质心为顶点所作的包含有效破片90%的锥角Ω=15°,对比数据分析可得:

2)若破片形状系数Kp取5.0(不规则),则同一质量等级破片飞行距离减少13.1%～38.7%,且破片质量越大,影响越大。因此在破碎性试验回收破片并按质量分组环节,可以将破片,按照球形、方形、柱形、菱形、长条形及不规则形状分类统计,按照不同形状所占比例确定破片形状系数Kp的取值,则理论计算更贴近试验。

3)基于部分威力试验数据的飞散角计算方法,计算得飞散角理论值,与试验结果一致性较好。