助推-滑翔导弹分段总体参数优化方法研究

罗 炜，雷 刚，郑晓龙

(火箭军工程大学，陕西 西安 710025)

0 引言

助推-滑翔式导弹是一类首先利用助推火箭将其发射至一定高度并实现分离,随后凭借自身气动升力在20～100 km范围内的临近空间进行高超声速飞行的武器。相较于传统导弹,助推-滑翔式导弹具有作战空域大、机动性能好、命中精度高等特点,逐渐成为世界军事强国的重点研制武器。

导弹总体参数优化是导弹设计优化的基础,针对导弹总体设计中关键因素-起飞质量,文献[1]推导出不同类型导弹起飞质量与航程、燃料比冲和载荷之间的解析关系,能够快速获得初始导弹起飞质量,但精度不高,仅可作为后续优化的初值。进一步,文献[2]在构建导弹起飞质量优化模型的基础上,采用3种优化算法进行仿真,为不同类型导弹的起飞质量和气动参数优化提供了有效的模型和算法。文献[3]对助推-滑翔式飞行器总体参数设计方法进行了初步探索,通过分析滑翔起点与关机点参数关系,重点研究了平衡滑翔条件下射程与导弹参数间的关系,为助推-滑翔式导弹总体参数设计提供了思路,但该研究采用大量拟合简化处理,在复杂弹道模型下的适用性不强。文献[4-7]利用各类改进型启发式算法对该多参数优化问题进行求解,一定程度上简化了求解难度,但存在收敛速度慢且易陷入局部最优的情况;文献[8]利用神经网络代替弹道解算过程,一定程度上提升了总体过程的优化速度,但是难以求解导弹飞行过程中的各项约束,使得弹道结果可信度下降。

为实现助推-滑翔式导弹直接起滑式飞行,针对具体飞行阶段,对分阶段优化思想进行改良并运用。首先,构建参数优化模型,并对优化参数关系进行分析;其次,采用分段方式完成解算流程优化及参数解耦;最后用自适应遗传算法进行寻优,求取最佳导弹总体参数。

1 总体参数优化模型

典型滑翔弹道可以分为助推段、无动力下压段、拉起段、滑翔段以及俯冲下压段。其中无动力下压段与拉起段的目的是使得滑翔弹满足滑翔起点条件,从而顺利进行滑翔段飞行,但由于这两段的飞行轨迹难以优化,通常采用数值拟合的方法进行逼近[9],这对整个优化设计而言是不利的。因此分析滑翔起点要求后,可选择采用直接起滑模式进行总体参数设计。

1.1 助推段模型

通过构建助推段模型,设计导弹起飞质量M、飞行程序角Φcx的变化方程,使其头体分离时刻tk满足起始滑翔飞行要求,并且以最小能量Emin达到要求射程。

1.1.1 导弹质量模型[8]

M=MT+MK+MF

(1)

MF=Mf+Mr

(2)

式中:MT为导弹弹头质量;MK为控制舱质量;MF为发动机质量,可分为机械结构质量Mf与推进剂质量Mr,通常取Mr=0.84MF。

1.1.2 飞行程序角模型

为简化后续飞行程序角优化难度,将飞行程序设为弹体坐标系与发射坐标系之间的关系(即俯仰角变化率)。整个助推段飞行过程包括垂直起飞段、第一次程序转弯段、跨音速段、第二次程序转弯段以及定程序飞行段。当前只在程序转弯段对飞行程序角进行优化控制,其余阶段按照固定模式调整控制。

1)第一次程序转弯

Φcx=α1(t)+θ

(3)

α1(t)=-4αmax1ea1(t1-t)(1-ea1(t1-t))

(4)

式中:αmax1为最大攻角的绝对值(主要考虑最大法向过载和姿态控制系统能力);a1为可调整的常数,控制转弯快慢;θ为弹道倾角(根据当前飞行速度计算);t1为导弹垂直起飞时间。

2)第二次程序转弯

Φcx=α2(t)+θ

(5)

α2(t)=-4αmax2ea2(t2-t)(1-ea2(t2-t))

(6)

式中:αmax2为最大攻角的绝对值(主要考虑最大法向过载和姿态控制系统能力);a2为可调整的常数,用来控制转弯快慢;t2为发动机关机时间。

1.2 滑翔段模型

滑翔段除不受发动机推力影响之外,其余因素与助推段相似,因此简要分析如下:

1.2.1 攻角模型[9]

(7)

式中:V1,V2,α1,α2为攻角控制参数,可以通过调整其值改变滑翔飞行弹道。

1.2.2 运动模型[12]

(8)

式中:V,θ,r,L分别为飞行器速度、速度倾角、地心距、射程,g和Re分别为重力加速度和地球半径。

2 基于自适应遗传的分段优化方法

2.1 优化参数关系分析

2.1.1 导弹总体参数与滑翔起点参数关系

在导弹总体参数设计中,为使得总体消耗能量最小,主要考虑弹体质量与飞行程序设计。根据1.1节可知,涉及到的参数有:MF,αmax1,αmax2,a1,a2。

以CAV-H为例,利用构建的助推段飞行模型得到导弹总体参数与滑翔起点部分参数关系如表1所示。

表1 导弹总体参数与滑翔起点参数关系表Table 1 Table of overall missile parameters in relation to glide starting point parameters

2.1.2 滑翔起点与飞行指标关系

利用1.2节构建的滑翔段飞行模型得到不同起滑条件下跳跃弹道参数关系如图2～4所示。

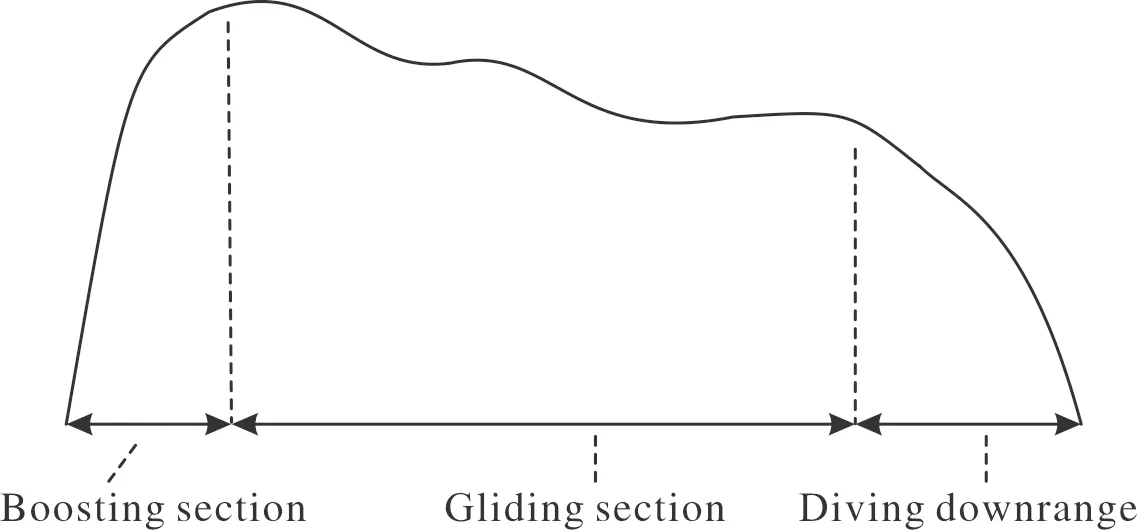
图1 直接起滑式滑翔弹弹道Fig.1 Direct launch glide trajectory

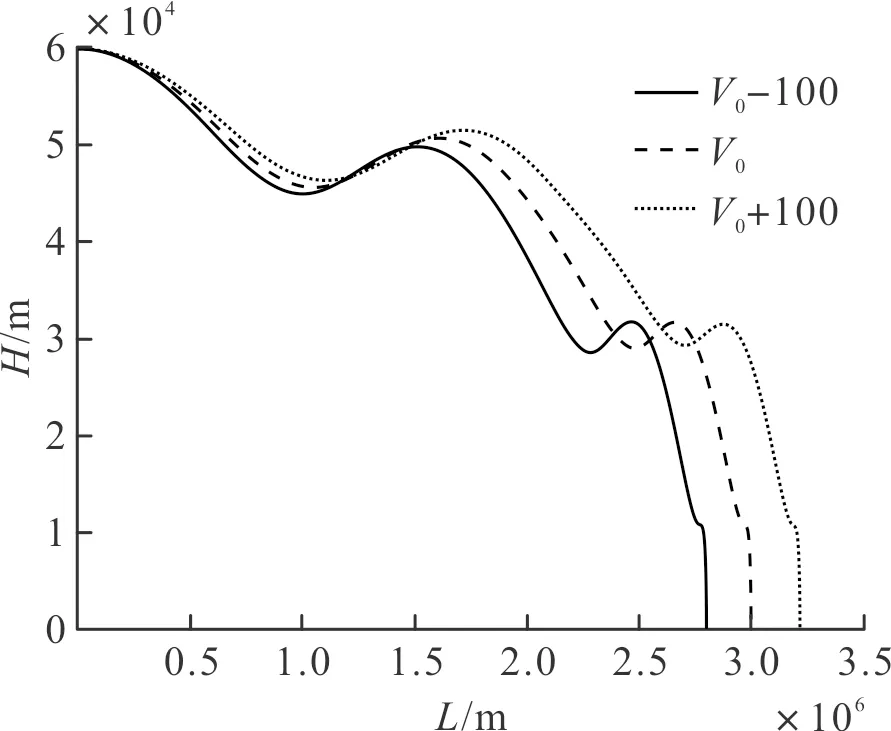
图2 射程随初始速度变化图Fig.2 Plot of range versus initial velocity

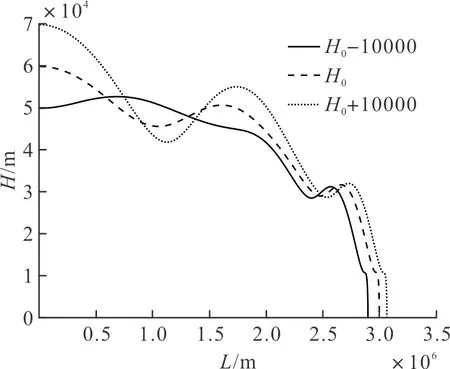
图3 射程随初始高度变化图Fig.3 Plot of range versus initial altitude

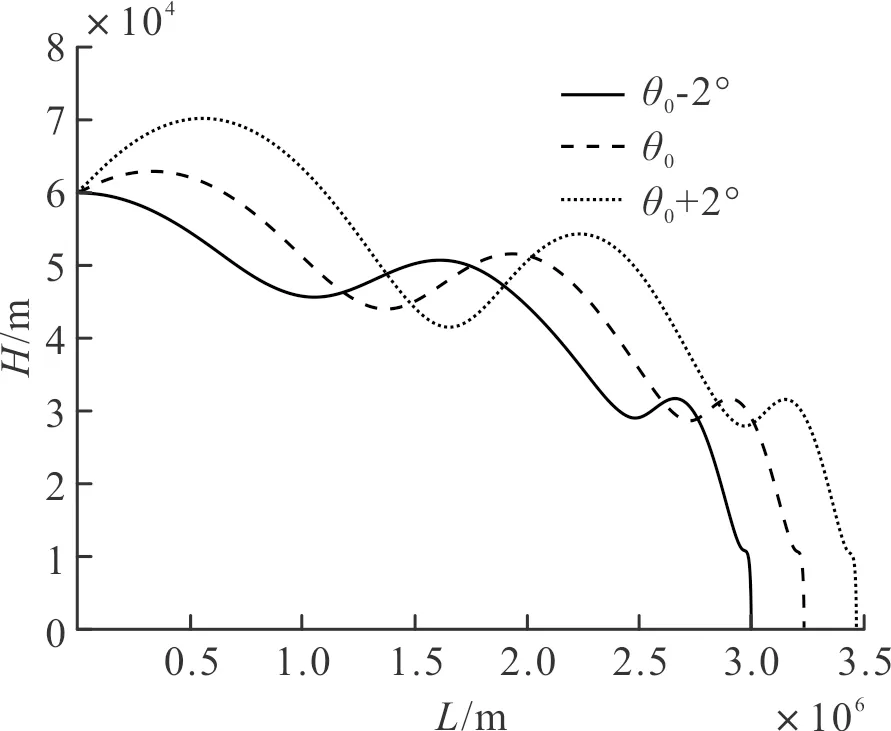
图4 射程随初始速度倾角变化图Fig.4 Plot of range versus initial velocity inclination

分析不同滑翔初始条件下的导弹飞行指标,从图2～图4可以看出,其他参数保持不变时,当前参数的正向偏量都将使得弹道跳跃幅度加大,同时在一定范围内使得射程变远。

2.2 分段优化方法设计

如图5所示,以往总体设计方法通常以助推飞行过程中的参数MF,αmax1,αmax2,a1,a2作为优化量,求解获得满足飞行任务的导弹起飞质量以及射程,此时,滑翔起点飞行参数V,H,θ仅作为中间变量进行考虑。因此传统方法在优化过程中涉及大量的参数耦合现象,降低了优化效率。

图5 参数优化过程图Fig.5 Parameter optimization process diagram

为消除参数耦合带来的不良影响,采用以下方法将中间变量纳入待优化变量中,并完成参数解耦。首先,在前文模型构建以及优化参数分析的基础上,将待优化飞行过程划分为助推段、无动力下压段两个独立的阶段;其次,在各个阶段分别对优化参数进行寻优,在助推段中,通过MF、αmax1,αmax2,a1,a2进行优化,得到期望的滑翔起点飞行参数V,H,θ,在无动力下压段中,通过对V,H,θ进行优化,得到期望的导弹飞行参数L,M。

在具体参数优化过程中,往往给定最终的优化目标,例如要求在确保导弹为最小起飞质量下达到一定的射程。从而可以根据期望目标,利用逆推的思想先进行阶段二的滑翔段参数优化设计,再根据结果进行阶段一的助推段参数优化设计。

尽管在整个过程中优化量由5个增加为了8个,但由于已经进行阶段划分,使得参数解耦,因此总的计算量有所降低,确保了方法的事件效率。同时在遗传算法中,采用相同的迭代数目,可以使得参数的搜索范围更广,因此提升了结果的适应度。

2.3 优化步骤

基于在最小起飞质量的条件下满足规定射程的最终设计目标,分两阶段完成导弹总体参数优化。

2.3.1 滑翔起点参数优化

综合考虑初始速度Vk、高度Hk、速度倾角θk,可以将其转化为导弹具有的能量,即:

(9)

要使滑翔起点处导弹初始速度、高度、速度倾角达到最优,即在通过数值积分求解弹道方程满足射程要求的情况下使得能量达到最小。因此,此阶段的目标函数为:

(10)

约束条件:

(11)

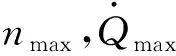
2.3.2 助推段参数优化

在第一阶段得出滑翔起点最优初始速度Vk,best、最优高度Hk,best、最优速度倾角θk,best之后,基于直接滑翔模式,通过设计导弹起飞质量M、飞行程序角Φcx变化规律,使得在满足各项约束条件的基础上主动段终点参数与滑翔起点最优参数相一致,从而使得整体过程达到最优。

在此阶段中,目标函数:

MF=MFmin

(12)

约束条件:

(13)

式中MFmin为最小发动机质量。

3 算例仿真

假设有效载荷质量MT为800 kg,导弹气动外形参考CAV-H飞行器,最大射程达到1 000 km,仿真结果如下。

3.1 滑翔段参数优化结果

在种群数量设置为200,迭代次数设置为100的情况下,优化仿真过程及结果如图6～图11所示。

图6 适应度变化曲线Fig.6 Adaptation change curve

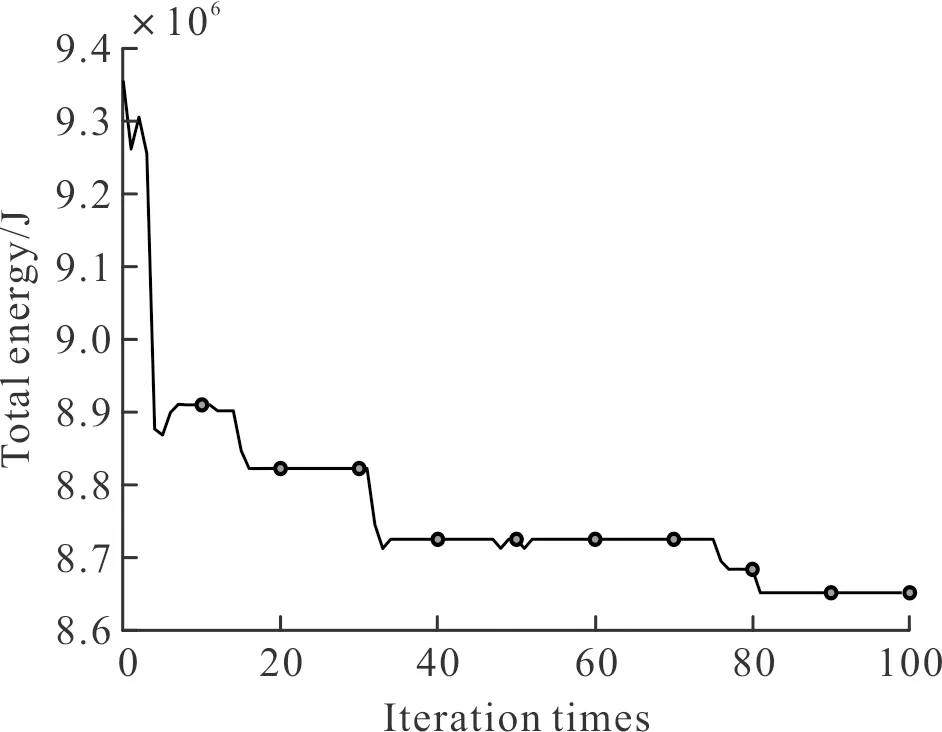
图7 能量变化曲线Fig.7 Energy change curve

图8 速度变化曲线Fig.8 Velocity change curve

图9 高度变化曲线Fig.9 Height change curve

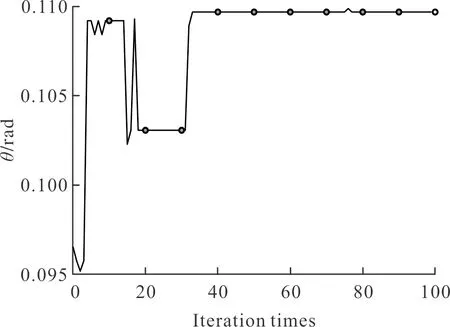
图10 速度倾角变化曲线Fig.10 Velocity Inclination Change Curve

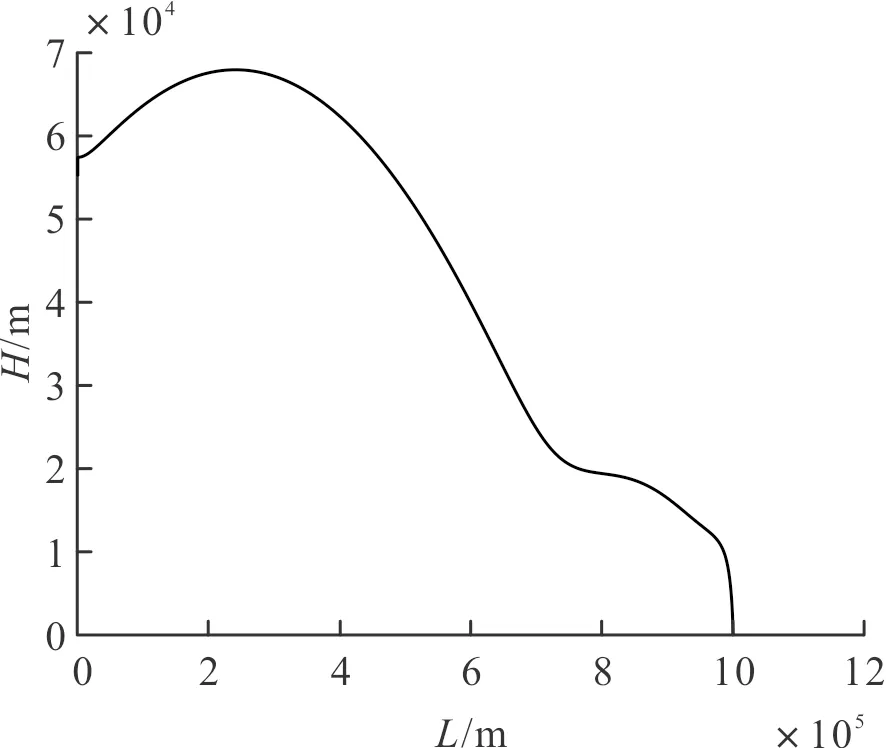
图11 最优条件下滑翔段弹道示意图Fig.11 Schematic of the trajectory of the glide section under optimal conditions

其中图6、图7分别表示适应度、飞行器剩余能量随迭代次数的变化,曲线表明在迭代次数为82之后算法已经具备良好的收敛性,此时剩余能量达到稳定。

图8～图10分别表示阶段一的优化结果V,H,θ变化关系。可以看出,优化结果最终都收敛于一定的数值,其具体大小如表2所示。

表2 最优初始参数结果Table 2 Optimal initial parameter results

此时的弹道为:

3.2 导弹总体参数优化结果

在2.3.1节的基础上运用文中提出的参数优化方法,得到最终的导弹总体参数优化结果如表3所示。

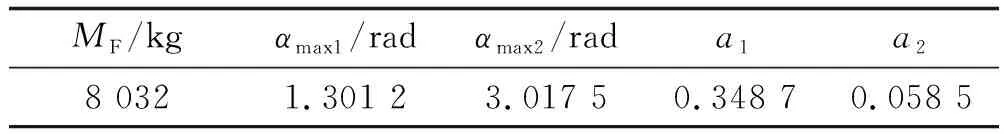
表3 导弹总体参数优化结果Table 3 Missile overall parameter optimization results

此时助推段过载变化曲线如图12所示,整个助推段承受的最大过载在4 g以内,可以确保飞行过程的稳定性。其中,第26 s由于飞行器处于跨音速飞行段,导致气动力变化剧烈,过载陡然增大。此后,由于进入超音速飞行阶段、且飞行高度较高,使得气动力影响减小,但导弹此阶段需要完成弹体快速下压、使当地弹道倾角尽快接近0,因此过载不断上升。

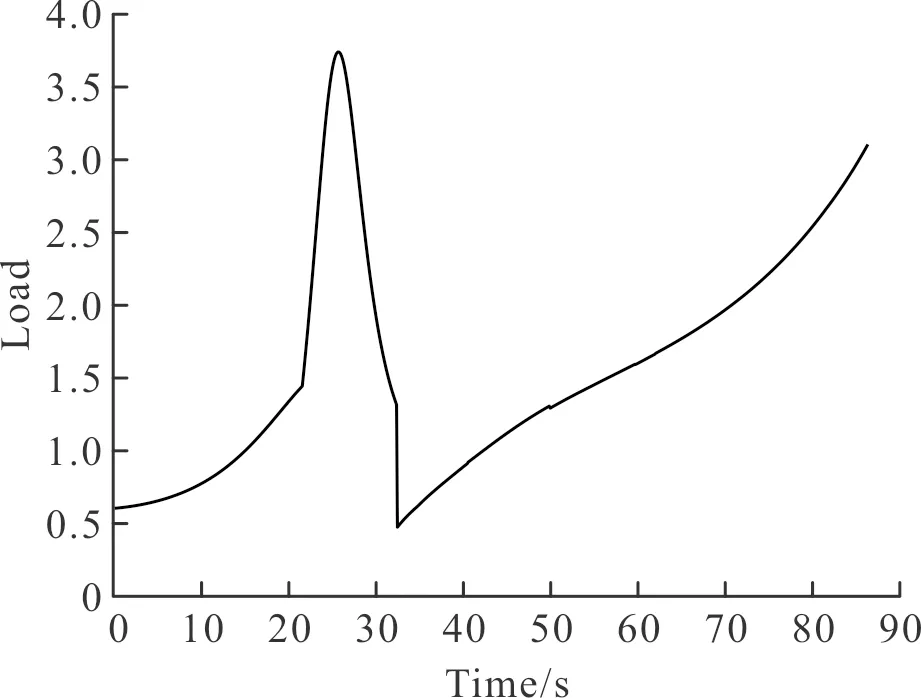
图12 最优条件下助推段过载变化图Fig.12 Plot of overload variation in the boost section under optimal conditions

3.3 对比分析

为了验证文中设计方法的优越性,在此加入传统设计方法(即不进行阶段划分而采用整体优化思路进行导弹参数设计)作为对比实验,并采用蒙特卡洛模拟,进行多次同等实验,得到最终结果的误差分布如图13～图15所示:

图13 蒙特卡洛模拟结果Fig.13 Monte Carlo simulation results

图13和图14均为蒙特卡洛模拟获得的最优起飞质量分布结果。图13中,实线、虚线分别表示采用文中优化方法以及采用传统方法得到的每次实验的最优质量结果,可以看出,文中方法所得结果散布较为集中。通过图14的箱线图可以更为直观的进行对比,左侧绿色箱线代表文中方法,其均值为8 030.4,极值分别为8 092.6,7 036.3;右侧粉色箱线代表传统方法,其均值为8 030.6,极值分别为8 153.4,7 009.8。对比可以发现文中方法优化得到的起飞质量散布更小,最大误差总体保持在0.7%以内。因此,可以认为文中优化方法精度更为可靠。

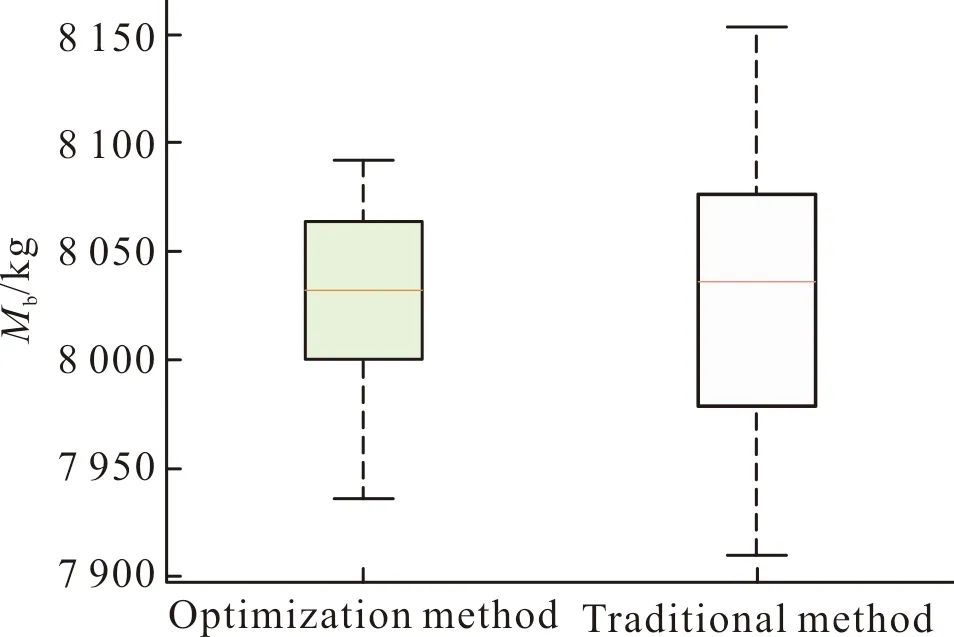
图14 最优质量分布箱线图Fig.14 Boxplot of optimal quality distribution

图15为蒙特卡洛模拟仿真时间分布,其中蓝色、橙色分别代表文中优化方法以及采用传统方法在不同时间区间上的仿真次数。可以看出采用文中方法,有70%的蒙特卡洛仿真时间小于4 s,且最长时间不超过5.5 s;而采用传统方法,仅44%的蒙特卡洛仿真时间小于4 s,且最长时间超过7 s。因此,可以认为文中优化方法的计算速度更快。

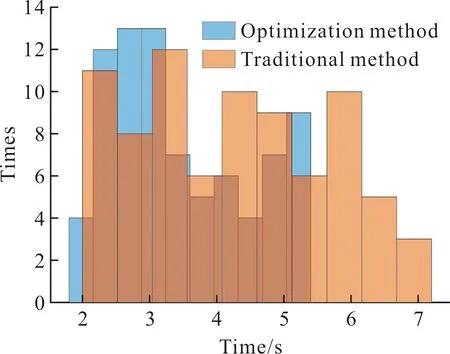
图15 仿真时长分布Fig.15 Simulation time distribution

4 结论

文中针对直接起滑式导弹总体设计问题,基于飞行参数耦合关系,对分段优化方法进行了改进,使得其能够更好满足导弹总体参数优化需求。与传统方法的蒙特卡洛仿真结果相比,文中方法能使参数优化结果的精确度提升7.63%,平均优化效率提升16.736%。由于该方法采用启发式算法进行参数优化,优化结果始终为次优解,只能无限逼近最优解,在参数的解析分析上存在一定的局限。下一步可以考虑在解析计算的基础上采用大模型网络不断拟合,以样本的多样性弥补优化结果无法达到全局最优的缺陷。