四自由度冗余驱动并联机器人的结构优化算法

李 袁，刘海平，王嘉恒

（1.郑州铁路职业技术学院，河南 郑州 450000；2.郑州大学机械与动力工程学院，河南 郑州 450001）

1 引言

并联机器人具有刚度高、操作方便等优点，在工业领域得到了广泛的应用。在并联机器人的优化设计中，提高并联机器人的刚度和灵巧度而受到越来越多的关注，优化算法对于消除冗余驱动并联机器人的奇异性具有重要意义［1］。

国内外研究学者对冗余并联机器人结构设计开展了大量研究，文献［2］对平面二自由度并联机器人（RAPM）的结构尺寸参数进行了优化，使得RAPM的平均刚度和工作空间达到了最大化。文献［3］对三平移并联机器人结构建立了动力学模型，在此基础上提出了多目标优化分析算法，通过搭建实验平台验证了所提方法的合理性。文献［4］针对某新型并联机器人的奇异位形和工作空间，在矢量代数法上推导了并联机器人雅可比矩阵以及约束方程，该研究工作可为并联机器人的机构优化设计提供参考依据。文献［5］利用针对某新型冗余驱动机器人进行了有限元分析，根据实际需求优化设计了冗余机器人的结构，通过实验验证了所设计的机器人具有较优的工作空间。文献［6］针对三自由度高刚性并联机器人进行了优化设计，在满足结构刚度性能的条件下，对该机构进行了逆运动学分析，通过仿真表明优化后的并联机器人具有较优的轨迹跟踪控制精度。文献［7］针对带约束条件下的并联机器人，提出了工作空间建模方法，在自主开发的实验平台验证了所提方法的有效性。文献［8］根据仿生学设计方法，建立了三自由度并联机器人的动力学模型，在此基础上分析利用Matalb软件仿真分析了优化结构的动力学特性，结果表明所优化的并联机器人具有较高的轨迹控制精度。在涉及平移和旋转自由度的空间RAPM的优化设计中，许多研究人员通常使用基于螺旋理论的运动/力传递指数［9～11］，这对于评价结构优化设计的合理性提供了重要方法。基于动力学的RAPM 性能指标已成功应用于平面RAPM［12］，但复杂空间RAPM的精确动力学模型将是一项艰巨的任务。本研究提出了一种基于广义雅可比矩阵的RAPM优化算法，用于优化设计混合平移和旋转自由度的RAPM结构尺寸。通过增加运动约束实现冗余驱动的方法，提出了一种通用的混合自由度RAPMs的维数齐次雅可比公式，推导了RAPM的维次齐次雅可比矩阵，在此基础上采用基于雅可比矩阵的优化算法对RAPM的尺寸进行优化。

2 基于RAPMs的连杆凸轮机构

本研究提出了一种基于连杆凸轮机构的RAPM，该RAPM是通过增加运动约束来减少EE的自由度来实现的。并联机械手的平台关节分布在三维空间中，球面关节不在同一平面上。如果在末端执行器（EE）的两侧引入两个点接触约束（两个凸轮机构），则末端执行器（EE）的两个自由度将受到约束，并联机构自由度为4。这种基于连杆-凸轮机构的RAPM是一种包含连杆和凸轮机构的空间并联机器人，具有六个驱动器，但有四个自由度。基于连杆凸轮机构的RAPM 三维模型，如图1所示。

Simonsen E等[8]通过研究认为，土体的弹性模量在经历一个完整的冻融循环后会降低20%～60%，而土颗粒的粗细程度会对冻融前后土弹性模量变化的幅度值产生一定的影响。土体强度的增大或者减小一方面常被认为是冻结过程土体密度的变化和冻融作用对土的结构性改变；另一方面跟土的状态和试验条件也有关,如果冻融导致土体含水量增大, 则土体强度就会降低，含水量不变时强度会增大。因此，在研究冻融循环引起土颗粒的强度变形等变化时，就不得不考虑含水率的影响。而在一些研究中也考虑了前期固结状态、冻结温度、冻融循环次数、围压等方面的影响作用。

这种RAPM设计类似人类的咀嚼系统，两个凸轮约束被用来模拟连接人类下颌骨髁突和颞骨的颞下颌关节，并沿着下颌窝作平移和旋转运动。凸轮机构的两种设计，点L和点R分别代表左右凸轮中心点，髁杆沿约束曲面运动，本研究采用第一种设计，控制髁杆以保持与约束面的接触，Fl和Fr分别代表左关节面和右关节面，如图2所示。

图2 凸轮机构的两种设计Fig.2 Two Designs of Cam Mechanism

对于传统的并联机器人，与机器人连接的关节始终是均匀分布且中心对称的。通常关节在同一个平面上。本研究的机器人主、被动机构分布具有不对称性，且与EE连接的关节不在一个平面内，球面关节分布在三维空间中，此外6个驱动机构的长度差异较大。该机器人的凸轮机构是一种被动点接触的高运动副，在凸轮机构的约束下，关节空间中的运动变得更加复杂。当给定EE点空间中所需的速度向量时，六个关节速度的差异性较大。

3 冗余驱动机器人的雅可比矩阵

末端执行器（EE）相对于全局参照系的位姿可由三个任意的非共线点来描述，由于EE点空间或关节空间中的变量是齐次的，因此基于EE点速度的雅可比矩阵在维度上是齐次的［13］，从而可以建立从笛卡儿空间到EE点空间的位置和速度映射。

综上所述，血清脂蛋白相关磷脂酶A2水平升高、血清D-二聚体水平升高、血清高密度脂蛋白水平降低、高血压病史是急性缺血性脑卒中的独立影响因素。脂蛋白相关磷脂酶A2、D-二聚体水平、高血压史与急性缺血性脑卒中呈明显正相关；高密度脂蛋白水平与急性缺血性脑卒中发生呈负相关。

通用RAPM一般具有平移和旋转自由度，基于EE点法可以建立齐次雅可比矩阵，如式（1）中虚线框所示。使用EE点广义速度代替EE点速度，笛卡儿速度也可以映射到EE点速度，如式（1）的后半部分所示。

式中：n—驱动关节的数量；j—RAPM 的广义坐标数；m—非冗余驱动PM对应的自由度数；Q—RAPM关节坐标的向量形式，包含n个参数；E—三个EE点坐标的向量形式，包括9个参数；GE—EE点的广义坐标，包含j个参数；X—非冗余驱动PM对应件笛卡尔空间中EE的坐标，由方向和位置组成，包括m个参数；GC—笛卡尔坐标系中RAPM的广义坐标，包括j个参数。

主要教学内容：通过参加工业工程专业的相关竞赛或完成校级、省级大学生创新项目，从而提升学生对所学知识和能力的深度和广度。教学地点：实验室和企业实习基地等；教学课时：3～12个月。

结合式（15）、式（19），得到：

4 基于连杆-凸轮机构的RAPM雅可比矩阵

4.1 位置分析

RAPM 的坐标，如图3 所示。RAPM 的所有球面关节Si（i=1，2，…，6）和万向节Ui（i=1，2，…，6）不在同一平面上，L点和R点分别表示左右凸轮中心点。移动坐标系M-XMYMZM（ΣM）固定在左右凸轮中心点连线的中点。固定坐标系固定在坐标系ΣM的起始位置，即当EE位于起始位置时，ΣM与重合。全局坐标系OB-XBYBZB（ΣB）位于坐标系的下方，坐标的原点和轴线方向。虽然EE相对于坐标系ΣBS的姿态可以用三个任意的非共线点来描述，本研究选用对称分布的点来简化计算，选取等腰三角形中点L（xL，yL，zL）、R（xR，yR，zR）和I（xI，yI，zI）作为三个EE点。

图3 RAPM的运动图Fig.3 Kinematic Diagram of the RAPM

式中：x—xLeft或xRight，z可以为zLeft或zRight。

由式（5）可得yL。同样LR和IR的长度是固定的，右凸轮与右曲面保持接触，可以计算出xR，yR，zR。平台节点Si相对于坐标系的坐标可由式（4）获得，为了计算关节坐标Q，即Qi的长度，可以在ΔBiSiUi中得到：

如图2（b）、图3所示，EE的左右两侧分别受到曲面Fl和Fr的约束，这两个曲面在XM-ZM平面可表示为zLeft=fLeft（xLeft）和zRight=fRight（xRight）。在本研究中，两条二次多项式曲线定义如下：

通过混合自由度消除了维度的不一致性，关节空间与EE点空间之间速度误差的放大因子可用雅可比矩阵来描述，雅可比矩阵影响速度传递的精度。EE点空间与关节空间的映射关系，如图4所示。图中的椭球表示关节空间或关节空间速度误差所组成的欧氏空间，在EE点空间中给定一个期望的速度向量，利用雅可比矩阵可以确定6个关节速度。对于机器人的某些构型，尽管在笛卡尔空间中的速度很小，但某些关节速度可能会非常大（如图4 中的），因此关节空间中的较大。在给定的工作空间内，在给定的工作空间内，可将最大或平均速度传输误差和传输误差的标准偏差视为精度指标。

由于EE两侧受两个凸轮约束，RAPM有四个自由度。理论上，任意四个广义变量都可以描述机器人的位形。在EE点空间中，点I的运动范围相对于点L和点R的运动范围较大，因此，参数xI，yI，zI，xL可以用来描述机器人的运动，记为GE。其余三个EE点的坐标yL、zL、xR、yR、zR可以根据几何约束计算出来。三个EE点坐标［xI，yI，zI，xL，yL，zL，xR，yR，zR］T定义为E，通过位置分析确定关节坐标Q，即该RAPM的广义坐标GE。

“嘘！”小达像正在全神贯注钓鱼的人忽然被人往水面上扔了一块石头一般，“小声点！眼看天就要黑了，说不定很快就能见到蜡像馆的‘幽灵’了！”

根据式（2），E必须首先由GE得到，zL可由式（3）的左凸轮接触点约束计算得到，考虑到LI的长度是固定的，则有：

可以看出RAPM 的驱动关节个数为6，广义坐标j的个数为4，对应的非冗余PM的自由度数为6。

两边平方得到：

其中，BiUi=Qie=Qi［0，0，1］T，e=［0，0，1］T，每个连杆的长度UiSi是常数，则有：

RAPM的关节坐标Q可由下式计算：

本文使用相关软件对上面提到的理论模型，即智力资本、战略柔性和创新能力3个因素之间的相互作用关系进行了分析，假设检验结果如表5所示。

4.2 基于EE点速度的雅可比矩阵

如上所述，每个连杆UiSi的长度是固定的，对式（8）进行微分：

式中：L—OBL的缩写，表示为点L相对于坐标系ΣB的坐标；同样，I—OBI的缩写；R—OBR的缩写。对式（11）进行微分：

其中，A是（6×9）矩阵，表示为：

其中,T表示切片时长,N表示切片后的快照数量,i为快照序号,i∈(1,N),x(i)表示第i张快照中节点的平均连接数,表示全部网络快照内的平均连接数,R(T)表示全部网络快照间的自相关性.R(T)的值反映了连续数据之间的自相关性,对于大多数自学习模型,输入数据间的相关性越低,数据特征的独立性就越高,模型的学习效果也就越佳.自相关函数曲线示意图如图2所示,理论上当R(T)第一次降为0时,数据的独立性最高,但相关研究表明,实际应用中通常取R(T)第一次下降到1/e(e为自然底数)时更为合适[15],这是本文选取最优时长T的依据.

式（13）可改写为：

相对于点L和点R，点I的运动范围更大，考虑到RAPM 的冗余约束，选择EE点空间参数xI，yI，zI来定义工作空间。应尽可能小，以达到较高的控制精度和各向同性。

现在的公司，更多的注重生产，产品的生产力成为一个企业发展的重要依据，因此，更多的企业对技术工人的重视程度越来越高，会计专业的难度，也造成了会计人才的稀缺，高工资高待遇往往出现在大型企业中，中小企业无力与其竞争，这些问题导致了很多企业的财务管理队伍不成熟，甚至人员都不健全，企业发展离不开财务管理，管理者一定要重视财务管理队伍建设，加大投入，只有将财务工作做好，公司才能合理的依据盈亏情况对今后的发展进行规划，当今社会，人才是最重要的，重视财务管理队伍建设，为公司今后的发展奠定良好的基础。

高占斌(1971—)，男，河北张家口人,副教授，硕士生导师，博士生，研究方向为内燃机性能、排放及增压技术。

该RAPM的广义逆雅可比矩阵写成：

5 优化算法

5.1 RAPM的速度传输

根据式（20）、式（21），有：

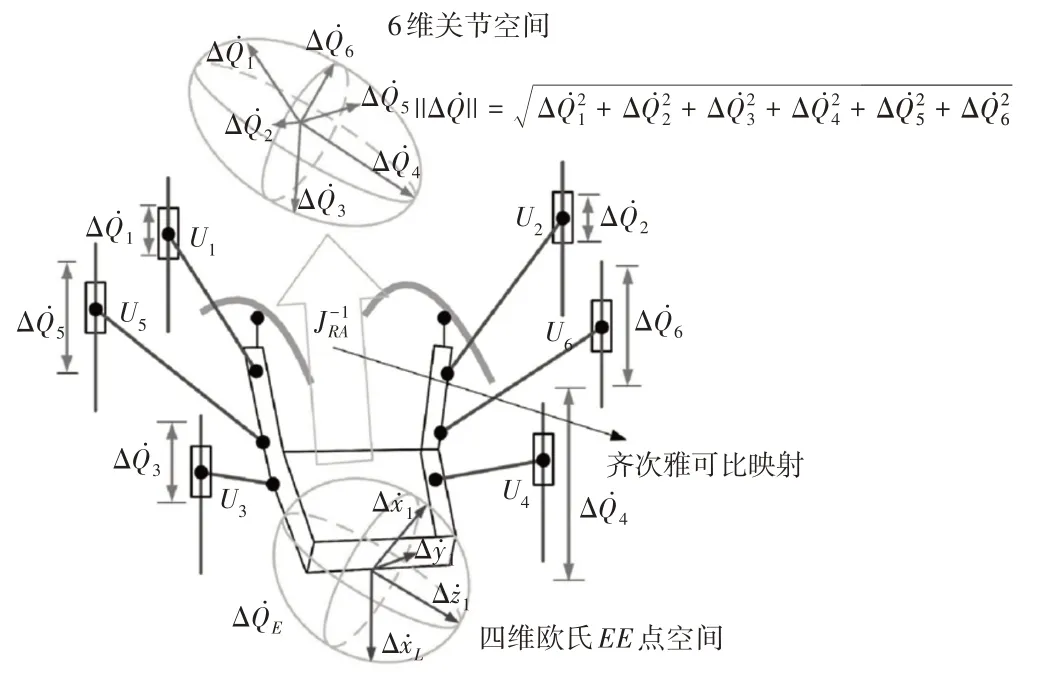
图4 关节空间与EE点空间的速度误差Fig.4 Velocity Errors Between Joint Space and EE Point Space

5.2 运动性能指标

假设任务空间中EE相对于某位形的速度误差在一个单位超球内，则与任务空间中单位速度扰动超球对应的联合速度误差可由式（23）计算。在实际任务中，当EE处于某一位置时，EE的速度可以指向所有可能的方向。为了评价该EE位置的速度传输性能，必须在EE空间中生成一组误差点。它们均匀分布在四维欧氏空间的超曲面上，代表不同方向的EE速度误差。另外，满足下面的式子：

当EE的速度矢量方向需要突然改变时，较小的有助于避免机器人关节速度发生较大的变化。为了让每个EE位形的速度误差向量在超球上的覆盖范围尽可能大，在四维欧氏空间的超曲面上指定5000组向量如图5所示，坐标满足式（24）。

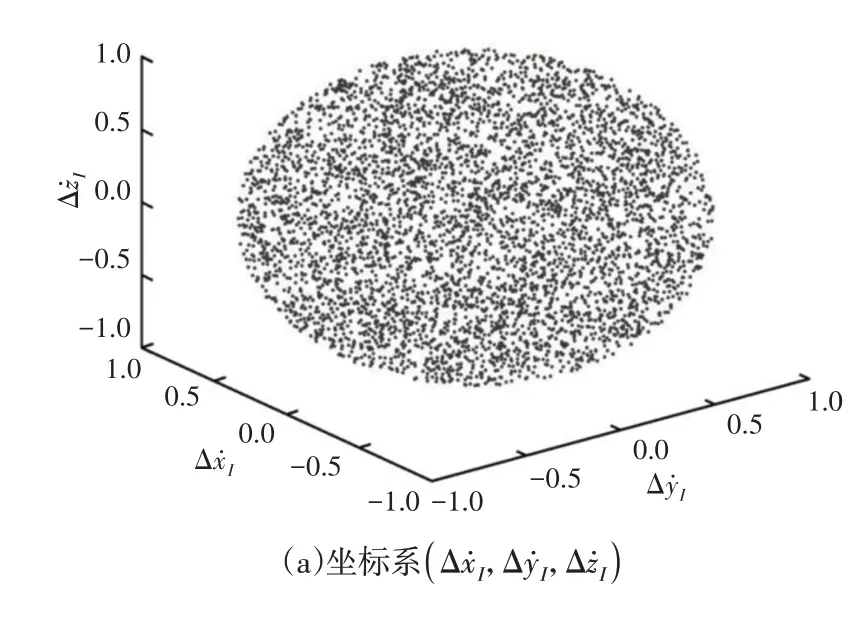
图5 三维坐标系下显示的5000组4D速度误差Fig.5 The 5000 Groups of 4D Velocity Errors Displayed in 3D Coordinate Systems

在优化过程中使用相同的速度误差向量，以保证算法的一致性。利用式（23），可以从EE空间的5000个速度误差得到关节空间的速度误差映射。对于给定的EE位形，可以通过最小化映射误差的平均误差和标准偏差来定义局部性能指标，计算局部性能指标的算法如下：

式（18）可改写为：

6 RAPM优化设计

6.1 利用优化连杆长度

本节对RAPM的6个驱动连杆UiSi（i=1，2，…，6）的长度进行优化，这是RAPM的重要结构参数。机器人结构在一定程度上符合生物结构，未考虑其他参数。通过最小化为给定的几个EE位形找到一组最佳的六连杆UiSi长度。优化设计模型为：

钟表品牌宝玑的创始人阿伯拉罕·路易·宝玑(Abraham-Louis Breguet)认识到了保护轴榫不受伤害的重要性，出现这种问题不仅会导致摆轮轴榫损坏影响走时精准度，更重要的是也会影响制表师的声誉。为了解决这一问题，钟表品牌宝玑的创始人阿伯拉罕·路易·宝玑做了一项发明，他用一个金属片固定红宝石轴榫，而不是直接将红宝石轴承固定在夹板上，这样就可以利用金属的弹性将手表受到撞击时的部分力量消耗掉，进而保证摆轮轴榫的安全。为了提高防震效果，这个金属片被做得尽量地曲折，因为越曲折就越长，越长防震效果越好。

连杆长度的几何约束为：

六个连杆的初始长度为l1=l2=143mm，l3=14=163mm，l5=l6=113mm。在优化过程中采用了遗传算法，求解最优解的帕累托边界，如图6所示。

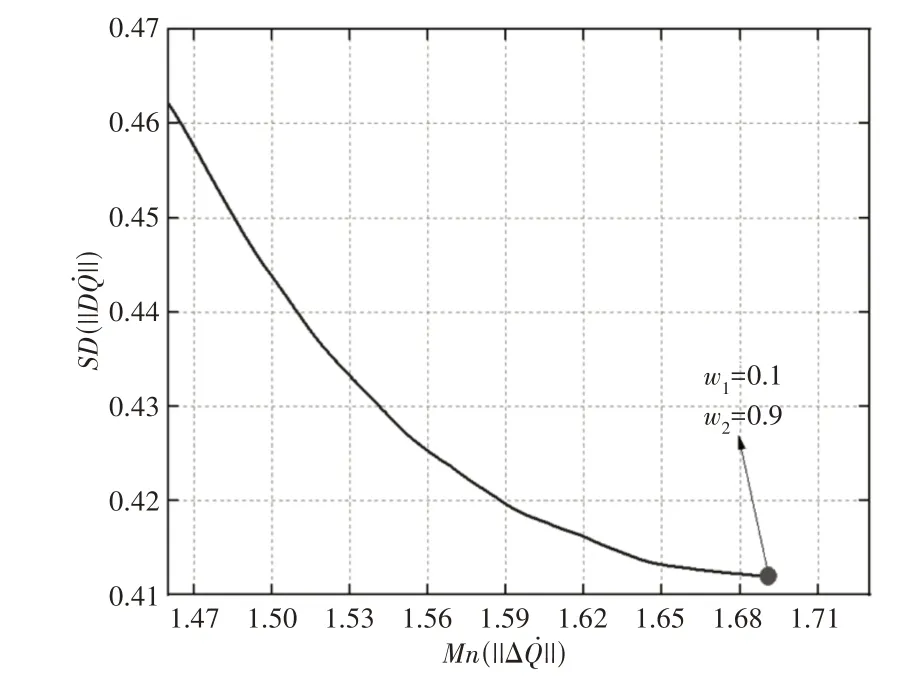
图6 初始点最优解的帕累托边界Fig.6 Pareto Frontier of the Optimal Solutions for Home Position

A:从描述来看，并没有什么好让你担心的。孩子喜欢和比自己大的人交朋友，这很正常。他的社会圈子还小，就只认识这位小姐姐，于是特别关注。你可以创造适当的机会让他们多接触，同时也让他有机会交同龄朋友，以平常心看待就是了。

表1 RAPM优化结果Tab.1 Optimization Results of RAPM

图7 RAPM的6个连杆初始布局Fig.7 Initial Layout of Six Linkages of RAPM

6.2 利用优化连杆长度

几何约束条件如式（31）所述，初始长度ll=l2=143mm，l3=l4=163mm，l5=l6=113mm。

图5为使用3种算法对4个不同形状不同规模的数据集进行聚类的准确率比较，可以明显看出改进后算法的聚类准确率保持在90%以上，聚类效果明显优于GP-CLIQUE算法和CLIQUE算法。这是因为使用本文方法对划分后的网格进行处理后，寻回了丢失的稠密区域，提高了聚类质量。而GPCLIQUE算法的准确率比CLIQUE算法略有提高，这是因为虽然GP-CLIQUE算法采用高斯随机采样的方法提升了聚类性能，但还是采用固定宽度划分方法，所以算法性能的提升低于本文算法。准确率计算公式为：Accuracy=ncorrect/n。

在计算工作空间时，将工作空间离散为节点是一种有效的方法。节点越多，结果越准确。但是，这种情况将大大增加计算机的工作负载。本节将每个EE坐标［xI，yI，zI，xL］上的两个节点之间的间隔设为1，根据优化目标的权重不同，可以得到不同的优化结果，不同w1和w2下的五组优化结果，如表2所示。其他参数，如图8所示。

表2 五组权重系数的优化结果Tab.2 Optimization Results of Five Groups of Weight Coefficients

表3 迭代优化过程中10组变量值Tab.3 Ten Groups of Variable Values During the Iterative Optimization

这五组结果都可以作为我们的可行选择，可以看出平均SD的值随权重系数w2的减小而增大，表明速度误差变得越来越分散，且波动较大。相反，在确定最终最优结果时，当权重系数w1增加时，平均的值明显减小。

7 结论

提出了一种新的冗余驱动方式，通过增加运动约束来减小机器人的自由度。推导了具有平移和旋转混合自由度的RAMP的通用齐次雅可比矩阵。以连杆-凸轮机构为例，提出了一种基于连杆凸轮机构的RAPM，并利用齐次雅可比矩阵推导出的新指标进行了尺寸设计。建立了末端执行器（EE）点空间与笛卡儿空间之间的位置和速度参数映射。通过算例表明，该优化算法对基于连杆凸轮机构的RAMP尺寸优化设计是有效的，适用于该类型RAMP的优化设计。