薄壁筒件内孔车加工变形自适应控制方法

黄荣学，黄 胜，邓喜飞

（桂林理工大学，广西 南宁 530001）

1 引言

薄壁筒件凭借结构紧凑、耐高温等优势广泛应用在航空等领域。但此类零件刚度较低，在制造和切削加工等过程中会导致变形，对后续壁厚精度控制造成不便，零件的质量无法得到保证。在零件制造业中，控制技术占据主要地位，是机械制造走向现代化的关键，也是一个国家发展程度的标志。控制技术不但可以提高制造能力，还会带来一定经济效益。因此，将该技术引入到薄壁筒件加工过程中具有重要研究价值。

文献［1］采用三点弯曲法向筒件内施加应力，记录轴向拉伸对应力和工件变形产生的影响规律；利用ABAQUS 软件构建数值模拟模型，通过生死单元法模拟工件变形情况，根据变形规律进行自适应补偿，达到变形控制目的。文献［2］分析弯曲变形理论，构建加工变形力学模型，采用有限元算法计算变形因子，分解力学模型；将加工标准作为控制限，依据应力的自平衡特征构建规范模型，通过任意变量的转化将工件参数控制在规范区间内。

但上述方法没有考虑车削加工过程中的振动因素，导致变形预测不够准确，进而影响控制效果。为此，这里将切削用量［3］和进给速度［4］作为车削加工的主要影响因素，建立变形误差模型，通过传感器技术采集切削力相关数据，采用模糊控制方法设计控制器自适应补偿变形误差，获取精准的控制量。

2 加工变形误差模型建立

2.1 切削车振动因素分析

薄壁筒件内孔的加工需要使用切削车，而车削振动是多种因素同时作用的过程，此种振动会引起加工参数错误，导致工件变形。这里分别从切削用量和进给速度两个方面分析切削车振动因素。

2.1.1 切削用量

如果切削过程在无振动的环境下进行，则切削力的变动会使切削车形成沿法线方向的振动［5］，此时切削用量的相关要素也会产生一定改变，利用下述公式表示该过程。

式中：ap(t)—瞬时切深；f(t)—进给量；v(t)—速度；ap0—名义切深；f0—名义进给量；v0—名义切削速度；h(t)—切削车沿法向量的振动位移；Kr—刀具主偏角；n—名义转速；d0—初始切削深度。通过切削力和切削用量二者之间的关系，获得瞬态变化的切削用量：

式中：F(t)—瞬态切削用量；CF—切削系数；l1，l2，l3—名义切深、进给量与切削速度的相应系数。

在无振动痕迹的表面切削时，因切削用量变化导致切削力产生的变化描述为ΔF(t)。如果切削表面发生振动，假设振动痕迹表示为αcos(ωt+b)，则切削用量变化导致切削力的改变可描述为：

2.1.2 进给速度

当切削过程非常稳定时，进给速度通常是一个常数，但在动态车削时，因振动因素影响，进给速度出现周期变化，导致切削力在切入与切出时发生相应改变。假设Cr表示进给速度影响系数，通过下述公式描述进给速度变化情况：

2.2 变形误差模型

上述振动因素会造成刀具偏置误差［6］，假设此种偏差为εT，因工件挠度造成的变形误差表示为εS，如果加工过程中，切削速度与进给速度始终不变，则变形总误差表示为：

式中：ρ—切削柔性系数；d—实际切削深度。

假设零件需要经过（m+1）次加工完成，则前m次的数据可以为第（m+1）次加工提供变形数据和补偿信息。通过干涉测量技术获取零件变形量。测量示意图，如图1所示。

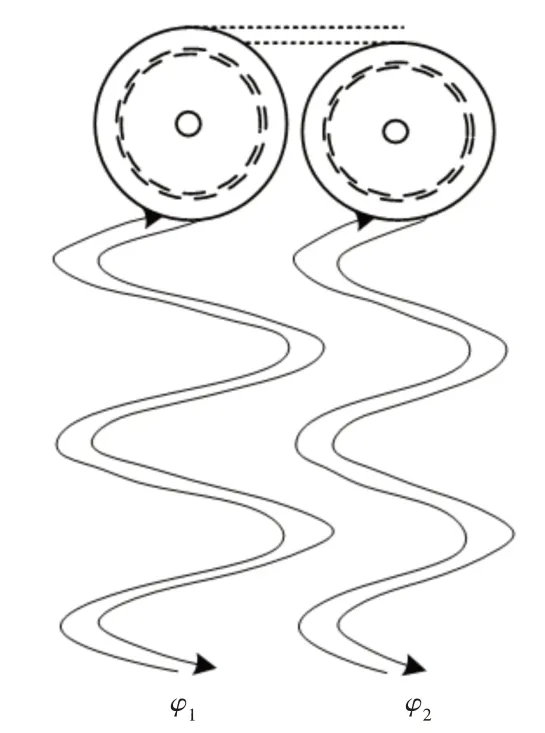
图1 干涉测量示意图Fig.1 Schematic Diagram of Interferometry

用φ1与φ2分别表示雷达所接收的零件第一次发射信号以及第二次发射信号的回波相位，由此得到两次回波信号间相位差为φ2-φ1。依据波长与相位对应关系明确不同零件加工过程中的变形量变化情况，可得待测量零件的变形量变化为s=λ(φ2-φ1)。其中，λ—发射信号波长。

考虑到干涉测量技术应用过程中受到噪声等因素的因素，为了保证测量的准确性，通过估计基线获取估计误差，对各测点进行时空滤波，获取不同候选点目标的非线性形变相位以及大气延迟相位。以此为基础修正干涉测量结果。

综合上述分析，在刀具轨迹平面内，确定参数化方向上的一点R1，因误差εT的影响，工件的理想加工面是刀具偏置后的平面。在切削柔性与切削力的同时影响下［7］，点R1的理论加工面厚度td1与真实厚度ti1存在一定差异，则该点加工误差εprocess1的计算公式如下：

建立上述加工变形误差模型，有利于分析变形机理，为自适应控制提供依据，便于误差补偿。

3 薄壁筒件内孔车加工变形自适应控制

3.1 基于传感器的切削力采集

切削车系统的工作过程复杂，控制对象和参数变量会实时发生改变。切削力作为主要控制参量，不仅和切削用量相关，还取决于工件材料、刀具等因素［8］。这里利用传感技术实时采集切削力的变化状况，并通过模糊控制算法实时控制切削力大小，使其满足工艺要求，减少变形情况发生。

3.1.1 传感器采集系统

切削力的采集方式分为直接和间接采集，其中前者通过传感器实现，传感器可进一步分为压电式与应变式。而间接测量则是观测电流、功率等物理特性来测量切削力，此种方式虽然能够节约成本，但受外界干扰较大，很可能造成控制失效，无法提高零件加工精度。

这里利用现阶段非常成熟的KISTLER压电传感器实现切削力测量，该设备具有结构坚固、分辨率高、防水、耐腐蚀等优势。

对于采集卡［9］的选择，利用PCI2006 采集卡，此卡具备较高的分辨率，采样频率高达100K/s，能够满足采集需要。利用采集卡提供的接口在开发软件下可完成数据处理等程序。

3.1.2 数据处理

加工过程中，因刀具和零件之间产生的相对运动，刀具会在三个方向产生作用力，分别为纵向、横向以及垂直分力，分别表示为Fx，Fy，Fz。通过对切削力的分析可知，切削力信号中包括其他频率成分，对测量结果产生一定干扰。

刀具在加工时，切削力的基频率表达式如下：

式中：Ns—主轴转动速度；

Z—刀具刀尺数量。

但实际信号中，不但有f基频成分，还存在转频率fn以及谐波。所以需使用低通滤波器处理切削力初始信号，去除高频干扰成分。为保证低通滤波器准确滤出无用信号，需要使采样频率fs高出信号最高频率fc两倍。数字滤波器具有精度高等优势，其种类较多，这里选用递归数字滤波器，不仅能够减少执行时间，还能扩大储存容量，满足实时性要求。

3.2 基于模糊理论的自适应控制

自适应控制是指在无人工直接控制环境下，通过控制设备确保被控目标的某物理量在规定范围内变化。在车削系统中将切削力作为主要控制量，结合传感器采集到的信息，根据变形误差模型，对切削力做实时调整。车削控制系统［10］的组成结构，如图2所示。

图2 车削控制系统组成结构示意图Fig.2 Structural Diagram of Turning Control System

由图2可知，切削力的控制是控制算法的核心部分，在算法设置过程中应满足如下需求：进给速度的改变应反映体现切削力的变化情况；算法过程简单，满足实时性需求；满足控制系统稳定运行要求。模糊控制以模糊语言变量与逻辑推理为基础，从控制器角度分析，此种控制手段属于智能控制范畴是现在智能控制领域的重要形式。

3.2.1 隶属度函数

隶属度表示模糊语言是某种模糊集合的程度，决定模糊推理效果。隶属函数必须体现目标的具体属性，每种模糊语言都有具体的定义，例如NB为负大、NM为负中、NS代表负小。任意一个语言值都与一个隶属函数相互对应。

3.2.2 论域、量化与比例因子

输入到控制器中的变量误差、变化率等内容称为论域，其中的所有值均为精确量，设置误差及其变化率的论域为[-xe，xe]、[-xec，xec]。

控制器控制量的论域表示被控目标实际需求的变量范围，设置为[-yu，yu]。该论域内的值同样为精确值，即：误差变量的模糊子集论域表示为：{-k'，-k'+1，…，0，…，k'}；控制变量的模糊子集论域描述为：{-g，-g+1，0，…，g-1，g}。

为了实现模糊化处理，需将输入变量变换到模糊集论域中，如果误差及其变化量因子分别表示为Ke和Kec，计算公式分别如下：

则输出控制比例因子Ku表示为：

则控制量从模糊集论域变换到基本论域的过程表示为：

式中：yu—控制量论域中某精确量。

模糊控制的基本过程，如图3所示。

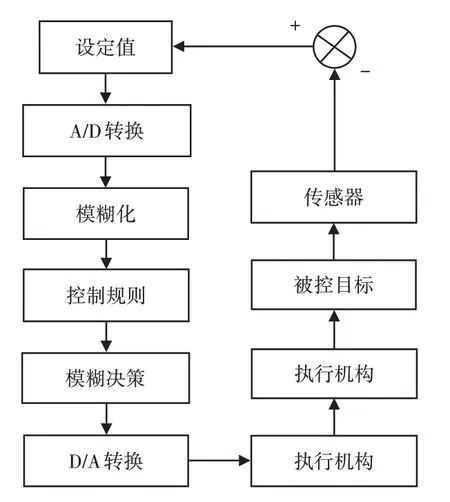
图3 模糊控制基本流程图Fig.3 Basic Flow Chart of Fuzzy Control

4 实验分析

4.1 实验准备

实验中，用于加工的薄壁筒件的长、宽和厚度为（1100×2400×2）mm，是从铝合金材质的厚板上切割下来的。首先需要将原材料在480℃的环境下保温3个小时左右，再对铝合金做拉伸处理，将拉伸量设置为3%，拉伸后的材料即可用于切割。切削车的相关参数如下：主轴转动速度为800r/min，机床探头型号选用RENISHAW探头，所有直线轴的定位误差在1μm之内，表明切削车的定位误差可忽略不计。

4.2 实验结果与分析

4.2.1 切削力与工件变形情况的实时测试

为证明所提方法的在线测量能力，在进给速度不同的情况下，利用所提的传感器测量方法分别获取加工过程中切削力与最大变形数值；另外在进给速度一定时，将切削力作为变量，测试工件最大变形值。测量时，均为每个进给速度或切削力当下数值加工后，利用干涉测量法得到的变形值。并将其与传感器获取的数值和理论值进行对比，测试结果，如图4～图6所示。由图4～图6可知，在三次测试过程中，通过传感器采集到的切削力和最大变形的趋势均和计算值相符，没有出现较大误差，误差低于0.3μm。表明该方法具备良好的采集功能，采集结果能够为自适应控制提供精准依据。另外，当进给速度逐渐上升时，切削力与变形情况大致呈现线性递增的趋势，而当切削力逐渐增大时，最大变形则呈现非线性增长态势。因此，该方法采集到的信息准确验证了进给速度、切削力和最大加工变形三者之间的模型关系，为进给速度的自适应调整提供参考。

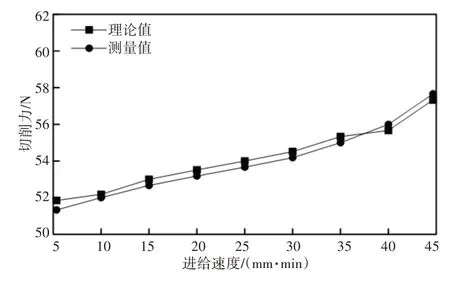
图4 进给速度不同时切削力测试情况Fig.4 Cutting Force Test at Different Feed Speeds

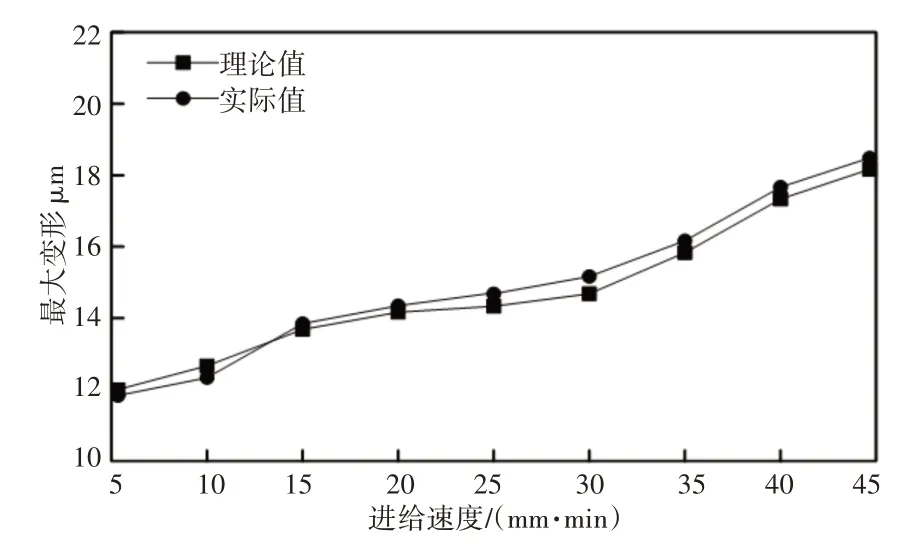
图5 进给速度不同时切削最大变形测试情况Fig.5 Maximum Cutting Deformation Test at Different Feed Speeds

图6 切削力不同时最大变形情况Fig.6 Maximum Deformation Under Different Cutting Forces

4.2.2 控制跟踪能力测试

根据切削车具体情况和工件参数特征，设定最优切削力和进给速度分别是120N和50mm/min，利用所提控制方法实时跟踪设定的加工参数，加工效果，如图7、图8所示。由图7、图8可知，未使用所提控制方法之前，对于切削力和切削速度的跟踪误差明显，幅值变化较高；但引入所提控制方法之后，跟踪结果能够始终保持在设定值左右，变动幅度很小，说明模糊控制器设置合理，通过传感器采集的实时信息，能够自适应调整控制参数，保证加工过程中产生的形变最小。此外，该方法不仅针对一个加工参数有效，可同时控制多个参数，证明了模糊控制算法的逻辑步骤满足了削切车的加工需求。

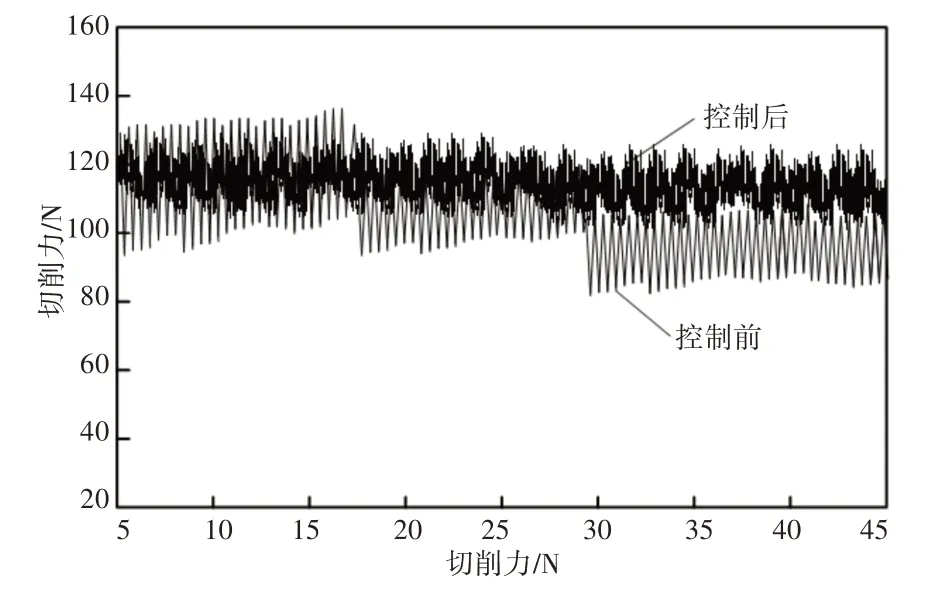
图7 切削力实时跟踪测试图Fig.7 Cutting Force Real-Time Tracking Test Diagram

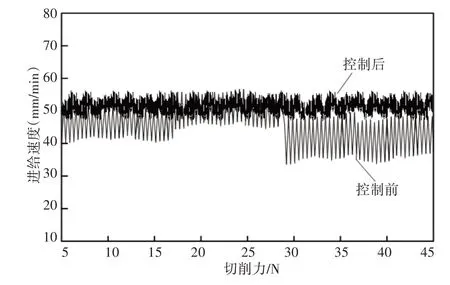
图8 进给速度实时跟踪测试示意图Fig.8 Schematic Diagram of Feed Speed Real-Time Tracking Test

5 结论

为减少薄壁筒件内孔加工的变形程度，提高工件质量，这里研究了薄壁筒件内孔车加工变形自适应控制方法。（1）研究过程中，这里将传感器技术与模糊控制理论相结合，通过传感器实时采集加工过程的相关信息，分析控制流程，设置模糊控制器，实现薄壁筒件内孔车加工变形自适应控制。（2）测试结果表明，所提方法能够精准测量加工参数变量，得到的跟踪控制结果与理想值相符，最高误差为0.3μm。（3）在今后研究中，应不断调节量化与比例因子，获取不同加工阶段的控制特点，提高复杂加工过程的控制效果，进一步提高工件质量。