PSOGA算法在望远镜实验基座控制系统中的应用

徐 蕾，王国民，王 海，徐 进

（1.中国科学院国家天文台南京天文光学技术研究所，江苏 南京 210042；2.中国科学院天文光学技术重点实验室（南京天文光学技术研究所），江苏 南京 210042；3.中国科学院大学天文与空间科学学院，北京 101408）

1 引言

为开展北半球可见天区的原初引力波观测，拟在西藏阿里地区建设原初引力波探测望远镜。引力波望远镜探测基座为方位-俯仰型结构，方位轴与地面垂直，俯仰轴与方位轴垂直，具有结构紧凑、承载能力强等优点。区别于普通光学探测望远镜，为满足观测要求，实现对可见天区的扫描，引力波探测望远镜需要方位轴的高速高精度扫描，最大扫描速度可达20°/s，精度要求不超过20″。因此，研究如何在高速情况下的保持高精度控制是其中的关键问题。

引力波探测望远镜基座的控制系统采用Delta Tau Turbo PMAC系列UMAC作为运动控制器，内部以PID控制与速度/加速度前馈调节器的组合作为控制器［1］，因此望远镜的控制精度与PID控制与前馈控制的参数选取密切相关。

传统的PID工业整定法［2］对非线性、时滞、时变系统难以达到控制要求，因此智能化的方法逐渐应用于参数整定中，主要有：基于继电反馈的参数整定方法、基于模式识别的参数整定方法等。基于继电反馈的方法鲁棒性强，但整定周期过长。基于模式识别的方法应用简单，不需要已知模型阶次等先验信息，但启发规则复杂。而且这些智能整定方法无法作用于特定的优化指标，如ISE，IAE，ITAE等，因此需要智能优化算法，如遗传算法［2］、粒子群算法［3］等。采用遗传算法（GA），可以获得较好的控制精度和抗干扰能力，但存在未成熟收敛和寻优效率低的问题。采用粒子群算法（PSO），可以获得较好的控制精度、稳定性和抗干扰能力，但易陷入局部极值。因此，一些学者将遗传算法与粒子群算法融合（PSOGA）［4］，以充分发挥两种算法的优点，克服二者的缺点。目前PSOGA算法应用于共阵天线模式优化、雷达调度、液体控制系统、机器人控制器等。

综上考虑，结合阿里原初引力波探测实验基座对方位轴高速高精度的控制要求，这里对GA算法、PSO算法及PSOGA算法的性能进行仿真对比，并将优化参数应用于实验电机，得到实际的控制结果。通过对比三种算法在不同速度下的调节时间与均方误差，验证了PSOGA算法的可行性。

2 控制器驱动电机模型

实验验证过程为：DELTA TAU公司的UMAC运动控制器通过Geo Direct PWM Drive驱动器控制Etel公司的TMB360力矩伺服电机，通过德国某公司的RON287码盘读取位置反馈。控制器控制电机根据程序增加命令位置，与位置传感器读取的实际位置比较，并计算输出。仿真中采用三环控制系统：电流环、速度环、位置环。

2.1 电机参数

实验中采用TMB360 电机作为驱动。为在SIMULINK 中建立系统的仿真模型，需根据实测数据，计算电机的转动惯量、阻尼系数、空载时的负载扭矩以及电机的粘滞系数等参数。根据电机的力矩平衡公式：

式中：T—输出力矩；T0—负载力矩；Ω—角速度；fc—粘滞摩擦力矩。使用UMAC驱动电机，在系统开环状态下，分别施加不同扭矩命令、速度命令，测量电机的电流、速度、加速度数据，并对数据进行最小二乘法拟合，获得相关参数如下：

固定负载扭矩T0=3.6696N·m

阻尼系数B=0.1502N·m（/rad/s）

转动惯量J=0.4688kg（/rad/s²）

粘滞系数fc=0.1263N·m（/rad/s）

2.2 电流环

UMAC中电流调节器结构为PI结构，其原理图，如图1所示。

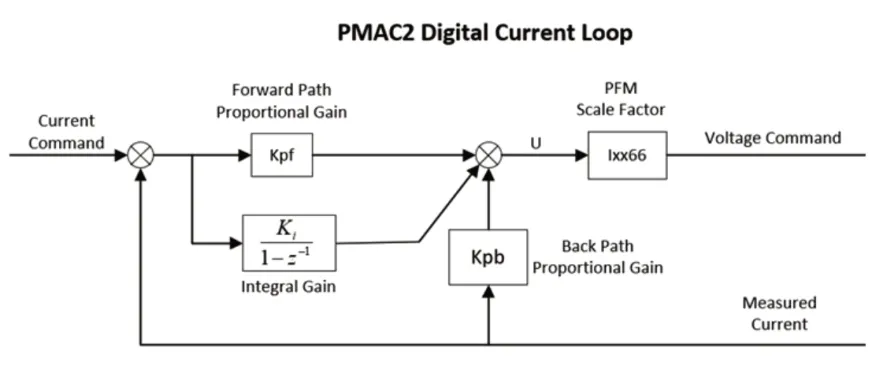
图1 UMAC中的电流调节器结构Fig.1 Current Regulator Structure in UMAC

图中：Kpf—前向比例增益；Ki—积分增益，其计算公式为：

式中：Isat—相电流A/D转换器最大电流，Isat=Vsat/Kc；Kc—电流传感器增益；Rpn—电机相间电阻；Vcmax—A/D转换器最大电压；ζ—期望阻尼比；Lpn—电机相间电感；VDC—放大器的直流电压；ωn—期望自然频率。

根据公式计算可得：电流调节器Kpf=0.672，Ki=0.036。

2.3 速度环与位置环

本实验控制系统的速度环与位置环结构包括前馈控制、PID控制等结构，结构由UMAC控制器给出，如图2所示。

图2 UMAC控制器结构Fig.2 Structure of UMAC Controller

图中：KP、Ki、Kd、Kvff、Kaff—实验待优化参数。

3 智能算法

分别采用GA算法、PSO算法以及PSOGA算法的优化控制器参数。

3.1 GA算法

遗传（GA）算法是由美国Michigan 大学的Holland 教授于1969年提出的模拟进化算法，可用来求解极值问题，具有较强的鲁棒性和通用优化能力，广泛应用于自动控制、计算科学、模式识别等领域。其算法流程图，如图3所示。

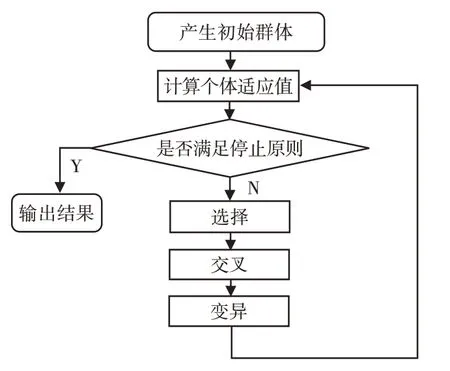
图3 GA算法流程图Fig.3 Flow Chart of GA Algorithm

在最优化过程中，用适应度函数来评估个体的优劣，其选取直接影响算法性能，实验中选取的适应度函数为绝对误差积分准则（IAE）基于这种准则设计的系统，具有适当的阻尼和良好的瞬态响应［5］。目前常用参数范围是种群规模为［20，200］，交叉概率为［0.5，1.0］，变异概率为［0，0.05］［6］。在本实验参数优化中，设定种群规模为100、种群区间为［0，1000000］、交叉概率为0.6、变异概率为0.05、迭代遗传次数为100，误差准则选取IAE，终止条件选取超过迭代次数或适应值小于0.1。

3.2 PSO算法

粒子群算法（PSO）是由Kennedy 和Eberhart 等于1995 年开发的模拟鸟群运动的随机优化技术。种群中的个体称作微粒，在D维空间中搜索潜在解，用位置、速度和适应度值作为粒子特征。微粒在搜索空间中不断改变状态，直到最优状态。PSO算法的流程图，如图4所示。

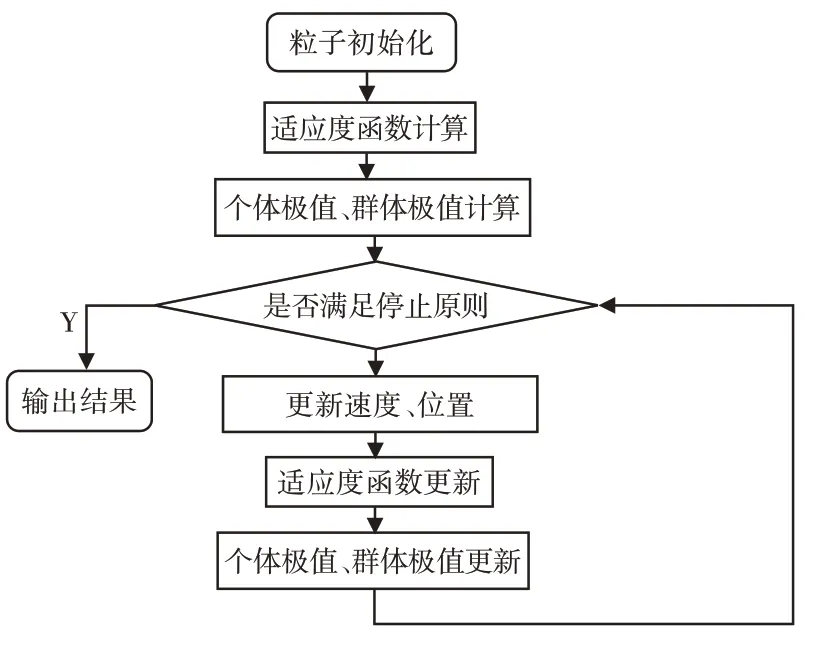
图4 PSO算法的流程图Fig.4 Flow Chart of PSO Algorithm

粒子通过个体极值和群体极值更新自身的速度和位置，更新公式为：

式中：V—速度；ω—惯性因子；c1、c2—系数；r1、r2—随机数；X—位置；Pid—个体极值Pbest；Pgd—群体极值Gbest。

通常令学习因子c1=c2=2，r1、r2为［0，1］随机数，惯性因子ω在［0.4，0.9］时，能较快定位最优解的大致位置［7］。在本次优化中，设定粒子群规模100、搜索区间［0，1000000］、惯性因子0.6、迭代次数100、c1=2、c2=2；误差准则选取IAE，终止条件选取超过迭代次数或适应值小于0.1。

3.3 PSOGA算法

GA 算法和PSO 算法在最优化处理中应用广泛，但遗传算法存在收敛慢、局部搜索能力差等现象，PSO 算法存在全局收敛性差、易陷入局部极值等问题，因此提出PSOGA 融合算法，既保证全局搜索能力，又有较快的收敛速度，且不易陷入局部最优，从而提高算法的性能。

PSO与GA算法的融合有多种方式，如并行式、串行式与嵌入式混合。并行式混合即两个算法并行运行，算法保持各自独立性，易于实现，但两种算法之间没有交流，缺点仍然存在。串行式混合将两种算法呈串行结构先后寻优，算法相对简单，可以改善收敛速度，但会增大时间复杂度。嵌入式混合是将其中一个算法思想嵌入另一个算法，既能充分发挥两种算法的优点，又能摒弃两者缺点［6］。

本次实验采用一种将GA 算法嵌入PSO 算法中的融合算法（PSOGA）［8］，基本思想为：在PSO 算法中，引入GA 算法的选择、交叉和变异操作，在每次迭代过程中选取适应度好的前一半粒子进入下一代，后一半粒子经过选择、交叉和变异操作产生子代，与父代作比较，适应度好的前一半粒子进入下一代。其算法流程图，如图5所示。

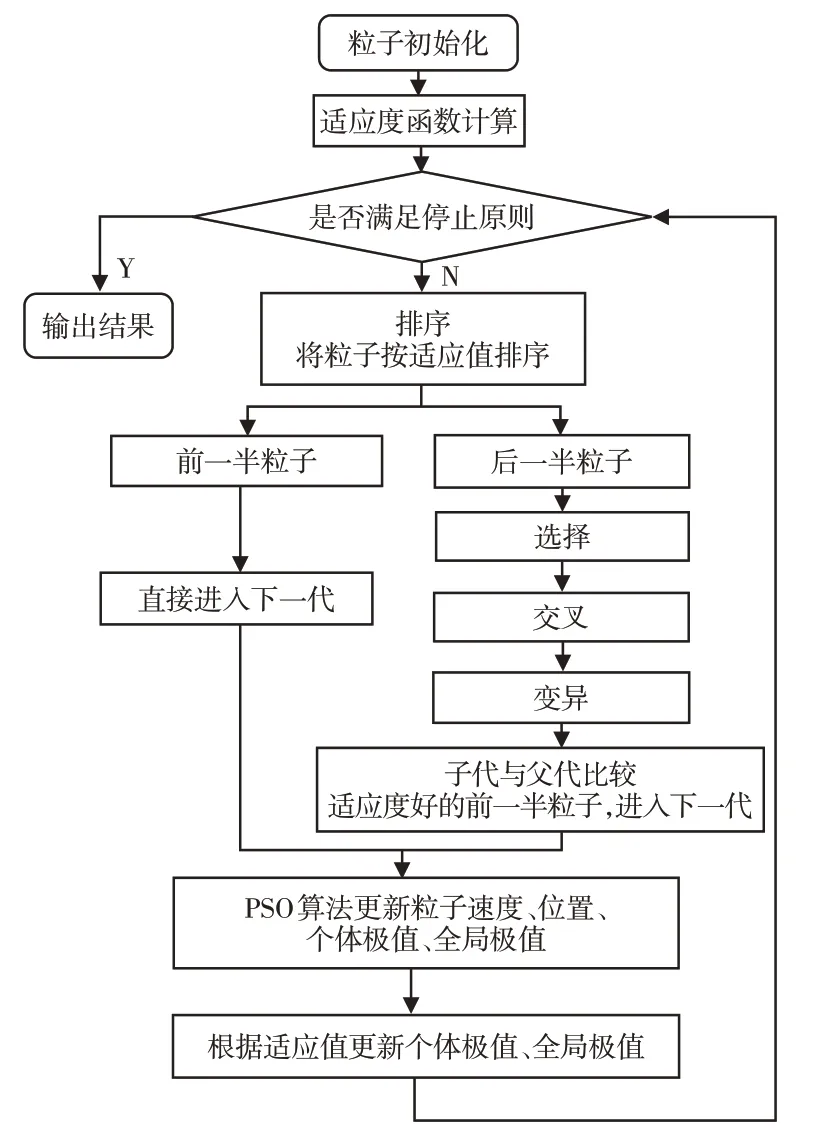
图5 PSOGA算法的流程图Fig.5 Flow Chart of PSOGA Algorithm

在本次参数实验中，为与GA、PSO算法对比，选取相同的参数，粒子群规模为100、搜索区间［0，1000000］、惯性因子0.6、迭代次数为100、c1=2、c2=2、交叉概率为0.6、变异概率为0.05、误差准则选取IAE，终止条件选取超过迭代次数或适应值小于0.1。

4 实验结果

4.1 三种算法优化结果

GA、PSO、PSOGA 三种算法优化UMAC 中控制器参数结果，如表1所示。

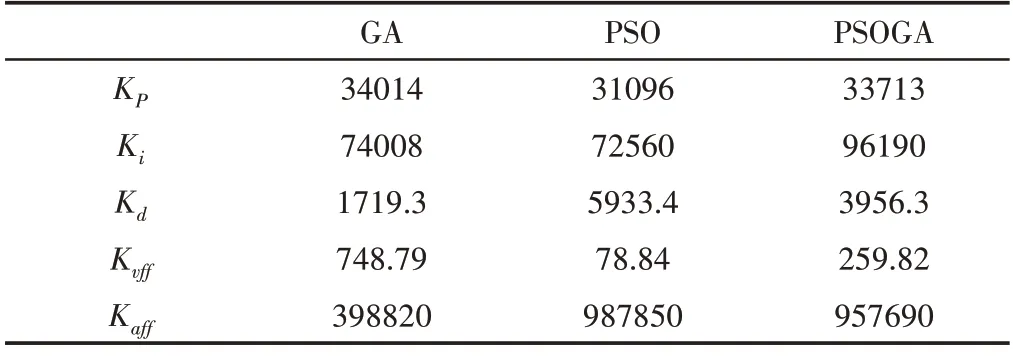
表1 三种算法优化结果Tab.1 The Results of Three Algorithm Optimization

4.2 三种算法参数的仿真阶跃响应曲线

GA、PSO、PSOGA三种算法参数在SIMULINK中的仿真阶跃曲线，如图6所示。三种算法的阶跃响应指标对比，如表2所示。其中，调节时间取误差稳定在稳态值的±2%的范围的最短时间。根据三种算法的阶跃响应曲线与指标数据可知，PSOGA算法调节时间较短，分别为PSO 算法的47.06%，为GA 算法的46.03%；且PSOGA 算法具有超调量小的特点。PSOGA 算法的参数在阶跃响应中具有较好的效果。

表2 三种算法阶跃响应指标Tab.2 Step Response Index of Three Algorithms

图6 三种算法的阶跃响应曲线Fig.6 Step Response Curves of the Three Algorithms

4.3 三种算法参数的仿真与实测跟踪曲线

由于方位轴的扫描速度为（5～20）°/s，实验中取最大速度20°/s测量三种算法的跟踪响应。仿真跟踪曲线，如图7所示。实际跟踪曲线，如图8所示。根据20°/s速度下的仿真和实际误差曲线可知：相比于PSO算法和GA算法，PSOGA算法具有更短的稳定时间和相对较小的误差。且在实际测试中，PSOGA 算法在5°/s、10°/s的速度下，也具有相同的优越性。

图7 20°/s时，三种算法的仿真跟踪误差曲线Fig.7 Tracking Error Curves of the Three Algorithms at Different Speeds

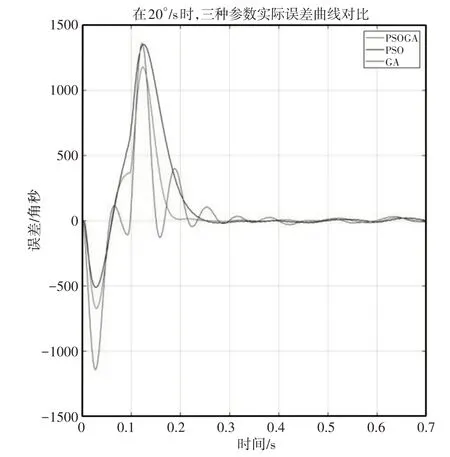
图8 20°/s时，三种算法的实际跟踪响应曲线Fig.8 Tracking Error Curves of the Three Algorithms at 20°/s

4.4 实际与仿真数据对比

三种算法在20°/s 时的仿真和实测误差指标，如表3 所示。其中，稳定时间取误差稳定在20″内的时间，均方根误差取稳定时间之后的误差均方根值。

表3 三种算法的跟踪响应指标Tab.3 Tracking Response Indicators of Three Algorithms

根据三种算法的误差指标可知：在20°/s 的仿真中：PSOGA算法的稳定时间为PSO算法的72.13%、GA算法的70.38%；误差均方根为PSO算法的68.21%、GA算法的66.64%。在20°/s 的实测中：PSOGA算法的稳定时间为PSO算法的78.70%、GA算法的43.34%；误差均方根为PSO 算法的77.15%、GA 算法的73.60%。因此，PSOGA算法在仿真和实际应用中都具有稳定时间短，均方根误差小的特点，具有更好的控制效果。

5 结论

实验证明，不论是在仿真还是实测中，对比于GA、PSO算法，PSOGA 算法都具有更好的跟踪效果。因此，在对探测基座UMAC运动控制器的应用中，可以采用PSOGA 算法进行参数优化，使系统具有稳定时间短，误差小，更适合高速跟踪的特点。