旋转训练器旋转角度自适应调整方法研究

徐 京，付 超

（华北电力大学（保定校区）体育教学部，河北 保定 071003）

1 引言

训练器已经成为康复训练和运动训练的主要机械设备。其中，杠杆式旋转训练器凭借操作安全、结构简单、易于维修养护等优势被广泛应用。现阶段的训练器涉及了电子、动力学等领域。该器材的核心是动力传动设备，通常情况下由杠杆实现，而杠杆生成的阻力曲线有时无法满足人体发力曲线要求，再加上人们在使用训练器过程中，缺乏专业知识，使用设备方式不当，不利于康复和训练，甚至造成关节损伤。为进一步改进训练器性能，应设计一种功能全面、更加人性化的训练器。

文献［1］提出了基于摆动液压阻尼的训练器设计，通过研究生物力学特征，分析锻炼的最佳方式，研究基于摆动液压阻尼的训练方式，创造性地设计了基于阻尼大小输出的控制方式，并结合人体尺寸设计了训练器。但是该方法无法根据训练人员的实际情况进行实时调整，即无法达到自适应调整。文献［2］研究了动力学控制方法在训练器械领域应用，该方法分析了进乒乓球运动过程中动力学，涉及了训练器的动力学控制方法，实现训练器的优化，但是该方法的力特性分析效果不佳，导致优化效果低。

针对上述问题，并且从训练器的旋转角度着手，提出一种旋转角度自适应调整方法。针对训练器的结构特征，基于动力学思想计算肢体在不同方向上的运动速率，确定角度控制系统的硬件与软件设计；综合分析训练器受到的外界作用，将旋转角度利用非线性动力学表达式描述；设定训练器旋转角度的收敛条件和取值范围，通过设计的角度优化控制系统，实现旋转角度的自适应调整。该系统能够实时根据训练人员的身体素质和条件，自适应调整旋转角度，保证杠杆阻力符合人体发力需求，避免人体受到伤害。所提方法在促进康复训练的同时，推动了该技术的创新与发展，对我国训练机械水平的提高意义重大。

2 旋转角度自适应调整

2.1 旋转训练器结构分析

旋转训练器的整体结构分为机械系统与控制系统两部分［3］，其中，机械系统由旋转内圈、保护带、杠杆支撑轴、加速设备以及扶手组成。该器材能够训练人体感官的稳定性，改善人体机能，提高在旋转过程中的空间辨识力。

相比机械系统，控制系统的结构更加复杂，分为硬件与软件两部分。其中，硬件部分由控制器、传感器、显示器、角速度检测模块等子模块组成［4］。训练器控制系统硬件模块示意图，如图1所示。

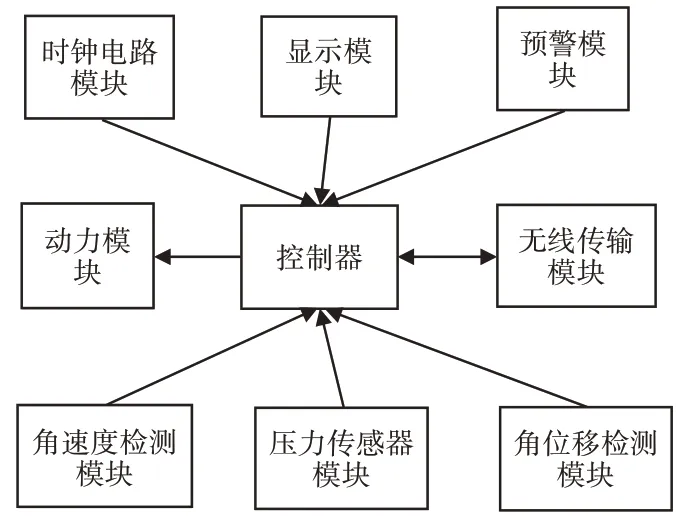
图1 训练器控制系统硬件模块示意图Fig.1 Hardware Module Diagram of Trainer Control System

根据图1可知，设计的训练器由多个模块组成，其具备数据量化直观性、便捷性和可调节性等。该系统可以有效检测角速度等，其采集的数据为软件系统提供计算依据。

2.2 旋转训练器元件组成

（1）电机选型：通常情况下训练器以步进电机作为运动控制元件，实现脉冲信号与角位移之间的转换。在低负荷运行状态下，电机转动速度和停止的方位取决于脉冲信号发出的频率，与电压波动并无直接关系。当电机获得输入信号时，自动转动一个步距离，因此，步进电机在满足负荷要求的情况下，可以迅速启停，转换精度高，且电路简单。

（2）驱动模块：DSP芯片可适应步进电机的外围功能电路，通过电压源控制电机转动速度，节省训练器空间，使控制系统的结构更加紧凑，便于使用。

（3）控制元件［5］：在所有执行元件中，电磁离合器是主要元件，因训练器使用过程中，其存在执行阻力和阻尼，离合器两侧的转速产生差异。为解决该问题，选取容易控制的摩擦片离合器。同时，训练器在阻尼影响下，驱动轴的转动速度应保持平稳，因此，离合器结合时间不能太短。选择的离合器具体参数包含额定动力矩23N·m、接通时间0.28s、额定电压24V、最大的转速0.32r/min、线圈直径0.22mm。

（4）角速度传感器：主要作用是测量驱动轴的转速，一般使用数字式传感器，同时设置A/D转换功能，增加中间电路，传感器的测速范围在千转以上。转速传感器主要技术参数为最大运行转速55r/min、每转频率88T/r、最大电阻1200Ω、最小电阻32Ω、最大工作电压63V。转速传感器既要解算元件，还需完成测速工作，因此，其误差要求苛刻，且需要输出电压保持稳定，这样才能满足训练器平稳运行的需求。若传感器不灵敏，导致测量结果出现较大的测量误差，无法为旋转角度的优化提供准确的依据。同时，标定和校正传感器，转速的单位是r/s，即每秒转盘所转过的角度。角速度传感器测量的是X、Y、Z三个轴转的角速度，将角速度传感器某一轴的数据除以2π就是当前这一轴所对应的转速。

2.3 自适应调整方法

在角度自适应过程中，利用动力学原理分析人体运动特征，构建旋转器的动力表达式［7］，定义旋转角的最佳取值范围并且增加补偿因子，优化自适应调整方法。具体操作过程如下。

假设不分析空气阻力对旋转角度产生的影响，此时人体运动只受重力影响。设置h表示身体运动高度，则垂直运动速率：

式中：θ—旋转角度。

在计算优化角度过程中，根据式（1）获得身体在水平方向的运动速率：

在人体执行前向运动时，可通过冲量定律计算肢体产生的旋转性质。身体运动达到一定高度后，利用V代表肢体旋转速率，则获得如下表达式：

式中：l—人体质量；v1—人体运动的初始速度；v2—人体运动的末速度；f0—人体受到的冲量［8］。

旋转训练器受到力的作用后开始运动，此时的训练器属于一个按照自身旋转规律逐渐向前的物体，受到重力、阻力等多种作用力的影响。

如果利用V'表示训练器运动速率，将角速度ω当作方向旋转角度，在训练器进行向下旋转时，由于外界力的作用，F描述的力的方向为向上方向，与身体运动轨迹的法向吻合，且和训练器位置具有存在关系，则力F的计算公式可变换为：

式中：E—旋转作用产生的升力指数；f—训练器旋转频度；fe—摩擦力。

为获得训练器横向旋转量、初始旋转速率等多个参量之间的关系，需要计算训练器的水平与垂直距离：

根据上述公式可得出在t时段内，旋转训练器在x和y方向的位移，则训练器旋转轨迹为：

完成距离计算后，利用下述公式获取不同方向位移、初始旋转速率和角速度之间的关系［9］：

基于动力学原理的旋转角度优化，因为不同轨迹的影响，需要建立训练器在旋转过程中的重力、浮力、阻力等动力方程，并计算参数之间的关系。计算旋转训练器总质量m'的数值，将建立的旋转角度优化模型变换为非线性动力学表达式：

式中：φ—训练器旋转位置。

若人体在训练时对杠杆式旋转训练器施加力，包括随机产生力度F1、侧力F2以及阻力F3，则利用下述公式计算每个力的具体数值：

式中：s—训练器在旋转时的迎风横截面积；cξ—随机力作用下的空气动力系数平均值；cη—侧力作用下的空气动力系数平均值；cp—阻力作用下的空气动力系数平均值。

结合上述分析，确定训练器旋转角度优化模型的收敛条件如下［10］

利用上述公式，根据杠杆式旋转训练器的基本物理参数，在满足模型收敛条件时，即可得到旋转角度的最优取值范围，完成自适应调整旋转角度，但是此时的旋转训练器的旋转角度自适应调整方法仍需要改进，通过CORDIC算法，优化旋转角度自适应调整方法。建立两个数组CS、XX，CS存储角度值，XX存储对应的余弦值。根据每一级旋转的剩余角度从CS与XX中选择最优的旋转角度与余弦值补偿因子。角度表达式为：

式中：i—第几次旋转；a(s(i))—第i次旋转的角度；n—数组的长度；s(i) ∈{0，1，2，…，n-1}。为了便于计算，令：

结合上述公式，获取迭代公式为：

Ln=为补偿因子。每一次旋转中，比较剩余角度的绝对值与数组CS 中的角度判断出此次旋转的最优角度值，并记录其余弦值，将每次旋转记录的余弦值相乘得到补偿因子Ln。通过上述优化后，实现杠杆式旋转训练器旋转角度动态优化方法的设计。

3 实验数据分析与研究

3.1 实验准备

为证明所提旋转角度自适应调整方法的可行性和有效性，设置实验平台，完成算法的性能测试。实验平台包括优化控制系统参数设置、串口通信、数据采集能功能。其中，串口通信获取杠杆的安全角度后，与PC端自动建立连接，将人体发力信息上传到中心系统。结束训练后，所有环节自动归位，回到初始状态，为后续训练做准备。实验以JK-QXZ-01旋转训练器为研究对象，实验参数，如表1所示。实验以结构摩擦性、动能、力与力矩为实验指标。实验研究对象，如图2所示。

表1 技术参数表Tab.1 Technical Parameter Table

图2 实验研究对象Fig.2 Experimental Subject

实验环境模型实际训练场所，温湿度通过室内空调控制在20℃和60%左右，并且实验采用了加速度传感器、角度传感器、转矩传感器获取实验数据，传感器具体参数，如表2所示。

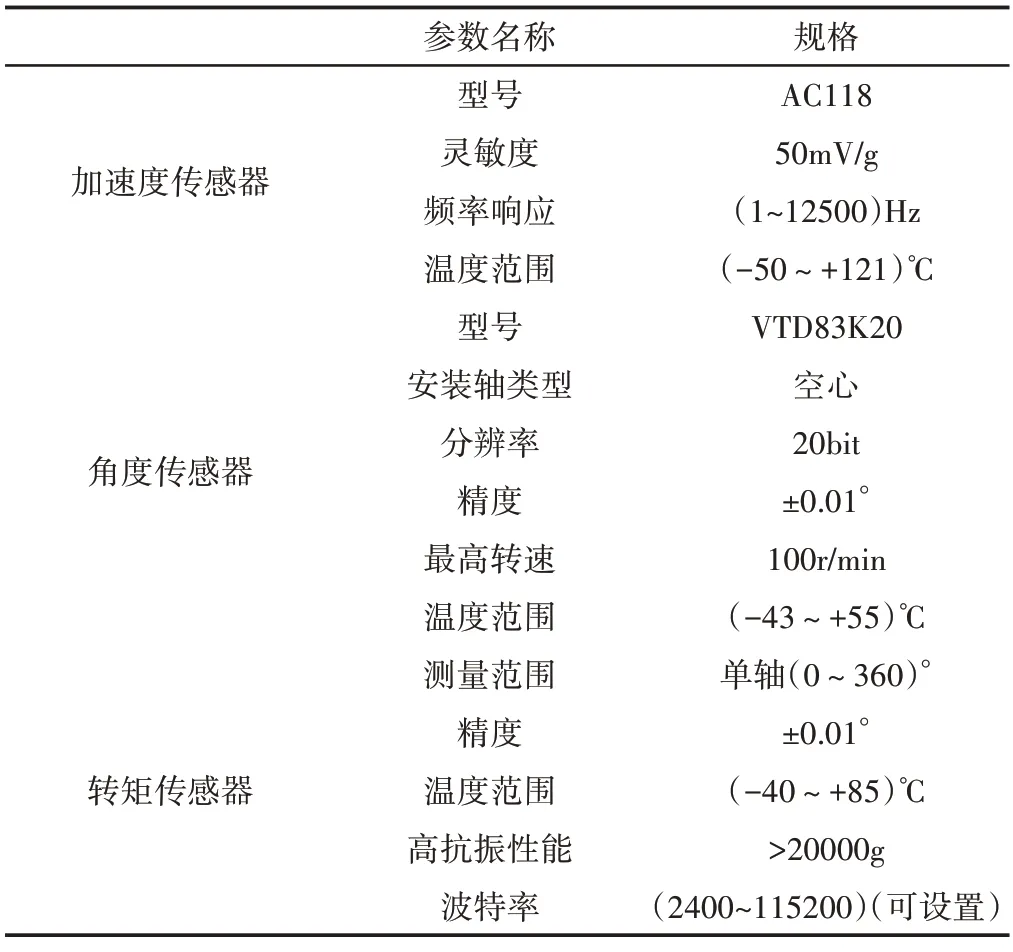
表2 实验设备信息Tab.2 Experimental Equipment Information

通过上述传感器采集实验所需的基础数据，并且将数据带入公式，获取测试的性能指标值，将指标值汇总成表格或者绘制成图，分析性能指标值，从而分析方法的性能。实验共进行35 次，实验通过连续采集的方式获取数据。连续性较强，具备更高的参考价值。同时，通过统计分析法，剔除采集数据中的异常数据，即过高和过低的数据，进一步提高数据的准确性，保障实验的有效性。

3.2 实验性能指标

实验以训练器结构摩擦性、旋转训练器动能和力与力矩为性能指标，各个指标的计算公式如下：

摩擦性能计算公式为：

式中：M1、M2、M3—三个杠杆的质量；

θ—旋转测量角度；

h—人体运动高度。

杠旋转训练器动能计算公式为：

式中：v0—加速度。

力矩的计算公式为：

式中：L—轴到着力点的距离矢量。

性能指标中训练器结构摩擦越低，表示设计方法的灵活度越高，其他指标越平稳，表明设计方法的性能越好。

3.3 实验性能测试

3.3.1 训练器结构摩擦性测试

实验选取的杠杆式旋转训练器目标共包括三组杠杆，分析应用选装角度自适应调整方法前后的摩擦性，该值越低，表明角度自适应调整方法越好。针对同一个设备进行反复测试，利用上述公式记录应用前和应用后训练器结构的摩擦性，以摩擦系数反应摩擦性能，实验具体结果，如表3所示。

表3 旋转角度优化前后摩擦性能对比Tab.3 Comparison of Friction Performance Before and After Optimization of Rotation Angle

根据表3 可知，旋转角度自适应调整前后的摩擦系数值随实验次数的增加而出现下降趋势，并且应用角度自适应调整方法后，测试点获取的摩擦系数值均低于应用前，同时，在实验次数为35 次时，摩擦系数值降到了0.28，其比优化前降低了0.08，因此，证明了该方法能够降低训练器的摩擦性，确保训练器旋转角度的灵活性，表明所提方法的角度自适应调整过程具备可行性。

3.3.2 旋转训练器动能测试

杠杆式旋转训练器各杠杆的运动惯性大，角度自适应调整的另一个目的是减少惯性，从而更加快速的进入稳定状态。因此，通过动能描述自适应调整前后杠杆式旋转训练器的动能情况，如表4所示。

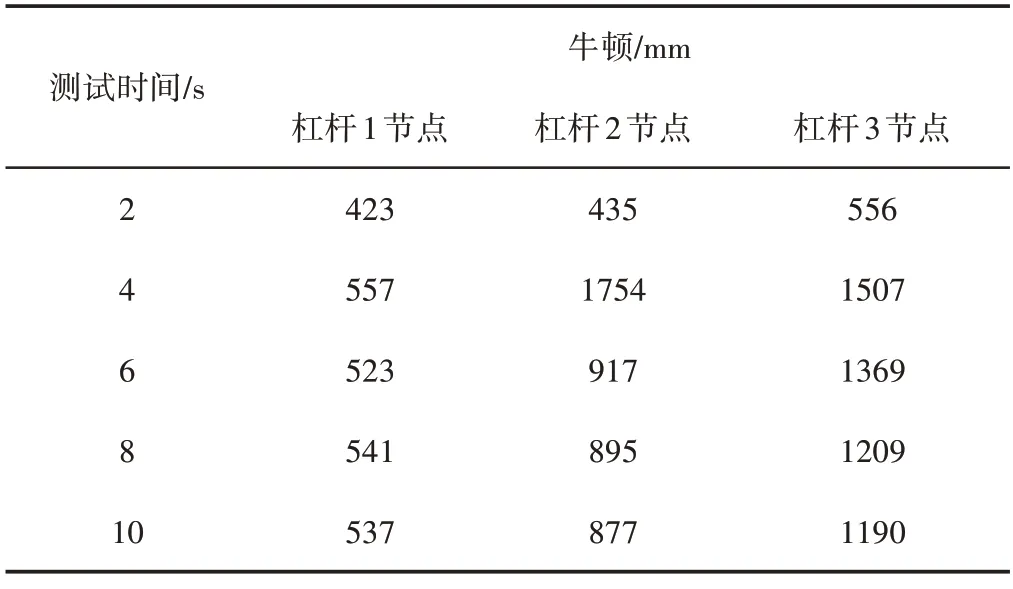
表4 训练器各杠杆动能曲线变化Tab.4 The Kinetic Energy Curves of Each Lever of Trainer Change

由表4可知，为减少惯性，保证训练器的平稳性，在杠杆底座位置和地面间设置固定副，此时底座角速度等于零，因此，动能也基本为0，这一现象符合训练器的实际使用状况。在6s的时候，各杠杆的动能基本处于平稳动态，达到匀速训练状态，杠杆1节点稳定在540mm左右，杠杆2节点稳定在900mm左右，杠杆3节点稳定在1250mm左右，没有大幅度的震动。因此，表明说明了所提优化方法能够快速使训练器进入平稳训练状态，始终保持过程平稳。

3.3.3 力与力矩测试

杠杆受到的力和力矩也是评价旋转角度优化效果的重要参数，因为，旋转角度优化后，如果力和力矩波动较大，容易导致训练人员的作用力变化较大，达不到训练的目的，甚至导致人员受伤，因此，需要测试角度优化后力和力矩的波动情况。不同杠杆在x轴的实验测试结果，如表5、图3所示。

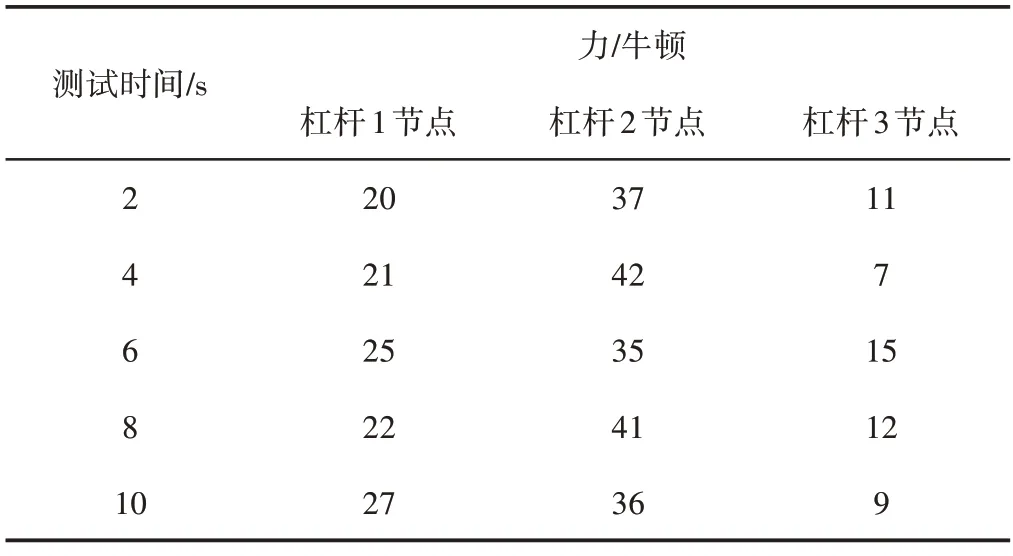
表5 力测试结果Tab.5 Force Test Result

图3 力矩测试图Fig.3 Torque Test Diagram

分析表5、图3可知，力测试的数据波动较小，其中杠杆1节点的波动最小，其最大波动仅为5N，力矩前期存在一定波动，但是后期趋于稳定。因此，每个杠杆在训练器运动过程受力情况变化不大，且每个力矩随测试时间推移，变化平滑，并无突变现象产生。因此，在设计的旋转角度自适应调整后，该方法能够动态控制力和力矩的变化情况，避免发生意外现象。

4 结论

针对旋转训练器存在的局限性，为了提高旋转训练器的性能，提出了旋转训练器旋转角度自适应调整方法。

（1）基于动力学原理，分析了旋转角度控制系统，通过设定合理的旋转角范围和设置补偿因子，实现旋转角度自适应调整。

（2）在6s的时候，各杠杆的动能基本处于平稳动态，达到匀速训练状态，没有大幅度的震动。因此，表明说明了所提优化方法能够快速使训练器进入平稳训练状态，始终保持过程平稳。所提方法有效减少训练器结构摩擦力，摩擦系数值降到了0.28，其比优化前降低了0.08，训练器的性能更加优越。

（3）验证分析了旋转训练器的动能，其在6s的时候，各杠杆的动能基本处于平稳动态，达到匀速训练状态，杠杆1节点稳定在540mm左右，杠杆2节点稳定在900mm左右，杠杆3节点稳定在1250mm左右，没有大幅度的震动。因此，该方法可以使训练器快速进入稳定状态。

（4）力测试的数据波动较小，其中杠杆1节点的波动最小，其最大波动仅为5N，力矩前期存在一定波动，但是后期趋于稳定。确保了力和力矩的变化平稳，避免出现突变情况，为训练器的安全使用提供保障。

（5）在今后研究中，深入旋转训练器的数据采集，进一步提高采集精度，优化旋转角度自适应调整方法。