CFRP板倾斜冲击损伤的非线性超声评价

郭 建，李 成，铁 瑛

（郑州大学机械与动力工程学院，河南 郑州 450001）

1 引言

由于较高的强度重量比与良好的抗疲劳性等特点，碳纤维增强聚合物（CFRP）板在关键工程结构中被广泛使［1］。但是在服役期间由于碎屑的撞击、工具掉落等，都会使其内部产生不可见的冲击损伤，并对结构安全性产生潜在的威胁［2］，因此采用非破坏性技术来检测初始损伤并对其损伤程度进行评估就显得尤为重要。

非线性Lamb波近年来被越来越多的学者用于复合材料冲击损伤的检测中。文献［3］利用试验研究的方法，通过将不同冲击能量损伤的非线性参数进行对比，提出了可用二次谐波法检测复合材料冲击损伤。文献［4］通过组合导波混合技术和混合频率峰值计数方法对CFRP板中冲击损伤进行评估，结果表明混合频率谱峰数与冲击能量的相关性呈单调增长。文献［5］利用非线性Lamb波预测层压板中的几乎不可见冲击损伤，并建立了相对声学非线性参数统计概率分布的数学模型，以对损伤进行预测。文献［6］提出了两种复合材料冲击损伤检测的建模方法，用应力的变化来表示Lamb波的传播，并分别研究了不同程度损伤对Lamb波传播的影响。

现有文献主要对垂直冲击损伤的检测进行研究，而对倾斜冲击损伤的无损检测的研究较少。为此，利用ABAQUS 软件通过添加粘性力抑制冲击过程产生的振动实现了冲击后的检测，建立了CFRP板低速冲击-检测的全过程仿真模型，并通过频散曲线对激励频率进行选择。再与试验结果对比，验证有限元模型的正确性，利用模型进一步探讨了不同冲击角度的冲击响应，以及冲击角度与信号接收的距离对相对非线性系数（RANP）的影响。

2 低速冲击损伤与检测试验

试验包括落锤冲击试验与对受损试件进行的非线性Lamb波检测两部分。试件为T300/7901型CFRP板，铺层顺序为［0/90］3s，尺寸为（200×100×2.4）mm。CFRP板及胶层的材料参数［7］，如表1所示。

表1 材料参数Tab.1 Material Properties

以ASTM D7136/D7136-07为标准，采用XBL-300型落锤冲击系统进行低速冲击试验，同时保证冲击中心始终在CFRP板中心。其中冲头为前端直径25mm的2.0kg半球，通过调节冲头与CFRP板间的距离来实现对冲击初始动能的控制；试验时冲头所受的力经由传感装置采集并传递给电脑。不同能量的冲击试验均进行三次。

非线性Lamb波在CFRP板中进行传播时所具有的频散特性和多模态特性，导致了在特定频率下至少存在两个不同的模态，而不同的模态对损伤的响应行为不同，该特性将直接影响检测结果。利用DC 软件所绘制的上述CFRP 板的频散曲线，如图1 所示。可以看到在小于A1模式截止频率的频域前只存在A0和S0两种模态，因此为避免过多模态所引起的能量耗散，选较低频率作为激励频率，考虑到试验条件，取激励频率为0.5MHz。

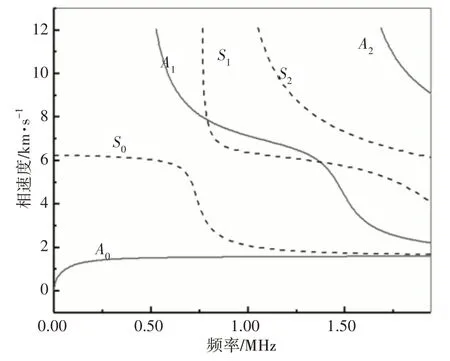
图1 CFRP板频散曲线Fig.1 Dispersion Curves of CFRP Plate

采用RITEC RAM-5000 SNAP 超声检测系统对经过冲击的CFRP板进行非线性检测试验，检测系统示意图，如图2所示。激励信号经过衰减器、低通滤波器（0.5MHz）后通过45°斜楔形换能器在试件进行传播；接收换能器接收到的信号经由高通滤波装置（1MHz）传输到示波器，通过计算机处理得到信号的频域图。采用的激励信号为10周期0.5MHz的Hanning窗调制信号，并保证检测距离始终保持在100mm。

图2 非线性超声检测平台Fig.2 Nonlinear Ultrasonic Detection Platform

3 低速冲击损伤与检测仿真模型

在ABAQUS 软件建立冲击-去振动-Lamb 检测的一体化模型，该模型包括三个分析步：冲击进程、冲击后的振动消除、检测。CFRP板的尺寸设置为（200×100×2.4）mm，铺层为［0/90］3s。其中采用连续壳单元对CFRP板建模，并约束冲头为刚体，最后在各层之间添加零厚度粘性单元以模拟层间胶层，采用二维Hashin准则和内聚力模型预测CFRP板层内与层间的损伤触发与演化。

对于冲击进程，设置冲头与CFRP板为面面接触，将板的四周完全固定，并给冲头一个Z方向的初速度以模拟垂直冲击时的状态。为了简化模型同时保证检测步骤的精度，设置冲击-检测区域网格尺寸为（0.2×0.2）mm，其他区域网格尺寸为（0.5×0.5）mm，并保证碰撞位置在CFRP板的中心。

冲击后CFRP板的振动会对检测精度产生影响，这也是大部分文献只在试验上对冲击损伤进行检测的原因。为了保证Lamb波的施加与接收的正确性，提出在冲击后引入一个载荷分析步以抑制冲击所产生的振动。分析步中通过对板施加粘性压力，使板在短时间达到准静态平衡状态，粘性压力的大小定义为［8］：

式中：p—施加到CFRP板表面的压力；

cv—粘度；

ν—所施加粘性力表面点的速度矢量；

n—表面向外的法向矢量。

在非线性Lamb波检测分析步，设置增量步为1×10-8s。由于S0模态对厚度损坏和分层的敏感性更大［9］，因此采用等效轴向位移模拟S0模态的Lamb波激励信号，其表达式为：

式中：A—调制波幅值；

t—Lamb波的传播时间；

V—施加位移的最大值；

fc—激励信号的中心频率；

N—窗函数的循环周期数。最终的冲击-检测模型，如图3所示。

图3 冲击-检测模型Fig.3 Impact-Detection Model

在小应变的情况下，如果忽略传播过程中的衰减，则Lamb波在各向同性固体中一维非线性波动方程近似解为［10］：

式中：A1，A2—接收点的基波和二次谐波的振幅；k—波数；x—信号传播的位移；β—非线性Lamb波系数。

由于在一定的试验条件下，k与x为定值，因此可以将式（3）简化为：

这里用β'来表示含冲击损伤的CFRP板的超声非线性，并用RANP代替。

4 结果分析与讨论

4.1 仿真模型的验证

分别用0J，10J，14J 的初始能量对CFRP 板进行垂直冲击-检测仿真与试验，并对比试验与数值仿真结果的冲击力-时间曲线以及不同能量的冲击损伤下产生的高次谐波，以验证模型的正确性。不同初始能量的冲击力-时间曲线的仿真与试验结果对比，如图4所示。通过图可以看出初始能量为10J时，冲击力的峰值分别为3.45kN和3.72kN，误差7.8%；初始动能为14J时，冲击力的峰值分别为4.6kN和4.8kN，误差4.3%。此外仿真与试验的冲击力随时间的变化趋势也相一致，以上结果充分说明有限元模型在冲击进程的准确性。仿真模型中随机选取的四个点在冲击分析步和去振动分析步的位移变化，如图5所示。由图可以看出，冲击进程结束以后CFRP板一直处于振荡状态，而经过去振动后，所有随机点的振动迅速消除，这也为Lamb波的施加提供了条件。

图4 不同初始动能的冲击力曲线Fig.4 Impact Force Curve of Different Energy

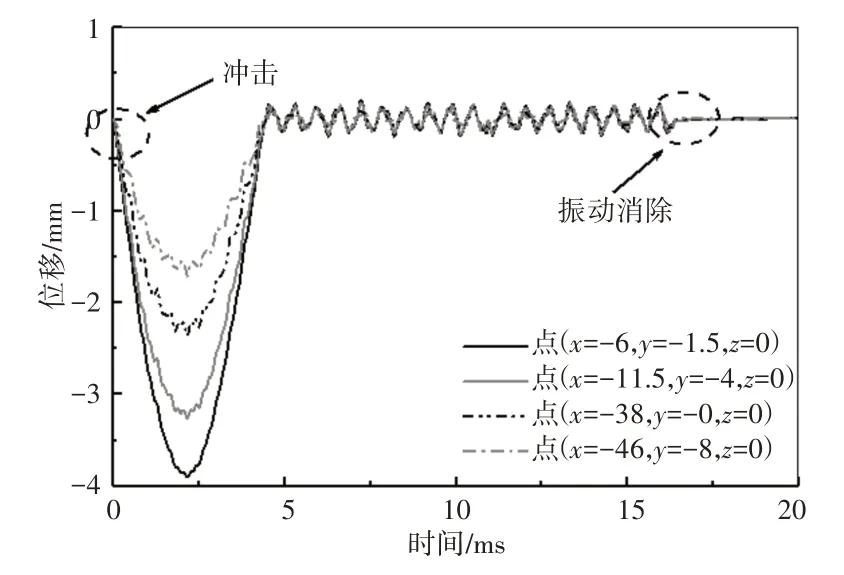
图5 随机点的位移与时间的关系Fig.5 Displacements Versus Time of Random Nodes

提取三种能量下仿真和试验所得到的时域信号，并分别对信号进行FFT变换和归一化处理得到频域图。不同冲击能量下所测得的CFRP 板的仿真与试验结果的频域信号（基波信号位于0.5MHz，二次谐波信号位于1MHz），如图6所示。图6（a）显示相较于无损板，试验过程中含冲击损伤的CFRP板产生了较大的二次谐波信号，且随着冲击能量的增加所测A2值也逐渐变大。而图6（b）可以看出，仿真得到了相同的结果，冲击损伤的增大使试件表现出更大的非线性。以上结果表明所建立的数值模型可以有效的模拟冲击损伤的非线性检测。

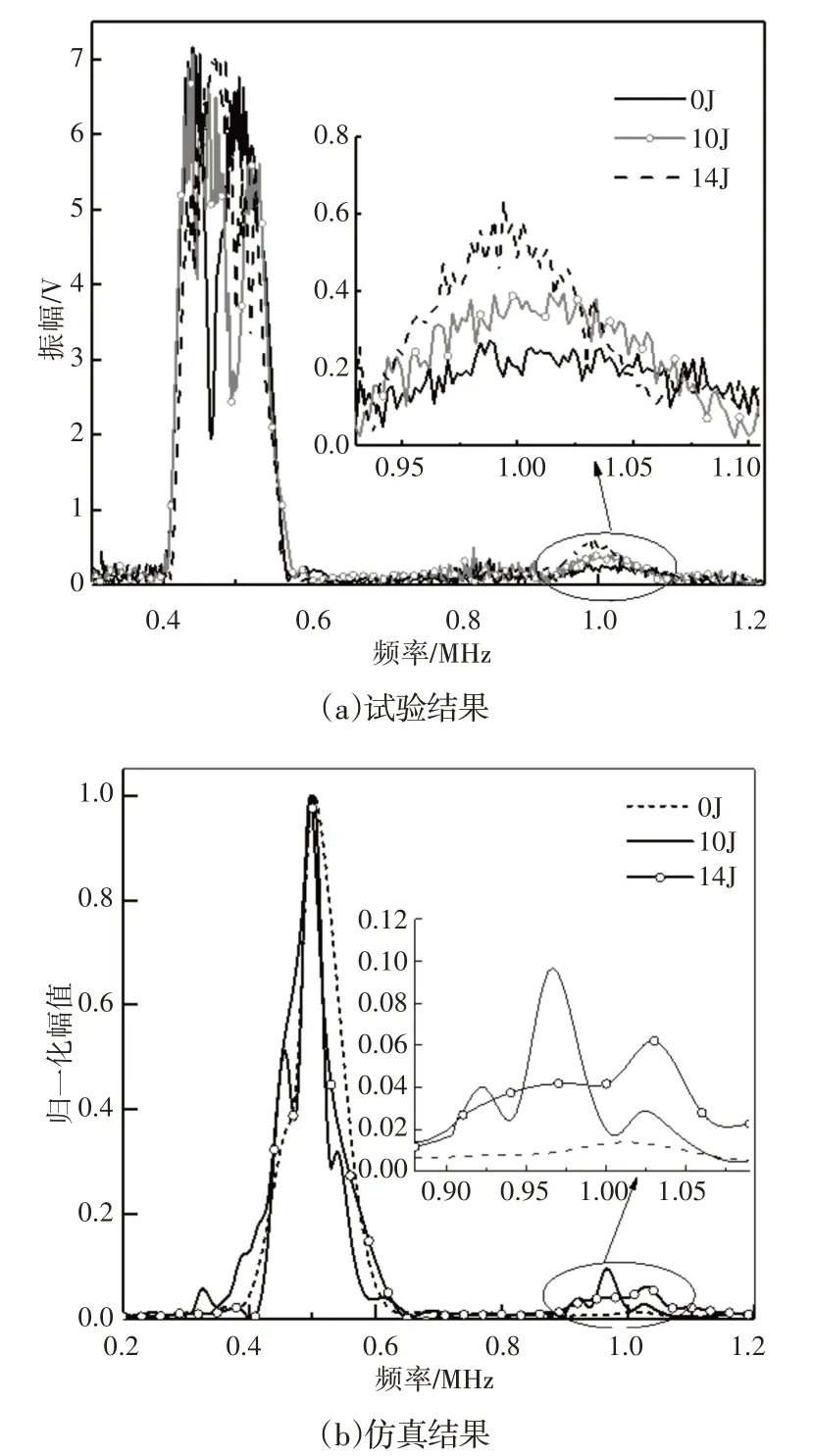
图6 不同初始动能下频域图对比Fig.6 Frequency Domain Diagram Under Different Energy

4.2 冲击角度对RANP的影响

为了研究不同的冲击角度对Lamb 波非线性的影响，保持CFRP 板处于水平，将冲头沿Y轴方向的中心轴进行旋转，将冲头方向的旋转角定义为冲击方向。为了减小检测误差，仿真时保证冲击中心始终处于板的中心位置。倾斜冲击的示意图，如图7 所示。（其中，θ为冲击角度）。控制冲头初始动能始终为14J，设置冲头速度为3.741m/s。分别设置θ的值为0°、15°、30°、45°、60°对CFRP 板进行冲击-检测的仿真，并对仿真结果进行处理、分析。

图7 倾斜冲击示意图Fig.7 Schematic Diagram of Oblique Impact

4.2.1 不同冲击角度下CFRP板的冲击行为

CFRP 板在冲击载荷下的能量吸收是广泛研究的重要参数之一。由于CFRP板最终吸收的能量主要为损伤耗能，因此可用此来判断冲击损伤的大小。CFRP板吸收的能量随时间的变化，如图8所示。

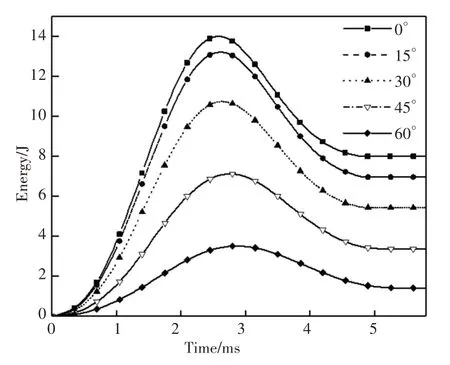
图8 不同θ值下CFRP板能量吸收曲线Fig.8 Energy Absorption Curve of Different θ

可以看出，CFRP板吸收能量的峰值与最终吸能均与θ值负相关。当冲击角度为60°时吸收能量的峰值与最大值分别为3.51J 与1.42J，仅仅为正冲时两参数的25%、17.7%。这种结果产生的原因是倾斜冲击过程中冲头存在垂直和水平两个方向的分速度，因此在达到最大损伤的时刻，冲头速度并不为零。随着θ值的增加，冲头的垂直分速度逐渐减小，水平分速度相应增大，这就导致了图8 中吸收能量的最大值处于下降趋势，且下降速率逐渐增大。与此同时，θ值的增大也使冲击进程的时长相应的增加。相较于纤维和基体，复合材料的胶层较容易产生损伤，因此可用层间分层情况表示不同冲击角度所造成损伤的大小。不同θ值所引起的CFRP 板的所有层间损伤沿厚度方向的包络图，如图9 所示。通过图片对比可知，随着θ值的增大，其分层损伤逐渐减小，当θ为60°时，其分层损伤的大小仅为垂直冲击时的1/4。这与CFRP 板吸收能量的大小得出的结论一致。

图9 不同θ值下CFRP板的分层损伤Fig.9 Delamination Damage of Different θ

4.2.2 不同冲击角度下的RANP

将接收点处的位移时间数据作为接收信号，并对不同角度冲击下接收点所接收到的时域信号进行快速傅里叶变换和归一化处理得到频域信号，通过比较A1与A2的变化情况分析其非线性现象。

冲击角度为0°（垂直冲击）、60°时所接收到时域信号，如图10所示。不同冲击角度下的接收信号经过FFT变换后得到的频域波形图，如图11所示。可以发现，接收信号的波形与冲击角度有关，θ值的增加会导致第一个波包幅值的明显增大。经过归一化处理后，1MHz附近的二次谐波幅值对冲击角度的变化很敏感，当冲击角度由0°变化到60°时，其幅值由0.097变化到0.025。所以二次谐波幅度可以大致表征冲击角度，但是由于RANP值是基波幅度和二次谐波幅度综合性能的表现，因此通常被用来表征材料的非线性效应。

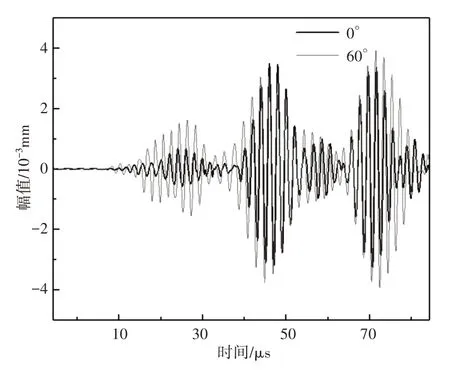
图10 不同θ值的接收信号时域图Fig.10 Time Domain Diagram Under Different θ

对不同冲击角度下的接收点信号进行处理，分别计算其RANP 值，并绘制RANP 与冲击角度的关系曲线，如图12 所示。可以看到，随着θ值的增加，CFRP板的RANP出现变化，并处于减小态势。同时结合冲击损伤的分析结果可知，出现这种结果的原因是冲击角度的增加导致了损伤的减小，当Lamb波经过冲击损伤区域时，原始波形由于材料损伤程度的不同而发生变化，从而导致了RANP的变化。因此可以通过RANP的大小来反映冲击损伤程度，从而对CFRP板的健康状况进行无损监测。

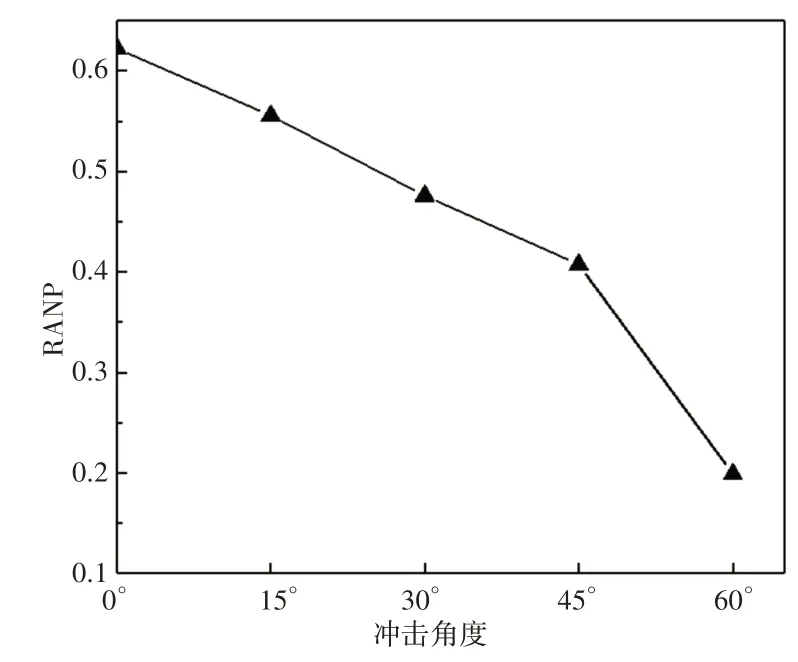
图12 不同冲击角度下的RANPFig.12 RANP Under Different Impact Angles

4.3 信号接收距离对RANP的影响

为探究信号接收距离对非线性系数的影响，在冲击角度为0°的冲击损伤模型中，设置信号接收点与损伤中心点的初始间隔为40mm，保持信号激发点位置不变，并每隔10mm设置一组信号接收点，分别对接收点接收到的时域信号进行FFT处理。不同检测距离下测得的A1、A2与RANP，如表2所示。

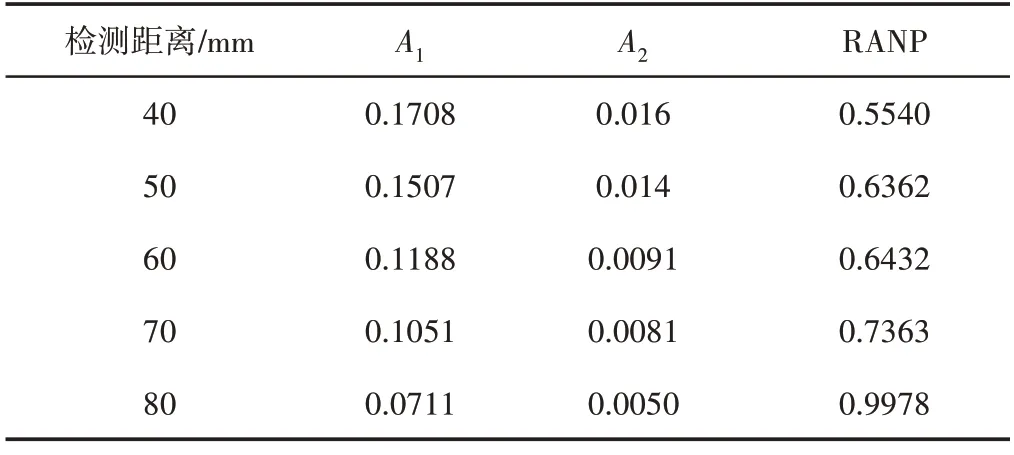
表2 不同参数随检测距离的变化Tab.2 Variation of Different Parameters with Distance

从表2 可以看到，随着距离的增加，A1、A2均相应变小，而RANP的变化趋势相反。造成这种结果的原因是：CFRP板的各向异性使得非线性效应随距离增加而逐渐增大，导致更多的能量从基波向高次谐波转移，再加上Lamb波传播中能量的衰减共同导致了基波与二次谐波幅值的减小。从表中很明显可以看出，A2的变化幅度相较于A1较小，这就使RANP值增加。

5 结论

针对CFRP板的倾斜冲击损伤检测问题，建立了从低速冲击到损伤后进行非线性超声检测的全过程仿真模型，并应用非线性Lamb波响应对损伤进行评估，结果表明：

（1）通过试验验证了CFRP板冲击-去振动-检测一体化模型的正确性。

（2）随着冲击角度的增加，CFRP板吸收能量峰值及最终吸收能量值均逐渐减少，分层损伤也逐渐减小。

（3）RANP与冲击角度负相关，因此可以通过对比RANP值对不同冲击角度的损伤进行评估。

（4）检测距离对信号接收有重要的影响。在一定的距离范围内，A1与A2的幅值均随检测位置相对损伤的距离的增加逐渐减小，而RANP则逐渐增大。