多通道信息融合与深度迁移学习的旋转机械故障诊断

张龙　胡燕青　赵丽娟　张号

摘要：针对单通道信号特征信息不充分的问题，提出了一种多通道信息融合与深度迁移学习的旋转机械故障诊断方法。首先使用小波变换将多传感器采集的一维信号生成多幅时频图，然后将时频图信息融合为多通道图像，最后将预训练的深度残差网络作为迁移模型对旋转机械进行故障诊断。圆柱滚子轴承、某局机务段机车轴承和齿轮箱数据集的识别准确率分别为99.23%、99.78%和99.50%，凯斯西储大学轴承数据集的跨工况迁移试验识别准确率达93.12%，这表明所提方法具有一定的优越性和可扩展性。

关键词：故障诊断；旋转机械；多通道信息融合；深度迁移学习

中图分类号：TH13；TH17

DOI：10.3969/j.issn.1004-132X.2023.08.011

Multichannel Information Fusion and Deep Transfer Learning for Rotating Machinery Fault Diagnosis

ZHANG Long HU Yanqing ZHAO Lijuan ZHANG Hao

State Key Laboratory of Performance Monitoring Protecting of Rail Transit Infrastructure，East China Jiaotong University，Nanchang，330013

Abstract： To address the problems of inadequate information on the characteristics of single channel signals， a rotating machinery fault diagnosis method of multichannel information fusion and deep transfer learning approach was proposed. Firstly， the one-dimensional signals collected by multi-sensors were used to generate separate time-frequency maps by wavelet transforms. Then， the information of the maps was fused into multi-channel images. Finally， the pre-trained deep residual network， as a transfer model， was used for fault diagnosis of the rotating machinery. The identification accuracy of the tests on the cylindrical roller bearing， locomotive bearing， and gearbox datasets of a bureau of locomotive section is as 99.23%， 99.78%， and 99.50% respectively； and the identification accuracy of the cross-service transfer tests on the Case Western Reserve University bearing dataset is as 93.12%， which indicates the superiority and scalability of the proposed method.

Key words： fault diagnosis； rotating machinery； multichannel information fusion； deep transfer learning

0 引言

旋轉机械长时间在重载和高速的条件下工作时，不可避免会产生故障，进而影响设备的正常运行和使用，因此，研究旋转机械的故障诊断方法对保证工业设备的正常运转具有重要意义。

传统的故障诊断方法中，使用傅里叶变换、小波变换、经验模态分解等信号处理方法进行故障特征的提取最为常见，但单一的信号处理方法故障诊断的识别精度并不理想，因此有学者开始结合信号处理与机器学习进行故障诊断，并取得了一定的进展，但神经网络等传统浅层网络结构限制了高维度、非线性特征的学习能力。

深度学习网络具有强大的特征自适应提取能力，克服了传统故障诊断算法的缺点，通过端对端的处理，能在一个模型中完成特征提取与故障诊断，因此广泛用于故障诊断领域［1-2］。然而深度学习网络的分类性能受网络层数的影响：随着网络层数的增加，提取到的特征维度增高，获得的信息增多，但网络层不能简单叠加，否则会出现梯度弥散或梯度爆炸，导致模型的识别准确率下降，训练时间变长。

深度迁移学习将深度学习网络的特征提取能力与迁移学习的先验“知识”［3-4］相结合，在传递先验“知识”的过程中能避免模型训练时出现大量不必要的重复工作［5］。迁移学习中，模型和参数的传递［6］能在预训练模型的基础上，根据目标域的特征进行适应性的微调，不仅能大量缩短深度学习网络模型的训练时间，还能高效获得稳定的训练结果。于是一些学者将迁移学习引入故障诊断领域。ZHANG等［7］提出了一种基于神经网络的迁移学习方法，即先从海量源数据中学习特征并适应性调整神经网络的参数，再使用少量目标数据训练新模型进行故障诊断从而获得较高的识别精度。陈仁祥等［8］利用少量目标标记样本微调深度置信网络的预模型网络权重与偏置值，提高了行星齿轮箱的小样本故障诊断准确率。上述研究的输入特征是单通道灰度图像，有学者为充分发挥深度学习网络提取图像特征的优秀性能，将多通道图片作为特征输入。SHAO等［9］利用ImageNet上预训练的VGG网络模型，通过复制时频图来增加通道数并采用微调网络策略，取得了较高精度的诊断结果。刘飞等［10］采用结合傅里叶变换与伪彩色处理的方法扩充通道数，利用迁移预训练模型实现了滚动轴承故障的快速诊断。

上述这些方法仍然只使用单个传感器的故障信号，仅对一个源信息进行加权变换，没有充分利用数据集中的所有信息进行特征融合故障诊断，导致所提的故障诊断模型泛化性能弱，只在特定场合下取得较高的识别准确率。为更加全面地提取故障信号的隐含特征，SHE等［11］将多个传感器信号输入多通道一维卷积神经网络，取得了较高的故障识别精度，但多通道一维卷积神经网络无法充分发挥神经网络提取图像特征的性能，且没有深入研究多传感器信号的信息融合，因此会影响故障诊断的效果。

基于上述分析，本文提出了一种基于多通道信息融合与深度迁移学习的旋转机械故障诊断方法。首先使用小波变换将3个传感器采集的信号转换成时频图，随后进行信息融合组成RGB三通道，将一维故障信号转换成多通道图像。然后，采用多通道信息融合方法生成的图像，使多通道信息融合与深度迁移学习（multichannel information fusion and deep transfer learning，MIF-DTL）充分提取图像中的隐含特征。最后，通过迁移学习进行模型和参数的传递，以大幅缩短应用深层深度学习模型的时间，获得准确、稳定且高效的故障诊断结果。

1 方法介绍

1.1 连续小波变换

连续小波变换克服了短时傅里叶变换的缺陷，在信号的时域和频域均具备较好的局部刻画能力。小波变换通过伸缩和平移等运算可对函数或信号进行多尺度的细化分析，是一种有效的信号时频分析工具。小波变换的原理如下：假设振动信号x（t）∈L2（R），则小波变换可表示为

式中，ψa，b（*）表示小波函数簇，可由小波母函数ψ（*）得到；a、b分别为尺度参数和时移参数，a，b∈R，a>0。

对信号进行连续小波变换的数学表达式为信号x（t）与小波的簇函数内积运算。利用小波变换将信号与滤波器进行卷积处理是分析非平稳性信号的一种时频分析方法，可用于故障特征提取，并能有效提取振动信号中微小缺陷的弱脉冲信号。Morlet小波的时域波形与轴承的振动信号故障冲击波形相似，因此本文选用Morlet小波基函数。

1.2 深度殘差网络

增大神经网络的层数会导致梯度弥散或梯度爆炸，降低模型训练准确率。而深度残差网络（deep residual network，ResNet）通过构建残差块（图1）来建立残差连接，在一定程度上消除了梯度弥散和梯度爆炸。

残差块的作用是当网络达到最优状态时，通过进一步深化网络结构将残差映射压缩为零，只留下恒等映射。恒等映射的编排方式允许梯度在网络中进行跨层传播，识别每一层的输入，学习并形成残差函数，有效降低模型的学习难度，加快模型的收敛。理论上，随着神经网络层数的增加（大于100层），网络性能不会出现退化，将保持在最佳状况。ResNet-18的结构参数如表1所示。

1.3 迁移学习

迁移学习是一种利用应用场景中的相关知识来提高目标场景中的学习性能的方法。迁移学习的目的是找出不同任务或领域间的共性特征［12-13］。迁移学习的定义［14］如下：域D由特征空间χ和边缘概率分布P（X）组成，其中，X={x1，x2，…，xn}∈χ。迁移学习指的是将学习源域Ds={Xs，P（Xs）}和源任务Ts={Ys，fs}中提取的知识应用到目标域Dt={Xt，Q（Xt）}和目标任务Tt={Yt，ft}，决策函数ft在目标域Dt中的表现反映了知识应用的程度，其中，Ds≠Dt或Ts=Tt。

参数迁移学习的基本思想是让目标域Dt和源域Ds的模型共享参数，它在神经网络上对预训练模型的参数进行微调，实现模型的参数更新［15］，与其他方法相比，这避免了直接使用辅助数据带来的分布误差。从模型训练的角度来看，参数迁移学习的优势在于无需改变模型的结构，只需对预训练模型的参数进行适应性的微调就能匹配目标域Dt的特征分布。这既可以显著缩短模型的训练时间，又获得稳定、高效的深度学习网络模型。网络的微调基于目标域Dt的数据集（实验数据集），因此参数微调后的模型更适应实验数据集。

基于此结论，本文通过迁移学习进行模型和参数的传递，使用可视化数据库ImagNet上预训练的ResNet模型，在不改变模型结构的前提下，让网络针对旋转机械图像特征进行适应性的参数微调。

2 多通道信息融合故障诊断方法

本文提出一种基于MIF-DTL的旋转机械故障诊断方法。该方法能自适应提取旋转机械的故障特征，具有泛化能力强、识别效果精确、诊断速度快的特点，方法框架如图2所示。

基于MIF-DTL的旋转机械故障诊断方法分为如下三个步骤：

（1）多通道信息的数据处理。首先使用小波变换对数据集中采集到的3个信号进行时频图变换，然后采用多通道信息融合处理，组成三通道RGB彩色图像。

（2）预训练模型迁移。利用迁移学习的方法，将预训练于ImageNet可视化数据库的ResNet18模型用于旋转机械的故障诊断。

（3）自适应故障诊断。保持预训练的模型结构不变，让网络针对旋转机械图像特征进行适应性的参数微调；对于全连接层的最后一层，将输出特征值改为试验的故障识别种类数。

将训练集与验证集数据输入模型，通过10次迭代对参数进行微调，得到稳定的模型，再对测试数据集进行故障诊断，并将结果作为模型的故障诊断识别率。

3 案例研究与实验结果分析

本节对圆柱滚子轴承数据集［16］、JL-501机车轴承数据集［17］和齿轮箱数据集［18］进行故障诊断分析。实验运行的软件环境为windows10 64位操作系统，运行内存为16G，在PyCharm平台上使用Pytorch框架，硬件环境为AMD Ryzen 7 5800H，RTX 3070 Laptop GPU显卡。

在诊断模型的训练过程中，深度学习模型训练的迭代次数、批数、Adam学习率分别设为10、32和0.0003。

为避免偶然误差，将10次试验的平均值作为最终结果。试验数据的训练集、验证集和测试集按照6∶2∶2的比例随机划分。多通道信息与迁移学习故障诊断试验中，模型“A”使用加速度传感器a采集数据，并利用“小波变换+伪彩色处理”［15］的方法构造多通道图像样本；模型“A+B”是3个通道（通道1、2分别使用加速度传感器a、b采集的数据，通道3使用加速度传感器a、b数据的平均值）分别利用小波变换生成时频图，然后将时频图信息融合为多通道图像样本。

3.1 圆柱滚子轴承故障诊断（案例1）

案例1选用圆柱滚子轴承数据［16］，由三轴加速度计PCB3456A01在轴速2050 r/min、采样频率70 kHz下采集轴承座的垂直（通道Ⅰ）、水平（通道Ⅱ）和轴向（通道Ⅲ）振动数据。轴承设置内圈故障、外圈故障、滚动体故障，且每种故障都有4种不同程度的损伤。

3.1.1 数据集的预处理

对圆柱滚子轴承数据集中的振动信号使用无重叠分割。如表2所示，構造的实验样本（每个样本由2048个数据点构成）共有13种健康状况，包含1类正常样本和12类故障样本。

3.1.2 Morlet小波基函数的参数确定

实验开始前需要确定Morlet小波基函数的详细参数，利用表2中的数据，分析了尺度序列长度和中心频率对MIF-DTL模型准确率的影响，结果见表3、表4。

由表3可以看出，本文方法在尺度序列长度224时准确率最高。尺度序列长度与深度网络特征图的输入大小相匹配，尺度序列长度过小或过大都会导致故障特征图信息丢失或忽略，降低识别准确率。由表4可以看出，本文方法在中心频率0.8125 Hz的识别准确率最高。中心频率过高或过低都会影响小波变换的效果，降低特征图的质量。故本文小波变换使用morlet小波基函数，其中心频率设为0.8125 Hz［24］，尺度序列长度设为224。

利用多通道信息融合方法，对表2中标签为D1、D2、D6和D10的4类样本进行时频图可视化，结果如图3所示，可以看出，不同故障类型的轴承时频图存在显著差异。

3.1.3 多通道信息与迁移学习故障诊断实验结果

如图4所示，MIF-DTL对故障的最大识别准确率为99.42%，最小识别准确率为99.04%，平均识别准确率为99.23%，标准差为0.17%，故障识别准确率高于其他方法。

在3种单传感器的故障诊断模型实验中，故障诊断模型B的表现最好，但其识别准确率远低于MIF-DTL。融合2个传感器的数据信息进行故障诊断的效果优于单个传感器。故障诊断模型A+C的最大识别准确率为98.65%，最小识别率为97.69%，平均识别准确率为98.15%，标准差为0.26%，但其模型识别准确率和稳定性均低于MIF-DTL。

多通道信息融合（multichannel information fusion，MIF）的故障诊断模型中，最大识别准确率为95.38%，最小识别率为94.04%，平均识别准确率为94.67%，标准差为0.39%，但其识别准确率和稳定性均低于MIF-DTL。

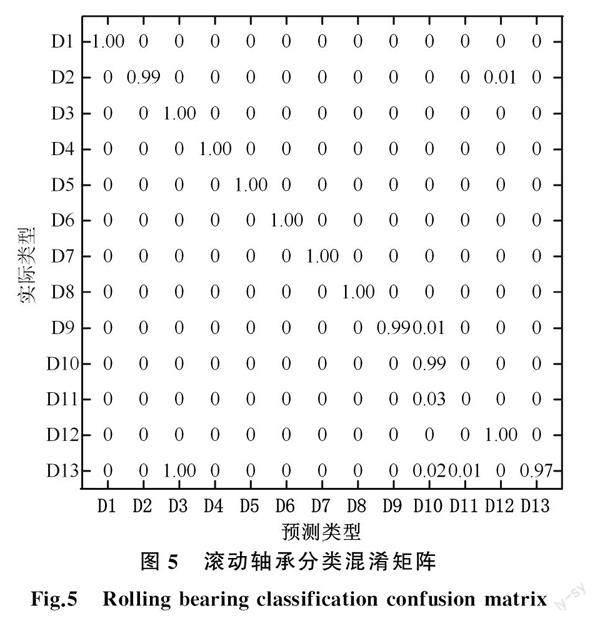
MIF-DTL的分类混淆矩阵（图5）显示，故障诊断的识别准确率超过96%，8类故障的识别准确率达到100%。

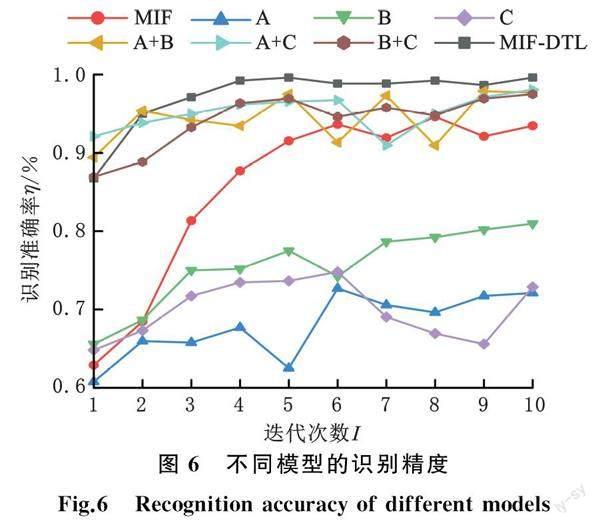
图6所示为不同模型的验证集识别精度训练曲线。MIF-DTL在训练中的测试结果比较一致且识别准确率高于其他方法。与MIF模型比较，MIF-DTL模型的准确性更高、稳定性更好。

使用T-sne对不同模型的输出特征进行降维，绘制可视化图（图7），可以发现MIF-DTL能准确分类故障特征，且每类故障的分布界限明显、类内间距很小，这进一步说明MIF-DTL提取特征效果的更好。

综合上述实验结果可以发现，MIF-DTL能区分不同故障类型的特征，识别准确率高于其他模型，稳定性更高。

3.1.4 不同预训练模型的迁移试验结果与分析

将MIF-DTL与ImageNet上预训练好的深度学习模型AlexNet、VGG16、inceptionV3和DenseNet121进行对比实验。其中，AlexNet是一个5层卷积层的网络，参数较少；VGG16、inceptionV3和DenseNet121模型的卷积层数分别为16、46和121，均属于深层神经网络，具有模型复杂、参数量大的特点。

由表5可以看出，MIF-DTL的平均识别准确率高达99.23%，比其他深度学习模型更优。AlexNet受限于较少的卷积层与模型参数，尽管训练时间最短，但平均准确率为93.54%。VGG16、inceptionV3、DenseNet121的识别准确率分别为81.85%、95.77%和96.12%。MIF模型准确率为94.67%，且训练时间达到最长的445.43 s。由此可见，进行迁移学习的模型拥有更高的训练速度和识别准确率。

综合上述实验结果发现，MIF-DTL使用预训练好的模型参数，降低了模型调参难度，缩短了网络训练时间，能更快地完成模型的训练。

3.2 机车轴承故障诊断（案例2）

在20 kHz的采样频率下，使用三通道（加速度传感器a、b、c）采集机车轴承的振动信号［17］。

3.2.1 数据集的预处理

如表6所示，本试验采集了9种机车轴承故障（编号E1～E9）的数据。对数据进行无重叠分割，每2400个数据点构成一个样本。

3.2.2 MIF-DTL的故障诊断实验结果

由表7可以发现，MIF-DTL方法故障识别准确率的最大值为100%，最小值为99.44%，平均值为99.78%，标准差为0.17%。

3种单传感器的故障诊断模型实验中，故障诊断模型B的表现最好。融合2个传感器的数据信息进行故障诊断的综合效果优于单个传感器，其中，模型传感器a+传感器b识别准确率的最大值为100%，最小值为98.61%，平均值为99.31%，标准差为0.39%，识别准确率和模型的稳定性均低于MIF-DTL。

MIF故障诊断模型识别准确率的最大值为99.16%，最小值为98.05%，平均值为98.67%，标准差为0.34%，识别准确率和模型的稳定性均低于MIF-DTL。

图8为不同模型的T-sne输出特征降维可视化图，对比模型特征分类结果发现，MIF-DTL能准确分类故障特征，每类故障分布界限明显，类内间距很小。

3.2.3 不同预训练模型迁移试验结果与分析

将MIF-DTL与其他4种在ImageNet上训练好的预训练模型进行对比。由表8可以看出，AlexNet、VGG16、inceptionV3、DenseNet121的故障识别率分别为98.67%、87.03%、99.42%和97.11%。AlexNet的卷积层与模型参数较少，模型完全训练好所需的迭代次数较少，且训练时间较短。由于VGG16和DenseNet121的卷积层数多于AlexNet模型，因此参数传递需要更多的迭代。在仅训练10代的情况下，VGG16和DenseNet121的模型还没有完全收敛，所以实验准确率低于AlexNet模型。MIF-DTL的表现最佳，平均准确率为99.78%，模型的训练时间为39.67 s。MIF的准确率为98.67%，训练时间为307.43 s。

综合上述实验结果能够得出，MIF-DTL故障诊断模型在机车轴承数据集中也能实现稳定、精确且快速的故障诊断。

3.3 齿轮故障诊断（案例3）

齿轮箱齿轮数据集［18］来自变速箱输入侧、变速箱输出侧和变速箱安装板上3个单轴加速度计采集的振动信号。

3.3.1 数据集的预处理

如表9所示，试验采集了3个齿轮在10种不同的健康状态下的数据，样本数据长度为1024个数据点，使用无重叠的采样方式进行样本构造。

3.3.2 MIF-DTL的故障诊断试验结果

分析图9的试验结果发现，MIF-DTL的故障识别准确率最高，该方法的最大值为99.75%，最小值为99.0%，平均值为99.5%，标准差为0.25%。

3种单传感器的故障诊断模型实验中，故障诊断模型C的表现最好。融合2个传感器的数据信息故障诊断效果优于单个传感器，其中，故障诊断模型B+C的识别准确率最大值为99.25%，最小值为97.75%，平均值为98.73%，标准差为0.49%，识别准确率和模型的稳定性均低于MIF-DTL。

此外，MIF识别准确率的最大值为95.5%，最小值为92.25%，平均值为93.68%，标准差为0.94%，识别准确率和模型的稳定性均低于MIF-DTL。

由图10可以发现，MIF-DTL能实现准确的故障特征分类，每类故障分布界限明显，类内间距很小，进一步说明MIF-DTL提取的特征效果更好。

综合上述实验结果能够得出结论：MIF-DTL能实现准确的故障特征分类，识别准确率高于其他模型，且能够保持更高的稳定性。

3.3.3 不同迁移模型的试验对比

将MIF-DTL与其他4种ImageNet上训练好的预训练模型进行对比试验。由表10可以看出，AlexNet、VGG16、inceptionV3、DenseNet121的故障识别率分别为90.63%、60.78%、97.15%和90.33%。MIF-DTL的平均準确率为99.5%，模型的训练时间为47.72 s，而MIF的准确率为93.68%，训练时间为339.05 s。

综合上述实验结果能够发现，MIF-DTL在齿轮数据集上也能实现精准且快速的故障诊断。

3.4 不同输入形式下的故障诊断效果对比实验

本节使用案例1、案例2与案例3中的数据集，进行不同输入形式下的故障诊断效果对比实验。对比实验分别为：将一维原始数据输入一维ResNet网络；将224×224的灰度图（特征图）输入已预训练的ResNet网络。不同输入的诊断结果如表11所示。

综合上述实验结果能够发现，MIF-DTL准确率的均值最高。一维原始数据的准确率最低，是由于ResNet擅长图像分类。灰度图生成方式需要更多的数据点，导致样本数量减少。样本不足会降低深度学习网络的训练效果，造成模型过拟合，从而影响了实验准确率。因此，灰度图的准确率低于MIF-DTL。

3.5 不同工况间的小样本迁移实验

本节对凯斯西储大学（CWRU）的轴承数据集进行了跨工况的迁移实验。轴承损伤采用电火花加工，故障深度为0.28 mm，故障直径分别为0.18 mm、0.36 mm、0.54  mm。将样本数据长度设为1024个数据点，采用无重叠采样的方式构造样本。表12显示了数据集的样本构造情况，其中，工况0～3分别表示电机负载为0、746 W、1492 W、2238 W。

在某工况下，迭代10次生成MIF-DTL模型。然后，分别采用直接迁移模型，用1个目标域样本微调MIF-DTL模型参数和用10%的目标域样本微调MIF-DTL模型参数。通过故障诊断实验，分析MIF-DTL在不同工况间的迁移效果。

本文中的迁移任务0→1表示将工况0下生成的MIF-DTL模型（工况0为源域）迁移应用到工况１下的滚动轴承故障诊断中（工况1为目标域）。对于迁移任务中可能存在的12种工况迁移，重复10次实验，识别准确率的平均值如图11所示。

随着负载增大，变刚度振动对应频率的幅值逐渐减小［20］，对于凯斯西储大学的轴承数据集，负载增大时，滚动轴承振动信号的频率幅值也逐渐减小。缺陷尺寸越小，轴承振动信号受负载影响的程度越大［21］，因此，负载的增大会加速轴承故障尺寸的扩展。由图11所示的实验结果能发现，迁移任务0→1、1→0、1→2、2→1、2→3、3→2等工况相近的情况下，直接迁移模型的识别准确率均在95%以上；其他的迁移任务中，MIF-DTL模型均展现了较高的识别准确率，仅在迁移任务3→0中的识别准确率低于80%。这可能是因为模型在工况3（源域）学习的是高负载下的低幅值特征，而滚动轴承在工况0（目标域）时表现出高幅值特征，两类特征区别过大，导致迁移任务3→0的识别效果不佳。

使用1个目标域样本作为MIF-DTL训练集进行模型参数微调，能提高MIF-DTL模型不同工况间小样本迁移的识别准确率。采用10%的目标域样本作为MIF-DTL训练集进行模型参数微调，迁移后的识别准确率均超过97.5%，迁移任务1→0、1→2、1→3、2→1、2→3的识别准确率接近99%，这验证了MIF-DTL模型在工况迁移任务下的有效性。

4 结论

（1）利用小波变换对多个传感器信号进行时频分析，时频图与多通道信息融合得到的RGB图像数据不仅能够充分挖掘故障数据，且可以最大程度发挥深度学习网络对图像数据特征提取的性能。

（2）实验室和真实机车轴承数据集的试验结果证明，MIF-DTL能够有效诊断故障，并具有训练快、泛化强和识别精确等优点。

（3）直接迁移模型和目标域样本微调模型试验验证了MIF-DTL模型在不同工况间的小样本迁移的有效性。

参考文献：

［1］张龙， 甄灿壮， 易剑昱， 等. 双通道特征融合CNN-GRU齿轮箱故障诊断［J］. 振动与冲击， 2021， 40（19）：239-245.

ZHANG Long， ZHEN Canzhuang， YI Jianyu， et al. Dual-channel Feature Fusion CNN-GRU Gearbox Fault Diagnosis［J］. Journal of Vibration and Shock， 2021， 40（19）：239-245.

［2］周奇才， 刘星辰， 赵炯， 等. 旋转机械一维深度卷积神经网络故障诊断研究［J］. 振动与冲击， 2018， 37（23）：31-37.

ZHOU Qicai， LIU Xingchen， ZHAO Jiong， et al. Fault Diagnosis for Rotating Machinery Based on 1D Depth Convolutional Neural Network［J］. Journal of Vibration and Shock， 2018， 37（23）：39-45.

［2］CHEN S， GE H， LI H， et al. Hierarchical Deep Convolution Neural Networks Based on Transfer Learning for Transformer Rectifier Unit Fault Diagnosis［J］. Measurement， 2021， 167：108257.

［4］LI F， TANG T， TANG B， et al. Deep Convolution Domain-adversarial Transfer Learning for Fault Diagnosis of Rolling Bearings［J］. Measurement， 2021， 169：108339.

［5］QIAN C， ZHU J， SHEN Y， et al. Deep Transfer Learning in Mechanical Intelligent Fault Diagnosis：Application and Challenge［J］. Neural Processing Letters， 2022， 54（3）：2509-2531.

［6］SEGEV N， HAREL M， MANNOR S， et al. Learn on Source， Refine on Target：a Model Transfer Learning Framework with Random Forests［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2016， 39（9）：1811-1824.

［7］ZHANG R， TAO H， WU L， et al. Transfer Learning with Neural Networks for Bearing Fault Diagnosis in Changing Working Conditions［J］. IEEE Access， 2017， 5：14347-14357.

［8］陳仁祥， 杨星， 胡小林， 等. 深度置信网络迁移学习的行星齿轮箱故障诊断方法［J］. 振动与冲击， 2021， 40（1）：127-133.

CHEN Renxiang， YANG Xing， HU Xiaolin， et al. Planetary Gearbox Fault Diagnosis Method Based on Deep Belief Network Transfer Learning［J］. Journal of Vibration and Shock， 2021， 40（1）：127-133.

［9］SHAO S， MCALEER S， YAN R， et al. Highly Accurate Machine Fault Diagnosis Using Deep Transfer Learning［J］. IEEE Transactions on Industrial Informatics， 2019， 15（4）：2446-2455.

［10］刘飞， 陈仁文， 邢凯玲， 等. 基于迁移学习与深度残差网络的滚动轴承快速故障诊断算法［J］. 振动与冲击， 2022， 41（3）：154-164.

LIU Fei， CHEN Renwen， XING Kailing， et al. Fast Fault Diagnosis Algorithm for Rolling Bearing Based on Transfer Learning and Deep Residual Network［J］. Journal of Vibration and Shock， 2022， 41（3）：154-164.

［11］SHE D， JIA M. Wear Indicator Construction of Rolling  Bearings Based on Multi-channel Deep Convolutional Neural Network with Exponentially Decaying Learning Rate［J］. Measurement， 2019， 135：368-375.

［12］CHE C， WANG H， NI X， et al. Domain Adaptive Deep Belief Network for Rolling Bearing Fault Diagnosis［J］. Computers & Industrial Engineering， 2020， 143：106427.

［13］SOUZA R M， NASCIMENTO E G S， MIRANDA U A， et al. Deep Learning for Diagnosis and Classification of Faults in Industrial Rotating Machinery［J］. Computers & Industrial Engineering， 2021， 153：107060.

［14］PAN S J， YANG Q. A Survey on Transfer Learning［J］. IEEE Transactions on Knowledge and Data Engineering， 2009， 22（10）：1345-1359.

［15］GE W， YU Y. Borrowing Treasures from the Wealthy：Deep Transfer Learning through Selective Joint Fine-tuning［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2018， 40（8）：1924-1937

［16］KUMAR A， ZHOU Y， GANDHI C P， et al. Bearing Defect Size Assessment Using Wavelet Transform Based Deep Convolutional Neural Network（DCNN）［J］. Alexandria Engineering Journal， 2020， 59（2）：999-1012.

［17］張龙， 甄灿壮， 熊国良， 等. 基于深度时频特征的机车轴承故障诊断［J］. 交通运输工程学报， 2021， 21（6）：247-258.

ZHANG Long， ZHEN Canzhuang， XIONG Guoliang， et al. Locomotive Bearing Fault Diagnosis Based on Deep Time-frequency Features［J］. Journal of Traffic and Transportation Engineering， 2021， 21（6）：247-258.

［18］HE J， YANG S， PAPATHEOU E， et al. Investigation of a Multi-sensor Data Fusion Technique for the Fault Diagnosis of Gearboxes［J］. Proceedings of the Institution of Mechanical Engineers， Part C：Journal of Mechanical Engineering Science， 2019， 233（13）：4764-4775.

［19］徐敬领， 霍家庆， 宋连腾， 等. 基于测井数据的米氏旋回分析及浮动天文年代标尺的建立［J］. 地球物理学报， 2022， 65（7）：2766-2778.

XU Jingling， HUO Jiaqing， SONG Lianteng， et al. Analysis of Milankovitch Cycles and Establishment of Floating Astronomical Date Scale Based on Well-logging Data［J］. Chinese Journal of Geophysics， 2022， 65（7）：2766-2778.

［20］唐云冰， 高德平， 罗贵火. 滚动轴承非线性轴承力及其对轴承系统振动特性的影响［J］. 航空动力学报， 2006， 21（2）：366-373.

TANG Yunbing， GAO Deping， LUO Guihuo. Nonlinear Bearing Force of the Rolling Ball Bearing and Its Influence on Vibration of Bearing System［J］. Journal of Aerospace Power， 2006， 21（2）：366-373.

［21］刘畅. 非稳态条件下滚动轴承故障诊断及退化识别技术研究［D］. 徐州：中国矿业大学， 2021.

LIU Chang. Study on Fault Diagnosis and Degradation Identification Technology of Rolling Bearing under Unsteady Condition［D］. Xuzhou：China University of Mining and Technology， 2021.

（编辑 张 洋）

作者简介：

张 龙，男，1980年生，教授。研究方向为机电和轨道交通装备状态监测与故障诊断。E-mail：longzh@126.com。

收稿日期：2022-05-31

基金项目：国家自然科学基金（51665013）；江西省自然科学基金 （20212BAB204007）；江西省研究生创新资金 （YC2020-S335，YC2021-S42）。