整体叶盘叶片型面高精度六轴检测与误差补偿方法研究

郑刚　闫立方　张开伟　张旭

摘要：为提高三坐标测量机对整体叶盘的测量效率和精度，解决大尺寸整体叶盘超出测量机量程等问题，构建了基于三坐标测量机和高精度转台的六轴测量系统。依据空间坐标变换原理建立了转台坐标系与叶盘工件坐标系的数学模型，提出了一种整体叶盘不同叶片坐标系随转台旋转后的空间误差补偿方法。检测结果表明，在保证每个叶片型面参数测量精度满足工艺要求的前提下，测量效率平均提高了28.22%。对比未配置转台的测量数据，新的六轴测量系统测量水平整体叶盘叶片型面轮廓对比误差基本在0.008 mm以内，最大对比误差小于0.015 mm，比测量倾斜整体叶盘的误差更小且更稳定。

关键词：三坐标测量机；整体叶盘；转台；六轴系统；误差补偿

中图分类号：V263

DOI：10.3969/j.issn.1004-132X.2023.08.004

Research on High-precision Six-axis Detection and Error CompensationMethod for Blisk Blade Profiles

ZHENG Gang YAN Lifang ZHANG Kaiwei ZHANG Xu

Abstract： In order to improve the measurement efficiency and accuracy of the overall blisk by CMM and to solve the problems that large-sized blisk exceeded the measuring range of measuring machine， a six-axis measurement system was constructed based on CMM and a high-precision turntable. According to the principle of space coordinate transformation， a mathematical model of the turntable coordinate system and the blisk workpiece coordinate system were established. A space error compensation method was proposed after the coordinate systems of different blades of the blisk rotated with the turntable. Test results show that the measurement efficiency increases by 28.22% on average under the premise of ensuring that the measurement accuracy of each blade profile parameter meets the process requirements. Compared with the measurement data without the turntable， the new six-axis measurement system measures the horizontal blisk blade profile， and the profile comparison errors are almost all within 0.008 mm. The maximum comparison error is less than 0.015 mm， which is smaller and more stable than the measurement errors of the inclined blisk.

Key words： coordinate measuring machine（CMM）； blisk； turntable； six-axis system； error compensation

0 引言

整體叶盘广泛应用于航空、国防、能源等行业， 其叶片型面曲线、叶身表面粗糙度、前后缘曲率半径和形状特性在很大程度上决定了工作环境中介质的能量转换率，影响着相关产品的性能和寿命，因此，高精度检测对型面尺寸的控制成为了整体叶盘制造的关键环节，对保证和提升整体叶盘的质量有重要意义［1-2］。

整体叶盘叶片型面的检测主要是对叶片前缘、后缘、叶盆、叶背的轮廓和叶型厚度、叶片弦长等关键尺寸的检测［3］。传统的叶片检测主要以人工为主，操作简单，适宜现场生产，但精度低，只能对叶片型面进行定性分析，并不能获取精确的测量误差［4-5］。新的叶片型面检测方法基本分为非接触式测量和接触式测量两类。非接触测量是基于立体视差原理获得三维数据，解算几何信息，具有实时性、高效率、易达性等优点，十分适用于开放式单叶片的测量，但对于整体叶盘这种自由曲面复杂、扭曲度大、流道狭窄的工件，很难完成叶片型面的检测［6-7］。虽然蔡司GOM ATOS 5 Aifoil蓝光扫描仪可以实现整体叶盘的三维快速扫描，但其工作距离较短，只适合小面积范围叶片的测量，具有一定局限性。三坐标测量机（coordinate measuring machine， CMM）的出现为整体叶盘叶片型面的接触测量提供了有效的技术手段。它主要通过测量头与叶片轮廓逐点接触采集点集坐标，通过迭代配准算法配准模型，对比、分析实际与理论的叶片型面参数误差，具有精度高、重复性高、通用性强等特点［8］，主要问题是效率低。如何利用CMM高效且无干涉地测量整体叶盘成为研究的重点。

目前，CMM对整体叶盘测量主要有两种技术路径：一是采用配置精密转台的高精度CMM实现四轴联动；二是采用配置多轴测座及高精度扫描测头进行测量。海克斯康公司配置了Quindos软件和高精度转台，开发了一款Leitz超高精度测量专机，实现了叶盘高精度、高效率的测量［9］。蔡司四轴联动转台RB-RB 100技术也实现了单式叶片的联动测量，但却不易于整体叶盘封闭类零件的检测。Renishaw公司实现了五轴连续扫描技术与自动扫描路径规划系统的创新，推出具备五轴测量能力的动态测量系统［10-11］，其Revo五轴测座突破了传统坐标测量机的三轴测座，完成了两个旋转轴上同步运动，极大提高了测量效率。在测量机上搭配APEX Blade软件，可以针对被测整体叶盘自动生成最佳扫描路径，合理进行避让［12］。在实际测量过程中，上述两种技术方式各有优势与不足：①海克斯康公司研发的Leitz测量专机，配置了第四轴精密转台和多角度的触发式测头，极大提高了测量效率，但测头角度固定，只能测量形状参数差别较小的整体叶盘，通用性不高，性价比较低［13］；②配置Revo测座的坐标测量机灵活性较强，基本可以满足大部分类型与尺寸的整体叶盘测量，相对于四轴联动技术而言适用性更强；③Revo测量机并未配置高精度转台，通过高自由度动态测量系统可完成整个叶盘的测量，但对于较大尺寸的叶盘存在超出测量机量程而无法测量的情况，因此精度难以保证，成本更高；④Revo坐标测量机在实现某一叶片到下一叶片的测量中存在大量的安全点，大大降低了对整体叶盘的测量效率。

可见，四轴联动技术和五轴测量机整体叶盘检测各有优劣势。在CMM上增加第六轴转台可以简化测量过程、提高效率，但会引入新的误差，因此需要解决坐标轴的校准和误差的补偿问题。HUANG等［14-15］对机床旋转轴的兩种常用的几何误差定义特征和关系进行了分析，利用获取的点集坐标逆向校准旋转轴的几何误差。LIU等［16］以构造等效旋转轴的方式，使用6个参数描述和补偿五轴机床中旋转轴的几何误差。WANG等［17］通过构建探针坐标系与工件坐标系之间的变换关系，提出了一种新的校准方法来补偿探针的安装误差，但并未关注转台与工件之间的关系。ZHANG等［18］在理想状态下，通过优化转台的旋转角度和探头倾角的变化来避免测量中干涉，实现了CMM扫描叶片路径的自动规划，但对实际测量过程中的各项误差缺乏考虑。徐永安等［19］测量转台旋转不同角度下的标准球心坐标，通过几何变换对转台转台中心轴线进行了修正。潘金川等［20］对整体叶轮中心轴与分度装置的中心轴不重合产生的运动偏心给出补偿方法，但只对测量的数据点进行了补偿，补偿方式计算量大、效率低。目前，对转台自身的几何误差和补偿已被充分研究，但对测量过程中工件与转台相对关系的研究较少，解决此类问题的方案也很少应用于配置转台CMM对整体叶盘的测量，因此，需要关注CMM在配置转台后，工件随转台旋转变化而产生的实际测量误差。

为实现配置转台CMM对整体叶盘的高精度检测，本文对三坐标测量系统进行转台的配置与标定，解决回转一定角度值的转台坐标系与零件坐标系之间的空间误差问题，避免旋转转台后需要重复以基准特征建立测量坐标系的复杂过程，并对误差进行精确补偿。最后进行了实验验证。

1 转台配置

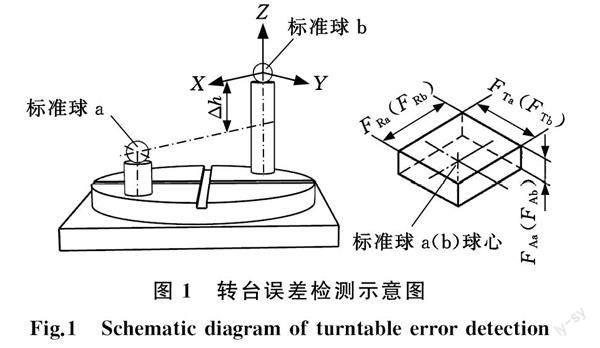
当坐标测量机配置转台时，转台的回转运动和精度偏差会影响整体的坐标测量结果，因此，首先需要评价带有直流有刷伺服电机驱动气浮转台的坐标测量的精度。在配置Revo测座高精度五轴坐标测量机测量环境下，根据国家标准GBT 16857.3—2009标准要求，将两个标准球安装固定在气浮转台上，如图1所示，a球为高球，b球为低球，两球球度误差小于1 μm，高度差为Δh，在不同角度下测量两个球的球心坐标，建立两个球的球心坐标系，分别旋转不同的角度反复测量，计算a与b球的各向误差：径向误差FRa和FRb、切向误差FTa和FTb、轴向误差FAa和FAb。

检测的转台最大各向误差满足被测零件的精度是作为坐标测量机第六运动轴的必要条件。五轴坐标测量机一般通过控制器与放大器对各轴驱动，直流有刷伺服电机驱动的第六轴气浮转台需要一个专用的放大器进行相应的运动。整个配置过程包括硬件连接、UCC软件配置和转台参数调节三个部分。如图2所示，放大器SPA3作为UCC控制气浮转台运动的中转，硬件连接完成后，再对UCC软件系统进行匹配，并调节转台的电流环、速度环、位置环参数，若UCC控制器实现软硬件控制转台成功回零，则配置完成。

转台配置完成后需进行标定，其过程是确定实际转台坐标系在机床坐标系下的位置与姿态。根据转台平面法向确定Z轴矢量及高度，根据固定于转台上的标准球随转台旋转一周后的球心拟合圆确定X、Y轴原点。此时UCC控制系统可以确定转台坐标系精确位置Pb与Z轴矢量，产生交互界面并形成六轴测量系统。

2 误差分析

三坐标测量机配置了气浮转台后，整体叶盘圆周阵列测量指令可以通过气浮回转运动实现，即第i（i=1，2，3...）个叶片测量完毕后，要测量第i+1个叶片时，只需要回转台回转一个角度值，即可在新的叶片上测量。但在实际的测量过程中，叶盘坐标系的回转轴与气浮转台的回转轴线不能保持完全一致，回转运动会带来叶片坐标系的位置变动。同时，整体叶盘相对于转台相对位置不同也会引入误差，两者相对位置主要包括整体叶盘精建坐标系相对转台坐标系平行和整体叶盘精建坐标系相对转台坐标系倾斜。

当转台坐标系X-Y平面与整体叶盘坐标系任意轴线构成的平面近似平行时，整体叶盘坐标系旋转前后点位误差可以转化为在机床坐标系X-Y平面投影上的二维误差，如图3a所示，整体叶盘随转台逆时针旋转θ后，旋转前叶盘0°位置叶片坐标系与旋转后叶盘θ位置叶片坐标系下的点位存在误差，且随着旋转角度的增大而增大。推广到三维，同样当转台坐标系X-Y平面与整体叶盘坐标系任意轴线构成的平面存在一定夹角时，如图3b所示，三维点位空间误差更显著。因此消除转台引入的测量误差是完成精确检测的关键。又由于叶片曲面不同点位的误差值各异，当没有通用的补偿方式时，会增大补偿工作量，降低测量效率，

为此将点位的误差补偿转化为坐标系空间位置与姿态误差补偿。

3 误差补偿

3.1 矢量轴线计算

对前后叶片坐标系补偿值的计算，实际是确定叶盘坐标系{C}旋转前后相对于机床坐标系{A}与转台坐标系{B}的位置与姿态变换关系。在转台标定与精建坐标系后，可以得到{C}、{B}与{A}之间的精确相对位置。用XACi、YACi和ZACi表示第i片叶片坐标系{Ci}相对于坐标系{A}的主轴单位矢量。用XAB、YAB和ZAB表示{B}相对于{A}的主轴单位矢量。叶盘坐标系绕转台坐标系中心轴线旋转，当选择{B}主轴中一个轴作为旋转轴时，坐标系{C}变化的等效旋转矩阵为

其中，arctan2（y，x）是双参变量的反正切函数，欧拉角将在以下范围：-π<α<π、-π/2<β<π/2、-π<γ<π。求出坐标系{C1}到{Ci}旋转Z-Y-X欧拉角及偏移量后，将其输入控制程序中，即可完成整体叶盘坐标系随转台旋转产生的误差补偿。

4 实验

4.1 对象及目标

对已经研发的整体叶盘的叶片型面进行检测，该工件包含上下两级叶盘，上级共21片叶片，下级为23片叶片。零件三维模型如图5a所示，坐标系以上基准平面B、基准孔A及叶片型面角相点确定。叶片型面参数最小形位公差为0.08 mm，其决定几何形状精度的关键参数有叶型轮廓度、积叠点位置度、弦长和叶型最大厚度，如图5b所示。

实验会抽取上级叶盘圆周5片叶片进行测量，测量第1个叶片后，逆时针旋转转台，测量第3、7、13、17个叶片。同时为充分验证文中测量系统与方法的精度与效率，在环境条件不变的情况下考虑了3组测量，包括：使用未配置气浮轉台CMM测量整体叶盘叶片型面；使用配置气浮转台CMM测量水平放置整体叶盘叶片型面；使用配置气浮转台CMM测量倾斜放置整体叶盘叶片型面。同时，分析对比3组叶片测量数据及消耗时间，判断各组精度与效率情况。

4.2 实验平台

该系统基于Wenzel LH1210-2000五轴坐标测量机，搭配Renishaw Revo测座，测针红宝石直径2 mm，测杆长30 mm，整体精度可达2.6+L/350 μm。按照第1节转台配置与标定要求，采用SPA3放大器实现UCC S5控制器对直流有刷伺服电机驱动的气浮转台进行驱动，六轴系统调试成功后，气浮转台的运动可以通过Modus程序控制，也可以利用手柄控制器调节。软件方面配置了Modus1.9版本和APEX Blade叶片型面测量路径规划软件，同时采用MATLAB编制算法并计算测量坐标系之间的补偿值。最后通过简易的固定装置将整体叶盘紧固在气浮转台上。完整检测平台如图6所示。

4.3 实验准备

按照第1节所述配置转台轴线为第六轴的坐标测量机误差检测方法，对气浮转台精度等级进行评定，各项误差结果如表1所示。

由表1可知，转台各项误差值最大为0.0077 mm，因被测整体叶盘的最紧公差带为0.08 mm，转台各项最大误差小于1/10最紧公差，可以判定气浮转台作为测量机的第六轴可用于该整体叶盘的测量中，精度等级为一般。

4.4 实验过程

整体叶盘测量程序在Modus1.9上进行，通过选取模型平面和孔特征，确定整体叶盘的回转轴线和X-Y平面，在第1个叶片测量一点，建立零点的粗基准，以叶片上测量多点使用迭代的方法建立零点的精基准。当转台坐标系与整体叶盘第1个叶片精建坐标系确定后，根据第3节所述补偿值算法，可以精确计算第i个叶片坐标系相对于第1个叶片坐标系之间的补偿值。不配置转台测量整体叶盘为第1组实验，整体叶盘水平紧固于转台的测量为第2组实验，整体叶盘倾斜紧固于转台的测量为第3组实验，则2、3组测量补偿值如表2所示。

坐标系建立完成后编制第1个叶片型面测量程序，程序编制可分为手动构造截面生成程序和利用专用软件生成摆扫程序两种方式。软件自动生成摆扫程序时可以设置测头的速度、加速度和搜寻距离等参数，计算机可以自动规避干涉点生成最佳扫描路径，比手动构造截面效率更高。采用APEX Blade软件生成叶片型面扫描程序，软件Modus1.9运行扫描程序。测针完成扫描后对各个截面进行评价，扫描过程如图7所示。

在进行第i个叶片测量时，叶片的测量程序保持一致，整体叶盘的分析评价程序保持一致，只是在圆周阵列测量程序上不同。转台只需回转一定角度，将表2中对应补偿值输入控制程序（图8），控制转台旋转相应角度，对旋转前的坐标系依次进行平移与旋转变换，最终得到第i个叶片坐标系，而后，Revo测座在原有朝向和几乎原位置下进行叶片测量。测量完成后对比3组实验整体叶盘叶片型面的测量精度与耗时，分析效率及精度变化情况。

5 结果分析

5.1 精度分析

分别取第1、2、3组各5个叶片截面高度为77 mm型面实测参数值进行分析。各组叶片型面参数测量数据如图9所示，叶片轮廓度、最大厚度、弦长和位置度均满足图5b中公差要求。第2、3组测量数据与第1组测量数据的对比误差如图10所示。图9与图10中横坐标表示不同含义，如1-1表示第1组实验的1号叶片；2-1-1表示第2组实验与第1组实验中的1号叶片进行对比。

从图10中可以看出，第2、3组测量的叶片型面整体轮廓度公差带相对于第1组结果误差在0.008 mm以内。但1号叶片的前缘轮廓度公差带误差最大达到0.015 mm，倾斜放置整体叶盘与水平放置整体叶盘的叶片轮廓度测量误差影响都相对较小。叶片型面最大厚度与弦长测量呈现较高的一致性，对比误差小于0.05 mm。叶片型面积叠点位置度的误差会随旋转角度的增大而增大，最大对比误差为0.15 mm。同时，水平放置整体叶盘测量时叶片型面积叠点位置变化较小，而倾斜放置整体叶盘时叶片型面积叠点位置受旋转角度的影响较大。由于CMM系统误差与气浮转台误差的影响，倾斜放置整体叶盘叶片型面的测量累积误差较大，若后续将转台旋转分度误差补偿写入控制器，则可以进一步提高该六轴系统对整体叶盘的测量精度。

5.2 效率分析

叶盘每一个角度叶片的测量时间是由编制的叶片程序与测量机的运行时间决定的。当设置一定参数后，每个叶片的摆扫时间是确定的，测量时间为289 s。无转台测量与有转台测量时叶片的摆扫消耗时间是一致且确定的，有转台测量相对于无转台测量节省的时间是测量机前后走安全点消耗的时间。测量每片叶片节省的时间，并计算节省时间与每个叶片测量总时间的比值。结果显示每个叶片测量效率平均提高28.22%，详细数据如表3 所示。

5.3 尺寸分析

为充分验证该六轴测量系统与补偿方法的通用性，在气浮转台上紧固了直径约550 mm的整体叶盘，连续对超出坐标测量机量程部分的叶片进行测量。由于测量机的量程有限，故在未配置转台情况下不能移动到转台180°叶片的位置进行测量；配置转台后可以充分利用转台的旋转，将180°位置叶片旋转到测量机量程范围内的0°叶片位置，结合上述补偿理论，可以实现180°位置叶片的测量。实际上，该六轴测量系统与补偿方法只需满足测量整体叶盘其中某一片叶片条件就可以实现该整体叶盘圆周所有叶片的测量，具有较强的适用性。

6 结论

（1）本研究实现了配置转台三坐标六轴测量系统对整体叶盘叶片型面的新检测方法，利用机器人学空间坐标变换原理建立数学模型，针对回转一定角度值的转台坐标系与整体叶盘坐标系之间的空间误差问题，给出了精确的误差补偿，解决了配置转台测量整体叶盘过程中需要重复以基准特征建立测量坐标系的问题，提高了测量效率。

（2）六轴检测系统可以满足最紧公差带为0.08 mm的整体叶盘叶片型面的检测要求，每个叶片型面参数测量精度满足工艺要求，且相较于未配置转台系统测量效率平均提高了28.22%，水平放置整体叶盘的测量误差比倾斜放置整体叶盘的测量误差更小且更稳定。

（3）本研究在五轴测量机上配置六轴系统的方法和空间补偿算法都具有一定通用性，可为一些大尺寸的整体叶盘存在超出测量机导程而无法测量的问题提供解决方法。

参考文献：

［1］陆佳艳，熊昌友，何小妹，等.航空发动机叶片型面测量方法评述［J］.计测技术，2009，29（3）：1-3.

LU Jiayan， XIONG Changyou， HE Xiaomei， et al. Survey of Measurement Method of Aero-engine Blade［J］. Metrology & Measurement Technology， 2009，29（3）：1-3.

［2］张国雄. 三坐标测量机的发展趋势［J］. 中国机械工程，2000（增刊1）：231-235.

ZHANG Guoxiong. Automatic Inspection Feature Extraction and Recognition in CMM Inspection Planning［J］. China Mechanical Engineering，2000（S1）：231-235.

［3］YU Jianhua， CHEN Zhitong， JIANG Zepeng. An Approach for Machining Distortion Measurements and Evaluation of Thin-walled Blades with Small Datum［J］.Chinese Journal of Aeronautics， 2016，29（6）：1806-1814.

［4］SAVIO E， DE CHIFFRE L， SCHMITT R. Metrology of Freeform Shaped Parts［J］. CIRP Annals， 2007， 56（2）：810-835.

［5］BOOTH M C， RIDDELL S G， WILSON M M. Template for Aligning Surface Features on a Rotor Blade：US 9624782［P］. 2017-04-18.

［6］GAO Y， LIN X， SHI Y， et al. Accessibility Analysis in Efficient Inspection of Closed Blisk on 3-axis CMM with 2-axis Probe Head［J］. Precision Engineering， 2019， 57：104-112.

［7］李學哲，石照耀，陈洪芳， 等.航空发动机叶片型面测量技术研究现状与趋势［J］.北京工业大学学报，2017，43（4）：557-565.

LI Xuezhe， SHI Zhaoyao， CHEN Hongfang， et al. Current Status and Trends of Aerogengine Blade Profile Metrology［J］. Journal of Beijing University of Technology， 2017， 43（4）：557-565.

［8］蔺小军， 吴刚， 单秀峰， 等. 基于叶片截面线CMM测量数据的ICP配准改进算法［J］. 机械工程学报， 2020， 56（2）：1-8.

LIN Xiaojun， WU Gang， SHAN Xiufeng， et al. An Improved ICP Registration Algorithm Based on CMM Measurement Data of Blade Section Line［J］. Journal of Mechanical Engineering， 2020， 56（2）：1-8.

［9］孟书广.航空发动机复杂零部件的新型测量技术［J］.航空制造技术，2014（13）：32-35.

MENG Shuguang. New Metrology Technique for Complex Components of Aero-engine［J］. Aeronautical Manufacturing Technology， 2014（13）：32-35.

［10］ZHOU A， GUO J， SHAO W. Automated Inspection Planning of Freeform Surfaces for Manufacturing Applications［C］∥2011 IEEE International Conference on Mechatronics and Automation. Beijing， 2011：2264-2269.

［11］SOUSA A R. Metrological Evaluation of a Coordinate Measuring Machine with 5-axis Measurement Technology［J］. Procedia CIRP， 2018， 75：367-372.

［12］ZHOU Z， ZHANG Y， TANG K. Sweep Scan Path Planning for Efficient Freeform Surface Inspection on Five-axis CMM［J］. Computer-Aided Design， 2016， 77：1-17.

［13］赵燎. 基于CMM的整体叶盘测量系统研究［D］. 成都：电子科技大学，2020.

ZHAO Liao. Research on CMM-based Measuring System of Blisk［D］. Chengdu：University of Electronic Science and Technology of China， 2020.

［14］HUANG N， BI Q， WANG Y. Identification of Two Different Geometric Error Definitions for the Rotary Axis of the 5-axis Machine Tools［J］. International Journal of Machine Tools and Manufacture， 2015， 91：109-114.

［15］HUANG N， ZHANG S， BI Q， et al. Identification of Geometric Errors of Rotary Axes on 5-axis Machine Tools by On-machine Measurement［J］. The International Journal of Advanced Manufacturing Technology， 2016， 84（1）：505-512.

［16］LIU Y， WAN M， XIAO Q B， et al. Identification and Compensation of Geometric Errors of Rotary Axes in Five-axis Machine Tools through Constructing Equivalent Rotary Axis（ERA）［J］. International Journal of Mechanical Sciences， 2019， 152：211-227.

［17］WANG Z， ZHANG X， SHEN Y， et al. Pose Calibration of Line Structured Light Probe Based on Ball Bar Target in Cylindrical Coordinate Measuring Machines［J］. Measurement， 2021， 171：108760.

［18］ZHANG Y， SHEN Y， ZHANG W， et al. Generation of Efficient and Interference-free Scanning Path for Inspecting Impeller on a Cylindrical CMM［J］. Measurement， 2022，198：111352.

［19］徐永安，楊钦，怀进鹏.转台中心轴线标定误差分析与修正［J］.北京航空航天大学学报，2005（8）：899-903.

XU Yongan， YANG Qin， HUAI Jinpeng. Analysis and Modification of Turntables Axis Calibration［J］. Journal of Beijing University of Aeronautics and Astronautics， 2005（8）：899-903.

［20］潘金川， 刘胜兰， 张丽艳， 等.整体叶轮在分度装置装夹下的CMM测量方法研究［J］. 机械科学与技术， 2015， 34（9）：1388-1393.

PAN Jinchuan， LIU Shenglan， ZHANG Liyan， et al. Research on Measuring Method of Monolithic Impeller with Dividing Apparatusvia CMM［J］. Mechanical Science and Technology for Aerospace Engineering， 2015， 34（9）：1388-1393.

（编辑 王旻玥）

作者简介：

郑 刚，男，1982年生，博士研究生。研究方向为曲面测量与数控加工技术。获发明专利10余项，发表论文20余篇。E-mail：zhenggang@sit.edu.cn。

张 旭（通信作者），男，1982年生，教授。研究方向为曲面测量。E-mail：zhangxu@hust-wuxi.com。

收稿日期：2022-05-03

基金项目：国家重点研发计划（2018YFB1306802）