水下超表面角反射体声散射调控机理研究

刘妍, 彭子龙*, 杜佳曼, 孔慧敏, 范军

(1.江苏科技大学 能源与动力学院, 江苏 镇江 212100; 2.上海交通大学 船舶海洋与建筑工程学院, 上海 200240)

0 引言

声诱饵是当前世界上普遍使用的一种软性武器,在鱼雷干扰、诱骗、水雷诱导等领域得到广泛应用。声诱饵按照其工作模式可分为有源声诱饵和无源声诱饵[1],根据制动方式的不同,声诱饵可分为悬浮式声诱饵、拖曳式声诱饵和自航式声诱饵[2]。当前在水下作战中,诱骗主动声呐探测主要通过模拟仿真舰船目标的声反射强度和尺度特征,一般采用接收响应模式[3]。该方法技术复杂、成本高、实时性差,且容易被有源声呐识别。由于无源声诱饵反应速度快、不易暴露、质量轻、造价低、机动灵活等特点,已成为当前探索和开发的一种新型的技术[4]。角反射器作为一种强回波装置,常用于雷达对抗领域[5],通过特殊的几何结构和材料设计,散射与真目标相似的假信号,以欺骗或诱惑敌方的探测系统或制导系统,在实际作战中通常用来构成假目标或诱饵,具有适应性强、反应时间短、有效干扰时间长、攻防兼备等一系列优点。例如英国DLF-1橡胶舷外充气八面角反射器,以色列宽频攻击雷达诱饵Wizard[6]。针对舰艇等目标的水下声目标特征,利用水下角反射器进行无源模拟作为对抗有源声呐新的方法。对水下角反射器进行声散射特性的研究,提高其反声性能是十分必要的[7-8]。

与传统斯奈尔定律不同,广义斯奈尔定律提出了一个由折射或者反射的界面发生的相位变化[9]。一般采用共振元件来完成相移的转换,借此对表面上的相位突变进行调整,可以完成不同的声散射主方向控制。这种具有亚波长宽度的人造结构叫做超表面。有学者2013年首次提出类似于光学超表面的声场理论设计[10-11],该方法采用一种基于相位突变的结构,使入射波在反射和折射的交界面上符合广义斯奈尔定律,从而形成了一种特异的折射和反射。Christensen等[12]建立了凹槽结构并利用声表面波的耦合实现声场调控。自此基于声学超表面的声波调控能力受到广泛关注。

基于广义斯奈尔定律,本文提出一种镶嵌具有一维深度梯度变化凹槽的二面角反射体,该声学结构可通过调整凹槽深度变化梯度和凹槽深度尺寸实现对散射声场及声散射主方向调控,为水下无源声诱饵的设计研究提供了方向和借鉴。

1 超表面结构的近似算法

与传统斯奈尔定律不同,广义斯奈尔定律中首先提出了表面相位梯度对声波的调控作用,如式(1)所示:

(1)

式中:θr和θi分别为反射角与入射角;λ0为波长;dΦ(x)/dx为表面相位变化梯度。为此,本文提出将角反射体结构表面设计成声学超表面,实现角反射体散射声场的空间调控[13]。为实现声波在表面的相位变化,在均匀表面上构造一组深度随位置梯度变化的凹槽,如图1所示,为实现反射波的相位突变,声学超表面的宽度通常比波长更小[14]。图1中,Oxyz为超表面三维直角坐标系,a为一维超表面宽度,i为被入射声波入射的凹槽序号,d为两个相邻凹槽中心距离,d0为凹槽之间分割区域宽度,hi为第i个凹槽的深度,Q为声源位置,M(xQ,a/2,zQ)为接收点位置(收发合置),xQ为声源或接收点位置所对应的x轴坐标,zQ为声源或接收点位置所对应的z轴坐标,N为超表面的凹槽数量,R为坐标原点O到入射波与超表面交点的矢量,φi、φr为入射波与反射波对应的势函数。

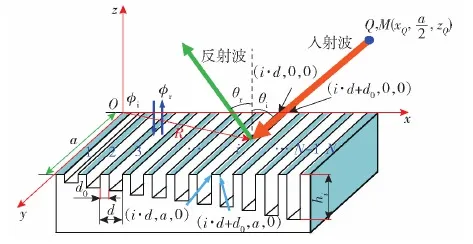
图1 一维超表面散射声场计算模型示意图Fig.1 Schematic diagram of one-dimensional metasurface scattering sound field computation model

1.1 基于板块元的一维声学超表面散射声场求解

板块元计算方法主要利用Kirchhoff近似原理,也称为物理声学法[15]。该方法主要基于以下两个基本假设:

假设1散射表面可以分成产生声波散射的被照亮区域,即亮区,以及不产生声波散射的未被照亮区域,即影区。

假设2亮区反射面的每个局部都可以看成是平面,波的反射特性服从局部平面波反射规律[16-17]。

如图2所示,s代表整个散射体外表面,r1和r2分别表示散射体表面元ds到入射点M1和散射点M2的矢径,rs为参考点到ds的矢径;θ1和θ2分别为表面外法线方向n与入射点M1和散射点M2矢径间的夹角,r10、r20为参考点O到M1和M2点的距离,A1、A2为从M1能照射到的亮区的边界点,B1、B2为从M2能照射到的亮区的边界点。

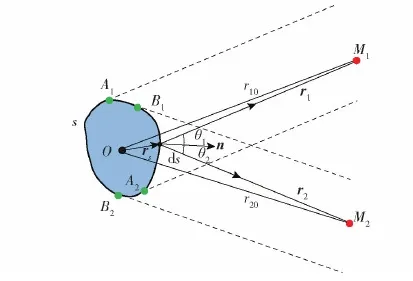
图2 Kirchhoff近似理论推导示意图Fig.2 Schematic diagram of Kirchhoff approximation theory derivation

散射声波势函数满足如下Helmholtz积分公式[18]:

(2)

式中:k为声波数。

考虑散射体为刚性表面下的边界条件,则散射声波势函数为

(3)

式中:A是任意振幅。在收发合置情况下,|r1|=|r2|=|r|,|r10|=|r20|=|r0|,Δr1=Δr2=Δr,θ1=θ2,则式(3)可以表示为

(4)

声波在空气凹槽中来回一次引起的相位差与凹槽深度的关系为

(5)

式中:φi为第i个凹槽处的相位差。

散射声压在凹槽处会发生相位突变,因此等效平面化后需要在凹槽位置处叠加对应的相位[19],第i个凹槽处的散射声波势函数为

φ′s,i=φs,i·ejφ

(6)

式中:φs,i未叠加相位变化时第i个凹槽处的散射声波势函数。

将凹槽之间分割区域和凹槽位置处的散射声波势函数求和,计算其目标强度如下:

(7)

式中:M为凹槽之间分割区域与凹槽的数量。

1.2 基于射线追踪的二面角声学超表面散射声场求解

声波在二面角中的二次散射现象使得散射声场的求解更为复杂,该问题可以简化为两个分立板块间的二次散射问题[20]。

如图3所示,板块1和板块2为一组反射对,O1和O2分别为对应板块中心点,n1和n2分别为外法线矢量,r1为发射点T到板块1中心点O1的矢量,r2为发射点T到板块2上任一点Q的矢量,r12为板块1中心到板块2任一点Q的矢量。在收发合置情况下,从发射点T出发的声波经板块1和板块2的散射后回到接收点T,假设T′为T关于板块1的对称点,称T′为虚源点,r′1为虚源点T′ 到板块1中心点O1的矢量,则以上过程可简化为声波从T′出发经过板块2散射后回到接收点T,进而可以应用板块元方法对散射声场进行计算。

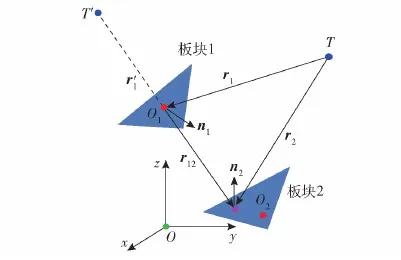
图3 分立板块二次散射示意图Fig.3 Diagram of secondary scattering between discrete plates

根据式(8)可以得到如下二次散射声波势函数:

(8)

在二面角上进行刻槽即可得到二面角声学超表面,二面角声学超表面的散射声场如图4、图5所示。

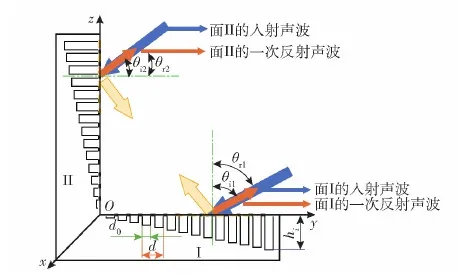
图4 超表面二面角声波一次反射示意图Fig.4 Schematic diagram of the primary reflection of acoustic waves at the dihedral corner of the acoustic metasurface

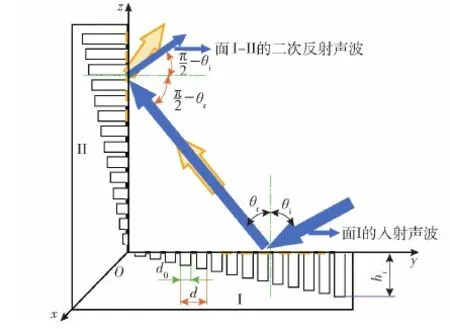
图5 超表面二面角声波二次反射示意图Fig.5 Schematic diagram of the secondary reflection of sound wave at the dihedral corner of acoustic metasurface

图4中θi1和θi2为声波关于面Ⅰ和面Ⅱ的入射角,θr1和θr2为声波关于面Ⅰ和面Ⅱ的反射角,由于本文仅考虑收发合置情况,一次反射的入射角与反射角在法线同一侧。

二次散射声场包含面Ⅰ-面Ⅱ的散射声压和面Ⅱ-面Ⅰ的散射声压,基于几何结构和入射角度的对称性,仅对面Ⅰ-面Ⅱ的散射声场进行说明。二面角声学超表面散射声场计算示意图如图6和图7所示。图6和图7中,Q′为发射点Q所对应的虚源点,θt为声波的透射角,ya和za分别为声波二次散射在二面角上的交点坐标。

图6 二次散射中虚源位置的确定Fig.6 Determination of virtual source position in secondary scattering

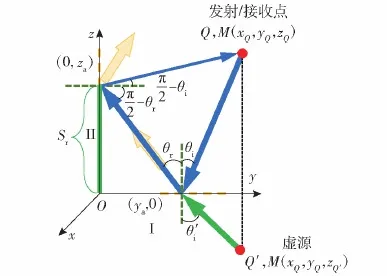
图7 超表面中凹槽的二次散射示意图Fig.7 Diagram of secondary scattering of groove in acoustic metasurface

声波入射到面Ⅰ以及从面Ⅰ二次散射到面Ⅱ上时,根据1.1节中的内容,应对凹槽处声压进行相位修正,进而利用基于虚源法和射线追踪的改进板块元算法,即可求得二面角声学超表面的二次散射声波势函数[21]:

(9)

式中:rQ′i,i为发射点虚源所对应坐标矢量,Q′i为与入射波和超表面交点所对应的虚源点;rM,i为接收点所对应坐标矢量;vQ′,i为发射点对应虚源坐标;vM,i为接收点坐标;Is,Ⅰ-Ⅱ,i表达式为

Is,Ⅰ-Ⅱ,i=∬s,Ⅰ-Ⅱe-jk[xU+zW]dxdz

(10)

U=2xQ,W=zQ+zQ′。

当考虑一次和二次反射时,总散射声场为

φ=φs,Ⅰ+φs,Ⅱ+φs,Ⅰ-Ⅱ+φs,Ⅱ-Ⅰ

(11)

式中:φs,Ⅰ、φs,Ⅱ分别为面Ⅰ、面Ⅱ的一次散射声压;φs,Ⅰ-Ⅱ、φs,Ⅱ-Ⅰ分别为面Ⅰ～面Ⅱ的二次散射声压和面Ⅱ～面Ⅰ的二次散射声压。将总声压代入 式(7), 可得到超表面二面角的目标强度。

2 超表面二面角声散射特性仿真计算

2.1 超表面二面角散射声场计算

为验证超表面对于散射声场调控的有效性以及改进板块元快速计算方法的正确性,实现对散射声场和声散射主方向的调控,针对加载超表面的二面角声散射特征展开研究,讨论不同结构超表面对其散射声场的影响。

基于广义斯奈尔定律[22]可知声学超表面反射角满足α=arcsin[sinθi+2g],其中g为槽阵列梯度。该式与入射波频率无关,因此对声波的操控有较好的宽带效果。

设计具有声学超表面的二面角三维模型,如 图8 所示。该模型槽阵列梯度为固定常数g=dhi/dx=0.1,当入射声波频率f0=c0/2hN=10 kHz(c0=1 500 m/s为水中的声速,hN为最深槽的深度)时,根据式(1)设计的凹槽可产生的相位变化范围为 0～2π rad, 步长是π/5 rad。因此,入射波频率为nf0(n为常数,n>0)时,反射相位变化范围为0～2nπ rad,步长是nπ/5 rad。垂直入射时θi=0°,反射角为11.5°。凹槽宽度为d0=0.072 5 m,结构单元长度为d=0.075 m,凹槽深度从0.007 5 m逐阶递增到 0.075 m, 步长为0.007 5 m,凹槽数量为 10个。 模型总深度H=0.1 m,总宽度D=0.755 m,垂直于纸面的高度l为0.4 m。

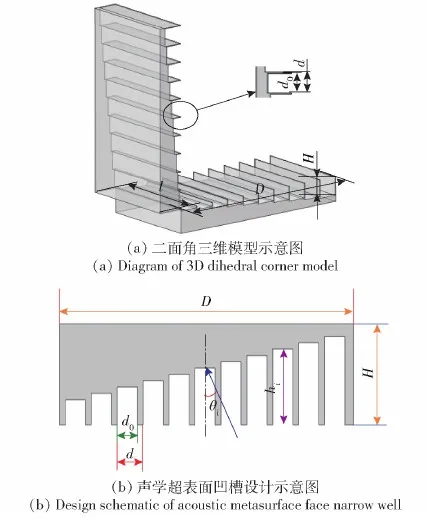
图8 声学超表面二面角设计示意图Fig.8 Schematic of acoustic metasurface dihedral corner design

当入射声波频率分别为10 kHz、15 kHz、25 kHz,入射角度为0°～90°时,分别利用有限元方法和改进板块元方法计算二面角平板以及声学超表面二面角的散射声场,计算结果如图9所示。

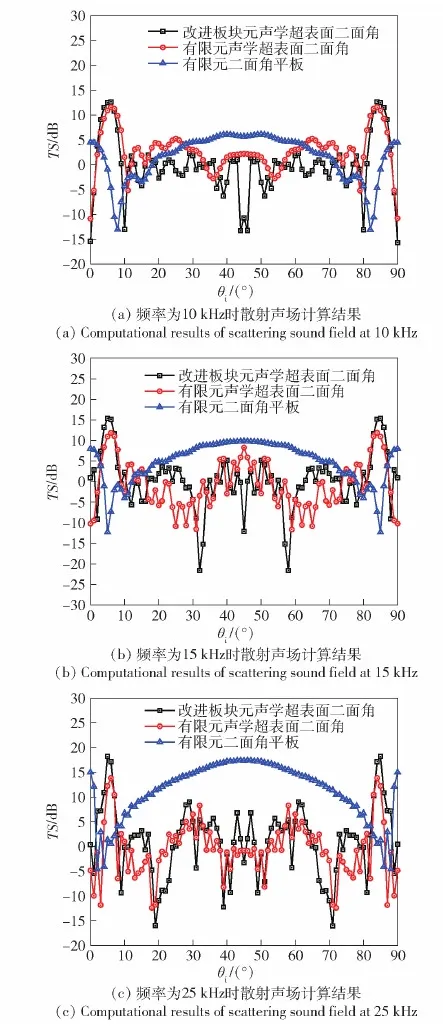
图9 超表面二面角散射声场计算结果Fig.9 Computational results of dihedral angle scattering sound field on acoustic metasurface

在入射声波频率为10 kHz、15 kHz、25 kHz时,通过对比图9中二面角平板和声学超表面二面角的目标强度指向性曲线可知,二面角平板目标强度在入射角为0°、45°、90°时最大,声学超表面二面角目标强度最大值对应的入射角则有所改变。声学超表面二面角的散射声场调控效果较为明显,具体表现为:声学超表面二面角目标强度幅值分别在入射角为28°～62°、16°～74°、7.5°～82.5°时有明显降低;不同入射声波频率下,对于目标强度的调控效果不同,声波频率为25 kHz时,声学超表面二面角模型目标强度削弱效果最明显。这说明了该声学超表面结构在不同入射声波频率下对于降低目标强度均有效果,且对二面角目标强度指向性也有一定的调控作用。

同时,通过对比图9中声学超表面二面角的目标强度有限元法和改进板块元法计算结果,可知在入射角范围为0°～90°时,两种方法计算结果在大部分入射角范围内基本趋于一致,验证了改进板块元方法的正确性。但仍然存在一些误差,分析其原因主要为:1)改进板块元快速计算方法关于凹槽处相位变化只针对平面化的凹槽处进行了叠加相位计算,而有限元方法对于超表面模型中的凹槽并未做近似化处理,凹槽中侧壁也参与到计算结果中;2)当波长小于或接近于凹槽宽度时,声波沿凹槽上下传播时,侧面的多次反射会导致幅值有一定衰减,同时相位也有轻微延迟。因此两种方法的计算结果在一部分入射角度下存在误差。

2.2 声学超表面二面角散射声场影响因素研究

2.2.1 槽阵列梯度

基于广义斯奈尔定律,声波反射角不仅与声波入射频率有关,还与超表面槽阵列梯度有关。

2.2.2 梯度大小

利用广义斯奈尔定律,通过改变槽阵列梯度大小改变声波反射角,实现调控声散射主方向及散射声场。设计槽阵列梯度g分别为0.1、0.2、0.3, 图10 给出不同槽阵列梯度声学超表面二面角模型示意图和入射声波频率为10 kHz,入射角度范围为0°～90°时的目标强度计算结果。

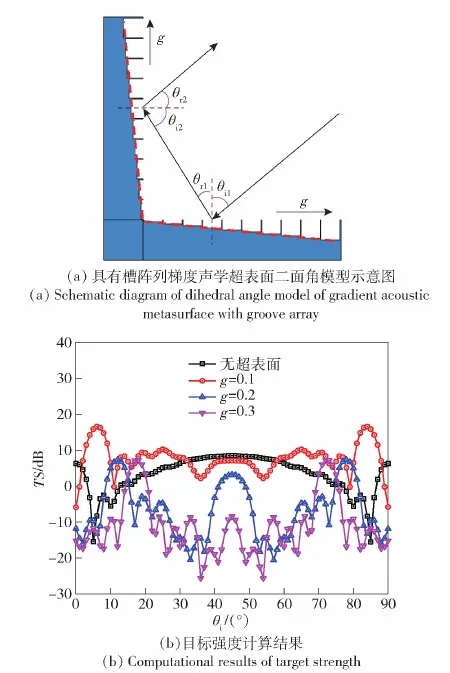
图10 不同槽阵列梯度大小模型及目标强度计算结果Fig.10 Groove array model with different gradients and computational results of target strength

如图10所示,不同槽阵列梯度大小的声学超表面二面角模型对于目标散射声场的调控效果不同。分析图10中目标强度计算结果并对比可得到以下规律:

1)目标强度幅值在大部分入射角度得到了调控,这类结构对于目标强度的调控随入射角度变化升高或降低,并且这类结构关于几何中心对称,所以通过对比无超表面二面角结构的计算结果,产生较大目标强度的入射角度位置明显发生变化,表明这类结构对于声散射主方向调控具有效性。

2)g为0.1时,对比二面角平板目标强度指向性曲线,在入射角为3°～30°、60°～87°范围内超表面二面角目标强度幅值明显升高,并且在入射角为5°和85°附近时,目标强度具有较大值。g为0.2时,在入射角为8°～15°、75°～82°范围内超表面二面角目标强度幅值明显升高,并且在入射角为12°和78°附近时,目标强度具有较大值。g为0.3时,在入射角为14°～20°、70°～76°范围内超表面二面角目标强度幅值明显升高,并且在入射角为17.5°和72.5°附近时,目标强度具有较大值。槽阵列梯度大小不同时,较大目标强度所对应的入射角均不相同,说明不同梯度的超表面结构可使声散射主方向偏移的角度不同。

对比图10中的计算结果可知,声学超表面的目标强度指向性曲线峰值随梯度大小发生明显变化,梯度变大时,两端峰值向入射角45°方向移动,且曲线波动更大产生更多峰值;槽阵列梯度大小对于目标强度幅值的影响同样较为明显,随着梯度的增大超表面结构对目标强度幅值的调控效果从增强变为削弱,其中值得注意的是g为0.1时,目标强度幅值在大部分入射角下明显增强,说明该梯度大小超表面结构可以在较大入射角范围内实现增强水下模拟体目标强度的目的。

2.2.3 梯度方向

不改变槽阵列梯度大小(梯度g皆为0.1),计算正负梯度方向槽阵列的声学超表面散射声场,分析其影响规律。图11为不同梯度方向组合的声学超表面二面角模型示意图以及入射声波频率为10 kHz,入射角度为0°～90°时的目标强度计算结果。

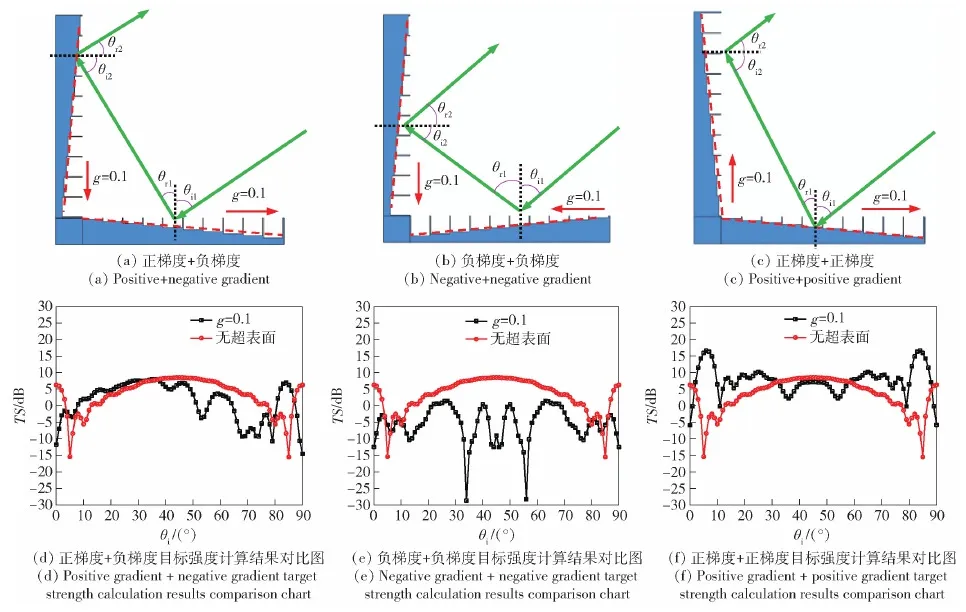
图11 不同槽阵列梯度组合模型及其目标强度计算结果Fig.11 Groove array model with combined gradients and computational results of target strength

如图11所示,加载3种不同槽阵列组合的声学超表面二面角目标强度计算结果有如下规律:

1)图11(d)为图11(a)模型所对应的目标强度计算结果。从图11(d)中可以看出,该槽阵列组合模型的目标强度指向性曲线向0°偏移压缩,表明声波在该声学超表面结构中的传播产生了相位变化,声散射主方向产生偏移,该结构对于声散射主方向调控效果较为明显。

2)图11(e)为图11(b)模型所对应的目标强度计算结果,从中可以看出,相较于二面角平板,加载超表面的二面角目标强度指向性曲线幅值整体降低,在入射角为34°和56°时目标强度幅值差最大,约为35.5 dB,并且目标强度最大时的入射角发生改变。

3)图11(f)为图11(c)模型所对应的目标强度计算结果。当加载超表面结构为正、正梯度时,目标强度指向性曲线发生明显变化,在入射角为32°～58°时目标强度幅值降低,在入射角为2°～32°和58°～88°时目标强度幅值明显升高,在入射角为6°和84°时目标强度最大。

通过上述结果可以看出,本文设计的3种槽阵列组合模型均使二面角的声散射特征发生改变。随梯度正负组合变化,对散射声场产生不同的调控效果,其中正、负梯度槽阵列组合模型对于声散射主方向偏转效果调控更为明显,负、负梯度槽阵列组合模型则对目标强度幅值的调控效果更为明显。对比二面角平板,3种加载超表面的二面角的目标强度指向性曲线波动更大,产生更多波峰,对于目标声散射特征改变明显。因此,通过对二面角平板加载超表面结构改变其声散射特征对于水中目标声伪装具有重要意义。

2.2.4 周期结构

采用2.1节中槽阵列梯度g为0.1的声学超表面为单位周期结构,构建二周期声学超表面结构二面角,对其散射声场特性进行研究。该单位周期结构深度H为0.1 m、宽度D为0.755 m,垂直于纸面的高度l为0.4 m。不同组合结构声学超表面二面角模型示意图及入射波频率为10 kHz时,入射角度为0°～90°时其目标强度计算结果如图12所示。

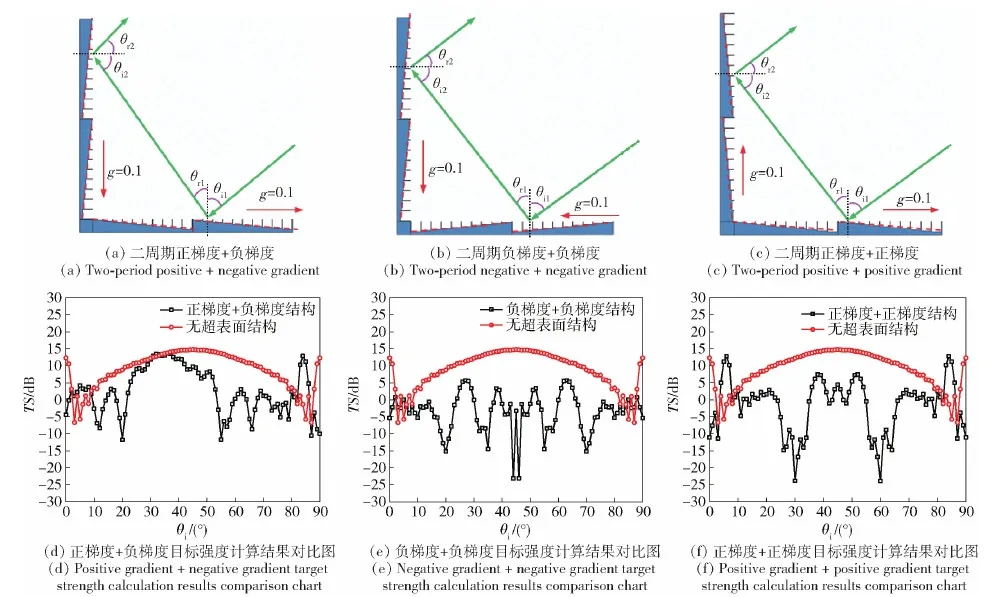
图12 二周期不同槽阵列梯度组合模型及其目标强度计算结果Fig.12 Groove array model of two-period combined gradients and computational results of target strength

如图12所示,加载3种二周期不同槽阵列组合的声学超表面二面角目标强度计算结果有如下规律:

1)图12(d)为图12(a)模型所对应的目标强度计算结果。目标强度指向性曲线向0°偏移压缩,且在入射角为9°～81°时目标强度幅值明显降低,与图11对比加载二周期正、负梯度槽阵列组合超表面对于声散射主方向和目标强度幅值的调控效果更为明显。

2)图12(f)为图12(b)模型所对应的目标强度计算结果。加载超表面结构的二面角目标强度幅值在入射角为0°～90°时明显降低,与图11对比加载二周期负、负梯度槽阵列组合超表面与二面角平板目标强度幅值差距变大。

3)图12(e)为图12(c)模型所对应的目标强度计算结果。与图11对比加载二周期正、正梯度槽阵列组合超表面与二面角平板目标强度幅值之间关系明显发生变化。在入射角为8°～82°时目标强度降低,与单周期该槽阵列组合超表面相比目标强度降低的入射角度范围变大。

与图11对比可知,二周期槽阵列组合声学超表面二面角声散射特征与单周期槽阵列结构有一定差别,目标强度指向性曲线波动更加复杂,产生波峰更多,对比二面角平板声散射特征改变更加明显,并且在大部分入射角范围内,二周期槽阵列组合声学超表面结构对于目标强度幅值降低的效果更强。因此超表面周期数对于降低目标强度幅值和增强声散射主方向偏转程度存在正向影响。

3 结论

本文以广义斯奈尔定律为基础,设计了一种可以在水中对声散射主方向及散射声场进行调控的声学超表面二面角反射体,并提出一种可以对该结构目标强度进行快速计算的改进板块元方法。得出以下主要结论:

1)加载声学超表面对于二面角的散射声场具有调控效果,不同槽阵列组合声学超表面模型对于散射声场的调控效果不同,正、负梯度槽阵列组合对于声散射主方向的调控效果较为明显,负、负梯度槽阵列组合对于目标强度幅值降低效果明显。

2)加载超表面的周期数对于二面角目标强度指向性调控具有影响,增加加载超表面周期可以进一步降低目标强度幅值,并增强声散射主方向偏转程度,同时增强散射声场调控的复杂性和灵活性。

3)在二面角上加载超表面对于其声散射特征具有调控效果,能够明显改变水下目标的声散射特征,由于二面角是水下角反射器的结构基础,研究二面角散射声场调控机理具有十分重要的意义,为水下无源声诱饵的创新设计奠定了基础。