浅析立体几何中的一类动截面问题

■江西省南昌市第三中学 张金生(正高级教师、特级教师)

立体几何试题通常考查点、线、面的位置关系,距离与角的计算,球与多面体的接切,多面体的截面等问题。多面体的截面问题是高考的热点问题,主要考查截面形状的判断,截面的周长或面积,与截面有关的空间角、距离、位置关系等问题。这类问题的一个难点就是如何准确地作出截面,学会截面的作法,对加深空间中点、线、面的位置关系的理解,提高发现问题、提出问题、分析问题、解决问题的能力,提升直观想象、数学建模等核心素养,都有不可忽视的作用。本文通过研究几个有关动截面的试题,力求能帮助同学们攻克这类问题。

例1如图1,已知四面体ABCD为正四面体,AB=1,E,F分别是AD,BC的中点。若用一个与直线EF垂直,且与四面体的每一个面都相交的平面α去截该四面体,由此得到一个多边形截面,则该多边形截面面积的最大值为( )。

解析：如图2,将四面体补形为正方体,点F,E分别为上下底面的中心,直线EF垂直截面MNKL,则截面MNKL与正方体的上下底面平行,由面面平行性质定理知MN∥BC∥KL,NK∥AD∥ML,所以截面MNKL为矩形。如图3,将平面ABC与平面ABD展开在一个平面上,KL+LM=BC=1,截面周长为定值,所以S=KL·LM≤。故选A。

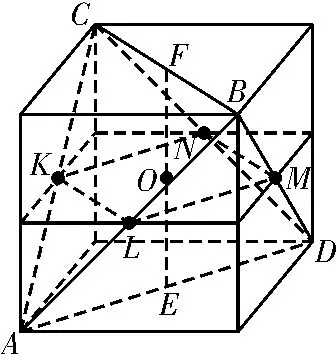
图2

图3

评注:当题目中有切割或折叠时,同学们就应该想到补形或展开,这是解决这类问题的通法。高考试题中那些组合体及非规则几何体问题,需要用割补思想来灵活求解。

例2在正方体ABCD-A'B'C'D'中,任作平面α与对角线AC'垂直,使得α与正方体的每个面都有公共点,记这样得到的截面多边形的面积为S,周长为l,则( )。

A.S为定值,l不为定值

B.S不为定值,l为定值

C.S与l均为定值

D.S与l均不为定值

解析：如图4,将正方体切去两个正三棱锥A-A'BD与C'-D'B'C后,得到一个以平行平面A'BD与D'B'C为上、下底面的几何体V,V的每个侧面都是等腰直角三角形,截面多边形W的每一条边分别与V的底面上的一条边平行,将V的侧面沿棱A'B'剪开,展开在一个平面上,得到一个如图5 所示的平行四边形A'B'B1A1。而多边形W的周界展开后便成为一条与A'A1平行的线段,如图5中的E'E1,显然E'E1=A'A1,故l为定值。当E'为A'B'的中点时,多边形W为正六边形;当E'移至A'处时,W为正三角形。易知周长为定值l的正六边形与正三角形的面积分别为,所以S不为定值。故选B。

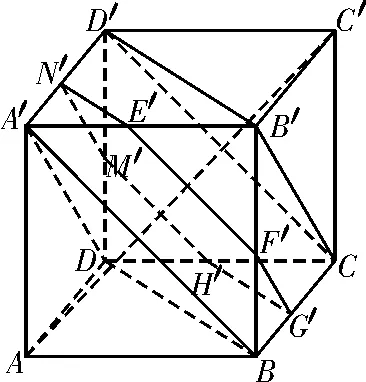
图4

图5

评注:该题与例1 一样,截面周长为定值,面积在变化有最大值,对直观想象要求高,同学们可以动手做个模型更便于理解。

例3已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则平面α截此正方体所得截面面积的最大值为( )。

解析：如图6 所示,在正方体ABCD-A1B1C1D1中,已知平面AB1D1与棱A1A,A1B1,A1D1所成的角都相等,又正方体的其余棱都分别与A1A,A1B1,A1D1平行,故正方体的每条棱所在直线与平面AB1D1所成的角相等。取棱AB,BB1,B1C1,C1D1,DD1,AD的中点分别为E,F,G,H,M,N,则正六边形EFGHMN所在平面与平面AB1D1平行且面积最大,此截面面积为S正六边形EFGHMN=6×。故选A。

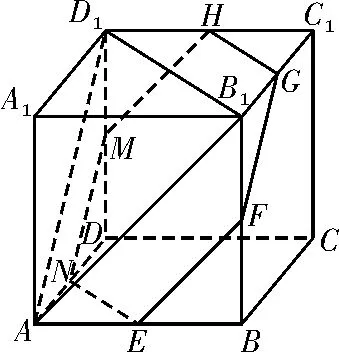
图6

截面问题本是个难点,加上运动变化后更是许多同学的痛点,“动”与“静”是事物的两个方面,深入挖掘几何体结构的本质特征,从直观感知、操作确认、推理论证、度量计算等视角探索研究空间图形的性质,在动的表象下探寻运动过程中“静”的一面,动中求静,以静制动,克难制胜。