数形结合明算理 构建模型悟规律
朱兰
在小学数学学习中,说到学生的高频错题一定有乘法分配律的运用。乘法分配律无论从形式还是内涵来看,比起乘法交换律和结合律等其他运算律都更加复杂。乘法分配律往往因其形式复杂、运用广泛、变式较多,成为老师的教学难点和学生的易错内容。在对老师的访谈中了解到,大多数老师教学这个内容都是从不同综合算式中因结果相同建立等式,学生写出等式,并用字母表达总结出乘法分配律。这样的数学模型建构方式学生只记住了“形”,而无法明白“理”。这也是学生面对形式多样的乘法分配律时漏洞百出的原因。《义务教育数学课程标准(2022年版)》(以下简称课标(2022年版))指出:“通过实际问题和具体计算,引导学生用归纳的方法探索运算律、用字母表达运算律,感知运算律是确定算理和算法的重要依据,形成初步的代数思维。”通过对教材、学生学情前测以及教师访谈的分析,笔者认为要构建乘法分配律数学模型要通过具体的乘法情境,用“数形结合”的方式从乘法的意义来理解乘法分配律的内涵,形成规律的一般性表达,积累学习经验,为后续的学习和代数思维的发展提供基础。
一、巧用主题图设计有价值的数学问题,数形结合引入等式
师:劳动使人快乐,种菜已成为当下重要的劳动实践活动。今天我们一起来研究菜园里的数学知识。
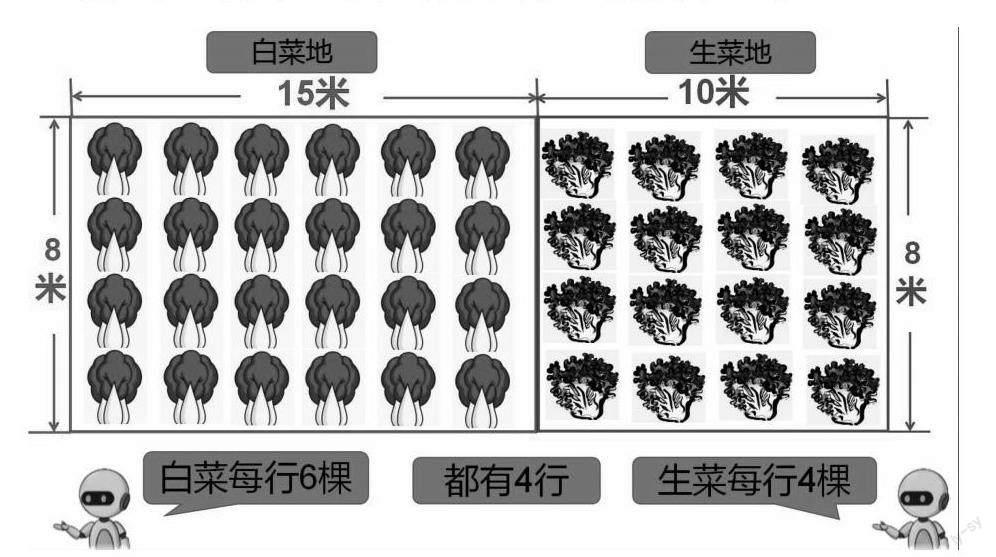
师:你能根据这幅图提出并解答两个两步计算的问题吗?你们提出哪些数学问题?
生:一共有多少棵菜?
师:请说说你列的综合算式并结合图说清楚综合算式每一步表示的意义。
生1:用(6+4)×4,白菜每行6棵,生菜每行4棵,先用6+4算出它们合起来一行有10棵,乘以4,就算出了一共有多少棵菜。
生2:我的方法和他的不同,是6×4+4×4,我用白菜每行有6棵,有4行,6×4算出白菜有几棵,再用生菜每行有4棵,有4行,4×4算出生菜有几棵,最后白菜棵数加生菜棵数就算出菜地的总棵数。
师:这两个算式都解决了同一个问题,观察这两种解法,有什么不同的地方和相同的地方?
生:它们方法不同,一个是合起来算,另一个是先分开算再合起来,它们都有共同的4行。
师:这个4在乘法里叫什么?(学生答因数)也就是都有相同因数。还有什么相同?
生:两个算式得数相同。
师:得数相同我们数学上可以用哪个符号连起来(生答等号)。这样就形成了一个等式(6+4)×4=6×4+4×4。
评析:用同样的方法学生结合图交流了菜地一共有多少平方米?同样发现方法不同,但有相同因数且得数相等,形成了第二个等式(15+10)×8=15×8+10×8。《新课标》要求:“能解决生活中的简单问题,并能对结果的实际意义做出解释,经历探索简单规律的过程。”学生在解决两个现实问题中利用数形结合理解了算式的实际意义得到了两组等式,观察中感悟分配律两式相等的关系。
二、不断积累经验,深度理解等式的意义
出示题目:给菜园栅栏刷油漆,蓝色油漆需要3桶,红色油漆需要2桶,每桶都是90元。
师:带着你对前面等式的感觉,你想提出一个什么数学问题?
生:一共要花多少元?
师:你能用两种方法解答这题吗?可以写成上面的等式吗?
生:(3+2)×90=3×90+2×90。
师:怎么证明它们是相等的?
生:得数相等,等式左右得数都算得450元。
师:除了得数相等,还可以怎么证明它们是相等的?
生:等式的左边和右边都表示5个90。
师:等式的左边和右边都表示5个90,也就是它们的意义相同。这个同学用乘法的意义说明了等式相等。合起来等式两边都表示5个90,再分开来看算式意义,谁来说一说?
生:(3+2)个90=3个90+2个90。
师:你们能模仿上面编写一组同样规律的等式吗?请用乘法的意义来说明等式写对了。
师:你们寫了,我也想写一组,(2+4)×8=2×8+8。写对了吗?怎么改?我们从算式的意义来检查就很容易找到问题。
评析:针对传统的只注重“形”的教学,为了让学生更好地明“理”,从意义出发构建乘法分配律显得尤为重要。在实际问题情境中从乘法的意义几个几相加来深入理解乘法分配律的本质,突破了乘法分配律的难点。这个环节的构建是本节课的核心,意义的理解帮助学生对乘法分配律更好地建模,同时从后期的测评中看出对意义的理解,大大提高了练习的正确率和简算的变式运用。
三、观察等式分析归纳规律,逐步抽象构建模型
师:我们横向了解这些等式得数相同,有相同因数,意义相同,那我们纵向地看看这些算式的特点?
生1:左边的等式是合起来算,右边的是分开算。
生2:左边是先求和再相乘,有括号、加号、乘号;右边是先分开乘再合,有两个乘号和一个加号。
师:这样的等式你们能写出多少?
生:无数个。
师:既然写也写不完,那你们能用最简单的数学语言归纳出所有这一类等式的规律吗?
生1:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。
生2:(甲+乙)×丙=甲×丙+乙×丙。
生3:(a+b)×c=a×c+b×c。
师:用字母能代表上面所有的算式吗?用字母表达你感觉怎么样?(数学符号的简洁美)
师:大家发现的这一类规律你知道叫什么规律吗?(板书课题)为什么要叫乘法分配律?你怎么理解分配?来结合字母表达式说一说。
评析:学生在观察算式特点中发现,括号先算之后,就没有括号了,也就是从合起来算到分开来算,充分理解了乘法分配律的形式。从算式中理解了乘法分配律的本质内涵,这只是具象的理解,更需要对概念的抽象和升华。《课标(2022年版)》提到学生“能用字母表示运算律”“能说出运算律的含义,并能用字母表示”。教师用“你们能用最简单的数学语言归纳出所有这一类等式的规律吗?”启发学生用数学语言概括这一类等式的规律形成一般性的表达。学生逐步经历了从语言表达到符号表达的转化过程,在不断抽象的过程中建立数学模型,体会数学的简洁美。给发现的规律取名字和理解“分配”这个词,实际是让学生说出自己对规律的理解,是学生对规律理解的外显方式,丰富了学生对规律的认识和理解。
四、循序渐进的练习,沟通知识间的联系,提升规律运用
1.填一填。直接用算式的意义边说边填。
(42+35)×2=42×_______ +35×_______
27×12+43×12=(27+_______)×_______
15×26+15×14=_______×(_______+_______)
(a+b)×9=a×_______+_______×_______
2.回顾沟通,建立联系。
其实乘法分配律大家不是第一次见,在学习两位数乘一位数的口算时,16×3就是先把16分成10和6,再与3相乘。在两位数乘两位数中23×12,把12分成10和2,再分别与23相乘,最后相加。学习长方形的周长计算时,可以用长×2+宽×2,也可以用(长+宽)×2,这些都是乘法分配律的运用。后面你们学到的简便计算和一些解决问题都能找到乘法分配律的影子。
3.融会贯通,知识拓展。
在同学们课前做的导学单中有同学提出了这样的问题:白菜比生菜多几棵?也用了两种不同的解法,这里有乘法分配律吗?我们下节课来研究。今天学了乘法分配律,你还想研究什么?
评析:练习设计了三个层次:从基本概念练习到沟通以往学习中乘法分配律的运用,最后到后续学习乘法分配律变式的铺垫。层层递进,目的是让学生运用形成的乘法分配律模型去解决问题,去与旧知识建立联系,去思考后续相关知识学习。从而获得知识的再现、重组和升华,加深了对数学模型的理解,凸显了模型思想的建构价值。
本案例设计重在通过数形结合和对等式意义的理解,从具象到抽象地让学生真正理解乘法分配律的内涵。设计中从实际问题出发,让学生经历了在具体情境中理解乘法分配律的概念、解释等式两步的等值关系、用字母表示规律等方式逐步构建数学模型,发展学生初步的代数思维。

