基于激光雷达数字高程模型的重力勘探地形改正方法

邱隆君，孙诚业*，杨亚斌，吴新刚

（1. 中国地质科学院地球物理地球化学勘查研究所，河北廊坊 065000；2. 国家现代地质勘查工程技术研究中心，河北廊坊 065000）

0 引言

重力勘探是一种传统的地球物理勘探方法，是对实测重力数据进行自由空气校正、中间层校正、地形校正、正常场校正等预处理获得布格重力异常［1-2］，再用场分离技术和重力反演方法获得地下密度异常体的位置信息或者密度信息［3-4］的一种间接勘探方法。

在数据预处理阶段，为了消除起伏地形密度体的干扰，需要进行地形改正。它的计算过程主要考虑两个方面：第一，对起伏地形选择恰当的密度数值。既可选择能代表研究区地层特征的密度值，也可以按照有关规范设定岩石密度、海水密度、淡水密度［5-6］。第二，结合实际的地形改正范围选择合适的地形数据库。一般近区和中区地形改正范围为0～2000 m，采用空间分辨率和精度较高的地形数据库，如应用高精度差分卫星定位测地技术（GPS-RTK）或航摄获得的高精度数字高程模型（DEM）数据［7］；远区地形改正范围为2000～166700 m，需要覆盖率较高的地形数据库，如航天飞机雷达地形测绘使命（SRTM）或高级星载热发射和反射辐射仪（ASTER）得到的DEM 数据。

地形数据库的空间分辨率、精度、覆盖率都会影响计算结果，分析某单一变量难以清晰地论述这些关系。因此，地形数据库是全面、深入地研究地形改正的各种影响因素及其影响程度的关键要素。全站仪或GPS-RTK 方式获取的高程数据精度最高，但成本高，工作效率低；航天遥感技术与空间测量分析技术的快速发展将地面测量获得DEM 转变为由主动遥感方法自动生成DEM［8］，其中激光雷达（LiDAR）在获取大范围、高精度、多种DEM 方面的效率较高，明显提升了大比例尺地形测绘和勘察效率［9］。

一般假设地形体的密度为常数，基于DEM 地形改正的主要研究内容包括地形数据水平分辨率与计算精度之间的关系［10-12］、不同数据源的地形改正精度要求［7］。由于单一源的高分辨率数据的覆盖范围有限，地形改正方法的精度评价都是基于某一个数学模型的假设条件，只能讨论高程测量误差对地形改正的影响，不能分析由扇形锥、扇形柱等数学模型近似实际地形产生的误差。目前，利用LiDAR 数据分析陆地重力近区地形改正数学模型产生的近似误差以及中区地形改正的影响因素的文献较少。

本文采用美国地调局三维高程计划（3DEP）的LiDAR 高程数据，选择12个数据区作为研究对象，利用LiDAR 高程数据为参考数据，以直棱柱模型重力解析式计算结果为地形改正参考值，从统计角度对比近区和中区地形改正的数学模型和计算方法的精度，这是本文的主要创新点；在此基础上，分析不同计算方法、不同地形网格间距的差异，并且对比不同方法的计算效率。

1 数据说明

美国地质调查局从2016年至2023年实施3DEP，目前可公开访问的高程数据的最高精度为1 m×1 m，即栅格尺寸为1 m×1 m，数据维度为10012×10012，高程值为由机载LiDAR 扫描获得的初始数据经滤波得到的裸露地表高程［13］。本文选用3DEP 高程数据集中地形起伏特征明显的12 个DEM 为试验数据区，其地理位置分布见图1。在生产过程中会融合其他数据，因此最终数据产品的精度并不统一。基于地貌划分原则，试验区的地貌包括丘陵（海拔<500 m，相对高度<200 m）、中山（海拔为800～3500 m，相对高度>500 m）、高山（海拔>3500 m，相对高度>500 m），详细的统计数据见表1，数据下载网址为：https：∥www.usgs.gov/3d-elevation-program。

表1 机载激光雷达DEM 统计表

3DEP提供的原始数据的水平分辨率为1 m×1 m，为平面投影后数据，与ASTER GDEM（全球DEM）等以经纬度表示的数据不同，更适合作为重力近区和中区地形改正的试验参考数据。为分析不同网格间距对地形改正精度的影响，将1 m×1 m 栅格数据进行“粗网格”处理，处理过程的本质是“平滑”原始数据，使地形更“平缓”。以栅格数据存储DEM 的数据空间排列都是有规律的，有些情况需要平面坐标变换，如ASTER GDEM 高程数据，具体方法见下文。每个栅格像元的数值表示该像元覆盖面积内的平均高程，这与节点高程数据只表示单一位置高程信息的本质不同。

2 近区与中区地形改正方法

2.1 近区地形改正方法

根据区域重力调查规范，1∶5 万比例尺近区地形改正半径为20 m，其他比例尺的近区地形改正半径为50 m［14-15］。采用八方位圆域法计算时，内环一般采用扇形锥模型（图2a），外环采用扇形柱模型（图2b）。扇形锥模型的地形改正为［16］

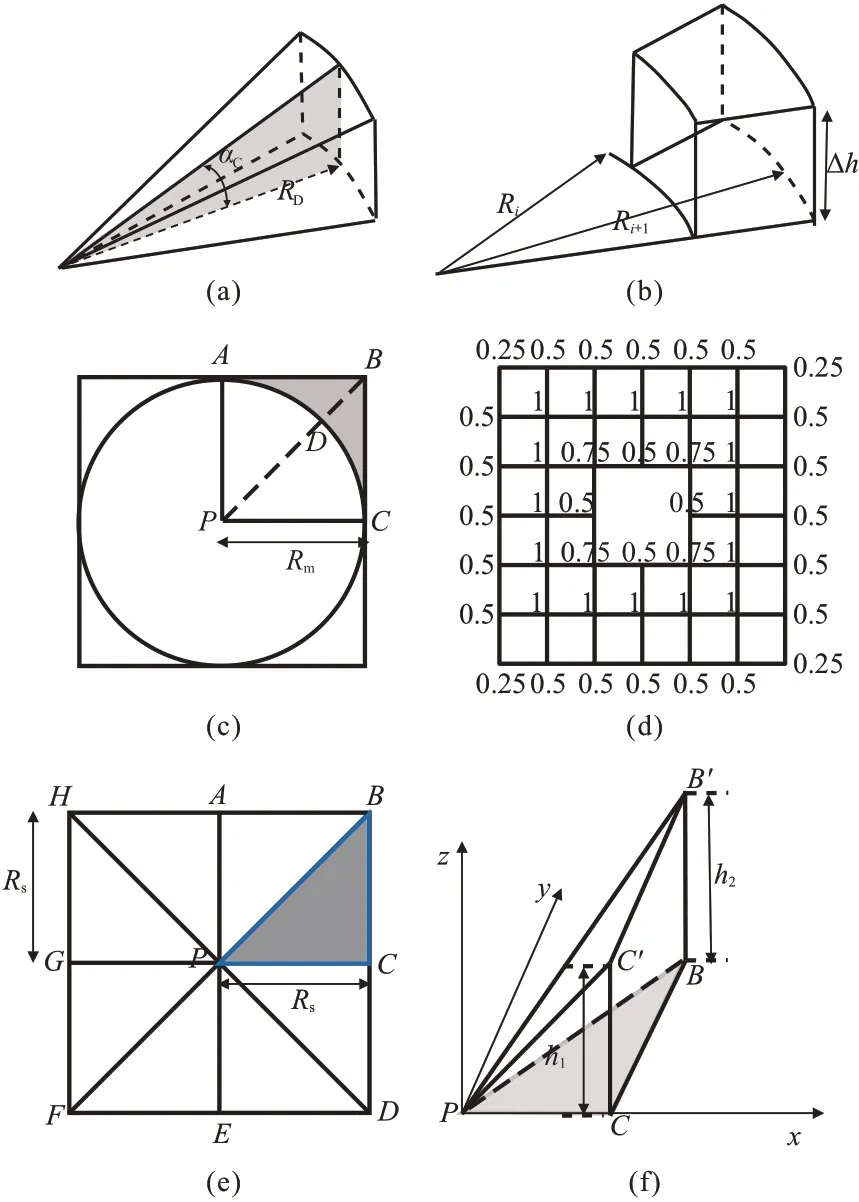
图2 近区和中区地形改正采用的数学模型

式中：G、RD、nc、αc分别为万有引力常数、近区地形改正半径、方位数、扇形锥顶面中心线与其平面投影线间的夹角；σ为模型密度。

扇形柱模型的地形改正为

式中：Ri为第i环的半径；Δh为扇形柱相对于测点的平均高差；np为方位数。

对于方域近区地形改正，重力规范中一般采用由测点P、角点B以及边长中点C构成的斜顶面三角棱柱模型（图2e和图2f）计算地形改正值，模型整体与扇形锥模型类似，不同的是该模型高度主要受角点和边长中点的控制。基于该模型的方域近区地形改正为

其中

式中：h1，j、h2，j（j=1，2，…，8）分别为第j个斜顶面三角棱柱单元的中点和角点相对于测点的高差；Rs为方域近区地形改正半径。

2.2 圆域数据与方域数据接口处理

分环、分方位进行重力近区地形改正要将实际地形数据按照圆域数据处理，而高精度重力中区地形改正通常采用规则网格的高程数据。这些数据通常以附带平面投影坐标或者附带大地坐标信息的栅格数据存储，在平面上坐标数据通常以方域显示。在调用这些方域数据对某个测点进行中区地形改正时，还需要计算近区圆域数据与中区方域数据的间隙产生的地形改正值（图2c的灰色充填部分），这一部分质量产生的地形改正值要累加到近区圆域地形改正值中——数据接口处理，在重力调查规范中也称为内接口补角计算。

区域重力调查规范给出的内接口补角地形改正的简化公式为

式中Rm、Δhc分别为近区地形改正半径、补角重心高程与测点高程差，而

其中

为权重系数。式中：xm、ym和Hm分别为补角范围内代表高程特征的点的平面坐标和高程；xP、yP和HP分别为测点的平面坐标和高程值，通常计算Δhc需要四个高程数值和对应的权重系数，如图2c 的A、B、C及D四点的高程数据及其权重系数。由式（7）可知，wA=

夏江海［17］给出补角地形改正的修正公式

2.3 中区地形改正方法

中区地形改正方法的实现取决于采用的数学模型。通常采用直棱柱模型解析式求解，或采用二重梯形积分快速计算，还可以采用倾斜顶面棱柱模型，利用表面积分法近似计算。理想模型数值模拟表明，高斯表面积分法的计算精度高于二重梯形积分公式。可将棱柱体质量压缩至中心垂线上——质量线模型，这种简化模型的计算表达式简洁、计算速度较快。以下讨论直棱柱模型解析式的离散形式、质量线模型方法、直棱柱模型的二重梯形积分方法及基于三角面元的表面积分方法。

2.3.1 直棱柱模型解析式

根据区域重力调查规范［14-15］，中区地形改正采用平顶面棱柱模型计算公式，某点的水平坐标和高程为(xk，yq，hkq)，即表示x方向第k个、y方向第q个直棱柱顶面中心坐标及其高程；测点的水平坐标和高程值为(xP，yP，hP)。假设该测点进行中区地形改正的范围共包含J×I个矩形棱柱，那么全部直棱柱产生的总地形改正为

式中：(x，y，z)为相对坐标，坐标原点位于直棱柱顶面中心；r为直棱柱顶面中心到测点的相对距离；∆h=hkq-hP，表示直棱柱顶面中心与测点的高程差；∆x、∆y为直棱柱的水平尺寸。

应用上述公式计算测点的中区地形改正时，需要排除近区范围的直棱柱模型的影响，避免重复计算。

2.3.2 质量线模型方法

基于质量线模型的计算是将三重积分进一步简化为离散的二重积分形式，即

式中：rkq为 质量线到测点的水平距离；(∆x)kq、(∆y)kq为某一个直棱柱的水平尺寸，由于(∆x)kq、(∆y)kq在累加求和符号内部，因此能够对不同尺寸模型单元进行计算。

2.3.3 直棱柱模型的二重梯形积分方法

利用高斯公式将地形质量引力场的三重积分转化为二重表面积分，在测点数千米范围内进行地形改正可忽略地球表面弯曲影响。由于地形体的外边界的侧面与高程基准面互相垂直，其法线与z轴垂直，因此在侧表面的积分结果为零，其余为地形高程基准面（大地水准面）以及起伏地形表面的积分结果，即

式中：rkq为直棱柱顶面中心到测点的水平距离；Sd表示高程基准面；St表示地形起伏表面。当用直棱柱单元划分地形时，式（11）近似为梯形积分表达式

式中Ckq为选用的梯形积分系数，其中内节点系数为1，边缘点系数为0.5，外角点系数为0.25，内角点系数为0.75，系数具体分布见图2d。当近区和中区间的边界通过原始栅格时，需要测点附近的四个高程节点（高程数值仍为测点的高程值）的地形改正值，再进行双线性插值，从而获得测点的地形改正近似计算结果，此方法称为共用点法。

2.3.4 基于三角面元的表面积分方法

基于散度定理，将式（11）的体积分转换为起伏地形和地形高程基准面包围区域的表面积分，这两部分通过三角面元离散，再利用高斯积分等数值积分方法估算每个三角面元的积分近似结果，最后累加求和。地形改正近似表示为［18］

其中

式中：(xα，yα，zα)、(xβ，yβ，zβ)以及(xη，yη，zη) 分别为第n个三角面元的三个顶点的空间坐标；为第u个节点的空间坐标；1，2，3；u=1，2，…，NQ)为节点坐标，NQ 为使用的高斯节点数目；Wu为求积权重系数；L为规则数字化网格的网格间距，L2/2为三角面元在水平面上的投影面积；NE 为离散的三角面元总数。本文采用三点高斯积分公式［19］，节点的面积坐标分别为(0，0.5，0.5)、(0.5，0，0.5)、(0.5，0.5，0)，求积权重系数分别为1/3、 1/3、 1/3。

2.4 大地坐标高程数据的处理

目前，公开访问的ASTER GDEM、SRTM 等高程数据都采用WGS-84大地基准，由理论地球位场模型EGM96 推导的大地水准面为高程基准，计算栅格像元的沿经线方向尺寸为∆Mx，与沿纬线方向尺寸为∆My，即

式中：φe、∆φe以及∆L分别为栅格像元的地心纬度、地心纬度跨度以及经度跨度；re为栅格像元到地心的距离。实际计算中，全部栅格像元水平尺寸的转换过程是一项繁琐的计算过程，由于中区范围一般在测点周围2 km 以内，因此可以利用测点位置地形模型单元的水平尺寸代替测点周围全部栅格像元的水平尺寸，可极大地减小计算量。某一测点位置附近的栅格像元尺寸为

式中：∆B为栅格像元纬度跨度；NEGM96为利用WGS-84 椭球参数和EGM96 地球重力位模型计算的大地水准面高度；φe可由测点的大地纬度B换算；rE为WGS-84 椭球面的半径，它是φe与第二偏心率e′的函数，即

式中e′2=(a2-b2)/b2，其中参数a、b分别为参考椭球的长半轴和短半轴。φe与B满足

综上所述，近区地形改正方法既可采用扇形锥与扇形柱的混合模型，也可仅采用扇形锥模型，而斜顶面三角棱柱模型可避免圆域与方域数据接口问题。中区地形改正方法中直棱柱模型解析式的精度最高；梯形积分与三角面元积分都是三维体积分的二维化简形式，其中三角面元积分通过调整积分阶数提高计算精度，是较灵活的计算方法；质量线模型方法是将模型化简的方法。

3 数值试验

3.1 误差分析与数值试验环境

重力勘探近区和中区地形改正的计算精度及其改善方法一直以来都是关注重点。图3 为重力中区地形改正的工作流程。从实际地形通过某种测量手段（水准测量、机载激光雷达等）获得数字高程数据，或者直接从测绘局申请数字高程数据，该过程存在测量误差（包括点位误差和高程误差）和DEM 处理误差。在获得研究区完整DEM 后，利用某种数学模型进行重力近区和中区地形改正，该过程会引入模型近似误差及其计算误差，这两种误差通常难以分离。本文默认模型近似误差包括计算误差，作为主要研究对象。

图3 重力中区地形改正的工作流程

区域重力规范［14-15］一般都假定密度为常数，基于某种数学模型及其公式讨论高程精度以及点位误差对重力地形改正精度的影响，如杨亚斌等［20］利用扇形、锥形和扇形柱公式计算理论误差。

本文以机载LiDAR 高程数据为参考，衡量不同数学模型产生的模型近似误差以及网格间距对地形改正精度的影响。假定地形密度为常数，忽略实际地层密度不均匀产生的影响，全部数值试验均在Intel Core i7-11800H CPU（8 核、基准频率为 2.30 GHz）、64 GB RAM 的移动工作站、Windows 10 操作系统的计算环境下完成，采用基于MEX 文件的Matlab 2020b 并行计算方法。

3.2 近区地形改正的模型近似误差

以往评价近区地形改正精度时以扇形锥、扇形柱以及三角棱柱等理论模型获得的地形改正值为参考值［20］，忽略数学模型近似产生的差异。本文以1 m×1 m 间距的高程数据为参考数据、直棱柱模型重力解析式计算结果为参考值，评价常用数学模型的近区地形改正精度。采用八方位圆域或者方域三角棱柱计算方法，近区地形改正的范围分为0～20 m与0～50 m两种，形成7种计算方案（表2）。可见，既可以单独使用扇形锥或者三角棱柱单一模型进行近区地形改正（Ⅰ、Ⅱ、Ⅲ与Ⅳ），也可以内环采用扇形锥、中环和外环采用扇形柱的混合模型方案（Ⅴ、Ⅵ与Ⅶ）。为模拟野外情况做如下约定：基于1 m×1 m网格数据，以间隔45°读取1 个高程数据。如方案Ⅶ中采用3环，环的外边缘到测点距离分别为10、25 和50 m，利用计算机程序读取原始地形每个方位的半径为10、17.5、37.5 m 圆上的高程节点值［21］，内环利用扇形锥、中环和外环利用扇形柱模型计算后累加求和。

表2 近区地形改正的七种计算方案

近区地形改正值试验设定如下：每个试验区中央6000 m×6000 m 范围内，平均分布间距为100 m的3721(61×61)个测点，测点高程为1 m×1 m 网格的高程值，12 个试验区一共有44652 个测点。由于近区范围为圆域，在近区分界线的直棱柱模型只有一部分处于近区范围，为保证计算严谨性，将这些模型单元细分为更小的棱柱，利用质量线模型方法计算小棱柱体在测点的地形改正值。

计算每种计算方案的计算值与参考值的差异，利用该差异的最大值（10-8m/s2）和平均相对误差进行评价。差异最大值反映了每一个试验区3721 个测点在近区地形改正时由模型近似产生的最大误差；平均相对误差定义为试验区内各测点差异值的绝对值的总和与各测点参考值的总和的比值（用百分比表示），是整体评价不同方案计算精度的指标。

图4 为近区地形改正不同计算方案的差异最大值对数曲线。由图可见：①不同计算方案得到的差异最大值与近区地形改正半径有直接关系，差异最大值通常集中在Ⅱ和Ⅳ，即使八方位Ⅶ的最大差异值在某些试验区仍高于Ⅰ、Ⅲ和Ⅴ。②单一模型方案（Ⅰ、Ⅱ、Ⅲ和Ⅳ）的最大差异值较大，混合模型方案有效降低了最大差异值。③差异最大值与地貌密切相关，如Ⅱ、Ⅳ和Ⅵ中，大于550×10-8m/s2的差异最大值出现在高山（C 区和G 区）。值得注意的是，虽然K 区（丘陵）的高程数据标准差只有36.2 m，但是其差异最大值与J 区（中山）相当。由于人工开采，L 区形成环状阶梯式台阶，高程范围为［1472 m，3081 m］，标准差为358.4 m，是相对复杂的地貌区，然而不同计算方案的差异最大值却处于一个量级（最小为135×10-8m/s2，最大为187×10-8m/s2)，即不同方案的差异最大值变化不大。以上分析说明，不能单独以高程数据的范围和标准差判定地貌对近区地形改正的影响，如地形起伏较平缓的丘陵的差异最大值与中山相当，而地形复杂的露天铜矿区的差异最大值大致处于同一量级。

图4 近区地形改正不同计算方案的差异最大值对数曲线

图5 为近区地形改正不同计算方案的平均相对误差曲线。由图可见：①Ⅰ、Ⅲ、Ⅴ的平均相对误差曲线的变化趋势一致，计算精度从高到低的排序为Ⅴ、Ⅲ、Ⅰ，特别是Ⅴ可以保证K 区以外的11 个试验区的平均相对误差小于20%。②Ⅱ、Ⅳ、Ⅵ、Ⅶ的平均相对误差曲线的变化趋势相近，计算精度从高到低的排序为Ⅶ、Ⅵ、Ⅳ、Ⅱ，其中八方位Ⅶ使全区的平均相对误差小于13%，计算精度最高。③在相同计算方案情况下，K 区的平均相对误差高于其他区；L 区的平均相对误差总体上小于15%。

图5 近区地形改正不同计算方案的平均相对误差曲线

除了差异最大值和平均相对误差外，也可以使用绝对误差值小于50×10-8m/s2的测点数与总测点数的比值（频率）评价近区地形改正的精度。图6为A 区Ⅳ、Ⅵ和Ⅶ的绝对误差直方图及绝对误差—地形标准差散点图。由图可见：①相对于Ⅳ，Ⅵ和Ⅶ的绝对误差更趋向于零误差区间分布；Ⅳ、Ⅵ和Ⅶ的频率分别为0.554、0.772 和0.926，因此八方位Ⅶ是非常有效的计算方案，将使约90%测点的模型绝对误差小于50×10-8m/s2。②地形标准差小于20 m 的测点数占总测点数的98.1%，地形标准差小于10 m 的测点数占总测点数的45.2%；由于Ⅵ和Ⅶ引入扇形柱体模型，因此误差散点逐渐向零误差线收敛、聚集。文中将Ⅳ、Ⅵ和Ⅶ用于12 个试验区并统计了频率（图7）。可见，除了C 区与G 区，在其他试验区Ⅶ的频率都大于0.97；与Ⅳ相比，Ⅶ明显提升了12 个试验区的频率，即频率提升最小值为0.059、最大值为0.539、平均值为0.274。

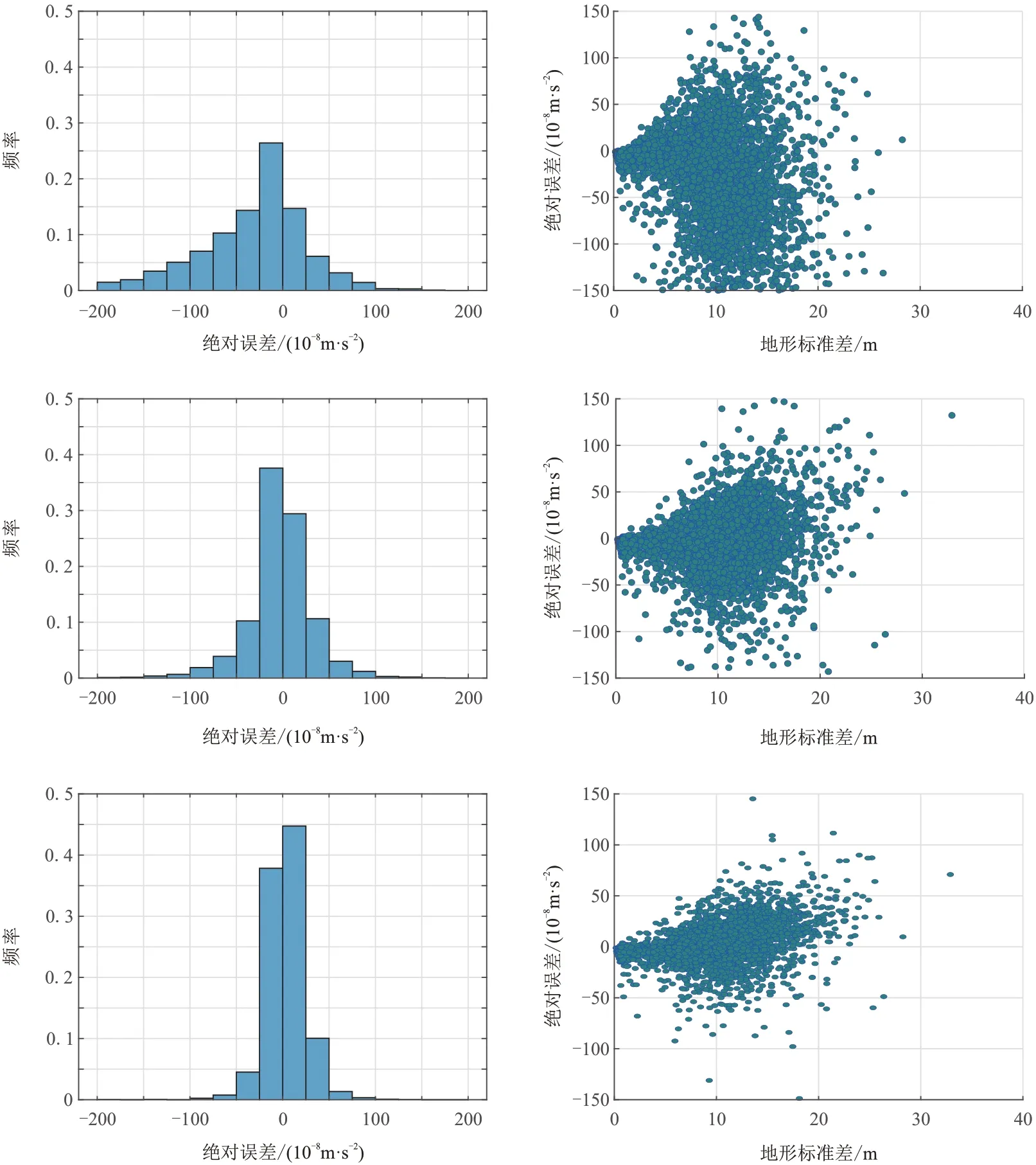
图6 A 区 Ⅳ（上）、Ⅵ（中）和Ⅶ（下）的绝对误差直方图（左）及绝对误差—地形标准差散点图（右）

图7 近区地形改正不同计算方案的频率

3.3 内接口补角计算方法对比

根据式（5）与式（8），对12 个试验区的全部测点的东北补角进行计算，采用质量线公式计算补角地形改正的参考值。对比每个试验区3721 个测点的计算结果与参考值，并统计每个试验区全部测点的差异最大值（10-8m/s2）以及平均相对误差（图8）。可见：式（8）降低了补角地形改正的差异最大值，幅值降低了约(2 ～ 8)×10-8m/s2(图8a)；若不计入J 区与K 区的计算结果，由式（8）得到的平均相对误差都小于20%（图8b）。表1 表明，J 区与K 区为地形最平缓的地区，因此补角地形改正值很小，一般都在10-11m/s2量级。值得注意的是，K 区作为典型的丘陵区，地形相对起伏只有36.2 m，但由式（8）得到的平均相对误差大于90%，因此推断式（8）不适用于丘陵地区。相比而言，式（5）简洁、计算稳定性更好，适用性更强。

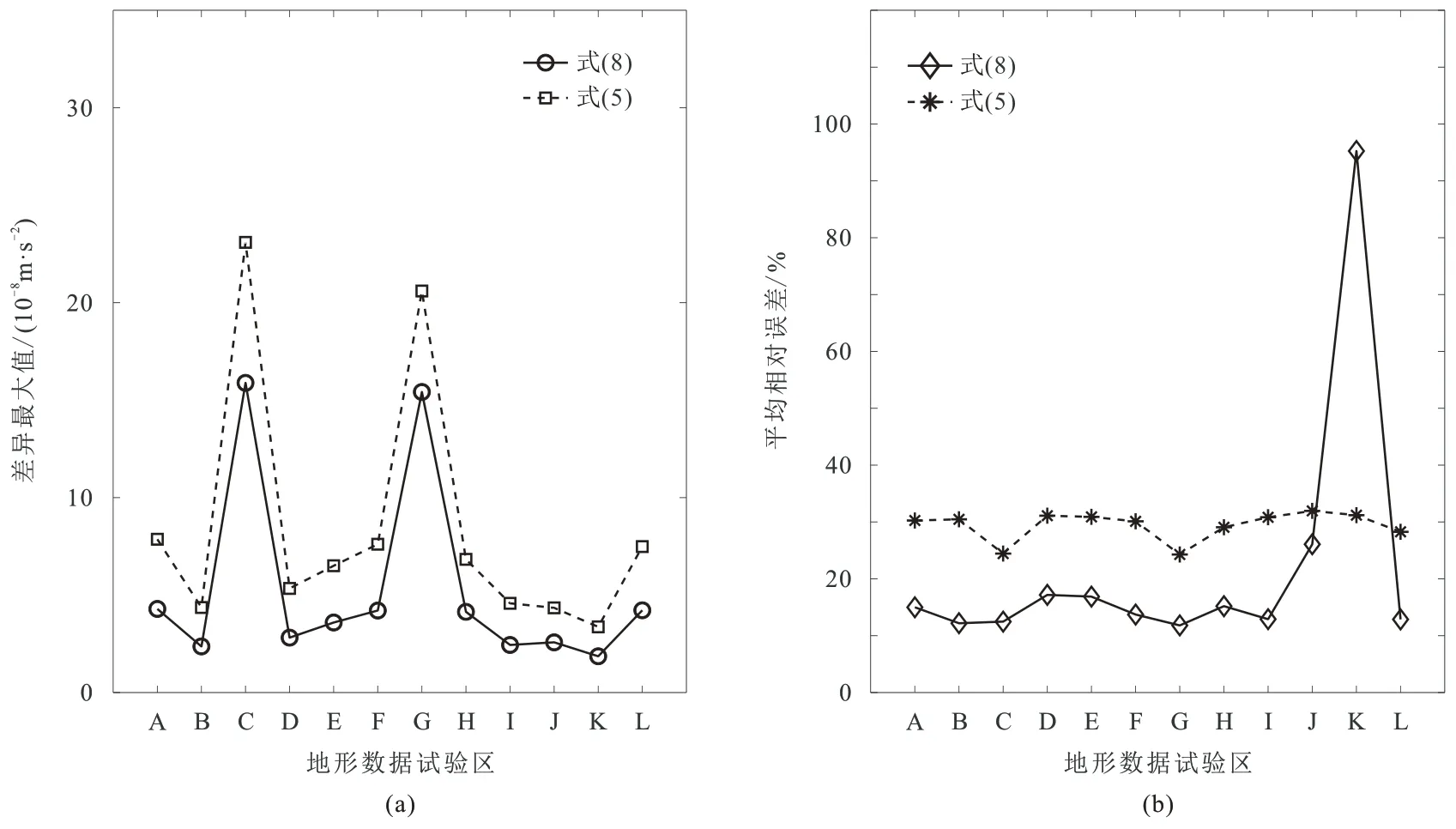
图8 内接口补角地形改正的差异最大值（a）及平均相对误差（b）

3.4 高程数据网格间距和计算方法对中区地形改正的影响

重力勘探中区地形改正主要分为圆域计算或方域计算，前者利用扇形柱体模型，多用于早期手工数据成图阶段或圆域电子量板地形改正，后者利用规则网格划分的直棱柱模型，便于计算机编程计算。当前，方域计算已成为主要方式。参考地质矿产行业标准［15］，区域重力调查中区地形改正范围一般为50～2000 m，而1∶5 万比例尺的重力中区地形改正范围则为20 ～2000 m。

对12 个试验区的原始1 m×1 m 高程数据进行粗网格化操作，分别得到5 m×5 m、10 m×10 m、20 m×20 m、40 m×40 m 以及50 m×50 m 共5 种网格间距的高程数据，对每个试验区分别采用直棱柱模型解析式法、质量线模型、梯形积分法以及三角面元高斯积分法进行计算，进而分析网格间距和计算方法对中区地形改正的影响。每个试验区平均分布间距为400 m 的256(16×16) 个测点，测点高程采用试验区相同水平位置的高程值。将粗网格处理得到的低分辨率DEM 的地形改正值与测点参考值的差异作为研究对象，即利用每个试验区的256 个测点的平均差异值评价四种计算方法的误差。为了简单起见，给出C 区、I 区、K 区和L 区的计算结果（图9）。可见：①不同网格间距计算结果差异较大。当网格间距为1 m×1 m 和5 m×5 m 时，四种计算方法的平均差异值均小于20×10-8m/s2，三角面元高斯积分法和质量线模型法均优于梯形积分法；当网格间距大于或等于20 m×20 m时，四种计算方法的平均差异值明显增大，不同计算方法的增幅不同。②K 区计算结果（图9c）的统计特征明显不同于其他区。C 区（图9a）、I 区（图9b）和L 区（图9d）的平均差异曲线趋势类似；当内边界为20（图9c 左）、50 m（图9c 右）时，K 区三角面元高斯积分法的平均差异值分别大于280×10-8、360×10-8m/s2，其他方法的平均差异值均小于15×10-8m/s2，说明三角面元高斯积分法不适用于丘陵区。③网格间距对不同计算方法的影响不同。随着网格间距增大，总体上平均差异值也增大，其中梯形积分法的平均差异值曲线斜率最小，说明该方法较稳定；当网格间距为1 m×1 m～20 m×20 m 时，三角面元高斯积分法的曲线斜率大于其他计算方法，说明该方法受网格间距的影响较大。④内边界从20 m（图9a 左～图9d 左）增大到50 m（图9a 右～图9d 右），平均差异值整体降低。当网格间距小于20 m×20 m时，图9a 右～图9d 右的平均差异值总体上与图9a左～图9d 左相同；当网格间距小于40 m×40 m 时，三角面元高斯积分法的计算精度与质量线模型法接近，且明显高于梯形积分法，说明三角面元高斯积分法受中区地形改正内边界的影响较大；网格间距由40 m×40 m 增大到50 m×50 m 时，平均差异值基本不变，说明内边界增至50 m 可降低网格间距对计算结果的影响。

直棱柱模型解析式法、梯形积分法、质量线模型法以及三角面元表面积分法的计算时间分别为457.93、48.69、57.87 和157.01 s，因此梯形积分法的计算效率最高，其中三角面元高斯积分法的计算时间和计算精度受高斯节点数量的影响（本文采用三个节点）。综合考虑计算效率和计算精度，认为质量线模型法可作为中区地形改正的首选方法，特别是当网格间距为5 m×5 m～20 m×20 m 时，该方法的平均差异值与直棱柱模型解析式法相近。

对试验区统一采用质量线模型法进行中区地形改正，得到平均差异值统计数据（图10）。可见：①当网格间距小于20 m×20 m时，无论中区地形改正范围内边界是20 m（图10a）还是50 m（图10b），平均差异值均小于20×10-8m/s2。②当内边界从20 m（图10a）增到50 m（图10b），平均差异值整体减小。③内边界为20 m、网格间距大于40 m×40 m 时（图10a），仅有D 区、E 区、H 区、G 区和K 区的平均差异值小于40×10-8m/s2，其他试验区的平均差异值较大，其中C 区的平均差异值大于100×10-8m/s2；内边界为50 m、网格间距大于40 m×40 m 时（图10b），C 区的平均差异值减小（小于60×10-8m/s2)。④内边界为50 m时（图10b），网格间距为40 m×40 m 与50 m×50 m的计算结果高度相近，因此内边界增大到一定程度可减弱网格间距对计算结果的影响。

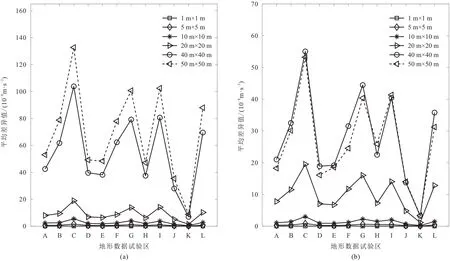
图10 由质量线模型法得到的地形改正范围分别为20～2000 m（a）、50～2000 m（b）的中区地形改正平均差异值

综上所述：为了保证高山区中区地形改正精度，应采用较高水平分辨率的DEM，并设定地形改正范围的内边界为50 m；采用网格间距为20 m×20 m 以及质量线模型方法可以获得较高的地形改正精度，并确保平均差异值小于20×10-8m/s2。

4 结论

本文基于包含美国典型地貌（喀斯喀特山脉、落基山脉、阿巴拉契亚山脉、德克萨斯丘陵、宾汉峡谷铜矿区）的1 m×1 m 激光雷达DEM，以直棱柱模型解析式计算结果为地形改正参考值，对比、分析了重力勘探近区和中区地形改正的模型近似误差和计算方法误差；基于5 种低分辨率网格高程数据和4 种计算方法，分析了网格间距、中区地形改正内边界和计算方法对中区地形改正的影响。得到如下认识。

（1）采用八方位圆域、方域等7种计算方案的近区地形改正统计结果表明，近区地形改正范围与计算模型是影响计算结果的主要因素。使用混合模型方案可有效降低模型近似的计算误差，当近区地形改正半径为20 m 时，采用混合模型的方案Ⅴ可以保证K 区以外的11 个区的平均相对误差小于20%；当近区地形改正半径为50 m 时，采用八方位方案Ⅶ可以将全区的平均相对误差控制在13%以内，是计算精度最高的方案。

（2）近区地形改正计算结果表明，地形起伏较平缓的丘陵（K 区）的差异最大值与中山（J 区）相当；在复杂地表的露天铜矿区（L区），7种计算方案的差异最大值大致处于相同量级。

（3）补角地形改正的修正公式（式（8））不适用于丘陵。相比而言，区域重力调查规范给出内接口补角地形改正的简化公式（式（5））的平均相对误差约为30%，表达式简洁、计算稳定性更好，适用性更强。

（4）影响中区地形改正计算结果的因素包括高程数据网格间距、中区地形改正内边界和计算方法，其中网格间距是主要因素。当网格间距小于20 m×20 m 时，质量线模型法地形改正结果的平均差异值均小于20×10-8m/s2，中区地形改正内边界明显影响三角面元高斯积分法的计算精度。

（5）当中区地形改正范围为50～2000 m 时，计算精度从高到低的排序为直棱柱模型解析式法、质量线模型法、三角面元高斯积分法、梯形积分法，计算时间分别为457.93、57.87、157.01、48.69 s。综合计算精度和计算时间两个因素，质量线模型法为首选计算方法。