纵波与横波反演能力对比

代福材，张峰*，钱忠平，孙鹏远，邹振，李向阳，3

（1. 中国石油大学（北京）油气资源与探测国家重点实验室，北京 102249；2. 中国石油大学（北京）CNPC 物探重点实验室，北京 102249；3. 东方地球物理公司，河北涿州 072750；4. 油气勘探计算机软件国家工程研究中心，北京 100088）

1 问题的提出

目前，油气地震勘探主要利用了纵波（PP 波）的信息。纵波对地层的声波速度、阻抗的变化最为敏感，在构造成像、断层解释等方面得到了广泛应用；结合岩石物理分析可以在一定程度上描述储层特征［1］、识别孔隙流体的变化［2-3］。油气藏的定量解释依赖于利用地震数据反演所获得的地层参数，而仅利用有限角度（炮检距）的纵波数据同步反演多个弹性参数比较困难［4-5］。其中，密度（ρ）反演尤为困难，这是因为纵波对密度的变化不敏感［6］。实例表明，为了准确反演地层密度，需要使用经过各向异性偏移成像、子波拉伸校正、吸收衰减补偿等处理的大角度（60°）纵波数据，同时还要保证初始模型可靠、正则化方法适用［7］，而在许多实际勘探工作中难以满足以上条件。虽然两参数（纵波阻抗和横波阻抗、AVO 截距和梯度等）反演方法比三参数（如纵波阻抗、横波阻抗、密度）反演更加可行，但是反演结果存在一定的误差和不确定性，这同时对数据和反演方法有着较高的要求［8-9］。此外，纵波在“气烟囱”成像、复杂和非常规油气藏的岩性识别、流体预测等方面也存在困难［10-11］。

相比于纵波，横波（SV-SV 波和SH-SH 波）的动力学特征有着显著的差异。在同一频带、相同的吸收衰减条件下，横波数据的分辨率更高，对地层的横波速度（VS）、密度、剪切模量、各向异性参数等更为敏感，因此可以用来更好地反演以上参数。如图1所示，相比纵波资料，横波资料在反演横波速度、密度等参数时不确定性更低，在描述油气藏的骨架性质、物性特征、裂缝、地应力等方面具有明显优势［12-16］。因此，将横波引入油气勘探能够弥补纵波勘探能力的不足，有助于提升复杂油气藏的储层预测精度和油气识别能力［17-19］。

图1 PP 波（a）与SH-SH 波（b）反演纵波速度、横波速度、密度的后验概率密度分布

为了明确横波的传播机理，诸多学者开展了理论研究［20-25］。横波曾在早期被应用于地震勘探［26-28］，通过多分量地震采集得到的横波各向异性属性用于裂缝油气储层描述［29-30］，但在较长的一段时期内，横波并没有在油气勘探中得到广泛应用，主要是因为传统的横波震源技术无法获得高品质数据。

转换横波不依赖于震源，可以通过爆炸源和垂直力源激发、三分量检波器接收，因此从20世纪90年代开始，它作为横波的替代应用于油气勘探。目前，业界已针对转换波数据的处理和成像开展了大量的研究工作［31-35］。实际应用结果表明，由于横波传播基本不受流体影响，转换横波在气云区成像方面具有一定的优势［36］；联合反演纵波和转换横波数据有助于改善地层横波速度和密度的反演结果，提高了反演稳定性和精度［37-39］。然而，相比纵波，转换横波的数据品质往往较低，难以独立应用于储层的精细描述。纵波和转换波联合反演的效果在很大程度上依赖于纵、横波数据的匹配精度，这导致联合反演方法在实际应用中受到一定程度的制约。

近年来，大吨位、宽频横波可控震源技术在油气勘探行业中迅速发展，可以激发与纵波数据品质相当的SV-SV 波和SH-SH 波［40-44］，为横波油气勘探技术的发展和广泛应用提供了良好的基础。但是，目前地震横波的反演理论尚不完善，有必要进一步开展纵波与横波的反演能力对比、分析，为横波反演方法研究提供理论依据。为此，本文首先介绍了不同类型地震波反射系数的近似式，并通过与精确反射系数对比分析近似式的精度；然后构建针对不同弹性参数的线性反演框架，计算不同待求参数组合的反演协方差矩阵，对比PP 波、PSV 波、PP 波和PSV波联合、SH-SH 波、SV-SV 波在反演不同弹性参数时的不确定性；进而通过计算不同类型地震波反演的特征值和条件数，对比、分析反演问题的不适定性；最后以反演协方差矩阵和反演条件数为依据明确了不同类型地震波的反演能力及横波反演方法的应用潜力。

2 不同类型地震波反射系数近似公式

不同弹性参数表示的反射系数近似式广泛应用于地震反演，因此在介绍PP 波、PSV 波、SH-SH 波、SV-SV 波反射系数近似式基础上，通过与精确反射系数对比分析其精度。

2.1 PP 波

PP波的反射系数近似式为［45-46］

根据弹性参数之间的关系，可得到利用纵波阻抗IP、横波阻抗IS等参数表示的近似式为［47］

利用IP、剪切模量μ等参数表示的近似式可表示为

对比PP 波反射系数近似式与精确公式，分析近似式在不同入射角的精度。采用的弹性界面参数如表1 所示，其中模型1 和模型2 均为弱阻抗差，模型3和模型4均为强阻抗差。

表1 不同模型弹性参数

由图2 可见，式（1）～式（3）的精度基本相同。在弱阻抗差情况下（图2a、图2b），反射系数近似式在入射角50°以内保持较高的精度；在强阻抗差情况下（图2c、图2d），虽然在临界角附近的精度有所下降，但在入射角30°以内依然保持较高的精度。由此可以得出结论，PP 波反射系数近似式可用于后续反演能力分析。

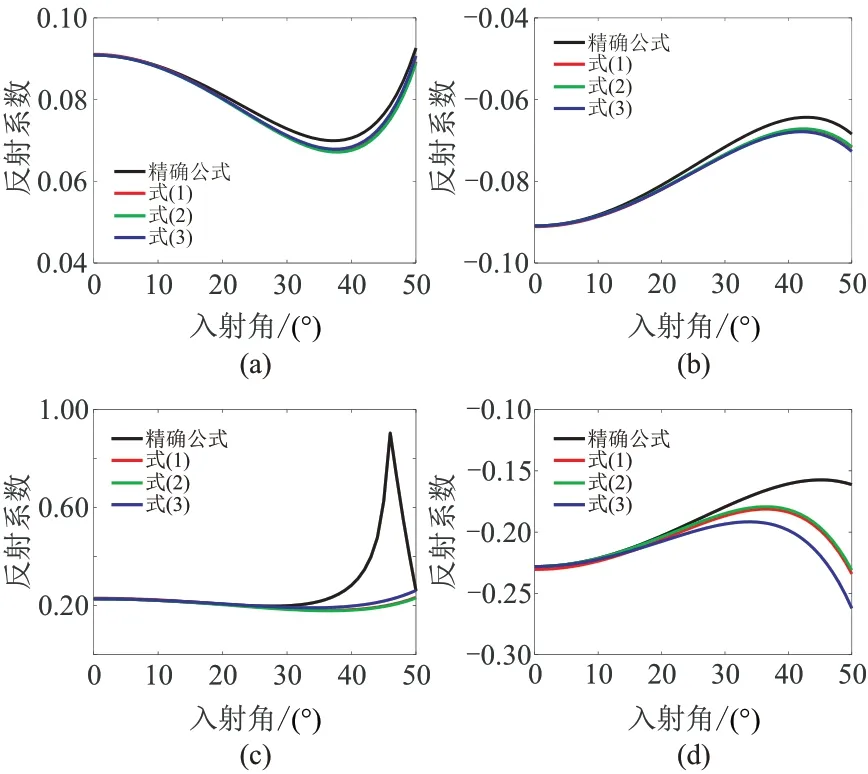
图2 PP 波反射系数近似式精度分析

2.2 PSV 波

PSV 波的反射系数近似式为［48］

式中θ和ϕ分别表示PP 波的入射角和PSV 波的反射角。

在此基础上，根据弹性参数之间的关系可进一步整理得到IS和ρ表示的近似式

利用μ和VS表示的近似公式为

从式（4）～式（6）可以看出，PSV 波的反射系数近似式虽然只含有2 个待反演的模型参数，但是由于公式中还包含了θ、ϕ、γ，因此实际上各个待求参数的系数并不是“参数独立”的。在实际反演时，反射系数公式中的系数项对待求参数的先验信息的依赖性较高。

对比PSV 波反射系数近似式与精确式，分析近似式在不同入射角的精度。同样采用表1所示的弹性参数。

由图3 可见，式（4）～式（6）的精度基本相同。在弱阻抗差情况下，反射系数近似式在入射角50°以内保持较高的精度；在强阻抗差情况下，虽然在临界角附近的精度有所下降，但在入射角30°以内仍然保持较高的精度。

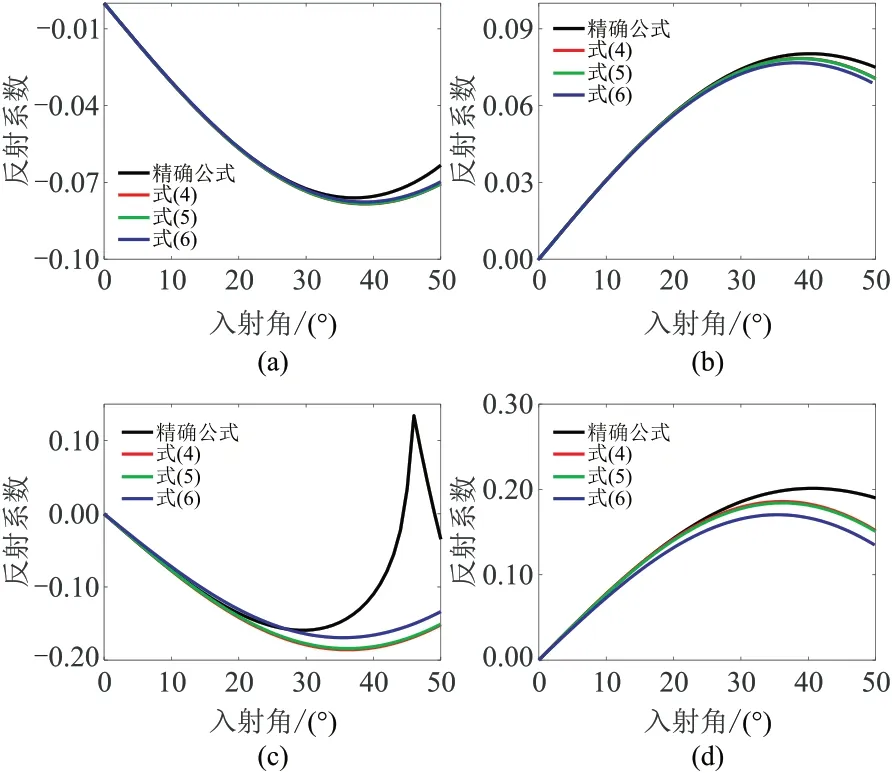
图3 PSV 波反射系数近似式精度分析

2.3 SH-SH 波

SH-SH 波反射系数的精确式可表示为［49］

式中ϕ1和ϕ2分别表示SH波的入射角和透射角。根据上式，SH波的反射特征仅与地下介质的2个参数（横波速度和密度）有关，这与PP波的反射特征有显著差异。

将式（8）代入式（7），忽略二阶以上高阶项，可推导出用VS和ρ表示的SH-SH波反射系数的近似式［50］

在此基础上，可进一步推导得到利用IS和VS表示的近似式

利用μ和VS表示的近似式为

从式（9）～式（11）可以看出，SH-SH 波的反射系数方程都具有非常简单的表达形式，即每个方程只含有2个待反演的模型参数（如式（9）中的VS和ρ），并且各个待求参数的系数是“参数无关的”，在实际反演时无需依赖待反演参数的先验信息。

对比SH-SH 波反射系数近似式与精确公式，分析近似式在不同入射角的精度，同样采用表1 所示的弹性参数。

由图4可见，式（9）～式（11）的精度基本相同。在弱阻抗差情况下，反射系数近似式在入射角50°以内保持较高的精度；在强阻抗差情况下，虽然由于临界角导致精度有所下降，但在入射角30°以内仍然保持较高的精度。

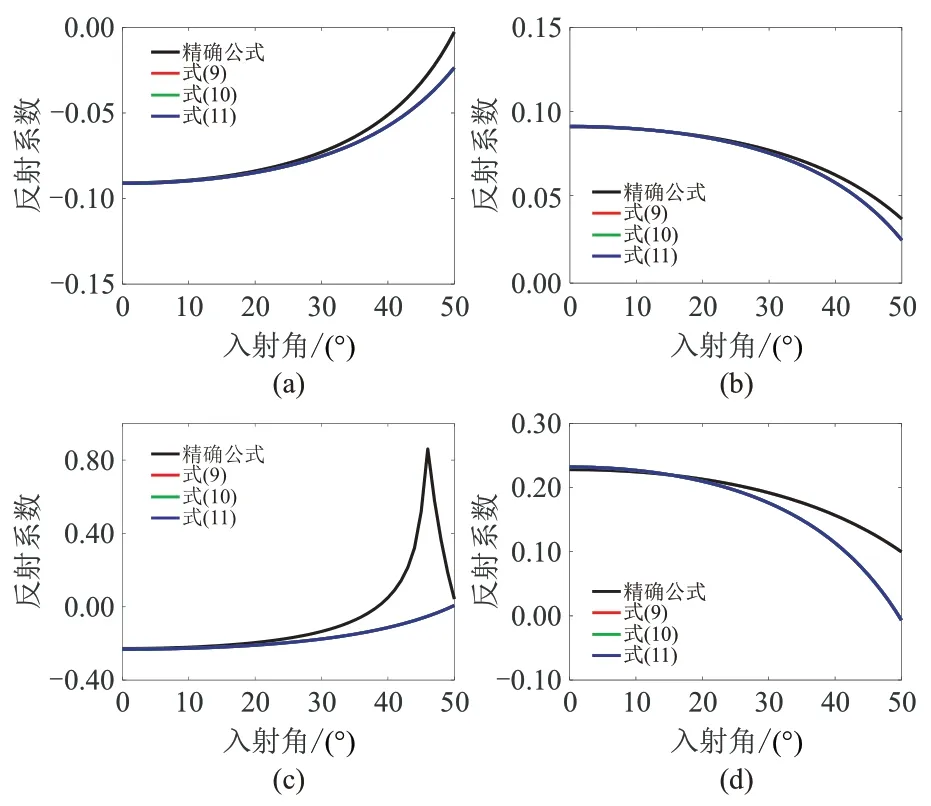
图4 SH-SH 波反射系数近似式精度分析

2.4 SV-SV 波

Zhang［51］推导了用VS和ρ表示的SV-SV 波反射系数的改进公式，即

式中为SV 波入射角和透射角的平均值。根据弹性参数之间的关系，可推导得到IS和VS表示的近似式

利用μ和VS表示的近似式可表示为

从式（12）～式（14）可以看出，SV-SV 波近似式中的与地层的横波速度有关，因此SV-SV 波反射系数近似式中各个待求参数的系数不仅与角度有关，同时也受介质VS的影响，并非完全“参数无关的”，并且SV-SV 波反射系数由于受纵波速度的隐性影响导致存在多个临界角。在VS2>VS1时，三个临界角分别为多临界角会导致近似式在临界角处出现较大误差。

对比SV-SV 波反射系数近似式与精确公式，分析近似式在不同入射角的精度，同样采用表1 所示的弹性参数。

由图5 可见，反射系数近似式式（12）～式（14）的近似精度基本相同。在弱阻抗差情况下，反射系数近似公式在入射角50°以内保持较高的精度；在强阻抗差情况下，多临界角现象导致近似式精度大幅下降（在模型3时，第一个临界角约为21°），仅在入射角20°以内保持较高精度。

图5 SV-SV 波反射系数近似式精度分析

综上所述，不同类型地震波反射系数近似式在弱阻抗差（模型1 和模型2）的情况下，入射角50°以内均保持较高的近似；在强阻抗差（模型3和模型4）的情况下，近似式的精度出现了不同程度的下降，这是由于近似式的推导是基于弱阻抗假设条件的。因此，在后续的反演分析中，本文采用的最大入射角为50°，反射系数近似式的精度可满足理论分析的需求。

3 基于协方差矩阵的反演不确定性分析

3.1 方法原理

根据不同类型地震波的反射系数近似式可以构建一个线性正演方程

式中R、F、m分别表示反射系数（观测数据）、正演算子（映射关系）、模型参数（待求参数）。

根据贝叶斯原理，待求参数的后验概率密度分布的最大值是其期望值，参数的方差可描述后验概率密度分布与期望之间的离散程度，因此方差可用于描述参数估计的不确定性。参数协方差矩阵的对角线元素表示每个参数估计的方差，而非对角元素表示不同变量之间的相关性，因此参数协方差矩阵可用于研究反演中的不确定性。本文采用Downton［8］和Zhang等［52］的方法，通过计算待求参数的协方差矩阵Cm，定量分析反演的不确定性。当数据噪声满足高斯分布，并且符合均匀、不相关的假设，则协方差矩阵Cm可通过下式计算

式中：σn为估算的数据噪声标准差；不同类型地震波的F矩阵具体形式见附录A。

利用不同弹性参数表示的反射系数近似式可得到对应的待求参数组合。本文分别计算了最大入射角度分别为30°、40°、50°时的反演协方差矩阵。协方差矩阵中某元素的数值越大，表明反演该元素对应的参数的不确定性越大。结合前人的研究成果，本文将反演协方差矩阵中元素值小于0.05 作为反演不确定性较小的定量评价标准。

3.2 结果分析

3.2.1 PP 波

PP波在不同最大角度下的反演协方差矩阵如图6所示。由图可见，对于所有的待求参数组合，反演协方差矩阵中各元素的数值都随着PP 波数据的最大入射角度的增加而减小，这表明入射角度越大，反演各个参数的不确定性越小。当PP 波数据的最大角度为30°时，只有IP的不确定性较小，而其他参数的不确定性都很高（图6a），这表明当使用小角度（<30°）的PP波数据反演其他参数时，反演结果的准确性在很大程度上依赖于数据的品质、初始模型的可靠性、正则化方法等。当PP 波数据的最大角度达到40°时，IS的不确定性明显降低，但是其他参数的不确定性仍然很高（图6b）。当PP 波数据的最大角度达到50°时，所有参数的不确定性都能够降低到相对理想的数值（各参数的协方差<0.05），但是ρ和μ的不确定性相比于纵、横波阻抗仍然较高（图6c中和图6c右）。因此，相比于其他参数，需要输入较大角度的数据（>50°），PP 波才可准确反演ρ和μ。

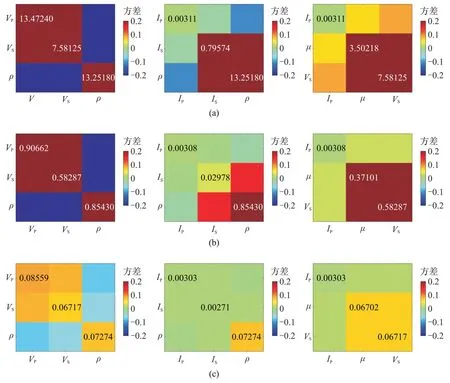
图6 不同角度数据PP 波反演不同弹性参数时的协方差矩阵

3.2.2 PSV 波

PSV 波在不同入射角下的协方差矩阵如图7 所示。由图可见，当PSV 波的最大角度为30°时，只有IS的不确定性较小，其他参数的不确定性都很高（图7a）；当最大角度达到40°时，各参数的不确定性明显降低（各参数的协方差<0.1， 图7b）；当最大角度达到50°时，所有参数的不确定性都非常低（各参数的协方差都接近0， 图7c）。以上角度均为纵波入射角，在纵、横波速度比为1.25 时，对应的横波反射角分别为23.6°、30.9°、37.8°。值得注意的是，相比于纵波数据，PSV 波数据品质相对较低，并且由于PSV波传播路径的不对称性导致其数据处理流程较为复杂，难以独立应用于精细的储层描述，一般应联合应用PSV 波和PP 波数据以提升反演稳定性和解释的精度。

3.2.3 PP 波和PSV 波联合反演

由于单独利用PP 波反演ρ、μ等参数会存在较大的不确定性，在实际应用中，通常加入PSV 波信息，利用PP-PSV 波联合反演以减少反演的不确定性。

根据PP 波和PSV 波近似式（式（1）～式（6）），PPPSV 波联合反演不同参数的不确定性如图8 所示。由图可见，当最大角度（纵波入射角）为30°时，IP和IS的不确定性较小，其他参数的不确定性相比PP 波反演有所下降，但仍然较高（图8a）；当最大角度达到40°时，各参数的不确定性明显降低（各参数的协方差<0.05，图8b）；当最大角度达到50°时，所有参数的不确定性都非常低（各个参数的协方差都接近0，图8c）。在纵、横波速度比为1.25 时，对应的横波反射角分别为23.6°、30.9°、37.8°。结果表明：相较于单独使用PP 波，联合使用PP 波和PSV 波在反演ρ和μ等参数时具有明显优势。PSV 波数据的处理过程比纯波（PP 波、SV-SV 波、SH-SH 波）更为复杂，因此在实际应用中，联合反演的效果很大程度上依赖于纵、横波数据的匹配精度，而实际上地震纵、横波数据的高精度匹配仍然存在一定的困难。

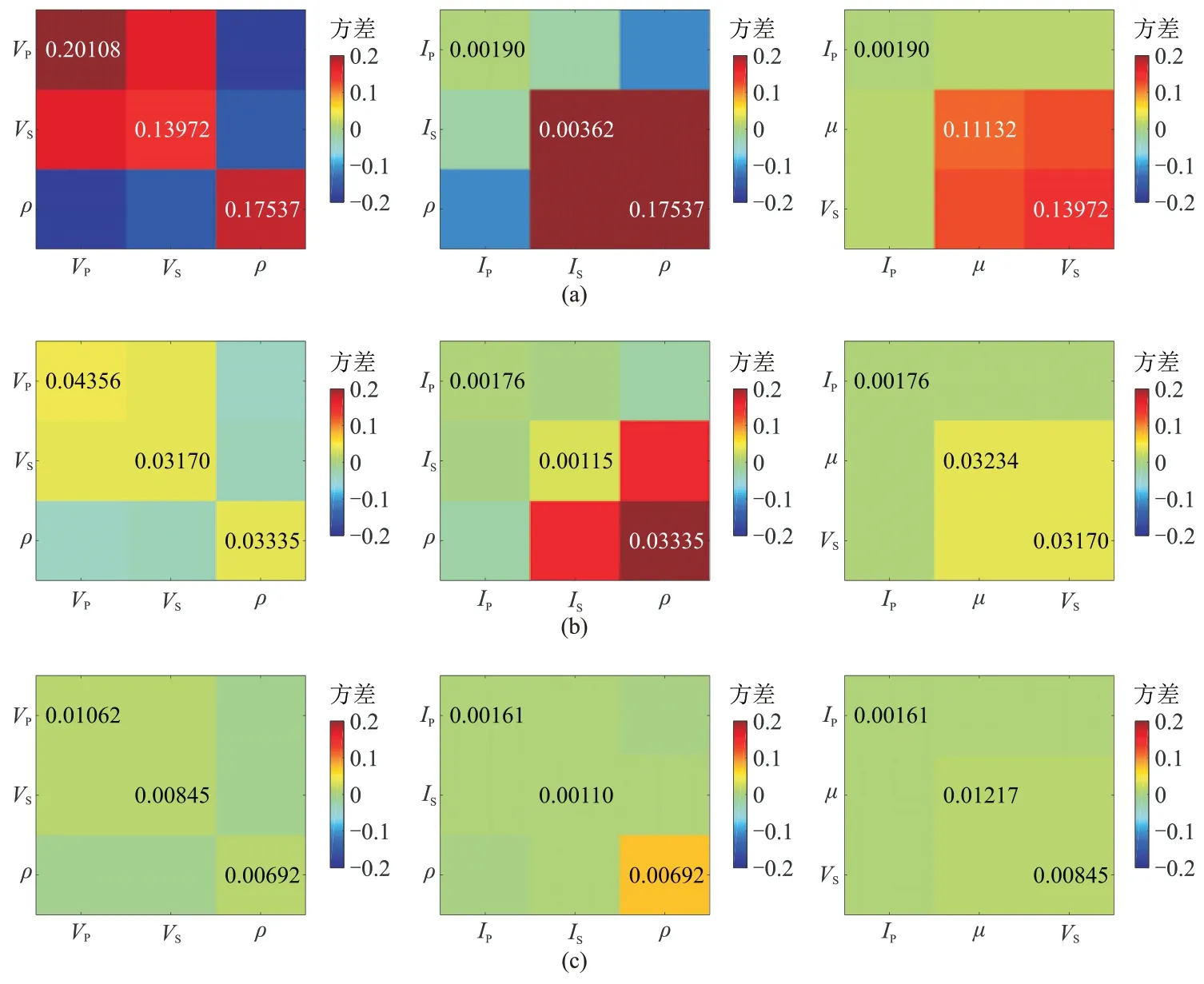
图8 不同角度PP 波和PSV 波联合反演不同弹性参数时的协方差矩阵

3.2.4 SH-SH 波

SH-SH波反演不同弹性参数的不确定性如图9所示。由图可见，即使使用小角度的数据（<30°），SH-SH波反演IS、VS、ρ、μ的不确定性也较小（图9a），参数协方差的数值基本与PP 波最大入射角为50°时的反演结果相当。当SH-SH 波数据的最大角度达到40°时，各参数的不确定性进一步降低（各参数协方差<0.05，图9b）；当最大角度达到50°时，反演的不确定性已经非常小（各参数的协方差接近0，图9c）。相比于PP波，SH-SH 波在反演ρ和μ等参数时具有明显的优势。此外，SH-SH 波的反射系数近似式中各个待求参数的系数是“参数无关的”。在实际反演时，SH-SH 波相比于PP 波和PSV 波（待求参数的系数与γ有关）对待求参数的先验信息的依赖更小，并且SH-SH 波仅包含两项待反演参数，因此可有效减少反演的病态性，提高反演的稳定性。

图9 不同角度SH-SH 波反演不同弹性参数时的协方差矩阵

3.2.5 SV-SV 波

SV-SV 波的反演协方差矩阵如图10所示。由图可见，与PP 波相比，SV-SV 波在反演IS、VS、ρ、μ等参数时的不确定显著降低。仅使用小角度（<30°）的SVSV 波数据即可稳定反演各个参数（各参数协方差<0.05， 图10a），更大角度的数据对待求参数的不确定性的影响较小（图10b、图10c）。因此，相比于SH-SH波，SV-SV 波在反演不同弹性参数时对输入数据的最大角度的需求更低。值得注意的是，SV-SV 波与SHSH 波虽同属横波，在各向同性介质中两者具有相同的传播速度，但是SV-SV 波与PP 波的偏振方向在同一平面，SH-SH 波的偏振方向垂直于前两者所在的平面。因此，在实际数据的波场分离中，SV 波更容易受到P 波的影响［53］，而SH 波则与PP 波完全解耦，并且SV-SV 波存在多临界角现象。因此，关于SV-SV 波反演和SH-SH 波反演的适用性需要结合实际数据具体分析。

图10 不同角度SV-SV 波反演不同弹性参数时的协方差矩阵

综上所述，对于同一类型地震波的不同待求参数组合，反演的不确定性也存在一定差异。PP 波及PP波与PSV 波联合反演的最佳待求参数组合为IP、IS和ρ；PSV 波的最佳待求参数为IS和ρ；SV-SV 波和SHSH 波的最佳待求参数为IS和VS。地震横波（SH-SH波和SV-SV 波）在反演μ、ρ等参数时，相较于PP 波和PSV 波在反演能力和反演精度等方面有了显著的提升。除此之外，地震横波的数据处理流程与纵波类似，相较于转换横波的处理流程而言已大幅简化，并且反演结果不依赖于高精度的纵、横波数据匹配，因此在油气储层精细描述中具有很大的应用潜力。

4 基于特征值和条件数的反演不适定性分析

4.1 方法原理

在数据空间和模型空间可以将F奇异值分解（Singular Value Decomposition，SVD）为三个正交分量［54］

式中：Λ为特征值的对角矩阵；M表示模型空间的特征向量；D表示数据空间的特征向量（图11）。特征值表示对应分量的能量，特征值越大表示模型参数对应的能量分量越大。如果不同参数的特征值相差较大，表示反演结果具有较强的病态性，需要大角度信息才可准确反演模型参数。因此，可根据不同角度的特征值分析反演的不适定性。

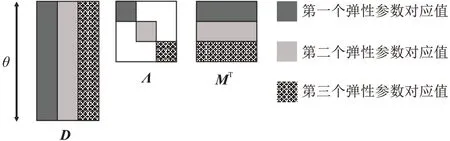
图11 线性正演算子奇异值分解示意图［54］

通常可以用条件数描述反演的不适定性，它为F的范数与F的逆的范数的乘积，即

对于反演而言，条件数较大的反演称为病态，条件数较小的反演称为良态。因此，可进一步利用条件数随最大入射角的变化分析线性反演的不适定性。为便于直观显示，本文将特征值和条件数的单位均用dB（即20 lgλi，λi表示特征值）表示。由于条件数可表示为最大特征值与最小特征值的比值，在对数形式下，条件数即为最大特征值与最小特征值之差。

4.2 结果分析

根据不同反射系数近似式构建F，并对F进行奇异值分解可分析线性反演的不适定性。为了与前文近似精度分析保持一致，选择最大入射角为50°，并将反演条件数小于20 dB 作为反演不适定性较小的定量评价标准，即弹性参数对应能量分量最大值与最小值相差10倍。

4.2.1 PP 波

根据PP 波反射系数近似式（式（1））构建F，计算得到的特征值及条件数随最大入射角的变化情况如图12 所示。由图可见，VP特征值随最大入射角变化较小，并且在三个特征值中一直最大，表示VP对应的能量分量最大；而ρ特征值最小，表示ρ对应的能量分量最小。虽然ρ特征值随最大入射角增大而增大，但在最大角度为50° 时，ρ特征值与VP特征值仍相差30 dB 左右（图中红点处），这表明即使在大角度情况下密度参数仍然难以准确反演。不同参数之间的特征值差异随着最大入射角的增大而减小，对应的反演条件数随最大入射角的增大而减小，但在最大角度为50° 时，反演条件数仍然较高（大于20 dB），这表明PP 波三参数反演具有较高的病态性，尤其是难以准确反演密度参数。

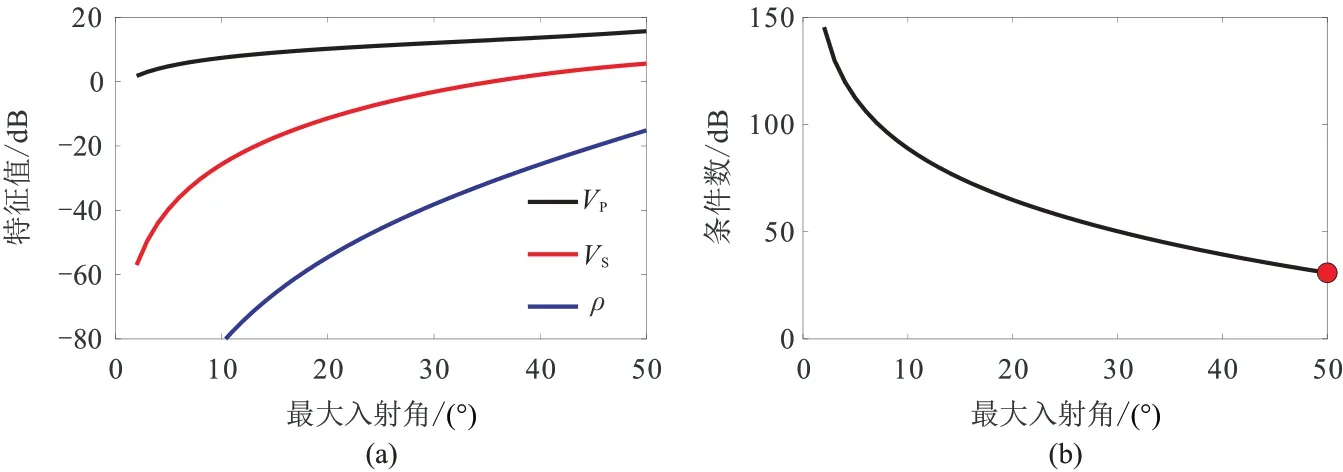
图12 PP 波反演的特征值（a）和条件数（b）随最大入射角的变化关系

4.2.2 PSV 波

PSV 波反演的特征值及条件数随最大入射角的变化情况如图13 所示，PSV 波反演仅有2 个待反演参数，其中VS特征值较大，表示VS对应的能量分量最大；而ρ特征值较小，随着最大入射角的增大，ρ特征值逐渐增大，并且在最大入射角为48° 左右时，ρ特征值与VS特征值之差下降到20 dB 左右（图中红点处），表明此时可以得到密度参数可靠反演结果。相比于PP 波三参数反演，PSV 波反演的条件数有所下降，在最大入射角为48° 时下降到20 dB 左右，表示PSV 波反演可在一定程度上降低反演的不适定性，但仍需45° 以上的中角度数据才可得到可靠的密度反演结果。

图13 PSV 波反演的特征值（a）和条件数（b）随最大入射角的变化关系

4.2.3 PP 波和PSV 波联合反演

PP波和PSV 波联合反演的特征值及条件数随最大入射角的变化情况如图14 所示。由图可见，在三个特征值中VP特征值最大，表示VP对应的能量分量最大；而ρ特征值相比于PP 波反演明显增大，表示ρ对应的能量分量得到提高，因此ρ反演的稳定性得到显著提升。VP与ρ之间的特征值差异随着最大入射角的增大而减小，对应的反演条件数随最大入射角的增大而减小，这表明反演的病态性逐渐减弱。在最大入射角为20° 左右时，反演条件数下降到20 dB 左右（图中红点处），表明相比于PP 波三参数反演，PP 波和PSV 波联合反演可显著降低反演的不适定性，仅需20°左右的小角度数据即可准确反演密度参数。联合反演可有效提高反演的稳定性，但在实际应用中需要考虑纵、横波匹配精度的影响。

图14 PP 波和PSV 波联合反演的特征值（a）和条件数（b）随最大入射角的变化关系

4.2.4 SH-SH 波

SH-SH 反演的特征值及条件数随最大入射角的变化情况如图15 所示。与PSV 波类似，SH-SH 波反演仅有2 个待反演参数，其中VS特征值较大，并且一直大于0，表示VS对应的能量分量最大；而ρ特征值较小，随着最大入射角的增大，ρ特征值逐渐增大。在最大入射角为35°时，两者特征值之差下降至20 dB 左右（图中红点处），表明ρ的可靠反演仅需35°左右的中角度数据即可。相比于PP 波三参数反演，SH-SH 波反演的条件数大幅下降，表示SH-SH 波反演可有效降低反演的不适定性，在密度反演方面具有较好的应用潜力。

图15 SH-SH 波反演的特征值（a）和条件数（b）随最大入射角的变化关系

4.2.5 SV-SV 波

SV-SV 波反演的特征值及条件数随最大入射角的变化情况如图16 所示。SV-SV 波反演仅有2 个待反演参数，其中VS特征值随最大入射角变化较小，但数值一直大于0，说明VS对应的大部分反射波能量分量；而ρ特征值随着最大入射角的增大也明显增大。两者特征值之差在最大入射角为20°左右达到20 dB左右（图中红点处），表明ρ的可靠反演仅需20°左右的小角度数据即可。相比于PP 波三参数反演，SV-SV波反演的条件数大幅下降，表明SV-SV 波两参数反演具有较低的不适定性，在密度反演方面具有显著优势。

图16 SV-SV 波反演的特征值（a）和条件数（b）随最大入射角的变化关系

5 结果

综上所述，根据反演协方差矩阵和反演条件数可得到不同类型地震波反演弹性参数的反演能力如表2所示。从表中可以看出，横波（SV-SV 波和SH-SH波）在反演等横波阻抗IS、横波速度VS、剪切模量μ、密度ρ等参数时较纵波和转换横波有明显的优势，有效降低了反演对输入数据的需求，并且显著降低了反演的不适定性。

表2 不同类型地震波反演弹性参数时的可行性分析

6 结论与讨论

本文基于不同类型地震波反射系数近似式，构建线性反演框架，利用反演协方差矩阵和反演条件数对比、分析了地震纵、横波对不同弹性参数的反演能力。理论分析验证了横波在反演密度、剪切模量、横波速度等参数方面具有良好的应用潜力，可为横波反演方法研究提供有力的理论支撑。与转换横波相比，横波的处理过程更为简单，在弹性参数反演及储层预测方面具有良好的应用前景。

需要说明的是，以上理论分析并没有引入正则化，这是因为不同的正则化方法会不同程度地降低反演结果的不确定性和不适定性，不利于客观地分析不同类型地震波的反演能力。而在实际地震数据反演中，则需要合理使用正则化以降低反演结果的不确定性。另外，在分析中假设不同类型的地震波数据具有相同的信噪比，这一假设可能与应用中的实际情况并不一致。

附录A 不同类型地震波的线性正演算子F 表达式

根据P P波反射系数近似式（1），待求解参数为纵波速度VP、横波速度VS和密度ρ时，入射角度分别为θ1，θ2，…，θN（N为角度个数），P P波线性正演算子F可表示为

式中γ为纵横波速度比。

根据PSV 波反射系数近似式（式（4）），待求解参数为Vs 和ρ时，入射角度分别为θ1，θ2，…，θN，对应的SV 波反射角度为ϕ1，ϕ2，…，ϕN，F可表示为

根据SH-SH 波反射系数近似式（9），待求解参数为Vs 和ρ时，SH 波入射角度分别为ϕ1，ϕ2，…，ϕN，F可表示为

根据SV-SV 波反射系数近似式（式（12）），待求解参数为Vs 和ρ时，SV 波入射角和透射角的平均值分别为可表示为

当待求解参数为其他弹性参数时，根据不同类型地震波的反射系数近似式即可得到对应的F的表达式。