多年冻土区高寒草甸蒸散发模型适用性评价——以青藏高原风火山地区为例

肖锦旺， 王根绪， 胡兆永， 郭林茂， 李金龙

（四川大学 水利水电学院 山区河流保护与治理全国重点实验室，四川 成都 610065）

0 引言

青藏高原被称为地球的“第三极”［1］，拥有世界上海拔最高，分布最广的冻土层，是对气候变化最敏感的地区之一［2］。在全球变暖背景下，青藏高原气温显著升高，其速率约为北半球同纬度地区的两倍［3］。气温升高将改变地表的潜热和感热通量，并在一定程度上对区域的水文循环产生影响。蒸散发（ET）是水文循环的重要过程之一，是理解土壤-植被-气候相互作用的主要变量［4］。活动层厚度的增加、土壤温度的升高以及植被覆盖率［5］的增加将增大土壤蒸散发，进而影响区域水热平衡［6］。由于蒸散发量大小取决于气象因素（太阳辐射、气温以及湿度等）、下垫面植被以及土壤类型［7］，直接测得蒸散发十分困难。目前对于青藏高原蒸散发监测主要集中在季节冻土区［8］，然而对于广泛分布的多年冻土区蒸散发监测极其有限［9］，Ge 等［10］指出与季节冻土相比，多年冻土活动层的冻融循环对地表能量分布影响更大。因此，开展对青藏高原典型多年冻土区不同冻融阶段蒸散发模拟研究十分有必要。

蒸散发模拟研究方法主要分为以下3 类：辐射法（Priestley and Taylor［11］，PT 模型等）、综合法（Penman-Monteit［12］，PM 模型等）、互补理论法（Advection-aridity［13］，AA 模型、Generalized Nonlinear Complementary Principle［14］，CR 模型等）。上述三种方法在结构、复杂程度上以及所需的数据各不相同，对于不同下垫面的适应性有所差异。综合法所需的参数最多，包括空气动力学阻力、冠层边界层阻抗、叶面积指数和土壤信息［12］，而辐射法和互补理论法只需常规气象数据。综合法相比于其他方法，其对不同的下垫面适应性较强，但数据的获取难度大。联合国粮食和农业组织已将综合法FAO-Penman-Monteit（FAO-PM）模型作为计算蒸散发的标准模型［15-16］。辐射法PT 模型最开始应用于在最小平流的条件计算湿润表面的蒸散发［17-19］，是PM 模型的简化形式。αPT为Priestley-Taylor 校准系数，该系数表示实际蒸散发速率与平衡蒸散发速率的比值［17］，其值的大小会对模型性能产生直接影响，目前已有部分研究根据实际观测数据对青藏高原αPT值重新标定［20-21］。互补理论法包括线性互补理论法和非线性互补理论法，1979 年Bouchet 和Stricker［13］首次提出平流-干旱互补理论AA 模型（线性互补理论法），但是，Crago 等［22］和Qualls 等［23］指出在极端情况下AA 模型模拟的结果会发生偏差，极端湿润情况下会高估蒸散发，极端干燥情况下会低估蒸散发。2015 年Brutsaert 提出了广义非线性互补理论模型CR 模型，Wang 等［20］在原始CR 模型的基础上，将土壤冻融过程中冰水相变所消耗的潜热考虑在内，提出CRice，更适用于冻土地区的实际蒸散发模拟。已有研究使用上述3类模型分别对青藏高原典型多年冻土区蒸散发进行研究［24-26］，但由于不同方法的物理基础以及需要的数据支撑条件不同，其模拟计算结果也不尽相同，存在一定的源于方法本身的不确定性，因此，迫切需要进行不同方法的综合比较的研究，以明确不同方法的适用性和实际蒸散发的模拟能力。

为此，本文以青藏高原多年冻土区高寒草甸为研究对象，基于涡度相关法获得实际蒸散发数据，评价FAO-PM 模型、PT 模型、AA 模型以及CRice模型在该地区不同时间尺度蒸散发模拟的适用性，明确青藏高原多年冻土区高寒草甸蒸散发模拟的最优方案，为青藏高原多年冻土区水资源开发与利用提供一定理论基础。

1 材料和方法

1.1 研究区域概况

研究区位于青藏高原腹地北麓河一级支流左冒西孔曲风火山流域内（93°02′～92°50′ E、34°40′～34°47′ N），该区域是典型的多年冻土区（图1）。2014 年在该区域的高寒草甸安装一套涡度通量系统（主要包括红外气体分析仪（Li-7500A，LiCor，美国）和三维超声风速仪（Windmaster Pro，Gill，英国）及气象观测系统。研究区域海拔4 603～5 403 m，年平均气温为-5.2 ℃，年平均降水为290.9 mm，但年平均蒸发量高达1 316.9 mm，年平均相对湿度为57%，多年冻土厚度为50～120 m，活动层厚度变化范围为0.8～2.5 m［27］。研究区域植被以高寒草甸为主，高寒草甸植被群落以高山嵩草、矮嵩草和线叶草为主［27］。

图1 研究区概况Fig. 1 Overview of the study area： the location of fenghuoshan （a）； the temperature and humidity probe and the flux tower （b）；the location of the temperature and humidity observation point and the flux tower （c）

1.2 数据来源与处理

研究区架有自动气象站（92° 53.34′ E、34°43.07′ N，海拔4 809 m），其主要监测气温（℃）、相对湿度（%）、2 m 处风速（m·s-1）、净辐射（W·m-2）与土壤热通量（W·m-2）。在气象站旁安装高2 m 的涡度协方差系统监测潜热（W·m-2）和感染通量（W·m-2），该系统由三维超声波风速仪和红外气体分析组成。土壤温度由温湿度探头（92°53.78′ E、34°42.87′ N，海拔4 822 m）监测获得，其中土壤温度测量精度±1 ℃，分辨率为0.1 ℃，测量范围-40～60 ℃，适用于多年冻土区温度观测；土壤水分测量精度为±0.03 m3·m-3，分辨率为0.000 8 m3·m-3。

1.2.1 土壤温度数据处理

分别在土壤5 cm、20 cm、50 cm、160 cm 深度布设温湿度探头，温湿度探头每4小时监测一次数据，剔除较大离群值后将4小时土壤温度数据转换成日平均数据。本文根据2019—2020 年5～120 cm 土壤温度日变化（图2），将冻融过程划分为4 个时期：融化期（4 月20 日—5 月27 日，Tsoi5＞0.1 ℃）、完全融化期（5 月28 日—10 月17 日，Tsoil120＞0.1 ℃）、冻结期（10 月18 日—12 月8 日，Tsoil5＜-0.1 ℃）以及完全冻结期（12月8日—4月19日，Tsoil120＜-0.1 ℃）。

图2 2019—2020年5～120 cm土壤温度等值线Fig. 2 The 5～120 cm soil temperature contour from 2019 to 2020

1.2.2 涡度相关通量数据处理

使用EddyPro 软件（LI-COR， USA）对涡度相关数据进行预处理，包括尖波计数和去除［28］，H2O/CO2相对于垂直风分量的滞后修正、平面拟合坐标旋转［29］和WPL 密度波动修正［30］。过滤夜间负湍流通量以及较大的离群数据后（剔除的数据占总数据的17%），将半小时的涡度数据转换成日平均数据。能量闭合度是评价涡度数据的重要指标，通过对研究时段内风火山观测点能量通量数据进行闭合度分析，能量闭合度为0.75，Zhu 等［31］对中国通量网8 个站点的研究发现能量闭合度在0.58 至1.00 之间变化，通常情况下能量闭合度的可接受范围在0.7～0.9，因此说明本研究中使用的观测数据是可靠的。

1.2.3 气象数据处理

气象数据（气温、风速、湿度）每30 min 记录一次，剔除较大离群值后将半小时数据转换成日平均数据，同时筛选出每日最高气温和最低气温并将其单独列出。

1.3 蒸散发模型

本研究中选择基于综合法的FAO-PM 模型、基于辐射法的PT模型，以及基于互补理论法的线性模型AA 和改进的非线性关系模型CRice，模拟青藏高原典型多年冻土区风火山2016年4月—2017年4月以及2019 年4 月—2020 年4 月蒸散发。4 种模型的输入参数见表1。

表1 模型驱动变量Table 1 Model driving variables

1.3.1 FAO-Penman-Monteith模型

FAO-Penman-Monteith模型是1998年由联合国粮农组织（FAO）提出的计算潜在蒸散发的标准模型［15］，考虑了空气动力学阻力、冠层边界层阻抗、叶面积指数和土壤水分状况等因素对蒸散发的影响。FAO-Penman-Monteith方法的公式如下：

式中：ETFPM为潜在蒸散发量（mm）；Rn为地面净辐射（MJ·m-3·d-1）；G为土壤热通量（MJ·m-3·d-1）；γ为湿度计常数（kPa·℃-1）；U2为2 m高处的风速（m·s-1）；es为饱和水汽压（kPa）；ea为实际水汽压（kPa）；Tmean为2 m高度的平均气温（℃）；Δ为饱和水汽压温度曲线上的斜率（kPa·℃-1）。

1.3.2 Priestley and Taylor模型

Priestley and Taylor 模型［11］是Penman-Monteith模型的简化方法，只需要常规的气象数据就能计算蒸散发，计算公式如下：

式中：αPT为校准值常数，使用2015 年监测数据进行αPT标定，标定结果为1.18；Qne是以蒸发单位表示的可用能量（mm），Qne= (Rn-G)λ，λ为汽化潜热（kJ·kg-1）。

1.3.3 AA模型

基于实际蒸散发与潜在蒸散发之间的反馈，Bouchet 和Stricker 提出平流-干旱模型［13］（Advection-aridity，AA），该模型认为处于潮湿环境下（水分充足），蒸散发接近潜在值；干燥环境下，用于蒸发的能量变成产生感热通量。AA模型的公式如下：

式中：ρ为水的密度（kg·m-3），ra为空气动力学阻力（s·m-1）。ra可由式（4）求得：

式中：κ为von karman 常数，取值0.41；z1为风速观测高度（m）；z2为气温和湿度的观测高度（m）；本文z1和z2均取值2 m；d0为零平面位移可近似为2h3，h为植被高度。zom为动力学粗糙度（m），可近似等于h8；zov为水汽传输粗糙度（m），zov可近似等于0.1zom。

1.3.4 CRice模型

Brutsaert在严格的物理边界条件下重新定义了互补理论中的蒸散发相关变量的概念，提出了广义非线性互补理论模型（Generalized Complementary Relationship，CR［14］）。其公式如下：

式中：ETpo为潜在蒸散发（mm），ETpo可由Priestley and Taylor 等式求得；ETpa为表观潜在蒸散发，可用如下Penman-Monteith［12］公式：

式中：Qne=（Rn-G）/λ，f(ur)为风函数，风函数的计算选择roma公式［12］，其公式如下：

原始的CR 模型并未考虑多年冻土区冻结期间冰相变（Qice）所消耗的能量。Wang等［20］认为在冻结期土壤热通量G不能作为单一的能量消耗项，Qice所消耗的能量不能忽略，优化了非线性互补关系在冻土区的应用，提出了含冰能耗项的CRice模型，具体改进方法见Wang［20］等。

1.3 模型评价方法

模型评价采用确定系数（coefficient of determination，R2）、均方根误差（root mean squared error，RMSE）、平均误差（mean error， ME）以及纳什效率系数（Nash-Sutcliffe efficiency coefficient， NSE）。R2反映模型模拟值与实测值的拟合程度，ME 反映估算值和观测值之间的偏差，RMSE 可反映模型的绝对无偏性和极值效应，NSE 一般用来平均水文模型的模拟结果的好坏。通常情况下模型模拟结果的R2和NSE 越接近于1，ME 和RMSE 越接近0，模型的适用性越好。评价指标的计算方法见表2。

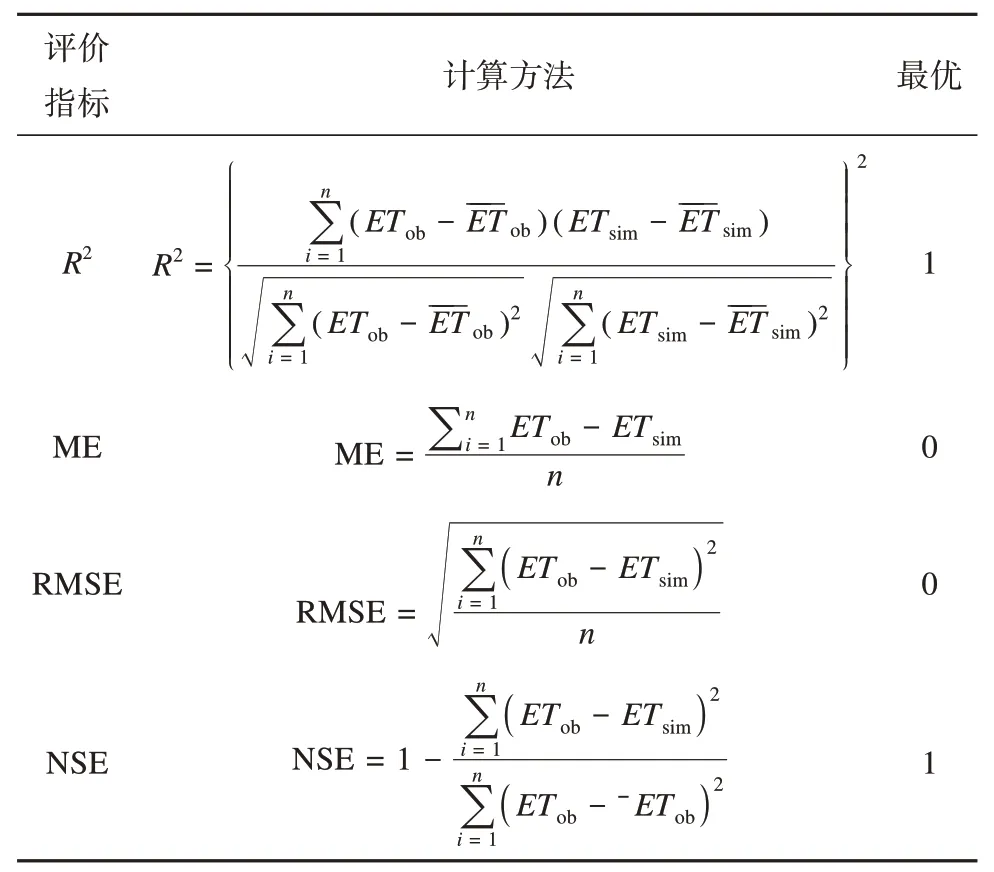
表2 模型评价指标Table 2 Model-evaluation index

2 结果与分析

2.1 风火山地表能量和气候特征

本文选用2019年4月—2020年4月监测数据对风火山地表能量和气候特征进行分析。图3为风火山监测站的气温、降水量、风速、相对湿度及地表能量通量（净辐射、感热、潜热和地表土壤热通量）的逐日变化特征。研究区日均最高气温为9.8 ℃，日均最低气温为-22.8 ℃。年最大气温差达到32.6 ℃；年降雨量为385 mm，降雨与气温具有明显的季节变化，呈现雨热同期，5—10 月气温高降雨量大，其余时间段气温低，降雨十分稀少。近地层风速冬季，最大日均风速达10 m·s-1，夏季日均风速一般低于4.5 m·s-1。受冬季低温影响，饱和水汽压较小，相对湿度较大，多在80%以上，夏季则相对较低。地表能量分配具有明显的季节性，冬季感热通量大于潜热通量，潜热通量变化幅度趋于平缓；夏季时，随着降雨的增加以及冻土的融化，地表含水量增加，潜热通量上升并超过感热通量，成为地气间能量交换的主导能量，同时波动程度大于冬季，地表热通量年内变化幅度较小。

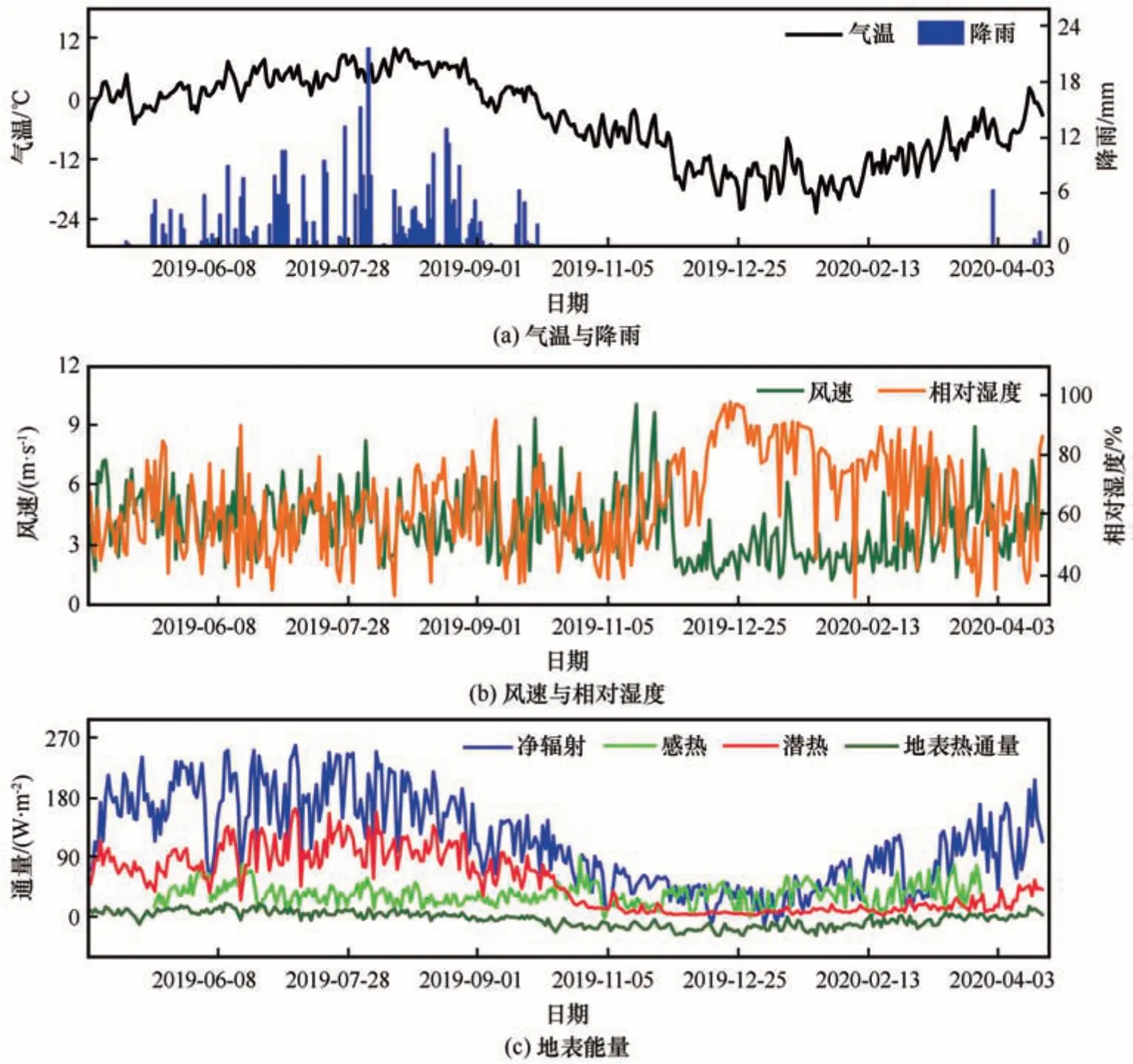
图3 2019年4月20日—2020年4月20日风火山主要气象要素和地表能量日变化Fig. 3 Daily variations of meteorological and surface energy flux at Fenghuoshan during 2019-04-20—2020-04-20

年内蒸散发变化的趋势总体呈现先增后减，融化期实际蒸散发波动性要大，冻结期的实际蒸散发较为平缓（图4）。随着气温升高，土壤表层以及地表积雪融化，融化期蒸散发量迅速增加，日平均蒸散发量达2.5 mm·d-1；在完全融化期，表层土壤逐渐向下融化，土壤水含量增加；同时伴随着雨季的到来，净辐射的增加，土壤蒸发以及植被蒸腾达到全年最大值，这一阶段日均蒸散发量约为2.5 mm·d-1，蒸散发总量约为386.4 mm，约占全年的69.8%；在冻结期，土壤开始双向冻结，土壤中液态水含量迅速减少，同时雨季结束，降雨量减少，蒸散发量迅速减少，日平均蒸散发量约为0.7 mm·d-1。完全冻结期土壤完全冻结，降雨几乎为0，地表蒸散发量处于全年最低值，日平均蒸散发量约为0.6 mm·d-1。

图4 2019年4月20日—2020年4月20日实际观测蒸散发Fig. 4 Observated evaporation during 2019-04-20—2020-04-20

2.2 年尺度的模型评价

由于2017 年5 月—2018 年8 月缺测，本文选用2016年4月—2017年4月以及2019年4月—2020年4 月数据进行模型评价。由图5 可知，AA 模拟的结果高估了实际蒸散发，FAO-PM 模拟结果低估了实际蒸散量。由4 个性能模型评价指标可知（表3），FAO-PM 线性回归率最小为0.73，AA、PT、CRice接近于1（0.85～1.04）。AA、PT、CRice的相关性指标R2表现得较好，其值接近于0.90。纳什效率系数NSE中PT、CRice比AA、FAO-PM 表现得好，其值分别为0.86、0.90。AA 高估了实际蒸散发量（ME=-0.27 mm·d-1，RMSE=0.53 mm·d-1），FAO-PM 低估了实际蒸散发量（ME=0.44，RMSE=0.74 mm·d-1），CRice、PT 模拟结果与实测值较接近。由结果分析得出，年尺度蒸散发模型对高寒草甸适应性大小排序为：CRice＞PT＞AA＞FAO-PM。

表3 年尺度蒸发模型的性能Table 3 Performance of evaporation model at the annual scale

2.3 不同冻融阶段模型评价

年尺度的模拟效果要优于基于不同冻融阶段（表4）。4 个模型以年尺度为时间尺度的NSE 值均大于0.5，而不同的冻融阶段的NSE 值存在小于0.5。4 个模型与实测值的10 日滑动平均线比较如图6所示，4个模型的模拟结果与实测值变化趋势以及峰值出现时间点基本一致。

表4 不同冻融阶段蒸发模型性能Table 4 Performance of evaporation model in different freeze-thawing stages

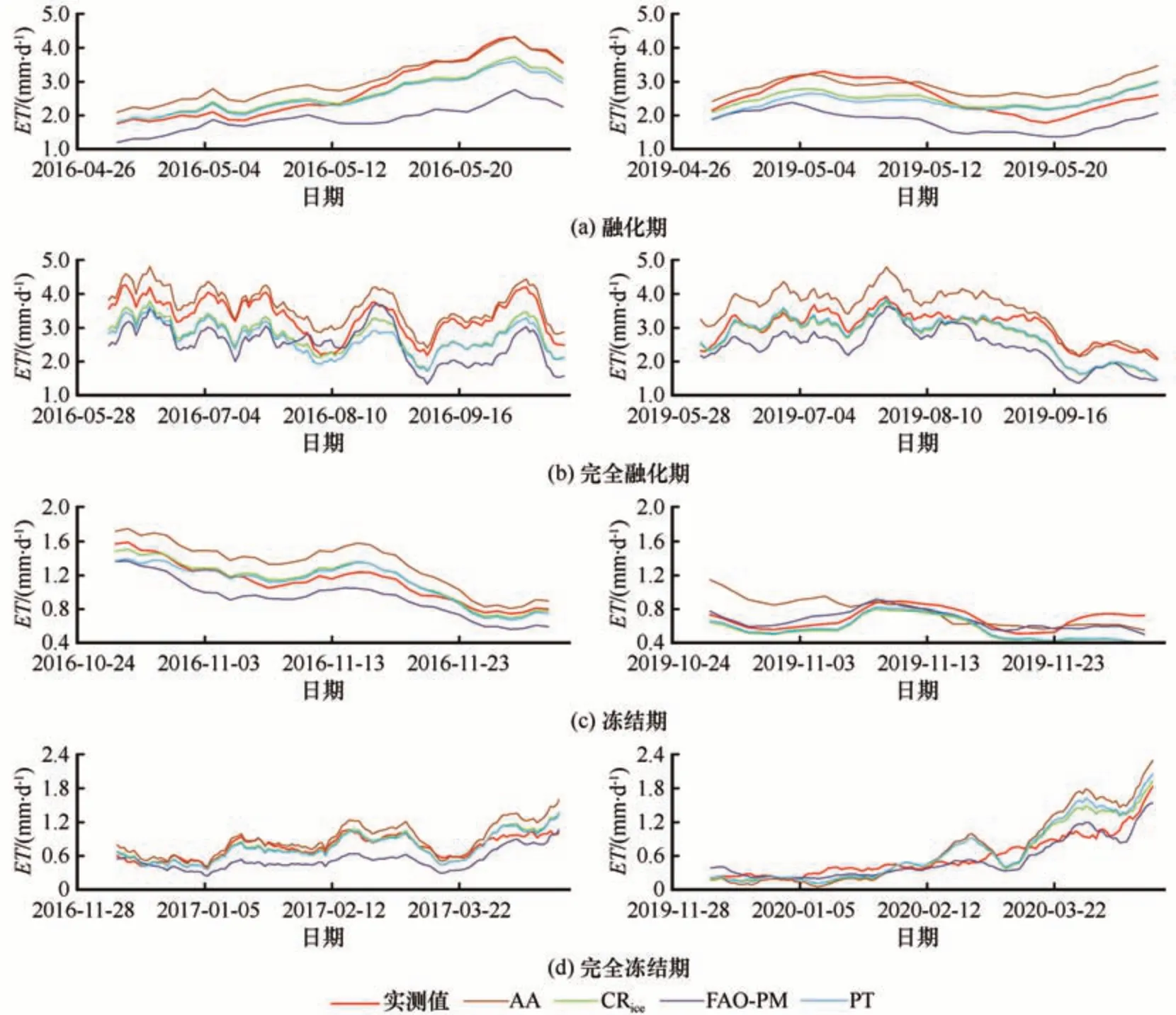
图6 2016年、2019年模型模拟值与观测值10日滑动平均线比较Fig. 6 Comparison of simulated evaporation and observated evaporation （10-day average） in 2016 and 2019

融化期CRice的平均值以及中位数与实测值差距较小，总体偏差优于其余3 个模型，模拟效果最优；PT、FAO-PM 不同程度低估了实际蒸散发，AA高估了实际蒸散发，其中FAO-PM 与实际蒸散发偏差最大（图7）。CRice与PT 在2016 年融化期模拟结果在前半段高估实际蒸散发在后半段低估实际蒸散发，2019 年与之相反。该时期模型模型性能排序：CRice＞PT＞AA＞FAO-PM。

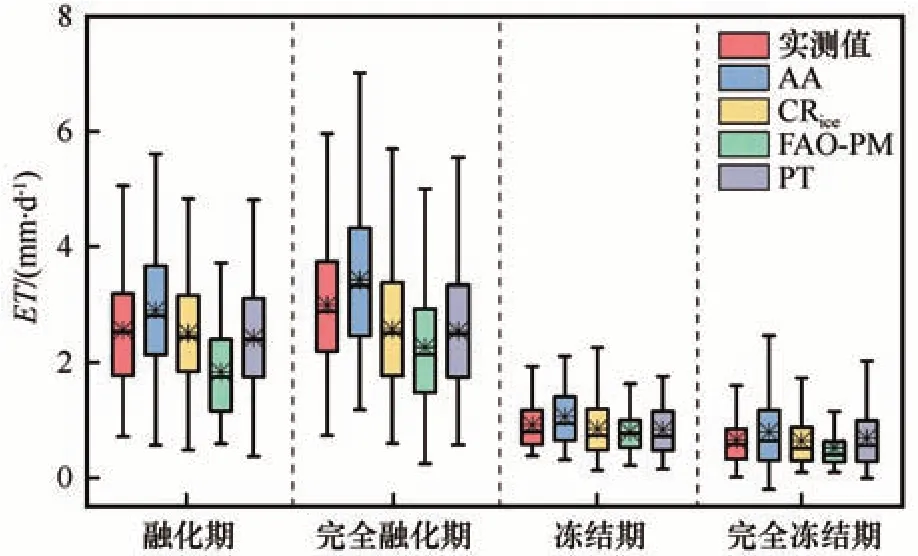
图7 模型模拟值与观测值对比的箱型图Fig. 7 Comparison of simulated evaporation and observated evaporation

完全融化期波动程度大，4 个模型与实测值变化趋势基本一致，CRice、PT 模拟结果与实际蒸散发误差较小，FAO-PM 明显低估实际蒸散发，AA 明显高估实际蒸散发；该阶段CRice模拟效果最优，FAOPM 总体偏差最大，AA 的中位数和均值均高于实测值，FAO-PM 均低于实测值。4 个模型性能排序：CRice＞AA＞PT＞FAO-PM。

冻结期4个模型的模拟结果与实测值均呈现下降趋势，AA 模拟结果高估了实际蒸散发，PT、AA、FAO-PM 均低估了实际蒸散发，该阶段CRice模拟效果最优。4 个模型整体偏差在不同的冻融阶段较小，4个模型性能排序：CRice＞PT＞FAO-PM＞AA。

完全冻结期波动程度小，4 个模型与实测值中位数均大于均值，AA、CRice、PT 均高估实际蒸散发，FAO-PM 低估实际蒸散发。2019 年12 月—2020 年4月4个模型与实测值存在峰值不同步现象，其可能原因是受完全冻结期间高寒恶劣环境影响，实际蒸散发存在观测误差。该阶段，CRice模拟效果最优，AA 模拟结果与实测值偏差较大；PT、FAO-PM 以及CRice与实测值总体偏差较小。4 个模型性能排序：CRice＞PT＞FAO-PM＞AA。

3 讨论

本研究表明基于非线性互补理论CRice最佳。原始CR 模型在严格的物理边界条件下修正干燥和湿润条件下互补理论模型计算蒸散发所产生的误差［14］，削减土壤冻融循环含水量变化对模型模拟性能的影响。原始CR、PT、AA 以及FAO-PM 模型都未考虑青藏高原冻融循环冰水相变中能量消耗的问题，冰从固态到气态经历了两种相变，融化和蒸发，这都需要消耗能量。在计算蒸散发的理想条件下，地下冰的广泛分布及其复杂的相变过程，需要考虑冰相变所消耗的能量，Wang等［20］在推导CRice模型时考虑了冻融循环中时期冰水相变所消耗的能量，使其模拟结果能够更加真实地反映实际蒸散发的变化趋势。随着温度升高，活动层深度的增加［5］，冰水相变可能将更加剧烈，未来青藏高原典型多年冻土蒸散发模拟研究中，考虑冰水相变所带来的影响，对进一步减少蒸散发模拟的不确定性具有重要作用。

尽管FAO-PM 模型对不同的下垫面以及气候条件的适应性较强，但在本文研究中发现FAO-PM在高寒草甸蒸散发模拟的应用中的与实测值存在较大偏差。在融化期、完全融化期，FAO-PM 模型模拟结果普遍低于实测值（ME 均大于0.6 mm·d-1）。姚天次等［26］在使用FAO-PM 模型对青藏高原蒸散发进行研究时，发现FAO-PM 模型所计算的蒸散发与日照时长成正相关，随着青藏高原实际蒸散发的增加，云量增多［6］，日照时长减少，而融化期和完全融化期的蒸散发量占全年的主导地位，云量处于最大阶段，因此导致FAO-PM 模型模拟结果偏小。此外，Cai 等［32］研究指出FAO-PM 应用于干旱区蒸散发模拟时，模拟结果普遍低于实测值，其原因是干旱区全年大部分时间最低气温Tmin＞露点温度Tdew，低估水汽压亏损（VPD），使得蒸散发模拟结果偏低。

AA 模型应用于高寒草甸蒸散发模拟时，结果表明融化期以及完全融化期模拟值偏大。融化期以及完全融化期时，降雨量增大，土壤及地表水分增加，此时高寒草甸所处的环境十分湿润。在湿润条件下AA 模型模拟的结果明显高估了实际蒸散发，这与Crago 和Brutsaert 的研究结果相似［22］。在完全冻结期，降雨量减少，环境较为干燥，此时AA模型模拟结果偏大，然而，研究表明在干燥环境下，AA 模型模拟结果偏小［13］，产生此现象的原因可能是风函数的选取以及粗糙度长度估计的不确定性［33］，此外，受完全冻结期高寒恶劣气候影响，实际蒸散发监测可能产生误差。

基于辐射法的PT 模型对高寒草甸蒸散发的模拟结果次佳。PT 模型不需要空气动力和表面阻力作为输入参数，只需要常规的气象数据就能驱动，粗糙长度估计的不确定性对蒸散发模拟没有影响，同时作为PT 模型的主驱动参数净辐射和温度具有较低的观测不确定性［33］，这使得PT模型模拟结果相对良好。但是PT模型忽略了陆面植被，土壤类型等对蒸散发的作用［34］。植被性质，土壤性质，会影响径流系数，径流系数反过来又会影响蒸散发，这会对模型的模拟性能产生一定的影响［35］。

本文对于不同方法的蒸散发模型模拟青藏高原典型多年冻土区高寒草甸实际蒸散发的效果进行了评价，结果可为该地区高寒草甸蒸散发模拟应用研究提供一定的参考。然而受限于监测地区的数量，文中仅对典型多年冻土区某一处高寒草甸进行蒸散发模拟研究，缺乏对不同植被类型的研究，但青藏高原典型多年冻土区植被主要为高寒草甸以及高寒沼泽草甸，且本文研究区域风火山具有高寒草甸、多年冻土等下垫面特征的良好代表性，因此可以认为文本研究结果在多年冻土区高寒草甸植被条件下具有较好的适用性。

4 结论

本文以青藏高原典型多年冻土区风火山小流域为研究区，使用2015 年涡度观测数据对αPT进行标定，基于研究区2016—2017 以及2019—2020 涡度观测数据，评价了AA、PT、FA0-PM、CRice共4 种不同蒸散发模型在高寒草甸地区，全年以及不同冻融阶段蒸散发模拟过程中的模拟性能，主要结论如下：

（1）CRice模型模拟精度最高，PT 模型次之，AA、FAO-PM 模型模拟精度较差，RMSE 值分别为0.45 mm·d-1、0.49 mm·d-1、0.53 mm·d-1、0.74 mm·d-1；NSE 值分别为0.90、0.86、0.84、0.69。AA 模型模拟的蒸散发高于实测值，FAO-PM、PT 以及CRice低于实测值。

（2）在融化、完全融化、冻结以及完全冻结四个冻融阶段，CRice模型模拟结果在4 个蒸散发模型中与实测值误差较小，并且能够反映实际蒸散发的变化趋势，表明模型能够较好地体现冻融过程土壤冰水相变对高寒草甸蒸散发的影响

（3）尽管本文仅采用风火山一个站点的数据对比分析了不同模型，但由于该台站具有多年冻土、高寒草甸等下垫面特征的良好代表性，可以认为青藏高原以高寒草地植被覆盖的多年冻土区均具有适用性。