基于集合卡尔曼-Elman 网络的软测量建模方法

方港 袁珑华 王晓明 李艳 黄道平 于广平 叶洪涛 刘乙奇，5†

（1.华南理工大学 自动化科学与工程学院/自主系统与网络控制教育部重点实验室，广东 广州 510640；2.华南理工大学未来技术学院，广东 广州 511442；3.广州工业智能研究院，广东 广州 511458；4.广西科技大学 广西汽车零部件与整车技术重点实验室，广西 柳州 545036；5.华南理工大学 广东省无人机系统工程技术研究中心，广东 广州 510640）

软测量技术能够对工业过程中重要且难以在线测量的变量进行测量，并实现对过程变量的实时监控。近年来，随着人工智能技术的发展，基于数据驱动的软测量技术被广泛应用于工业过程中，成为了先进过程控制技术的重要组成部分，也是化工领域中用于难测过程变量检测的常用技术［1-2］。基于数据驱动的软测量建模技术无需获取精确的机理模型，其通过对数据的深度分析构建易测变量和难测变量之间的数学模型，利用易测的辅助变量估计难测变量［3］。基于神经网络的软测量建模方法凭借其强大的非线性映射能力、网络拓扑结构和鲁棒性，以及不依赖于数学模型的特性，成为了软测量领域最为活跃的研究分支［4-6］。但是，强非线性、参数时变、多变量耦合使得利用传统前馈神经网络建立的模型存在检测不清、故障诊断不明和实时控制不准等问题。递归神经网络（Recurrent Neural Network，RNN）的处理单元间既有内部的反馈连接又有前馈连接，具有动态记忆特性，能够处理具有时延信息的数据，从而具有比前馈神经网络更强的动态行为和计算能力［7］。作为最典型的RNN 之一，Elman 递归神经网络在水质软测量模型中得到了较好的应用［8］。关学忠等［9］对污水处理厂曝气池中的化学需氧量（Chemical Oxygen Demand，COD）进行学习预测，证明了Elman网络对污水COD的预测能力优于反向传播（Back Propagation，BP）神经网络。

然而，现有Elman 神经网络的训练算法多采用时间反向传播（Back Propagation Through Time，BPTT）［10］、动量梯度下降（Gradient Descent with Momentum，GDM）和Levenberg-Marquardt（LM）［11］等传统优化算法［12］。这些基于梯度下降的算法存在对初始值设置敏感、计算结果不稳定、易收敛到局部最优解和梯度消失等问题［13-14］，而卡尔曼滤波算法（Kalman Filter，KF）［15］的提出为上述问题提供了一个解决思路［16］。Hao 等［17］采用基于扩展卡尔曼滤波器（Extended Kalman Filter，EKF）的神经网络训练方法，提高了传统神经网络的迭代收敛速度和精度，但每次迭代计算量大。EKF方法采用一阶泰勒近似，需要计算雅克比矩阵，在局部非线性较强时容易引入较大的近似误差，导致滤波器失效，不利于并行计算［18-19］。为此，研究者们尝试引入集合卡尔曼滤波（Ensemble Kalman Filter，EnKF）以避免上述问题［20-21］。

EnKF 是 由Evensen［22］提出的一种数据同化方法，适用于高维、非线性和非高斯状态估计问题［21］，目前在神经网络的参数优化领域得到了广泛应用。Legler 等［23］将EnKF 与标准人工神经网络（Artificial Neural Network，ANN）相结合来优化浅水模型参数，减小了大气变量的状态误差，有效量化了参数估计的不确定性，但其预测能力在实际数据的表现仍有待进一步研究。Mirikitani 等［24］通过将EnKF 与递归神经网络有序结合，验证了EnKF 在RNN 的时间序列预测上具有很好的适用性。此外，Chen等［25］采用EnKF 训练长短期记忆网络，将其作为捕获预测不确定性的无梯度替代方案。

为避免雅克比矩阵的计算，并规避标准算法不适用于大型神经网络的难题，文中将EnKF 引入Elman 递归神经网络中更新网络参数，以期获得一种简单、无梯度的神经网络训练方法，提高软测量模型的预测性能。

1 Elman 递归神经网络及其状态空间模型

1.1 Elman递归神经网络的基本架构

神经网络是目前最常使用的软测量模型，文中采用Elman 递归神经网络进行动态非线性建模。Elman 网络也称为简单递归神经网络（Simple Recurrent Network，SRN），是一种典型的局部回归网络［26］。与前馈网络相比，Elman 网络引入了一个特别的隐含层，称为关联层。关联层保存了上一时刻的隐含层状态信息，并与当前时刻的网络输入一起作用于隐含层，这相当于引入了状态反馈。这种内部反馈增加了网络动态特性，可实现动态建模。

Elman 网络一般分为4 层：输入层U，隐含层R，承接层C 和输出层Y。用WRU、WRC、WYR分别表示输入层到隐含层、承接层到隐含层、隐含层到输出层的连接权值矩阵。隐含层输出经单位时延后作为下一时刻承接层的输入，即ck=vk-1，并经权值矩阵WRC作用到隐含层。

给定k时刻的输入uk∈Rn，Elman 网络的输出可以计算为

式中，fh(·)为隐含层激活函数，fo(·)为输出层激活函数，n、Nh、m分别表示输入层、隐含层、输出层的结点个数。文中隐含层激活函数采用sigmoid函数fh(x)=，输出层采用线性激活函数fo(x)=x。

Elman 神经网络引入的内部反馈增加了网络动态特性，便于动态建模，但同时也使模型结构变得复杂，训练时更易陷入局部最小值。训练Elman神经网络的方法较多，比较常用的有BPTT 算法、GMD和LM算法等［10-12］。

1.2 动态状态空间建模

递归神经网络、前馈神经网络、径向基函数（Radial Basis Function，RBF）神经网络等的学习问题本质上是参数优化问题，通过对模型参数（权值）的不断调整，使性能函数（如均方根误差）的值不断减小。

将集合卡尔曼滤波技术引入神经网络中，本质上是把神经网络中各神经元之间的连接权值参数作为随机变量，即滤波器的状态，采用动态状态空间框架，随着时序k不断优化网络的参数，使得网络的目标输出与预测输出之间的均方误差逐渐减小，进而提高网络的训练精度。利用卡尔曼框架编写神经网络的状态空间模型如下：

式中：xk为由权值参数所组成的状态向量；uk为输入向量；zk为模型输出；rk为过程噪声向量，假设rk～N(0，Rk)；vk为测量噪声向量，假设vk～N(0，Vk)；g（·）为神经网络函数，文中g（·）为Elman递归神经网络，也可以将其扩展到前馈神经网络（Feed Forward Neural Network，FFNN）、RBF等网络中。

2 基于集合卡尔曼滤波的Elman 网络算法

2.1 基于基本集合卡尔曼滤波的Elman 网络算法

EnKF是一种基于随机采样的卡尔曼滤波方法，它通过随机采样产生的粒子集来拟合状态分布，用粒子集的协方差信息代替系统协方差，简化了卡尔曼框架中协方差矩阵的分析过程。当新的数据到来时，EnKF 对粒子集中的每个粒子进行更新，从而不断调整概率分布，因此，EnKF更便于实现。

应用基本EnKF 算法可以对Elman 网络参数进行估计。对于式（4）的状态空间模型，基于EnKF滤波的Elman网络参数学习过程（EnKF-Elman）可整理为以下步骤。

步骤1由初始状态的均值和协方差随机采样生成由集成粒子xk，i∈Rn（n为状态维度）组成的粒子集：

式中，N为集成粒子个数，Xk为k时刻的粒子集合。状态分布的均值和协方差可以由这N个集成粒子来近似：

式中：1N∈RN，是维度为N、元素均为1 的列向量；表示去均值后的粒子集合，

步骤2计算Elman模型的预测粒子集：

分别用和Yk表示粒子转移状态和粒子输出的组成矩阵：

步骤3粒子更新——给定测量值zk∈Rm，其粒子集的更新方式如下：

式中：Hk为输出zk相对于网络权重xk的雅可比矩阵；εk为施加在每个粒子上的扰动观测向量所组成的扰动矩阵，它可以有效避免协方差矩阵的过度低估［27］；为粒子集的协方差，可由其去均值后的矩阵进行计算，具体计算方法可参照式（7）和（8），那么可将粒子集的更新方式写为

式（14）的更新需要计算Hk，更简便地，可以采用直接计算Hk的方法［28］：

在实际应用中，为加快运算速度并避免矩阵求逆的问题，往往采用奇异值分解（Singular Value Decomposition，SVD）的方法进行计算［27-28］，即

这样，算法的编程实现可以更加高效、快速。

EnKF根据测量数据循环迭代步骤2和3，不断调整粒子集分布，从而实现Elman 网络的参数更新。可以发现，EnKF 只需要更新粒子集，因此有效解决了KF 框架在计算和更新状态误差协方差时对计算资源需求量过大的问题；同时，其不需要求解和计算雅克比矩阵，易于实现，便于扩展。

2.2 基于对偶有限样本集合卡尔曼滤波的Elman网络算法

相比EnKF-Elman，基于对偶有限样本集合卡尔曼滤波（Dual Finite-Size Ensemble Kalman Filter，D-EnKF-N）的Elman 网络算法主要在于滤波器的不同，其采用的是D-EnKF-N 滤波器。在介绍D-EnKF-N 滤波器前，先介绍有限样本的集合卡尔曼滤波（Finite-Size Ensemble Kalman Filter，EnKF-N）方法。

2.2.1 有限样本的集合卡尔曼滤波方法

EnKF-N 本质上不需要像基本集合卡尔曼滤波一样引入扰动观测矩阵，其主要思想是：式（6）和（7）计算得到的集合均值和协方差与先验概率密度函数（Probability Density Function，PDF）的均值Xb和误差协方差B不匹配；对于较大的样本（N→∞），它们是接近一致的，但由于采样误差的存在，对于较小的样本它们往往是不一致的。为此，EnKF-N 在EnKF 中提出了一种新的先验PDF，它是对所有可能的Xb和B进行积分的结果：

式中：det|·|表示矩阵的行列式；εN是一个取决于先验分布假设的常数，如果集合均值Xˉ与Xb一致，则εN=1，否则。由于预测先验公式（18）是非高斯的，需要通过类似于变分优化的最大似然滤波器进行分析［29］。在集合空间中，状态被向量∈RN参数化，使得

此时，EnKF-N的代价函数为

那么，式（19）中的可通过最小化式（20）得出：

式中：VT为满足VT1N=1N的任意正交矩阵；为集合空间中的分析误差协方差矩阵，其计算方式为

2.2.2 基于D-EnKF-N的Elman网络算法原理

因为D(ς)是一个标量函数，式（25）的全局最小值很容易找到。变量ς与平方半径共轭，其可以看作是粒子集中有效自由度的数量。D(ς)的最小值ςa可以通过在区间[0，N/εN]上最小化以下对偶代价函数来实现［31］：

一旦计算出最小值ςa，就可以从类似式（21）的代价函数中获得对w的分析：此时，通过式（22）和（24）可对粒子集进行更新，详细信息可以参阅文献［31-32］。D-EnKF-N 与Elman网络相结合构建软测量模型的步骤总结如下。

对比EnKF-Elman和D-EnKF-N-Elman算法，可以发现它们本质上是为了缓解粒子集的分布与状态参数的实际分布不匹配问题而采取了不同的措施。EnKF-Elman 算法在训练过程中通过引入扰动观测矩阵来缓解协方差矩阵的过度低估问题，其训练过程简单，易于实现，但在迭代过程中引入了随机性，可能产生次优的滤波性能；D-EnKF-N-Elman算法采用新的先验概率密度函数进行分析，避免了每次迭代过程中扰动观测矩阵的随机性影响，性能更好，但是增加了算法的复杂度。

3 实验分析

3.1 案例说明

为了验证所提出的算法的优越性，文中使用加州大学欧文分校机器学习数据库中的污水数据（UCI数据）进行仿真。UCI 数据来源于一间城市活性污泥污水处理厂，由于该厂的污水处理工艺较为落后，5 日生物需氧量BOD5在线分析仪往往不可靠。此外，实验室测量过程又存在固有的5天延迟，难以实时获取BOD5值，给污水的有效处理带来了挑战，因此非常需要一个合理、准确的预测模型来对BOD5等重要的出水指标进行预测。

如图1 所示，该厂的污水处理过程由4 部分组成［33］：预处理、初沉池、反应池和二沉池。该厂每天对38 个与有机物和微生物相关的过程变量进行测量。受测量条件的限制，设备故障、传感器失灵、天气、人为等因素均会对变量的测量产生影响，导致仅有275天的正常数据。对此，文中首先结合机理分析对变量进行了初步筛选，最终选择18个过程变量作为模型的输入［34-35］，详细的变量介绍见表1。

表1 UCI辅助变量Table 1 UCI auxiliary variables

图1 污水处理过程Fig.1 Sewage treatment process

研究中选择工厂出水中的化学需氧量（CODS）、生物需氧量（BOD5）和固体悬浮物浓度（ρSS，S）作为输出变量。

为评价模型的预测精度，分别引入均方根误差（Root Mean Square Error，ERMSE）、平均绝对百分比误差（Mean Absolute Percentage Error，EMAPE）和相关系数R作为性能指标，它们的数学表达式分别为

式中：N为样本个数；和yi分别为第i个样本的预测值和输出值；cov(Y，Y)为协方差；var(Y)和var()分别为Y和的方差；=(，，…，)，Y=(y1，y2，…，yn)。ERMSE衡量的是真实值与预测值偏离的绝对大小，而EMAPE衡量的是预测值偏离真实值的相对大小（即百分率），R主要用来衡量模型对数据变化趋势的拟合程度。显然，ERMSE和EMAPE越小，模型的预测误差和偏离实际值的程度越小，效果越好；R越大，模型越能很好地跟踪数据的变化趋势，性能也就越好。

考虑到文中使用Elman网络作为多输出模型同时预测多个响应，因此用对角平方和的均方根ERMSSD和多元相关系数RMR作为多输出的性能评价标准。这些评价标准的计算公式如下：

式中，trace{·}表示矩阵的迹，Ri为第i个输出所对应的相关系数。对于软测量模型而言，ERMSSD越小、RMR越大，则预测性能越好。

性能评估时，采用ERMSE、EMAPE和R这3 个指标来评价各输出变量的预测精度和偏差率，采用ERMSSD和RMR来评价多输出模型的整体预测性能。

3.2 实验结果

为了验证集成卡尔曼滤波技术在Elman网络软测量模型上的有效性，将其用于预测UCI数据集的ρSS，S、BOD5和CODS，并将其和使用经典训练算法的Elman 网络（BPTT-Elman、GDM-Elman、LM-Elman）进行对比，评估其预测性能。为了方便书写，下文用EnKF-Elman 表示集合卡尔曼滤波的Elman 软测量模型，用D-EnKF-N-Elman 表示基于对偶有限样本的集合卡尔曼滤波的Elman软测量模型。

为便于对比，实验中所采用的网络结构均为18-8-3 的Elman 网络结构，而隐含层激活函数和输出层激活函数分别使用sigmoid 函数fh(x)=和线性激活函数fo(x)=x；权重的初始值介于［-0.5，0.5］；将UCI 的400 组数据中的前200 组样本用于训练模型，后200组用于验证模型性能。考虑到受初始权重随机性的影响，表2中结果是使用300次随机的初始权值运行得到的平均结果。

表2 不同集成粒子个数下EnKF-Elman模型的预测结果1）Table 2 Prediction results of EnKF-Elman model with different particle numbers

表2 给出了不同算法的预测结果。可以看出，当集成粒子个数M为500时，基于集合卡尔曼技术的Elman软测量模型已能得到较好的预测效果，性能显著优于BPTT-Elman、GDM-Elman 和LM-Elman等传统Elman网络。

以EnKF-Elman 为例，从单个输出的预测指标ERMSE、R和EMAPE来看，集合卡尔曼滤波方法的粒子个数为500 时，EnKF-Elman 在ρSS，S、BOD5和CODS上的ERMSE分别为3.379、1.897 和8.667，比BPTTElman分别减小了31.83%、47.17%和46.25%，比GDM-Elman分别减小了26.51%、42.65%和40.14%，比LM-Elman分别减小了86.98%、43.51%和35.95%，这表明文中提出的EnKF-Elman 方法在水质参数预测上比传统Elman 模型的测量误差更小，性能更优。

EnKF-Elman 在各个水质质量参数输出的EMAPE和R上同样有类似的提升，具有较好的性能表现。从整体预测性能ERMSSD和RMR来看，EnKF-Elman 的ERMSSD减少到了9.499，RMR达到了0.911，比BPTTElman 分别提升了45.00% 和32.41%，比GDMElman 分别提升了38.99% 和16.65%，比LMElman 分别提升了69.71%和19.08%，这说明集合卡尔曼滤波方法提升了Elman网络的预测性能，可对系统多水质参数进行有效检测。

对比EnKF-Elman 和D-EnKF-N-Elman 可以发现，对偶形式的有限样本集合卡尔曼滤波比标准形式的集合卡尔曼滤波的预测结果略优，能够更有效地提高Elman网络的预测性能。

图2 和图3 为不同算法的输出预测曲线。为了方便观察，仅列出前100 个测试数据的预测结果。对比基于BPTT、GDM 和LM 的传统算法的预测结果，可以看出文中基于EnKF 的算法能够更好地跟踪输出变量ρSS，S的动态变化。传统算法中的输出水质参数ρSS，S的预测值与实际值的拟合较差，这主要是因为算法容易陷入局部极小值，得到较为不理想的预测结果，这反过来证明了文中方法的有效性。对于变量BOD5和CODS，BPTT-Elman、GDM-Elman和LM-Elman 等传统算法具有良好的拟合性能。但从预测曲线的峰值和峰谷来看，基于EnKF 技术的Elman 网络能够更好地跟踪实际曲线的动态变化，其预测能力优于上面列出的传统Elman 训练算法，这说明EnKF-Elman 可以很好地拟合预测水质参数的变化趋势。

图2 BPTT-Elman、GDM-Elman 和LM-Elman 模型的输出预测曲线Fig.2 Output prediction curves of BPTT-Elman，GDM-Elman and LM-Elman models

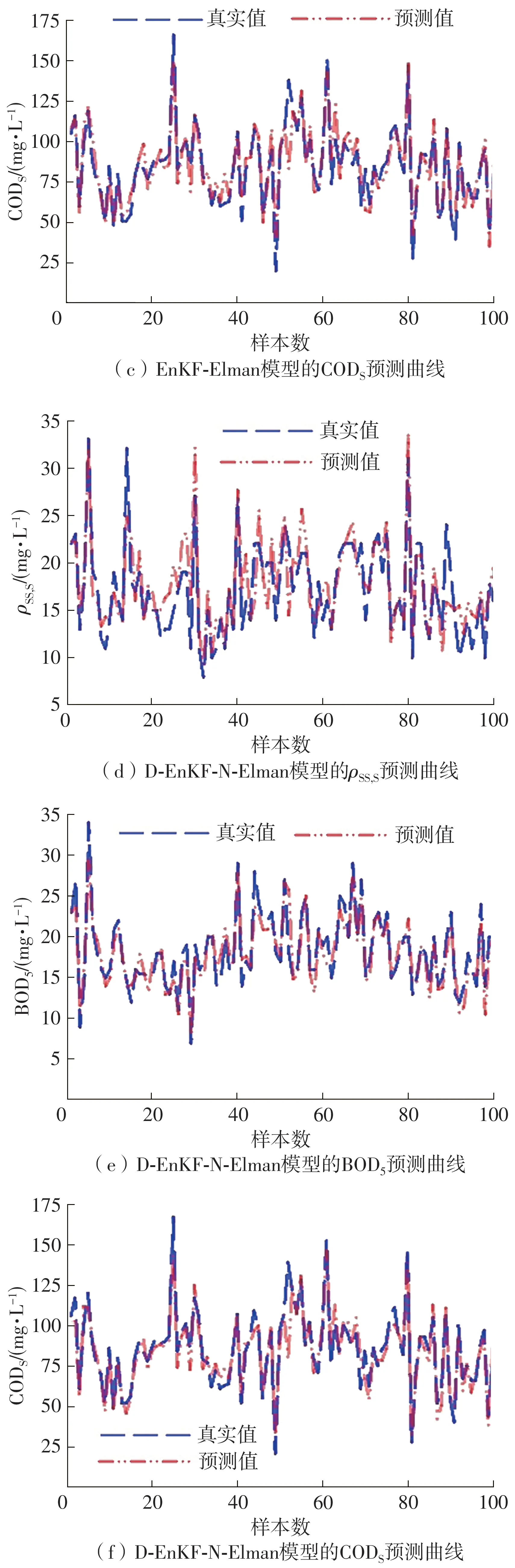
图3 EnKF-Elman 和D-EnKF-N-Elman 模型的输出预测曲线（M=500）Fig.3 Output prediction curves of EnKF-Elman and D-EnKFN-Elman models（M=500）

图4 为基于集合卡尔曼技术的Elman 网络的收敛曲线。可以看出，D-EnKF-N-Elman 的收敛精度比EnKF-Elman的略高，说明D-EnKF-N-Elman的收敛性能更好。这主要是因为D-EnKF-N 滤波器在先验中考虑了采样误差，而且不需要像集合卡尔曼滤波器一样引入扰动观测矩阵，可以有效减小采样误差。但是，EnKF-N 类方法计算更加复杂，其训练时间要求更高。

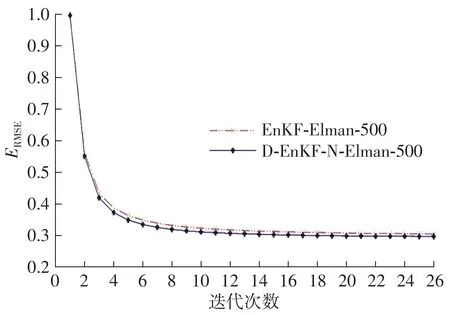
图4 EnKF-Elman 和D-EnKF-N-Elman 模型的平均ERMSE 收敛曲线Fig.4 Average ERMSE convergence curves of EnKF-Elman and D-EnKF-N-Elman models

4 结语

文中针对传统Elman 神经网络预测精度欠佳、容易陷入局部最小值的问题，将集合卡尔曼滤波技术引入到Elman 网络中构建软测量模型，采用UCI数据进行验证，对ρSS，S、BOD5和CODS等重要污水出水水质参数进行预测，并将结果与传统的模型进行对比，发现EnKF-Elman和D-EnKF-N-Elman模型无论是单输出还是多输出评价指标，其预测性能都优于传统的Elman模型，说明文中提出的方法是有效和可行的。但随着系统复杂度增加，EnKF 算法占用的内存会大幅增加，后续研究中拟引入解耦方法，以提高算法的运行效率和实用性。