系泊形式对浮式风力机动力响应的影响

张若瑜 李耀隆 李焱 李昊然 黎国彦 唐友刚

（天津大学 天津市港口与海洋工程重点实验室/水利工程仿真与安全国家重点实验室/建筑工程学院，天津 300350）

近年来，风能以其储量大、干净、可持续等诸多优点，逐渐成为未来最有发展前景的能源之一。当前，海上风电有着发电量高、单机装机容量大、机组运行稳定、大规模开发适合性强等优点，成为全球电场建设的热点。我国拥有18 万公里长的海岸线，海洋资源丰富，海上风电的开发潜力巨大。近年来，我国海上浮式风力机装机量在不断提升，据统计，“十四五”期间，全国海上风电规划总装机量将超100 GW。在海洋强国建设的深海战略以及国家绿色发展的双碳战略双重背景下，海上风电开发正成为能源研究与发展的重点方向［1］。

海上风力机基础型式主要分为固定式与漂浮式两种，主要区别在于其与海底的连接形式。固定式风力机通常通过插入海底的桩腿或者导管架来保证结构的稳定性。固定式风力机一般于水深小于50 m的近岸浅水区域使用，因此在选址上受到多种外部因素的制约。另一方面，离海岸线更远的区域风速更大并且更稳定，更适合于风力发电，漂浮式风力机由此应运发展起来［2］。

海上漂浮式风力机系统主要由风力机、浮式基础、系泊系统3部分组成。其中浮式基础大多基于海上油气平台的设计理念，主流型式有半潜型基础（SEMI）、单柱型基础（SPAR）、张力腿型基础（TLP）等［3］。具有良好运动性能的浮式基础才能保证风机的正常作业。面对复杂多变的海洋环境，设计一种具有优良动力响应特性的浮式基础是海上浮式风力机建造开发的核心问题之一。根据有关统计，目前全世界的浮式基础细分约有30 种。对于不同型式的基础需要采用与之相匹配的系泊系统，以保障浮式风力机可以在目标海区内稳定作业。因此，系泊系统作为整个浮式风力机系统安全与高效作业的关键一环，其对于风力机的动力响应有至关重要的影响。

通常，半潜型与单柱型基础采用悬链线式系泊系统，而张力腿型基础由于储备浮力大而采用张紧的筋腱进行定位系泊。国内外学者针对采用漂浮式风力机的系泊系统动力响应开展了相关的研究。Bae等［4］开发了一种气动-水动-伺服-弹性-系泊耦合的时域动力分析模型，研究了系泊缆瞬态断裂情况半潜型风力机的动力响应；Brommundt等［5］提出了一种优化浮式风力机系泊系统的方法；李焱等［6］考虑系泊系统的非线性系泊力情况，研究SPAR 型浮式风力机系统的动力响应，对浮式风力机在作业海况和极限海况下的动力响应进行分析；樊天慧等［7］考虑深水悬链线静力特性，基于遗传算法开发悬链线锚泊系统的截面优化设计程序。针对张力腿式系泊系统，冯丽梅等［8］对张力腿平台系泊系统分段建立分析模型，提出在时域内计算张力腿筋腱张力响应RAO 的方法；吴浩宇等［9］在时域中研究了张力腿浮式风力机筋腱失效模式下的瞬态响应；程阳［10］基于南海海洋环境，设计了适用于200 m 水深的张力腿浮式风力机，并研究其张力腿筋腱疲劳问题，结果表明二阶波浪力使张力腿筋腱应力幅值显著增加。

近年来，针对我国过渡水深海域，提出了一种浅吃水型漂浮式基础，并针对其动力响应特性开展了相关研究。结果表明，通过增大底部减动结构直径可有效减小纵摇运动和系泊缆张力，同时对系统断缆后的动力响应进行了评估，分析其在极端海况下的风险［11-12］。这些工作均是采用悬链线系泊系统开展的，本文采用这种新型基础的5 MW 漂浮式风力机为研究对象，分别提出悬链线式与张力腿式两种系泊方案，并建立风力机-基础-系泊系统耦合动力学数值模型，对其作业状态下的动力响应特性进行对比研究，分析不同系泊方式下该型浮式风力机的动力响应特点。

1 浮式风力机

1.1 浮式基础与风力机

为上部风机提供支持力的浮式基础是整个浮式风力机系统的关键结构，本文参考一种基于OC3-Hywind SPAR 型浮式风力机的结构型式，提出具有减动结构的浅吃水SPAR 型浮式基础［11-12］，其主要原理是令结构重心低于浮心以获得稳定平衡。因此，为保证足够的浮力，设计的结构尺寸及其主视图与俯视图见图1，主要参数如表1所示。

表1 新型浅吃水浮式基础基本参数Table 1 Main parameters of the new-type reduced-draft SPAR type floating foundation

图1 新型浮式基础（单位：m）Fig.1 New-type floating foundation（Unit：m）

整个浮式基础主要包含4个部分：顶部是用于和塔架相连接的圆台；中部采用圆锥式结构进行过渡，增强浪溅区的结构强度，并有效防止应力集中；水线面以下采用细长圆柱体结构，以减小浮体在波浪卓越区的水动力载荷；底部整个结构通过加装底部环形减动结构，为浮式风力机提供足够的浮力的同时，有效降低结构重心，从而提高运动稳定性。

上部风力机采用的是具有公开翼型数据的、美国可再生能源实验室（NREL）开发的5 MW海上风力机［13］，其主要参数具体见表2。

表2 NREL 5 MW风力机的主要参数Table 2 Parameters of NREL 5 MW baseline wind turbine

1.2 系泊系统

悬链线式系泊系统通常由多根锚链或钢缆构成，在水平面内呈辐射状，通过自身几何结构与重力对浮式基础进行系泊，结构形式相对简单且易于安装。张力腿式系泊系统则由多组垂直设置的张力筋腱组成，基础自重与浮力间的差值为张力腿提供预张力，使其处于刚性状态，从而实现对浮式基础在水平和垂向上良好的定位能力，但其施工复杂，安装成本较高。

笔者所在课题组的以往研究［11］证明了悬链线式系泊系统对该漂浮式基础的适用性，其中3根系泊缆均由无档锚链组成，如图2（a）所示。从表1的数据可以看到，新型浮式基础排水量有较大的裕度，恰好满足适用张力腿式系泊系统的基本要求。因此，本文参考现有张力腿式浮式风力机设计方案采用的张力筋腱设计参数［10］，提出了由3根垂向张力筋腱组成的张力腿式系泊系统，布置方式如图2（b）所示。悬链式系泊锚链以及张力筋腱的参数如表3所示。

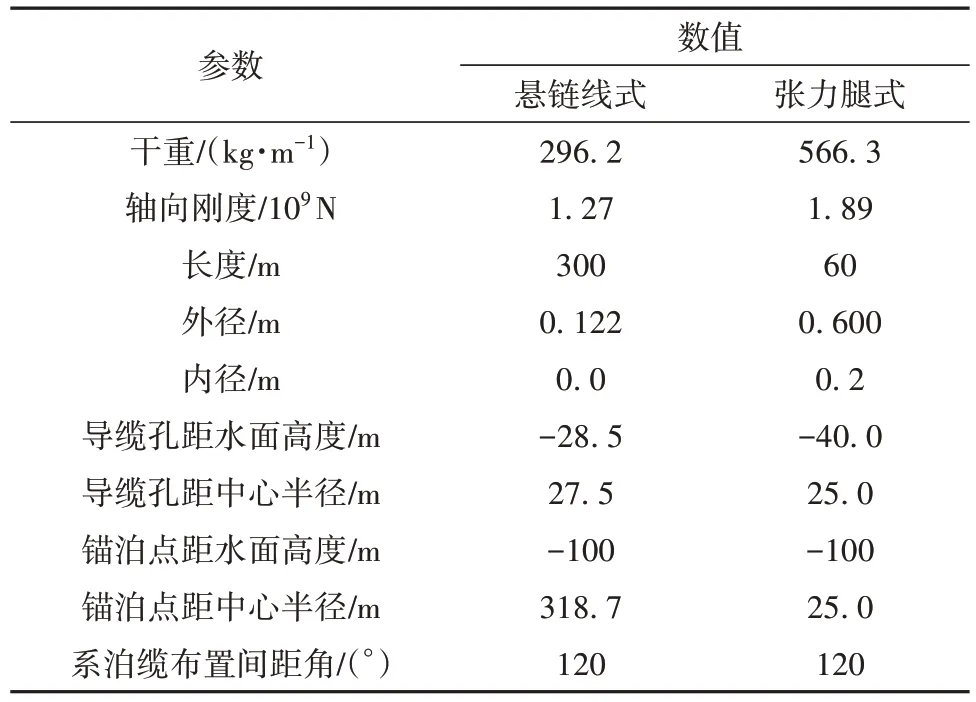
表3 系泊系统主要参数Table 3 Main parameters of the mooring system

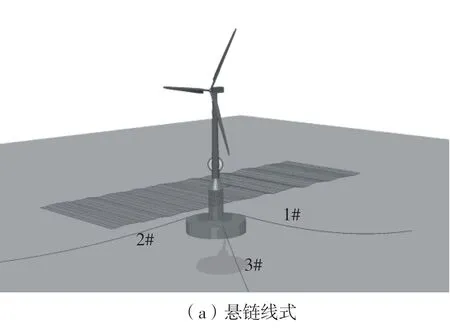
图2 浮式海上风力机Fig.2 Floating offshore wind turbine

2 数值计算

2.1 波浪载荷

本文采用三维势流理论计算带有大尺度减动结构的新型浮式基础受到的波浪载荷。在流域内，各质点的速度势Φ需要满足Laplace方程，即

入射波在传播过程中遇到结构物时，其速度势可划分为3个部分，分别是受扰动前的入射波速度势Ф1、因入射波接触结构物而发生绕射产生的绕射波速度势ФD、结构物在入射波作用下发生运动后带动周围流体产生的辐射波速度势ФR。速度势满足如下边界条件。

自由表面条件：

海底条件：

物面条件：

无穷远辐射条件：

式中，g为重力加速度，ω为波浪频率，n为物面外法向单位向量，Un为浮体法向速度，k为波数，R=

通过求解具有边界条件的Laplace 方程可得到速度势函数表达式，同时结合Bernoulli方程得到结构湿表面上每个速度势分量的压强分布，最后通过积分计算即可得到作用结构上的波浪力。

2.2 空气动力载荷

浮式风力机可以将捕获的风能转化为风轮的机械能，因此不能采用传统海洋结构物所受的风压载荷模拟。本文采用的叶素-动量理论［14］综合了叶素理论和动量理论两个理论的优势，叶素处相对风速是由风轮平面处的轴向速度（1-a）v0和切向速度（1+a′）wr合成的，其中a为轴向诱导因子，a′为周向诱导因子，v0为入射风速，w为风轮转速，r为叶素距轮毂的距离。利用动量定理，通过风轮的动量损失推导出轴向和切向的诱导速度，得到叶轮在各叶素位置处的轴向诱导因子和周向诱导因子，并将其作为中间参数，建立诱导因子与叶素气动载荷之间的关系式，通过迭代计算确定空气动力载荷。

式中，dT为局部推力，dM为局部转矩，ρ为空气密度。

2.3 系泊载荷

假定两个坐标系，用于描述柔性结构物载荷：全局坐标系OXYZ与局部坐标系O'VxVyVz如图3所示。

图3 全局坐标系与局部坐标系Fig.3 Global and local coordinate system

对于主要受到轴向拉力的系泊缆可以采用变形杆单元模拟计算其内力，如图4 所示。基于Bergan方法，空间杆单元可以采用总体拉格朗日公式表达，并基于综合横截面力和小应变理论进行修正。根据小应变理论，假定为初始无应力单元长度。因此，单元的轴向力N由式（7）给出，即

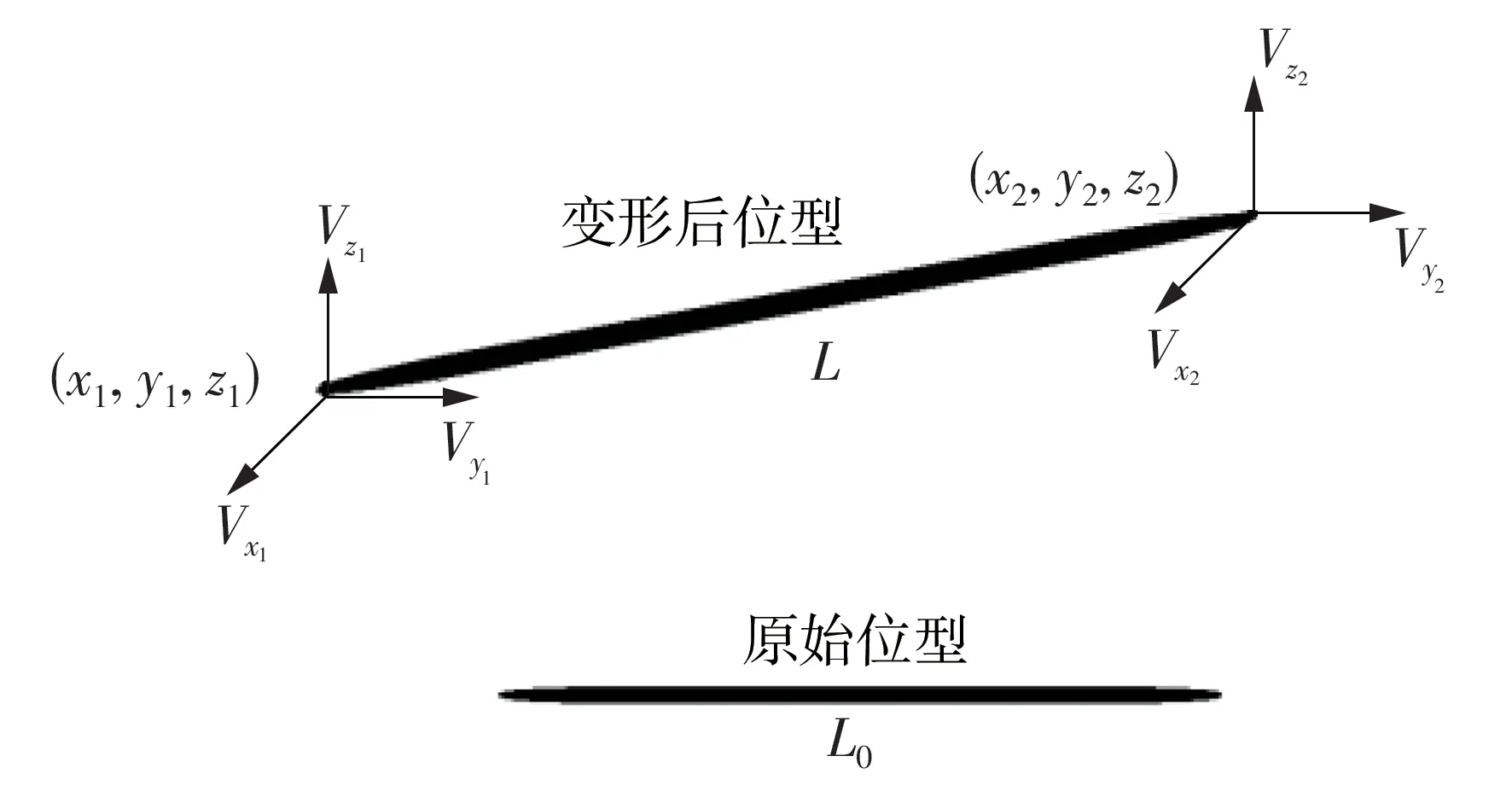
图4 杆单元Fig.4 Bar element

式中，L0为初始无应力单元长度，L为变形后单位长度，E为弹性模量，A为横截面积。通过虚功原理的增量形式得到单元的切向刚度关系：

式中，ΔSint为内力向量增量，kG和kM分别为几何刚度矩阵和材料刚度矩阵，Δv为位移增量向量。

2.4 柔性体有限元模型

将叶片等柔性体简化为悬臂梁模型，并采用有限元方法离散。每个有限元单元的质量me与弹性刚度矩阵ket为

式中：ρe为单位密度；l为单位长度；N为单位形函数矩阵；I为截面惯性矩。

2.5 时域运动方程

本文的浮式风力机基础运动控制方程由下式给出：

式中，M为结构质量矩阵，A∞为与频率相关的附加质量矩阵，h(t)为迟滞函数，D为其他非线性阻尼矩阵，f() 为与速度相关的非线性阻尼表达式，K为结构自身恢复刚度矩阵，x、、分别为结构运动的位置、速度及加速度矢量，q为外激励载荷（包括波浪载荷、气动载荷以及系泊恢复力）。

由于非规则波的波浪频率成分复杂，而基于三维势流理论计算的附加质量矩阵与势流阻尼矩阵均与频率有关，因此无法确立某一频率下的附加质量矩阵及势流阻尼矩阵。对此，可以通过卷积积分的形式将随频率改变的附加质量矩阵与势流阻尼矩阵转化为迟滞函数进行计算，并依据四阶Runge-Kutta数值方法求解获得浮式基础的运动响应。

3 时域动力响应分析

建立气动-水动-系泊-结构耦合动力学模型，结合我国南海海域典型海况［10，15-16］与NREL 5 MW 风力机的额定作业条件［13］，对采用悬链线以及张力腿系泊的浅吃水漂浮式风力机分别进行时域动力响应分析。选用JONSWAP 谱模拟随机波浪，有义波高为6 m，谱峰周期为11.2 s，谱峰升高因子为3.3。风采用定常风进行模拟，轮毂高度处参考风速为12 m/s，环境载荷入射方向为0°。在该方向入射的环境载荷作用下，浮式风力机主要发生纵向和垂向运动，即纵荡、垂荡以及纵摇运动，故本文对这3个自由度运动响应进行分析。

3.1 浮式风力机固有周期

在无风浪且风轮保持静止状态的环境载荷下，通过给浮式基础施加一个初始位移，对纵荡、垂荡以及纵摇3个自由度进行自由衰减数值模拟。通过分析衰减周期得到采用两种系泊方式的浮式风力机基础3 个自由度的运动固有周期，如表4 所示。从表中可以看出，悬链线式浮式风力机3个自由度的固有周期均较大，张力腿式浮式风力机纵荡运动固有周期与悬链线式浮式风力机基本一致，由于张力腿系泊系统半顺应式半刚性的特点，垂荡和纵摇运动固有周期偏小。

表4 浮式风力机固有周期Table 4 Natural period of FOWT

3.2 浮式风力机的运动响应

悬链线式浮式风力机与张力腿式浮式风力机纵荡、垂荡和纵摇3个自由度的基础运动响应统计结果如表5所示，时历曲线如图5所示。

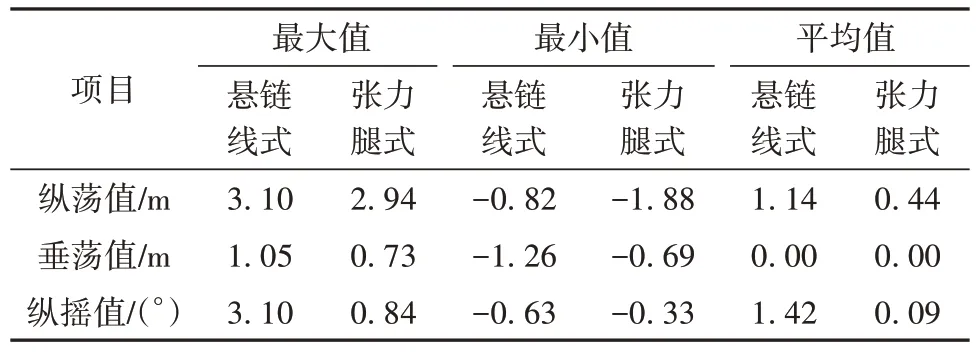
表5 浮式风力机的运动响应统计Table 5 Statistics of FOWT motion

图5 纵荡运动时历曲线与响应谱Fig.5 Time histories and spectra of surge motion

浮式风力机纵荡运动的时历曲线如图5（a）所示，运动稳定时间段内的纵荡运动响应谱如图5（b）所示。从图中可以看出，两种不同系泊方式的浮式风力机纵荡运动频率响应差异不大，都是集中在基础的固有频率和波浪频率附近，以低频运动为主，但二者的平衡位置和幅值均有所不同。结合表5的统计结果可知，采用悬链线式系泊的浮式风力机纵荡运动的平衡位置相较于采用张力腿式系泊的浮式风力机朝风浪传播方向偏移了0.7 m，张力腿式系泊浮式风力机的纵荡运动幅值比悬链线式系泊浮式风力机增加了20%。

浮式风力机垂荡运动的时历曲线如图6（a）所示，运动稳定时间段内的垂荡运动响应谱如图6（b）所示。从图中可以看出，悬链线式系泊浮式风力机的垂荡运动响应谱仍集中在固有频率和波频附近，但波频响应相较于纵荡更显著，总体以低频运动为主，而张力腿式系泊浮式风力机由于自身半顺应式半刚性的特点以及受到气动载荷的影响，其垂荡运动能量主要集中在高频区域。结合表5的统计结果可发现，悬链线式系泊浮式风力机的垂荡运动幅值为2.31 m，张力腿式系泊浮式风力机的垂荡运动幅值为1.42 m，相较于采用悬链线式系泊，采用张力腿式系泊的浮式风力机的垂荡运动幅值减小了39%。

图6 垂荡运动时历曲线与响应谱Fig.6 Time histories and spectra of heave motion

浮式风力机纵摇运动的时历曲线如图7（a）所示，运动稳定时间段内的纵摇运动响应谱如图7（b）所示。从图中可以看出，悬链线式系泊浮式风力机纵摇运动的响应谱与纵荡运动相似，均集中在固有频率与波浪频率的低频区域附近。张力腿式系泊浮式风力机的纵摇运动频率比较复杂，但最高的两个峰值出现在0.54 rad/s 和1.37 rad/s 周围，这与其垂荡运动的响应谱相似，波浪载荷、气动载荷以及张力腿式系泊半顺应半刚性的特点是造成二者类似的响应峰值的主要原因。结合表5 的统计结果可知，悬链线式系泊浮式风力机纵摇运动的平衡位置相较张力腿式系泊浮式风力机朝风浪传播方向偏移了1.33°，同时运动幅值是张力腿式系泊浮式风力机的3.2倍。

图7 纵摇运动时历曲线与响应谱Fig.7 Time histories and spectra of pitch motion

3.3 系泊缆张力响应分析

悬链线式浮式风力机与张力腿式浮式风力机2 号系泊缆的张力响应统计结果如表6 所示，时历曲线如图8所示。

表6 浮式风力机系泊缆张力响应统计Table 6 Statistics of mooring line tension of FOWT

图8 系泊缆张力时历曲线Fig.8 Time histories of the mooring line tension

从表6 的统计结果与图8 的时历曲线对比结果可以看出，张力腿式浮式风力机的系泊缆张力变化幅值与频率均大于悬链线式系泊缆，从这一角度分析，张力腿式系泊系统更易发生疲劳问题。同时值得注意的是，当浮式风力机遇到畸形波［17］等特殊海况时，采用张力腿式系泊系统将面临更大的安全风险，这对张力腿式系泊系统的安全评估与造价成本提出了更高要求。

3.4 输出功率与叶尖变形响应分析

本文选用NREL 5 MW 风力机，其控制器为传统的变速-变桨距角配置［13］。本文的计算工况选取的风速为12 m/s，超过该风力机的额定风速，此时控制器通过调节桨距角以使风力机输出功率保持在额定功率水平，防止系统过载故障，故研究采用恒功率控制策略。悬链线式浮式风力机与张力腿式浮式风力机的输出功率和风轮叶尖变形统计结果如表7所示，时历曲线如图9、图10所示。

表7 浮式风力机输出功率与叶尖变形统计Table 7 Statistics of output power and tip deflection of FOWT

图9 风力机输出功率时历曲线Fig.9 Time histories of electrical generator output

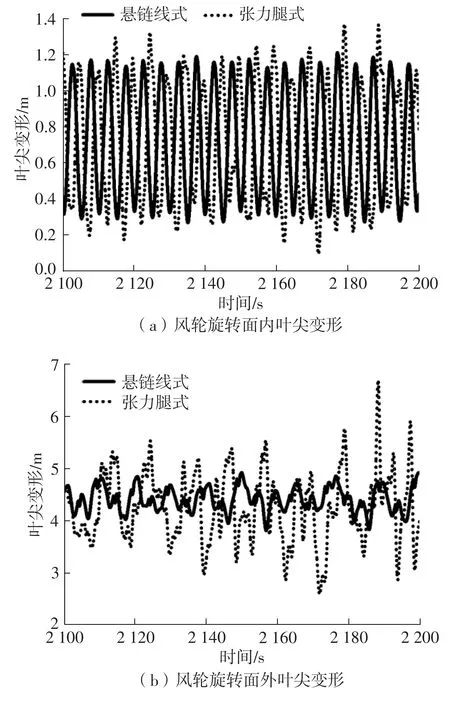
图10 叶尖变形时历曲线Fig.10 Time histories of tip deflection

从表7 的统计结果与图9 的时历曲线对比结果可以看出，在作业海况下悬链线式浮式风力机与张力腿式浮式风力机的输出功率的均值都在额定功率5 MW 附近，满足正常发电作业需求，但悬链线式浮式风力机输出功率相对更平稳。从图10 可以得知，风轮旋转平面内叶尖变形小于风轮旋转平面外叶尖变形；同时，张力腿式浮式风力机的叶尖变形幅值大于悬链线式浮式风力机。

4 结论

本文针对一种新型浮式基础的浮箱主体，根据系泊方式不同设计悬链线式与张力腿式两种浮式风力机作为研究对象，分别建立风力机-基础-系泊系统耦合动力学数值模型，并通过SESAM 软件对其作业状态下的动力响应特性进行对比研究，主要得到以下结论：

（1）水平方向上，悬链线式浮式风力机的平衡位置相对于初始位置的偏移量大于张力腿式浮式风力机，同时垂向方向上，其运动幅值亦大于张力腿式浮式风力机。

（2）在作业海况下，悬链线式浮式风力机的系泊缆张力均值和幅值均小于张力腿式浮式风力机。

（3）在作业海况下，悬链线式浮式风力机与张力腿式浮式风力机的输出功率和风轮叶尖变形的均值接近，但张力腿式风力机的数值随时间变化更大，较不稳定。

综上，对于本文提出的新型浮式基础，在作业海况下采用张力腿式的系泊方式具有更好的运动稳定性，但其系泊安全性与发电效率不如采用悬链线式的系泊方式。因此，在工程实际作业中，张力腿式系泊在运动性能上更具优势。但应该指出，张力腿筋腱的造价成本更高，而且如果遇到如畸形波等特殊海况，张力腿式系泊相较于悬链线式系泊的安全风险也更大。此外，虽然张力腿式系泊的发电效率不如采用悬链线式，但评估整体的经济性还需考虑造价、运营等成本问题，因而需要更加深入的研究。