定位传感器基站部署优化方案研究

曹昌磊，陈志达，龚小宇，洪年祥

1. 绍兴市上虞区自然资源监测中心，绍兴 312300；

2. 浙江省测绘科学技术研究院，杭州 310012

1 引 言

室内定位是一项对全球导航卫星系统在遮蔽地区的补充导航定位技术，为办公大楼、超市和室内外过渡区域的位置服务提供了极大的便利（薛伟莲等，2020)。室内定位主要采用无线通信、基站定位、惯导测量和影像导航等方式，而基站定位方式具有信号传输距离远、精度高和可行性高等优点，在多种场景中能发挥出独特优势。因此，传感器基站定位方式在城镇火灾、地震和倒塌等多种室内灾害场景下的应急导航问题处理中获得了广泛应用（黄瑞贞，2020；施志荣，2019；孙公德等，2017)。

精度衰减因子（dilution of precision，DOP)是评估导航定位精度高低的关键参数，表示测量误差与定位精度的相对几何关系。当DOP 值较大时，组网强度较低，表示在该区域使用传感器定位技术得到的位置精度较低。由于在利用伪距进行空间定位中，需要三个方向位置信息才能确定点位坐标（不对接收器的钟差进行估计)，同时需要多余观测量提高计算成果的精度，因此，通常需要4 个以上的基站观测数据才能完成空间定位。根据定位区域的环境特征，以及信号的连续、可靠、多重覆盖和探测空间最大化特点，优化传统单因子静态组网，建立兼顾多因子动态组网技术，缩短组网时间并改善综合定位精度。已有研究多集中在物流仓库、地下综采面和办公大楼等不同场景下的基站组网方式，分析在对应区域中的DOP 分布情况，讨论基站几何布设对定位误差的影响（何琦敏和王坚，2017；王宁等，2020；杨燈等，2020)。但这些布设方案过于理想化，仅考虑单个因素DOP 的误差影响，忽略信号连续和重叠等多因素作用。其中，这些因素导致基站组网优化本质上是一个组合优化问题。因此，在实际组网过程中，上述方法通常难以满足最优布设基站要求。

近些年，有不少研究提出使用遗传算法优化基站组网布设，对传统的布设方案进行优化（何琦敏等，2017；Wang 等，2022；周宇泰等，2022)。遗传算法是一种全局寻优算法，最早由美国科学家John Holland 在20 世纪70 年代提出，由于算法的全局搜索能力和稳健性特点，在解决较为复杂的组合优化问题上能够较快地获得优化结果（刘修宇等，2021；缑慧娟和杨成龙，2020)。然而，这些方法中没有考虑信号的通信距离与覆盖区域的几何关系及相关的应急条件。因此，本文以改进的自适应遗传算法对基站组网进行优化，综合考虑信号的连续、可靠、多重覆盖和探测空间最大化特征，分析优化方案后的组网强度，为应急救援等情况下的定位组网提供参考依据。

2 组网部署方法

按照观测模式分类，使用定位传感器观测数据进行导航定位的方式主要有双向测距（two way ranging, TWR)模式、时间到达（time of arrival，TOA)模式和时间到达差（time difference of arrival，TDOA)模式。其中，TOA 算法具有精度较高、定位收敛和基站构建简单优势，因此，常用于基站测距定位的实践应用。

2.1 TOA 定位原理简述

TOA 是一种通过测量终端至基站之间的信号传输距离推测终端位置的定位方法，根据基站发送至终端接收电磁波信号的传输时间计算两点之间距离，建立基站与终端距离的观测方程。对于终端的空间位置共三个未知参数，因此接收到至少3 个基站的信号数据，即可实现空间定位。根据最小二乘准则和间接平差原理可知（刘大杰等，2003)：

式中，P为观测值权阵，由于观测值均为相对独立，因此，可设为单位阵；x为待求参数的估计值；B为x的雅可比矩阵；f为残差项；Qxx为待求参数的协因数阵；Q为观测值协因数阵，满足P=Q-1。由此，可得到x的协因数阵Qxx。假设定位传感器的测距单位中误差为δ0，即有x的方差阵为Dxx=δ0Qxx。

2.2 精度衰减因子

用于估计二维平面的精度可用HDOP 表示：

用于估计高程方向的精度可用VDOP 表示：

用于估计三维空间的精度可用PDOP 表示：

式中，xσ、yσ、zσ为坐标在三个方向上的误差；0σ为传感器测距中误差。假定信号在传输过程中的定位传感器单位测距误差保持不变，DOP 将由基站和终端位置的几何关系确定，是一个无量纲值。式(2)～式(4)表明，当待求坐标协因数阵上的对角线元素值较大时，DOP 较大，表示点位的定位精度较差。因此，根据HDOP、VDOP 和PDOP 值所代表的区域二维、高程和三维精度，从而可评估最终组网的稳健性。

2.3 基站组网的基本准则

在一个已知的封闭空间中，基站数量和部署形式（矩形、星形和菱形)将直接影响空间定位精度。由于实际室场景中存在较为密集的人流和物体，同时需要考虑封闭空间的几何构造，因此，需要通过分析多种部署方案的实验结果，选择最佳的布设方案以达到相应的定位要求。基站的信号传输距离通常有限，为保证信号持续传输，必须保证信号的连续性。由于采用传感器定位技术进行定位需要同时接收多个基站的信号，因此，基站的布设方式应满足一定的区域重叠。为了进一步扩大研究区域的范围，应使用一定数量的基站以保证定位区域最大化。此外，为了保证连续跟踪的终端目标精度达到相应要求，避免错误定位，要求组网方式具有一定可靠性。综上，基站组网的布设方式需要满足信号连续性、多重信号覆盖、责任区域最大化、可靠性原则（陈秉试，2021)。由于基站的部署受到上述几种因素的影响，因此，基站的部署优化问题是一种组合优化问题。针对每一种组网准则，应满足如下特点。

1)信号连续性

假定基站的最大通信距离为d，基站至终端的距离为l，为了确保基站能够连续接收无线信号完成定位工作，要求l＜d。

2)多重信号覆盖

假定所有的基站数量为k，完成定位工作的最少接收基站数为N0：

3)可靠性

假定任务要求点位的DOP 阈值为FDOP，为了保证精度达到要求，即有待定点DOP＜FDOP。

4)探测区域最大化

网络的覆盖范围直接影响区域的严密程度和探测能力。在保证覆盖层数的条件下，同时满足覆盖区域尽量最大。

为了保证待探测区域中的DOP 值整体表现较小，定位盲点个数达到最少的目标，满足相关部门对不同区域的精度设计要求。通过一定数量的基站，并将基站分布在区域周围，达到上述条件要求，可建立相应的目标函数并对其量化：

式中，m为不同区域的类型数目；ni为选取的有限区域点（用于计算整体DOP)数量；ki为区域差异性引起DOPj的权重系数（重点定位区域系数比一般定位区域系数大)；num(DOPi＞FDOP)为指定区域i中的盲点数量（即盲点面积)，即区域内大于FDOP的点数（DOP 值较大时，定位精度低)；wi为对应的num(DOPi＞FDOP)权重系数。

3 基于改进的自适应遗传算法基站部署

通过基站的组网部署原理可知，优化基站网络的性能需要实现目标函数式（6)达到最小完成，本质上是一种组合优化问题（刘永信等，2021)。目前解决组合优化问题的算法主要有多项式时间算法（曲明等，2022)、近似算法（廖玉婕，2022)、启发式搜索算法（梅志虎和唐志波，2023)和遗传算法（杨雄和吴东，2021)等。多项式时间算法、近似算法和启发式算法普遍存在枚举数量过多、时间效率低、算法计算复杂度高和与最优解的偏差较大等问题（但开和段隆振，2022；李豪等，2023；鄢伦等，2023)。遗传算法是一种高度并行、随机且具备自适应能力的迭代方法，能够有效避免陷入局部最优，最大化缩短与最优结果的差距（李作山等，2019；文传奇等，2023；方占萍等，2023)。但传统遗传算法也存在对初始解与遗传算子设计依赖性和局部收敛性等缺点。为了克服上述问题，本文采用改进的自适应遗传算法用于基站组网方案设计。算法需要对基站的位置坐标进行编码，经过种群配对与迭代计算后，提取最佳基站坐标解集。具体方法为，首先，需要分析定位区域的空间环境条件，作为参数的输入源，以多种常用的组网方式（菱形或方形布设等)形成初步方案；其次，结合改良圈算法优化初步方案，求得初始方案适应度，并选择改良后的基站方案开始进行迭代运算；最后，基于改进的自适应遗传算法生产新的子代解集，并对子代解集进行适应度优化，提高算法解算效率。如图1 所示。

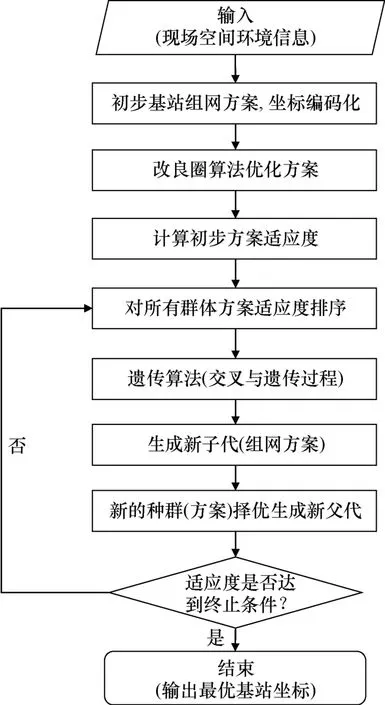
图1 基于改进的自适应遗传算法基站部署方案Fig.1 Base station deployment plan based on improved adaptive genetic algorithm

1)染色体编码

在使用遗传算法时，需要先将解算空间的具体参数转换为染色体表示，也称为编码。编码方式主要有二进制编码法、实数编码法、排列编码法和复数编码法等方式。在满足完备性、健全性和非冗余性的前提下，二进制编码结构简单，且便于遗传和变异操作，在遗传算法中应用最广。因此，本文采用二进制编码方式开展后续研究工作。

2)种群的初代优化

遗传算法的解空间主要由种群数目确定，而初始种群决定了算法的初始解及收敛效率。为了保证取得最优解，初始种群应具有一定的规模，需要避免由于大规模搜索空间引起的遗传算法收敛时间过长的问题。同时，初始种群的优劣也直接影响到结果的准确性和算法效率。本文采用Hamilton 改良圈算法（薛慧和许苗峰，2020)对初始种群进行优化，以获得较好的父代。

3)交叉与变异

改进的自适应遗传算法染色体交叉配对主要采用“门当户对”的方式进行，也就是根据样本的适应度大小确定种群优劣排序，适应度小的父本与适应度小的父本交配，适应度大的父本与适应度大的父本交配。染色体交叉点的节点位置根据Logistic函数序列确定，在选定的父代样本指定位置上完成上述交叉操作。

在算法实现中，可以预先指定交叉概率值Pj（0～1)。一般情况下，当所有父本均存在交叉行为时，概率值为1，反之不发生则概率值为0，通常情况概率值较大。每一次实现交叉行为算法时，先产生一个区间大小为0～1 均匀分布的随机数，当概率值小于Pj时，则在对应的序列点上进行交叉操作，反之则不进行操作。

此外，与交叉操作类似，在变异操作上可先从交叉后的个体中选择变异个体，预先设定一个介于0～1 的变异概率值Pb，为了保证收敛过程平稳进行，因此，通常变异概率较小，在规定父本的容量N的条件下，则发生变异体的个数Nb=Pb·N。

4)自适应优化

为了提升子代最优解的质量，减小局部最优解的概率，可对遗传变异概率进行自适应改正，避免在变异函数时间序列大空间范围内进行搜索时陷入局部极值，因此，采用式（7)、式（8)进行修正：

式中，P j0、Pb0分别为设置的初代交叉和变异概率值；α、β分别为区间[0，1]的常数；fj、fb分别为父代交叉和变异样本中的最大适应度值；faver、fmax分别为全体样本的平均和最大适应度。使用遗传算法自适应函数式（6)计算目标函数值（适应度值为该值相反数)，当该值越大时，表示此时的个体适应度越小，组网效果较差，反之组网效果较好。

4 模拟实验与结果分析

4.1 模拟实验参数预设值

本文以模拟仿真的多层球形体育馆为例，假定球体的最底层圆直径为200 m，共分为四类不同高度层的重点定位区域。其中，四类不同高度层的区域分别为0～5 m、5～10 m、10～15 m 和15～20 m，基站信号的最大传输距离为250 m。考虑两种基站布设方案：一是存在固定站（位于顶端)，其余为流动站（位于区域的外侧地面)；二是均为流动站（位于区域的外侧地面)。其中，地面站点的基站伸缩长度不高于2 m。图2 为基站布设方案示意图。

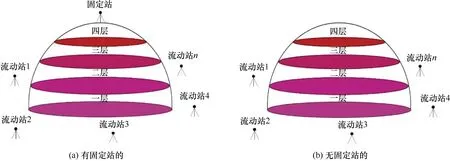
图2 基站布设方案示意图Fig.2 Base station deployment plan

改进的自适应遗传算法参数设置如下：初始样本大小为N=50，初始交叉和变异概率值Pj0、Pb0分别为0.95 和0.1；在适应度函数中，最大容忍的FDOP值为12，四个区域的DOP 加权值为k={1，2，3，4}，四个区域DOP 越值的加权值为w={1，2，3，4}，即随着楼层高度增加，高层区域为重点定位区域。以各个流动基站坐标为待求参数，进行编码，设置迭代次数为50 次，基于组网部署基本准则的整体目标函数，即式（6)值小于10 或次数达到最大迭代次数即可停止运算，输出最优基站坐标序列。

4.2 结果分析

使用改进的自适应遗传算法对两种布设方案的基站部署进行优化。下表为两种方案和改变基站数量后，各层的平均HDOP、VDOP 和PDOP，以及适应度函数值，如表1 所示。

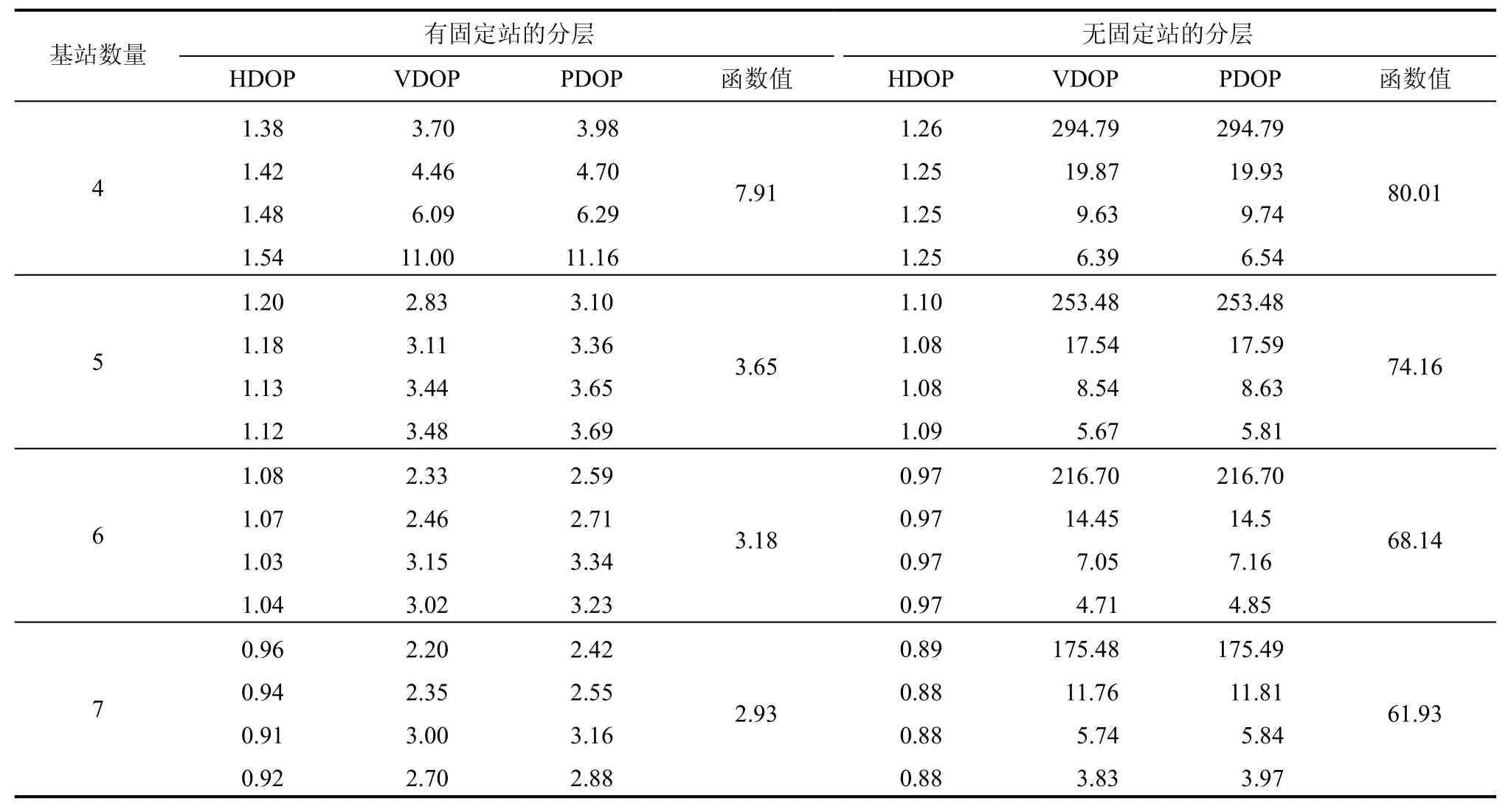
表1 改进的自适应遗传算法运算结果Tab.1 Calculation results of improved adaptive genetic algorithm

由表1 可知，设立的固定站点能够有效减小VDOP 和PDOP，改善在高程方向的精度，不使用固定站的情况下，两者的HDOP 基本相当。同时，随着基站数量增加，终端观测条件得到一定改善，当基站数量从4 个增加到7 个时，在固定站方案中，HDOP、VDOP 和PDOP 分别减小20.4%、27.4%、35.9%，49.0%、56.5%、59.4%，47.1%、54.5%、57.8%；在无固定站方案中，HDOP、VDOP 和PDOP分别减小了13.1%、22.5%、29.5%，13.7%、26.5%、40.4%，13.7%、26.5%、40.4%。此外，随着高度增加，VDOP 和PDOP 呈现增减趋势，在固定站方案中，VDOP 和PDOP 呈现增大的趋势，随着基站数量增加后，这种趋势不明显；在无固定站方案中，VDOP 和PDOP 呈现减小的趋势。分析出现上述情况的原因主要是，在固定站方案中，由于基站数目增加后，观测条件得到了极大的改善，即使在恶劣的网络结构条件下，仍然能够保持较高的精度；而针对无固定站方案中，由于所有站点位于地面，此时低层的空间高度角基本趋于0°，整体观测条件较差，随着高度增加，高度角的改善使得位于高层的观测条件达到最佳。

综上所述，基站数量由4 到5 时，组网效果显著提升，而继续增加基站数量后，DOP 值没有明显降低，因此，在兼顾基站成本情况下，选择5 个基站更加符合大多数的工程定位应用需求。为了进一步分析组网方式的空间位置精度分布特征，以组网综合情况最佳的5 个基站（具备固定站)方案为例，绘制了分层的PDOP 等值线图，如图3 所示。

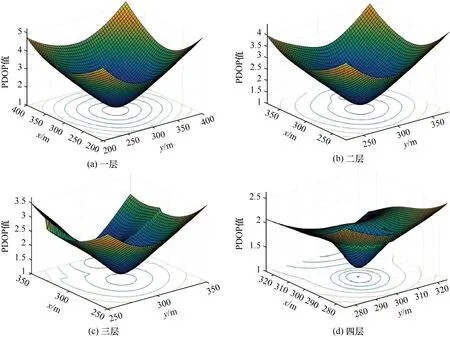
图3 5 个基站布设方案的PDOP 空间分布Fig.3 Spatial distribution of PDOP for 5 base station deployment plans

随着楼层增加，PDOP 整体呈现减小趋势，分布由单一中心区域PDOP 最小对称结构变为多中心最小结构，在考虑整体定位范围前提下，重点兼顾高楼层定位区域的精度。因此，在解决组网定位中的基站布设问题时，需要综合考虑固定站与底部流动站和定位区域高度的关系，保证应急情况下作业人员进入室内搜救路线设计安排。

5 结 论

本文介绍了定位传感器组网部署的优化方案原理与设计，以模拟的多层球形体育馆仿真实验为例，利用改进的自适应遗传算法对基站组网设计进行优化。分别讨论有固定基站和无固定基站的组网部署方式的DOP 分布，分析了基站数量对基站组网的性能影响。结果表明，在建筑物顶端设立固定站能够有效改善VDOP 和PDOP，针对一般的二维定位可不需设立固定站，采用无固定站的方式具有较好的平面定位性能；随着基站数量的增加，DOP值得到一定程度的改善，但改进效果越来越不明显。因此，在达到定位条件的情况下，可以综合考虑基站组网的成本，减少基站的数量，在使用4 个流动站和1 个固定站的方案下，可以使最终的综合效益达到最高，同时定位精度可向重点定位区域方向倾斜，为相关的组网布设提供参考依据。