虚拟地理环境中全景图深度信息恢复与应用
徐铮,李锋,蒲泓亦,卢雪
1. 信息工程大学 地理空间信息学院,郑州 450000;
2. 92292 部队,青岛 266000
1 引 言
虚拟地理环境(virtual geographic environment,VGE)是真实地理环境在计算机中的逼真模拟和数字化表达(龚建华等,2010;林珲等,2013),通过数字地表模型、遥感影像、地物模型等测绘数据构建的三维虚拟场景,用户可以借助VR 设备在三维虚拟场景中沉浸式地体验地理现象并开展地理实验(谭力恒等,2019)。全景图是将全景相机固定在某一位置,通过旋转相机拍摄多张照片拼接成全景图像(钟力等,1999),能够提供与现实世界一致的全视野视觉体验。空中全景图(周智勇和丁玉兰,2016)是在高空拍摄的全景图像,可提供高空俯视、遨游天空的体验感。伴随无人机和全景获取技术的快速发展,众源全景图像数量剧增。众源全景图像能够记录大量的目标内容,包括重要城市、港口、出海口等。目前,空中全景图像和虚拟地理环境融合的应用日趋增加,空中全景图像已经成为虚拟地理环境重要的组成部分。由于全景图像成像过程中缺失深度信息,仅能提供用户真实的观察感,无法提供深度信息,极大限制了虚拟地理环境中空中全景图像的应用。
国内外学者对全景图像深度信息获取和处理做了大量的研究。Fangi 和Nardinocchi(2013)首先提出球面摄影测量的概念,使用空间后方交会法解算球面全景图像的外方位元素,获取深度信息,主要用于历史文物和建筑记录。启发于传统图像多视图立体几何原理,大量研究采用多目(n≥2)视觉全景图像方法获取空间点到镜头中心的距离。例如,研究设计了基于双鱼眼镜头的球面立体视觉系统,引入鱼眼球图像的视差从而获取深度信息,该方法广泛应用于远距离目标的精确测量、虚拟环境系统仿真等领域(Li,2008;龙帮强等,2015;高兴烨等,2016;黎晓东等,2017)。Laganière 和Kangni(2010)使用立方投影处理球面全景图像,从多个立方体图像获取目标点深度信息。Liu 等(2020)直接建立双球面投影的几何关系,并与近景摄影测量相对定向的转换参数进行比较,证明方法可行。随后,多传感器组合获取全景图像深度信息的方法逐渐崭露头角。季顺平和史云(2014)建立了多镜头组合全景相机成像模型,将其与GPS/ IMU(全球定位系统/惯性测量单元)数据结合,用于光束法平差(邓非等,2016)、位姿估计(闫利和王奕丹,2017)和定向,实现全景测量(谢东海等,2017)。上述方法中,球面全景摄影测量方法精度有限,一般用于浅深度场景的深度信息获取;多目立体视觉全景深度信息获取方法需要计划多个摄站;多传感器组合获取全景图像深度信息的方法成本较高。
本文结合传统测绘数据,以虚拟地理环境为空间,进行球面全景图像深度信息获取。保证一定精度的同时,发挥全景图像和虚拟地理环境的融合特点。在虚拟地理环境中设计基于深度信息的全景图空间分析量算模型,解决空中全景图不支持空间分析量算的问题,并丰富虚拟地理环境应用,深化用户环境认知。
2 全景图深度信息恢复与应用流程
海量的众源全景图数据为环境勘察提供了一个新的途径,利用空中全景图进行室外大场景环境勘察,能够减少地物遮挡,扩大观察范围。当前全景图大多是二维图像,缺乏深度信息。利用射线求交法计算像点的深度信息,使图像从二维平面转化为三维立体,实现基于全景图的分析量算,为分析全景图空间关系提供有效支撑。
本文采用高精度数字地表模型和倾斜摄影模型构建精确的三维虚拟场景,为全景图深度信息恢复提供准确源数据。分别在全景图和虚拟地理环境中选取匹配的特征点,通过后方交会法解算相机位姿信息,将精确的相机位姿和地理环境进行配准,计算全景图深度信息并设计空间分析量算模型,实现全景图空间分析量算功能。如图1 所示,主要分为四个阶段。
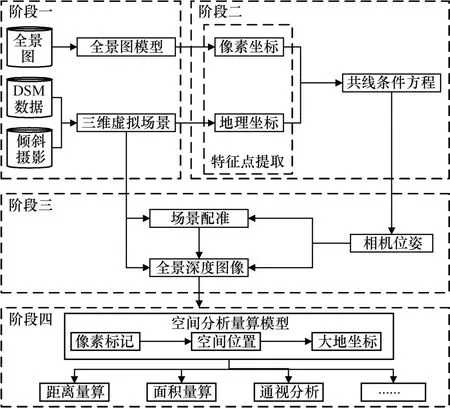
图1 全景图深度信息恢复与应用流程图Fig.1 Workflow diagram for panorama depth information recovery and application
阶段一,利用高精度的数字表面模型(digital surface model,DSM)、倾斜摄影三维模型和全景图,构建目标区域虚拟地理环境。
阶段二,选取多组特征点,通过投影变换计算全景图特征点的像素坐标,利用坐标变换计算虚拟地理环境中对应特征点的地理坐标,根据改进的后方交会算法解算全景相机的拍摄参数。
阶段三,将相机与虚拟地理环境配准,相机位置点和全景图像点构成射线与三维虚拟场景中地形模型射线求交,计算全景图深度图像。
阶段四,设计空间分析量算模型,通过将全景图像点的像素坐标转化为地理坐标实现距离、面积、方位角等分析量算功能,并将计算结果实时显示。
3 众源全景图数据处理与虚拟地理环境构建
3.1 众源全景图数据处理
众源全景图数据是大量非专业人员利用无人机、智能手机等采集的带有地理标识的全景数据,通过标注处理后上传到开放式数据共享平台(冉飞鹏,2015)。与实拍空中全景影像不同,众源空中全景图一般仅含有拍摄地点所在县市或景区的名称及位置属性,缺少拍摄参数,可以利用众源地理数据网站提供的API 接口获取目标区域的全景图数据(单杰等,2014;葛洪涛,2015)。首先,将采集的原始图像数据进行分类整理,剔除不符合要求的图像;其次,对图像预处理,消除图像中异常的色彩和亮度;最后,对图像进行拼接处理(王飞等,2019),得到长宽比为2∶1 的全景图。
3.2 虚拟地理环境构建
构建三维场景不仅要集成多源数据,还需要场景渲染和相机控制。三维场景采用树状的层次结构组织,利用影像数据和数字高程模型,以纵向分层、横向分块的方式加载数据,生成全球范围内的地形环境。针对目标区域,采用高精度的数字表面模型和倾斜摄影三维模型数据构建目标区域三维虚拟场景,同时在场景中添加相机视角,实现全方位任意姿态漫游三维虚拟场景。
将全景图技术与三维虚拟场景相结合,构建融合全景图的虚拟地理环境(李科等,2013)。根据目标区域全景图的拍摄范围,估计全景相机拍摄位姿。同时在虚拟地理环境中添加标记符号,并在标记符号上添加全景图链接,实现在虚拟地理环境与全景图之间任意跳转,在三维场景中勘察目标区域。
4 基于后方交会的全景拍摄参数解算
4.1 球面全景建模
全景图展现的场景是以相机为中心,周围360°的全景信息。像素坐标系是计算机内部数字图像使用的一种坐标系,数字图像以二维数组的方式存储。将全景图上的某点映射到等经纬度图上,需要将全景图像素坐标转化为经纬坐标。
如图2 所示,直角坐标系O-UV中点O为坐标原点,l为全景图长度,w为全景图宽度。直角坐标系O'-U'V'用作相机内部成像坐标系。假设O'为影像中心原点,设全景图上任意像点(u,v)在坐标系O'-U'V'为(x',y'),那么两个坐标系的转换关系为

图2 全景图球面建模Fig.2 Panoramic sphere modeling
平面全景图长宽比为2∶1,对平面全景图进行球面建模,即l对应球面经度[-π,π],w对应球面纬度[-π/2,π/2],O-UV是像素坐标系,P'为全景图像上任意一点,球心Os为原点,X轴指向平面影像中心O'在球面上的映射点,Y轴垂直于X轴构成球赤道平面,Z轴与X轴、Y轴构成右手坐标系,建立球空间坐标系Os-XYZ,Ps为P'在球面上的对应点。根据全景图与等经纬度图像的对应关系,可得全景图上点P'在球面模型上的对应点Ps的经度PLo和纬度PLa分别为
4.2 相机拍摄参数解算
根据相机位置点、全景图像点构成的射线与数字地表模型相交,可建立共线方程(陈义,2004),解算全景相机拍摄参数,公式为
式中,(x,y)为像点的像平面坐标;f为相机焦距;(X,Y,Z)为射线与数字地表模型的交点;(Xs,Ys,Zs)和(a1,b1,c1,a2,b2,c2,a3,b3,c3)为要解算的相机拍摄参数。但是球面上像点的纵坐标随着像点的球面纬度变化而变化,利用式(3)求解相机拍摄参数会增大误差。为了减少解算相机拍摄参数误差,提高解算效率,简化模型计算复杂度,利用透视投影将球面全景图映射到虚拟平面,得到虚拟平面像点(图3)。
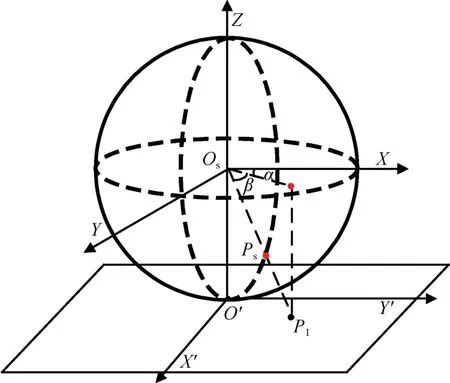
图3 球面全景映射Fig.3 Spherical panoramic mapping
设球坐标系Z轴负方向与虚拟平面相交于O',过O'且垂直于Z轴的平面XO'Y,球面上像点Ps,和虚拟平面的映射点P1(x,y,z)连线与虚拟平面相交于点P1,那么球面上任意一点Ps与虚拟平面上对应点P1的映射关系为
由图3 可知,球面全景图像位姿决定虚拟平面位姿,那么采用平面空间后方交会法解算虚拟平面外方位元素即可计算出全景相机的拍摄参数。
5 全景图深度信息恢复与空间分析应用
5.1 计算相机射线与地形交点
众源空中全景图一般为二维图像,缺乏深度信息,降低了用户环境感知能力。为了恢复全景图的深度信息,本文依据光线直线传播原理,提出相机位置点—全景图像点—虚拟地面点三点共线法求解像点与对应地面点的距离,近似地表示为该像点的深度信息。在虚拟地理环境中,根据射线求交法(张宗佩等,2015),计算全景深度图,计算图中像点与对应地面点的距离,地面点为全景图相机位置点与像点所组成的射线和地形模型的交点(图4)。其中,C为全景图相机位置点;为全景图中像点;△P1P2P3为某一地形图元;P为射线CC1与三角形图元P1P2P3的交点;CP为光线路径;n12为与组成的平面的法向量;C'为平移经过三角图元顶点P1后C对应的新位置。研究地形上的三角图元上的落点为P,则参量值方程为
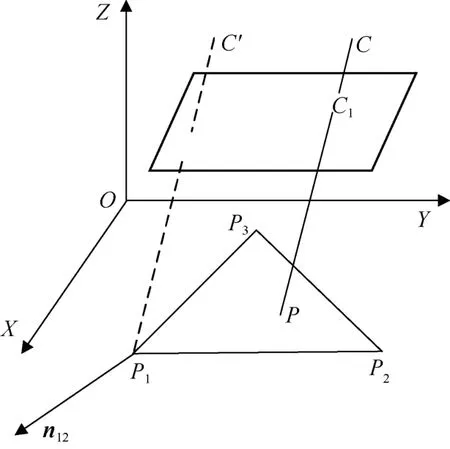
图4 三角图元求交结构Fig.4 Find intersection structure of trigonometric graph elements
射线CP与三角图元满足以下任意一种情况有交点,即相交:D312≥0,Dc12>0,D312>Dc12,Dc12≠0;D312≥0,Dc12>0,D312>Dc12,Dc12=0,D312≠0;D312<0,Dc12<0,Dc12>D312,Dc12≠0;D312<0,Dc12<0,Dc12>D312,Dc12=0,D312≠0。
同理,对三角图元的另外两种组合也按照上述方法进行判断,方程为
如果三种组合判断结束后都有交点,则说明P点在△P1P2P3上。
5.2 解算全景图像点的深度值
根据前文所述方法可以得到三种类型组合所有的值。如果Dc12=0,则r3=0,否则r3=Dc12/D312;如果Dc13=0,则r2=0,否则r2=Dc13/D213;如果Dc23=0,则r1=0,否则r1=Dc23/D123。根据计算得到的三个因子r1、r2、r3,对其进行归一化处理:
如果Rt=0,则表明射线CP与三角图元平行,不存在真正的交点;否则表明有交点,交点P的坐标为
那么该像点C1的深度值可记为
式中,(xC,yC,z C)为C点坐标;(xP,yP,z P)为P点坐标。同理,可求出全景图中所有像点的深度值,生成全景深度图。
5.3 基于全景图深度信息的空间分析量算
虚拟地理环境中,基于空中全景图的分析与量算应用是虚拟地理环境应用的重要部分。不同于在虚拟地表,空中全景图能够提供侧面等内容,空间上拓展了量算与分析的范围。同时,基于空中全景图的分析与量算能够直接在全景图上实施,避免人工确定全景图目标点与虚拟地面目标点,再由对目标地面点或区域进行量算的过程,提高用户沉浸感。针对空中全景图成像特点,设计空间分析量算模型,实现基于空中全景图的距离、面积、方位角等空间分析量算功能。通过选取全景图像点获得像素坐标,根据该点的深度信息计算地理坐标,代入相关算法模型完成空间分析量算。
如图5 所示,以相机位置为原点Os,根据相机拍摄参数建立像空间坐标系,由全景深度图可知全景图像点P1、P2、P3的深度值分别为d1、d2、d3、计算出P1′、P2′、P3′的地理坐标,即可求出像点P1、P2、P3组成的实际区域面积。

图5 空间分析量算模型Fig.5 Spatial analysis volume calculation model
设球面上点P的像素坐标为(xi,yi,zi),那么像点P的空间向量为
像点P对应的地面点P'在像空间坐标系中的相对坐标为
式中,di为像点P的深度值;记P'在空间大地直角坐标系中的坐标为Pg,那么该像点对应的地理坐标为
式中,Os为相机在空间大地直角坐标系中的位置;R为大地空间直角坐标系转换到像空间坐标系的旋转矩阵。同理,可以计算出P1、P2、P3对应的地面点P1′、P2′、P3′地理坐标,实现距离、面积、方位角等空间分析量算功能,并将处理结果在全景图上可视化显示。
6 实验与分析
本文以河南省登封市纸坊水库地区作为实验场地,采用数据精度为0.3 m 的数字地表模型和0.1 m 的倾斜摄影三维模型数据,结合全国底层遥感影像数据,搭建基于OSG Earth 的虚拟地理环境,通过“720 云”等网站获取纸坊水库高空多张影像,处理成分辨率为8192 像素×4096 像素的全景图,在全景图中找出多个具有明显标志的像点为特征点,根据球面建模原理,计算倾斜摄影模型中与全景图特征点对应的地面点(图6)。
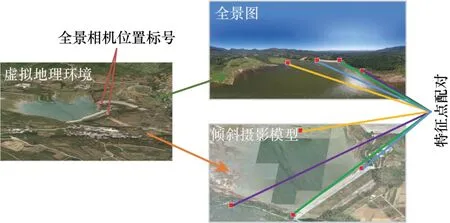
图6 特征点提取Fig.6 Feature point extraction
在全景图中标记有明显特征的像点,并在虚拟地理环境中计算对应特征点的地理坐标(表1)。

表1 特征点对坐标Tab.1 Coordinates of characteristic points
为了减小误差,选取多组数据解算全景图的外方位元素,解算得:Xs=-20.87,Ys=23.17,Zs=67.49,t=-3.45487354,w=-1.06735462,k=53.46258432。
转换后可得拍摄相机的地理坐标(113.105854°E,34.525095°N,509m),并更新拍摄相机标记在虚拟地理环境中的位置。根据全景相机在虚拟地理环境中的位姿,结合射线求交法,利用相机位置和全景图像点位置构成的射线与虚拟地理环境的交点,计算像点的深度值,生成全景深度图(图7),其中,全景深度图的长l和宽w,与空中全景图的大小相同。通过手动操作,在全景图中选取像点,系统根据像点坐标获取在虚拟环境中对应的地面点坐标。

图7 全景图标记点地理坐标误差分析Fig.7 Analysis of geographical coordinate error of marking points in panorama
为了验证实验方法的有效性,根据地形环境特点在全景图中选取15 个标记点,计算各标记点的像素坐标,结合全景深度图计算虚拟地理环境中所有标记点的地理坐标,记为实验值。同时,通过传统测绘方法获取所有标记点的地理坐标,记为标准值。标记点深度值在[0,100]、[100,200]、[200,300]、[300,1000]范围内时,相对误差分别为3.7%~8.7%、3.9%~17%、11.9%~17.5%、14.7%~26.2%。通过计算结果对比,在空中全景图中,全景相机拍摄的正下方近处场景图像像素比远处场景图像像素的深度信息计算结果误差小,而且误差会随着相机仰角的增大而增大,造成误差的主要原因是全景图像拼接、全景相机位姿解算及射线与地形相交产生的误差。
根据实验结果,为了较少误差带来的影响,提高计算结果的可靠性,本文选择全景相机位置点附近区域进行分析量算(图8),在全景图中选择目标点,计算目标点的像素坐标和地理坐标,利用空间分析量算模型对目标点进行计算,并在全景图上实时显示计算结果,其误差小于10%,能够辅助分析空中全景图中目标点的空间关系,深化用户环境感知。

图8 基于全景图的分析量算Fig.8 Analysis based on panorama
结果表明,本文提出的虚拟地理环境中全景图深度信息恢复与应用的研究具有一定的可行性,有助于提高对空中全景图的空间关系认知,扩展了空中全景图像与虚拟地理环境的应用途径,提供了一种对陌生地域的环境勘察方法。
7 结 论
全景图已成为环境勘察的重要手段,是构建虚拟地理环境的重要数据来源,本文将虚拟地理环境和全景图技术相结合,通过改进的后方交会算法解算相机拍摄参数,基于射线求交法恢复全景图的深度信息,实现了基于全景图的空间分析量算功能。本方法可为构建一个地理空间数据与全景图融合显示,具有可量测、可交互的虚拟地理环境提供一个有效途径。下一步可以深入分析由于拍摄距离改变引起景深变化,从而导致全景图像点表示的地理空间位置产生差异这一问题。

