织物悬垂性能的各向差异性研究

宋委娜　刘成霞

摘 要：为研究织物悬垂性能的各向差异性，对传统的伞式测量法进行改进。选取15种常见织物，采用XDP-1织物悬垂仪对织物0°、90°、45°和135° 4个方向的悬垂性进行测试并获取悬垂图像；基于所得图像提出最大展宽、投影面积和悬垂系数3个新指标；最后分析织物各向悬垂性与弯曲长度和抗弯刚度的关系。结果发现：这3个新指标与弯曲长度和抗弯刚度均具有较好的相关性；织物硬挺的方向易形成波峰，柔软的方向易形成波谷，织物某方向的悬垂性越好，越易弯曲，该方向的抗弯能力越小。这表明通过一块圆形试样的悬垂投影可以预估织物某方向的弯曲性能，利用改进的伞式法可以测量织物悬垂性能的各向差异性。

关键词：织物；悬垂系数；最大展宽；投影面积；悬垂性；弯曲性

中图分类号：TS102.9 文献标志码：A 文章编号：1009-265X（2023）06-0160-07

悬垂性是指织物因自重而下垂的性能，是一个影响面料视觉风格、美学舒适性的重要指标［1］。因此准确测试与评价织物的悬垂性，具有重要的理论和实际意义［2］。客观评价织物的悬垂性，是国内外众多学者极力想解决的问题［3］。

织物悬垂性的测试方法有多种，其中伞式测量法是国际上最通用的方法［4］。随着科技的发展，许多学者相继提出了新的悬垂性测试方法，如倒Ω法［5］、M型测试法［6］、仰视投影法［7］等。此外，悬垂性的评价指标［8］也是重要的研究内容。最常见的评价指标是悬垂系数，波纹数、波峰幅值、波峰夹角、柔性刚度、弯曲长度、图像占有率［9］等也被广泛应用［10］。

在目前涉及悬垂性的研究中，伞式测量法只能用来测量织物整体的悬垂性能。然而，由于织物经纬密不同或结构不同，同一织物在不同方向的悬垂性也存在显著差异，简称悬垂各向差异性。伞式测量法是否可以表征织物悬垂性能的各向差异性尚未可知。因此，本文尝试通过对传统的伞式测量法加以改进，在测试前标明织物的丝缕方向，通过分析实验获取的悬垂图像，提取最大展宽、投影面积和悬垂系数3个新指标，来探索这一问题。

1 实 验

1.1 试样的选取

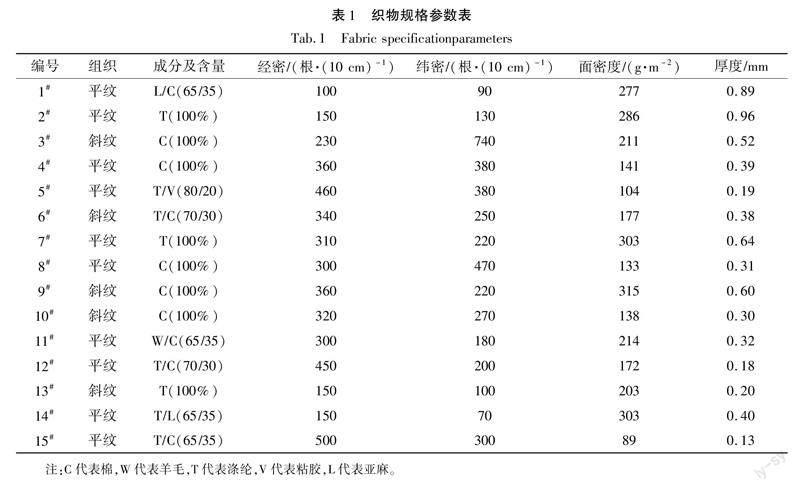
选取市场上常见的15种织物，其成分结构各不相同，具体规格参数如表1所示。

1.2 织物悬垂性测试

采用XDP-1织物悬垂仪（上海新纤仪器有限公司）对织物悬垂性进行测试，并获取悬垂图像。该仪器采用伞式测量法，将圆形试样（直径为240 mm）置于托盘（直径为120 mm）上，开始测试后，试样和托盘匀速升起，试样因自重而下垂，并呈现悬挂状态，测试完毕后即可看到织物的悬垂投影图。本文对测试过程进行了改进：

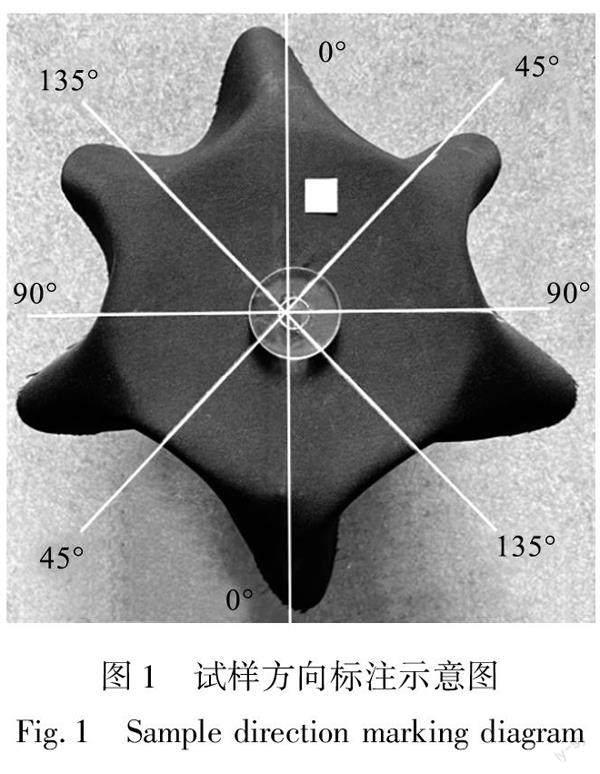
a）裁剪试样前，对织物用量角器进行方向测量，且用记号笔标明4个方向：0°（经向）、90°（纬向）、45°和135°。

b）将织物试样置于托盘上，确保固定，使其0°始终为竖直方向。试样方向标注方式示意图如图1所示。

c）在织物上方放置边长为1 cm的正方形卡纸，用作后续处理的参照物。

所有实验均在标准大气环境中进行。

1.3 指标构建

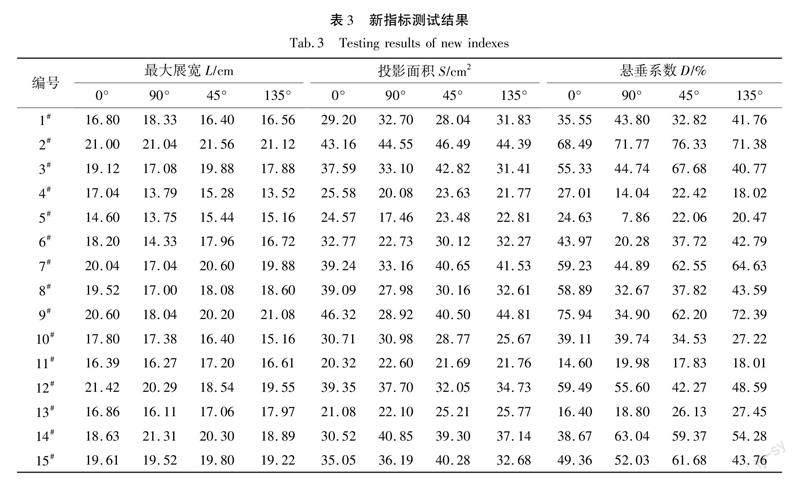
用Matlab软件读取悬垂图像，并对其进行灰度化、二值化、形态学等处理，然后用bwlabel函数、regionprops函数以及imtool函数分别计算投影面积S和最大展宽L，根据参照物面积和长度求出被测试样的新指标值。新指标含义如下：

a）最大展宽L：根据试样的悬垂图像，提取试样每个方向两端展开的最大距离，cm。织物悬垂特征指标最大展宽如图2（a）所示。

b）投影面积S：将试样4个方向等角划分（每个方向的角度为45°），形成不规则区域的投影面积，织物悬垂特征指标投影面积如图2（b）所示。以图2（b）中S经为例，分别取图1中的0°与45°以及0°与135°的角平分线，两条角平分线与织物投影的外轮廓围面积即为S经。

c）各区域的悬垂系数D：按照步骤b）中的分区方法，将织物的悬垂投影图像分为8个区域，如图2（b）所示，由于相对的两个区域属于同一方向，所以8个区域实际属于4个方向，8个区域的悬垂系数计算如公式（1）所示：

式中：S投影为各区域的投影面积；S圆盘为各区域的圆盘面积；S试样为各区域试样的投影前面积。最后将属于同一方向的两个区域的悬垂系数取平均，即为该方向的悬垂系数，即求出织物0°、90°、45°和135°的悬垂系数。

d）织物悬垂各向差异指标：经纬最大展宽之比和斜向最大展宽之比。经纬最大展宽之比A1的计算方式为试样经向与纬向最大展宽的比值；斜向最大展宽之比A2的计算方式为试样45°与135°方向最大展宽的比值。

1.4 织物弯曲性测试

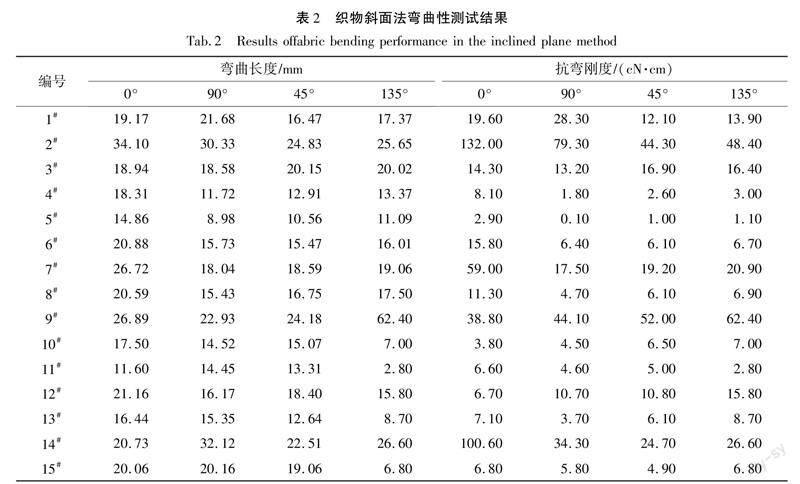
由于伞式测量法本身无法得到某一具体方向的性能，而弯曲性和悬垂性都是表示织物柔软程度的性能，因此选取可测某一具体方向性能的弯曲性作为悬垂性的比较标准。根据GB/T 18318.1—2009《纺织品 弯曲性能的测定 第1部分：斜面法》，用YG（B） 022D型全自动织物硬挺仪（温州大荣纺织仪器有限公司），测试表1中15块试样0°、90°、45°和135°的弯曲长度和抗弯刚度。

2 结果与讨论

织物斜面法弯曲性测试结果见表2，新指标的测试结果见表3，其中弯曲长度、抗彎刚度和3项新指标均是织物4个方向测试结果的平均值，且每个方向均为正反面共10个测试结果的平均值。

2.1 新指标与弯曲长度和抗弯刚度的相关性

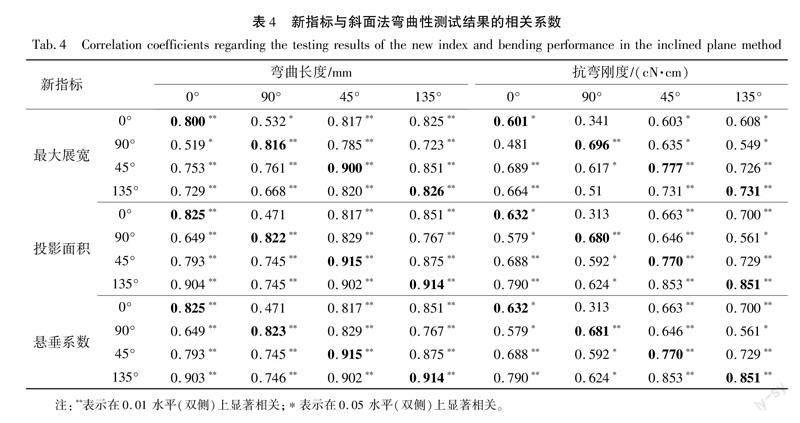
为探究悬垂性新指标与弯曲性是否具有良好的相关性，将15块试样4个方向的新指标分别与弯曲长度和抗弯刚度进行相关分析，新指标与弯曲性测试结果的相关系数如表4所示。

表4显示，4个方向的最大展宽、投影面积和悬垂系数与弯曲长度和抗弯刚度均具有较高的相关性，在0.01的显著性水平上高度相关，具体来看，新指标与弯曲长度的相关性好于抗弯刚度，对新指标分别与弯曲长度进行回归分析，得出新指标与弯曲长度回归的R2值分别是0.65、0.71、0.70，因此后面重点分析投影面积和悬垂系数与弯曲长度的关系。新指标与抗弯刚度的相关性较弱，是因为织物的抗弯刚度计算时还需考虑织物克重，而本文中的新指标均未包含织物克重。

表4可以看出3个新指标与弯曲长度和抗弯刚度均呈正相关关系。说明织物越硬挺的方向（即弯曲长度和抗弯刚度越大），用伞试测量法测得该方向的最大展宽、投影面积、悬垂系数也越大。

从表4还可以看出，4个方向的投影面积和悬垂系数与弯曲长度的相关系数几乎一样（除90°略有差异外），均高于最大展宽与弯曲长度的相关系数。这是因为悬垂系数是利用投影面积计算得到的，因而其相关性高于最大展宽。

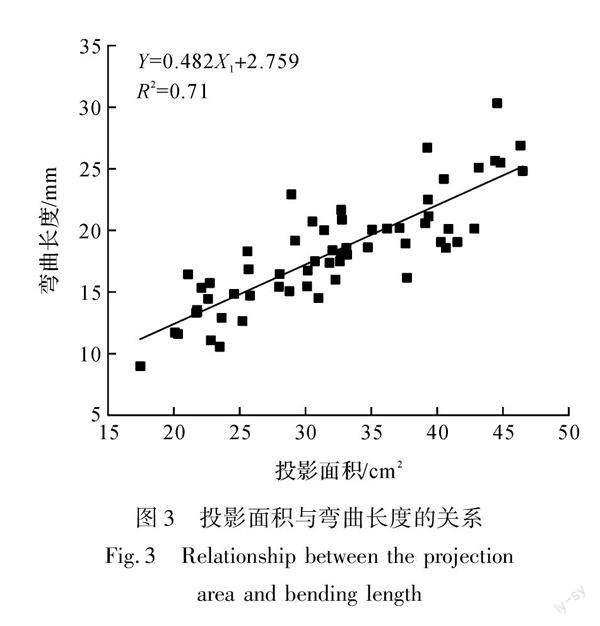
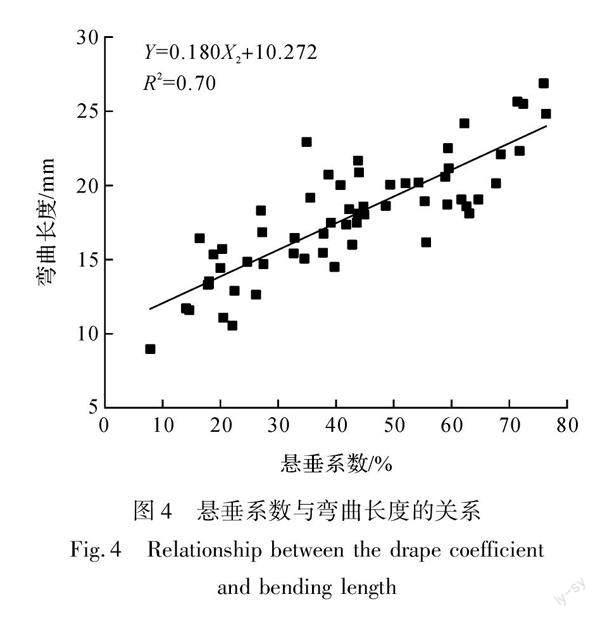
图3与图4分别示出了投影面积和悬垂系数与弯曲长度的关系，图中的样本量为60个（15块织物，每块织物4个方向）。

从图3可以看出，投影面积与弯曲长度呈正相关关系，其具体关系式为：Y=0.482X1+2.759，R2=0.71，其中：Y表示弯曲长度，mm；X1表示投影面积，cm 说明伞式测量法所测投影面积越大的织物，其斜面法所测的弯曲长度也越大。

从图4可以看出，悬垂系数和弯曲长度也呈正相关关系，其具体关系式为：Y=0.180X2+10.272，R2=0.70，其中：Y是弯曲长度，mm；X2是悬垂系数，%，即悬垂系数越大的织物，其弯曲长度也越大。究其原因，越硬挺的织物，其悬垂性越差，抵抗弯曲变形的能力越大，越不易弯曲。由此可知，测试悬垂性的伞式測量法和测试弯曲性的斜面法所测结果具有较好的相关性，且伞式测量法所测的投影面积越大，则斜面法所测弯曲长度也越大（即越硬挺），越不易弯曲变形。

由图3和图4可知，投影面积和悬垂系数与弯曲长度的相关性较好，但图中的点并没集中在拟合线周围。这是因为悬垂试样为圆形，各个方向的分界并不明显，其自然悬垂形态受织物面料各向性能的影响。此外，悬垂性除了与织物弯曲性有关外，还与织物剪切性有关，而本文比较的仅为弯曲性与悬垂性的关系。因此二者的相关系数没有特别高。

2.2 基于伞式测量法的织物悬垂各向差异分析

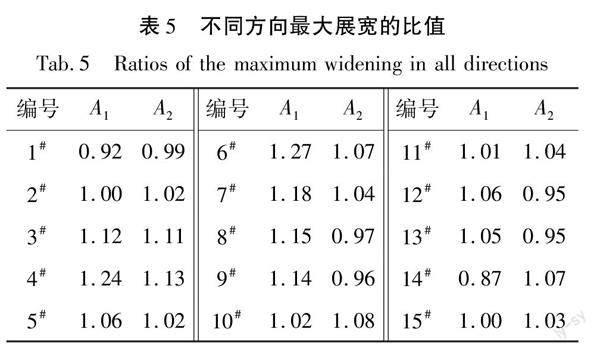
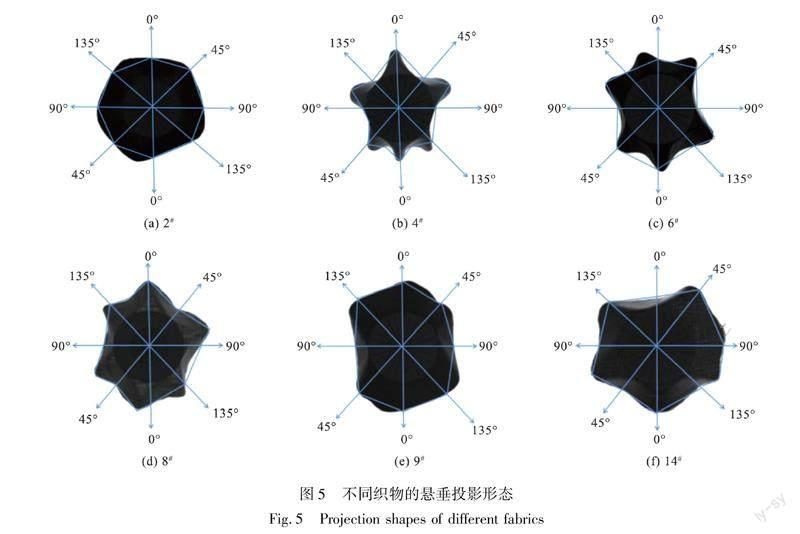
为分析织物不同方向的悬垂性差异，计算经纬最大展宽之比A1和斜向最大展宽之比A2，不同方向最大展宽的比值如表5所示，图5示出了不同织物的悬垂投影形态。

从表5中可看出，织物的经纬向与斜向均有差异，有的差异明显，有的差异不明显，结合图5可知：2#各方向都很硬挺，经纬及斜向最大展宽之比差距较小，即各向差异不明显；4#经纬向最大展宽之比大于斜向，经纬向均硬挺，易形成波峰，而斜向较柔软，易形成波谷，各向差异较明显；6#经纬最大展宽之比较高，且经向较硬挺，纬向较柔软，而135°和45°的斜向差异较小，均较硬挺；8#经纬向和135°方向较硬挺，45°方向较柔软，各向差异较明显；9#纬向较柔软，其他方向较硬挺，经纬向差异比斜向大；14#经向较柔软，纬向斜向较硬挺。其中2#、4#、8#和14#均为平纹织物，对于硬挺的平纹织物，其各向差异不明显，而对于柔软的平纹织物，其纬向悬垂性可能比经向好，135°比45°的悬垂性差。6#、9#为斜纹织物，其斜向悬垂性比经纬向好。由此可知，伞式测量法所得织物的投影形态经过方向标记及指标提取，可以用来表征织物悬垂性的各向差异。

综上，织物的悬垂性与弯曲性之间存在相关关系，织物某方向的悬垂性越差，抵抗弯曲变形的能力就越大，织物也就越不易弯曲，即伞式测量法所测悬垂性结果与斜面法所测弯曲性结果之间具有较好的相关性，因此改进后的伞式测量法所得的织物悬垂投影形态可以用来判断织物的各向差异。

3 结 论

针对传统伞式测量法只能测试织物整体悬垂性的不足，本文对其进行改进，通过方向标记的方法，对织物0°、90°、45°和135° 4个方向悬垂性的差异进行研究，并根据悬垂图像提取了3个新的评价指标，研究结果表明：

a）0°、90°、45°和135° 4个方向的最大展宽、投影面积和悬垂系数与弯曲长度和抗弯刚度均具有较好的正相关关系，且与弯曲长度的相关性高于抗弯刚度，说明本文的改进方法具有良好的可行性。

b）本文结合织物的弯曲性进行研究，发现织物的悬垂性和弯曲性存在相关关系，织物某方向的悬垂性越差，其抵抗弯曲的能力就越大，则该方向越不易弯曲。

c）利用改进的伞式测量法所得的织物悬垂投影形态可以判断织物悬垂性和弯曲性的各向差异，织物硬挺的方向易形成波峰，柔软的方向易形成波谷，使设计师对织物各向差异性一目了然，更利于服装设计时的选材。

参考文献：

［1］周玲玲，齐红衢，周华.织物悬垂形态测试及其评价指标的研究［J］.现代纺织技术，2010，18（3）：46-50.

ZHOU Lingling， QI Hongqu， ZHOU Hua. Research on fabric draping shape test system and its evaluate parameters［J］. Advanced Textile Technology， 2010， 18（3）： 46-50.

［2］王霞，罗戎蕾.织物悬垂性的研究现状及发展趋势［J］.纺织导报，2021（9）：78-82.

WANG Xia， LUO Ronglei. Research status and development trends of fabric drapability［J］. China Textile Leader， 2021（9）：78-82.

［3］张晓婷，洪剑寒，査神爱，等.基于三维扫描技术的毛织物悬垂性能测试方法［J］.毛纺科技，2015，43（10）：58-61.

ZHANG Xiaoting， HONG Jianhan， ZHA Shenai， et al. Study on the drape performance testing method of wool fabric with three-dimensional scanner［J］. Wool textile Journal， 2015， 43（10）： 58-61.

［4］RYKLIN Dzmitry，汤晓彤.评估织物悬垂性的新方法［J］.现代纺织技术，2022，30（1）：109-114.

RYKLIN Dzmitry， TANG Xiaotong. Development of a new method for evaluating the drapability of fabrics［J］.Advanced Textile Technology， 2022， 30（1）：109-114.

［5］余芳，刘成霞，尹清一.倒Ω法测试织物弯曲性及悬垂性［J］.丝绸，2019，56（2）：27-31.

YU Fang， LIU Chengxia， YIN Qingyi. Measurement of fabric bending and draping performance with inverse Ω method［J］. Journal of Silk， 2019， 56（2）： 27-31.

［6］韩燕娜.织物弯曲性与悬垂性测试新方法［J］.丝绸，2019，56（4）：30-34.

HAN Yanna.A new testing method for fabric bending ＆ draping behavior［J］. Journal of Silk， 2019， 56（4）： 30-34.

［7］李强，过玉清，纪峰.基于仰视投影的织物悬性测试方法［J］.纺织学报，2008，29（3）：34-37.

LI Qiang，GUO Yuqing， JI Feng.Testing method of fabric drape based on upward projection［J］. Journal of Textile Research， 2008， 29（3）： 34-37.

［8］敬凌霄，张才前，汪涛，等.图像法测试织物悬垂性能的各向差异［J］.纺织学报，2010，31（8）：32-35.

JING Lingxiao， ZHANG Caiqian，WANG Tao， et al. Evaluation on difference between fabric warp wise and weft wise draping properties by imaging technology［J］. Journal of Textile Research， 2010， 31（8）： 32-35.

［9］BRUNIAUX P， GHITH A， VASSEUR C.Modeling and parametric study of a fabric drape［J］. Advances in Complex Systems， 2003，6（4）：457-476.

［10］黃新林，李汝勤.织物悬垂性图像测试方法［J］.纺织学报，2006，27（11）：14-19.

HUANG Xinlin， LI Ruqin. Image test method for fabric drape［J］. Journal of Textile Research， 2006， 27（11）： 14-19.

Research onfabric draping anisotropy

SONG Weinaa， LIU Chengxiaa，b

Abstract： The draping of fabrics is mostly tested without distinguishing between directions， angenerally， the overall draping is researched. However， the same fabric has significant differences in draping due to different warp and weft yarn densities or distinct fabric structures. Therefore， researching the draping of different directions is necessary. To study the differences of fabric drape performance at different directions， the traditional method of umbrella-shaped measurement was improved in this study. First， 15 common fabrics were chosen， XDP-1 fabric drape tester was used to test the draping performance in the four directions of 0°， 90°， 45°， and 135°， and drape images were obtained. Based on the obtained images， new indexes were extracted： the maximum width， projected area and drape coefficient， and the relationship between fabric drape indexes in all directions and bending length and bending stiffness was analyzed.

The maximum widening L， projected area S and drape coefficient D are compared with the bending length and bending stiffness in the four directions. Results show that the new indicators have high correlation with both the bending length and bending stiffness， with a high correlation at a significance level of 0.01， and the three new indicators are positively correlated with the bending length and bending stiffness. The harder the fabric， the greater its maximum widening and projection area. In other words， the poorer the drape of the fabric， the less prone it is to bending， and the greater its ability to resist bending deformation. The equation between the projected area and bending length is a linear function： Y=0.482X1+2.759， R2=0.71， where Y represents the bending length （mm） and X1 represents the projected area （cm2）. And the equation between the drape coefficient and bending length is a cubic function： Y=0.180X2+10.272， R2=0.70， where Y is the bending length （mm） and X2 is the drape coefficient （%）. Then， based on the umbrella method， the anisotropy of fabric drape is analyzed and two indicators are extracted： the maximum widening ratio A1 of warp and weft and the maximum widening ratio A2 of oblique direction. Anisotropy analysis is conducted by combining the drape projection shapes of different fabrics.

The results show that all three new indicators have good correlation with bending length and bending stiffness. The direction of fabric stiffness is prone to wave peaks， while the direction of softness is prone to wave valleys. The better the drape of the fabric in a certain direction， the easier it is to bend， and the smaller the bending resistance in that direction. Therefore， the drape projection of a circular sample can be used to estimate the bending performance of the fabric in a certain direction. It is feasible to measure the drape anisotropy of the fabric by using the umbrella method.

Keywords： fabric; drape coefficient; maximum widening; projected area; fabric drape; bending property

收稿日期：20230506 网络出版日期：20230807

基金项目：浙江省自然科学基金项目（LY20E050017）；国家自然科学基金项目（51405446）

作者简介：宋委娜（1999—），女，山东济宁人，硕士研究生，主要从事服装数字化方面的研究。

通信作者：刘成霞，E-mail： glorior_liu@163.com