串并有向图的判定算法及应用实例

王琪

(江西制造职业技术学院 江西 南昌 330095)

单机排序问题已经有大量的研究，何欣怡[1]研究了带拒绝的若干单机排序问题，包括工件带有截止日期约束、带有退化和不可用区间和机器有不可用区间且工件不可恢复等相关子问题。种贝贝[2]针对两个代理所考虑的3 个不同目标函数组合，分别讨论了它们的KS 公平定价问题。栗苹[3]研究总提前损失问题，包括工件将根据其工期前完成部分工件的持续时间进行处罚。其他相关研究进展包括基于凸优化方法[4]、基于工件排列顺序与公共窗口的位置优化的方法[5]、基于划分接受工件集和拒绝工件的方法[6]。此外，作为该问题的重要解决思路，串并有向图经常作为约束条件使用，其应用范围十分广泛。例如：成龙等人[7]提出的关于1｜sp_Graph｜∑Wj(1-e-rcj)问题的最优算法；闫杨等人[8]研究的1｜sp_Graph｜WjCj问题；高文军等人[9]讨论工件间具有串并有向图约束的preempt-repeat 模型，则是用LAWLER EL[10]提出的任务合并和由底向上搜索分解树的方法求解；陈昊[11]、张大宇[12]、黄玉[13]、万龙[14]这些学者在相关研究中也均涉及串并有向图。这些问题中工件间的优先约束均为串并有向图，但是串并有向图仅仅是作为既定的前提约束条件，并没有对这个约束条件进行判定。而据笔者所知，在现有研究中，只给出了串并有向图的定义或者其分解树的特征，根据这些定义或者特征只能提取出串并有向图的必要条件，均不能成为判断一个有向图是否为串并有向图的充分条件。所以，研究串并有向图的判定算法问题具有重要意义。

1 相关定义

为了解决串并有向图的判定问题，首先需要明确与串并有向图相关的定义。相关定义如下文所述。

定义1[15]一个有向图G是一个有序二元组，记为G=(N，A)，其中N={}n1，n2，…nn称为G的点集合，A={aij}称为G的弧集合，aij是一个有序二元数组(ni，nj)，记为aij=(ni，nj)，称aij从ni连向nj，ni称为nj的前继，nj称为ni的后继。

定义2[15]对有向图G的每条弧如果均用一条边代替它，得到一个无向图，这个无向图称为G的基本图。

定义3 某个点前继的数量表示该点的入度，后继的数量表示为该点的出度，删除某个点包括删除该点和与该点相连的边。

定义4[15]两个端点重合为一点的边称为环，两个端点都相同的边称为重边，一个有向图，如果它既没有环，也没有重边，则称为简单有向图。

定义5[15]在有向图G中，一个点和弧的交错序列(ni，aij，nj，…n1)称为G中由ni到n1的一条有向路，记为(ni，n1)有向路。G中一条至少包含一条弧，并且ni=n1的(ni，n1)有向路，称为G的一条有向回路。

定义6[15]对有向图G，定义一个n×n阶的邻接矩阵A=(aij)，其中A称为G的邻接矩阵。

图的表示方法很多，采用不同的表示方法，可获得图的不同的时空性能[16]。用邻接矩阵表示图的优点是易于计算机存储。

定义7[15]图G中若存在一条由ni到nj的路。则称ni和nj是连通的，如果G中任意两点都是连通的，则称G是连通的。设N'⊆N，E′⊆E，如果对E′中任意一条边eij={ni，nj}，都有ni∈N′和nj∈N′，则称G′=(N′，E′)是G的一个子图。G的极大连通子图称为G的一个连通分支。

本文中定义的有向图的连通，指的是如果其基本图是连通的，则表示该串并有向图连通，串并有向图中的连通分支对应其基本图相同点和边的连通分支。

定义8[10]可迁的串并有向图按如下递归方式定义。

（1）仅包含一个顶点的有向图是可迁的串并有向图。

（2）若G1=(N1，A1)和G2=()N2，A2是可迁的串并有向图，且N1∩N2=∅，则G=G1×G2=(N1∪N2，A1∪A2∪N1×N2)是可迁的串并有向图，称G是由G1和G2串行合成的。

（3）若G1=(N1，A1)和G2=(N2，A2)是可迁的串并有向图，且N1∩N2=∅，则G=G1×G2=(N1∪N2，A1∪A2)是可迁的串并有向图，称G是由G1和G2并行合成的。

（4）通过有限步应用（1）（2）（3）得到的有向图是可迁的串并有向图。

串并有向图的主要特征是在一个串并有向图中，所有结点均为串行或并行关系。串行关系的结点有先后顺序，并行关系的结点为平行关系，没有先后顺序。通过串并有向图的定义可知在串并有向图中不存在回路。

定义9[15]一个树是一个连通且无回路的图。

定义10 二叉树的递归定义。

二叉树(Binary Tree)是n(n≥0)个结点的有限集，它或者是空集（n=0），或者由一个根结点及两棵互不相交的、分别称作这个根的左子树和右子树的二叉树组成。

树是图的特例。一个串并有向图G可以分解为一个二叉树Tr，Tr 称为图G的分解树。如图1 所示，图1（a）表示一个串并有向图，图1（b）表示其对应的分解树。Tr的叶子结点对应G的顶点，中间结点用S或P表示。S表示其左右两个子树之间是串行关系，并且左子树优先于右子树，P表示左右两个子树之间是并行关系。

图1 一个串并有向图及其分解树

本文提出的串并有向图的判定算法，其主要思想是对一个给定的有向图的所有连通分支逐一进行递归分解，若所有连通分支都满足相关条件，则判定该有向图是串并有向图。通过该算法能够准确判断一个有向图是否为串并有向图。

2 算法描述

串并有向图判定算法的主要过程：令G1,G2,…,Gn是有向图G（非空图）的n个连通分支。对Gi(i∈1，…，n)，找到其所有入度为0 的结点，定义为结点集K，如果K为空集，则说明Gi中包含有向回路，判定Gi不是串并有向图，如果K不是空集，删除K中的所有结点后再找到新的有向图中所有入度为0 的结点，定义为结点集T。如果T为空集，则说明Gi为单节点，根据定义8 的（1）说明Gi是串并有向图，如果T不为空集，则判断图G中是否使结点集K中每一个点ni与结点集T中的任意一点ni都存在由ni指向nj的有向弧相连。如果否，则Gi中不是串并有向图，如果是，则在Gi中中删去点集K定义为新的图Gi中，重复以上过程，进行递归判断。若G1,G2,…,Gn均是串并有向图，则最终判定图G为串并有向图。

Aa是G的连通分支Ga的n×n阶邻接矩阵，对图G，运行以下算法H。

步骤1：DefineG1.G2…Gp⊆G；

步骤2：func(Gq)｛Tq=1；

步骤4：IfK≠∅ ThenTq=0；

步骤5：ElseGq′:=Gq-K；

步骤7：IfT≠∅ Then

步骤9：If func(Gq) =0 ThenTq=0 End End End End

步骤10：ReturnTa；｝

步骤11：tg=1；

步骤12：for ｛q=1;q≤p;q++｝

步骤13：｛If func(Gq)=0 Then tg=0 and Break；End｝

步骤14：If tg=1 then ReturnGis sp-Graph

步骤15：Else ReturnGis not sp-Graph End

3 算法的证明

定理1 算法H解决了串并有向图判定的问题。

证明 对于任意有向图G=(N,A)的任意一个连通分支Ga，Ga的分解树为Ta，假设{n1，n2，…，nk}表Ga中入度为0 的点集K，若K=∅，则说明Ga中存在有向回路，判定Ga不是串并有向图；若K≠∅，｛nk+1…nt｝表示Ga删去K中的点之后新的入度为0的点集T，若T=∅，则说明Ga是单节点，判定Ga是串并有向图，若T≠∅，则在Ga中，只有ni(ni∈K)入度均为0，表明ni(ni∈K)的优先顺序在Ga的点集Na中是最高级，所以在Ta中，对任意一结点nj(nj∈T)，ni(ni∈K)一定都是nj的祖先结点。找到离nj最近的S结点，设为S′。则n1…nk在S′的左子树中，nk+1…nt在S′的右子树中，表明K中的结点优先于T中的结点。因为n1…nk之间没有优先顺序，所以它们之间为并联关系，通过P结点相连，说明S'的左子树中除了叶子结点之外全为P节点。同理，对于T中的结点也均为并联关系，S′的右子树中除了叶子结点之外全为P节点。所以在Ta中由ni(ni∈K)到nj(nj∈T)的路径上只有一个S′结点，其余均为P结点。对应于原图Ga，则说明ni与nj之间为串联关系，ni与nj之间存在有向弧由ni指向nj。所以K中和T中的所有点相互之间均为串联或并联关系。令Ga删去K，重复以上分析过程，证明Ga中所有点均为串并关系，Ga是串并有向图。若G的所有连通分支都是串并有向图，肯定能判定G是串并有向图。

4 算法的实践

对于串并有向图2（a），其连通分支即为其本身。图2（a）中入度为0 的点为n1，定义K={n1}，删去K后得到图2（b），图2（b）中入度为0的结点包括n2和n3，定义T=｛n2,n3｝，由算法的证明可知，n1的优先级高于n2，n2与n3的优先级相同，假设在图2（a）的分解树中，S1是离n2最近的S结点，所以n1在S的左子树中，n2、n3在S1的右子树中并且n2、n3通过P结点相连，得到分解树图2（c），再在图2（b）中删去T，得到图2（d），图2（d）中n4入度为0，则n2与n3均为n4的祖先结点，n4与n2、n3串联，则n4在离n4最近的S结点S1的右子树中，n2、n3在S1的左子树中，所以在图2（c）的基础上加上n4后得到图2（e）；图2（d）删去n4后得到图2（f），图2（f）中n5、n6是入度为0 的结点，则n4是n5、n6的祖先结点，并且n5和n6并联，n4在离n5最近的S结点S2的左子树中，n5和n6在S2的右子树中，所以在图2（e）的基础上得到图2（g）。图2（g）是一个分解树，这说明根据算法的证明过程进行分解后，图2（a）的确为一个串并有向图。

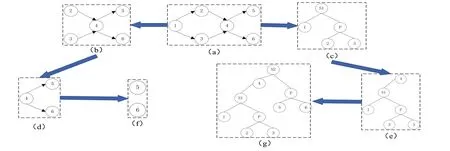
图2 一个串并有向图的应用实例

对于有向图3（a），其连通分支有且仅有一个，即为其本身。图3（a）中入度为0 的点为n1、n3，删去n1n3后得到图3（b），图3（b）中入度为0 的结点为n2、n4，则在图3（a）的分解树中，n1n3为并联关系，n2n4也为并联关系，并且n1、n3为n2n4的祖先结点，得到分解树图3（c），但是由图3（c）可知n1优先于n4，在图3（a）中n1n4并不存在优先约束关系，所以图3（c）并不是图3（a）的分解树，图3（a）没有对应的分解树，所以图3（a）并不是串并有向图。

图3 一个非串并有向图的应用实例

通过图2和图3两个例图可以发现，如果一个有向图G是串并有向图，则通过算法H的证明过程可以将G分解为一个对应的分解树，验证其为串并有向图；如果一个有向图G不是串并有向图，通过算法H，G不能分解成一个分解树，验证其不是串并有向图。

5 结语

本文首先定义相关概念，其次描述串并有向图的判定算法的主体思想，进而提出算法H，通过证明发现算法H适用于判定有向图是否为串并有向图的问题，最后通过实例证明算法H能够解决相关问题。