广义乘子法求解构造变分问题的神经网络方法

欧阳晔，江 巍，吴 怡，冯 强，郑 宏,3

(1.三峡库区地质灾害教育部重点实验室，湖北，宜昌 443002；2.三峡大学土木与建筑学院，湖北，宜昌 443002；3.北京工业大学建筑工程学院，北京 100124)

在工程领域，力学问题的数学模型往往都是以微分方程的形式提出的，微分方程与初边值条件一起构成了微分方程的定解问题[1]。求解偏微分方程的途径可分为解析法与数值解法两大类。解析法适用于形状规则的简单问题，以逆解法、半逆解法为代表。实际问题的边界条件往往比较复杂，解析法求解困难，于是发展出了以有限差分法、有限单元法等为代表的数值解法，这些算法的求解效果严重依赖事先剖分的网格。此外，有限差分法在不同的方程上需使用不同的差分格式；有限单元法针对不同的问题需选取不同的单元类型，这些局限性大大影响了其应用范围[2]。

神经网络算法的飞速发展[3]和Tensorflow[4]、Pytorch[4-5]等深度神经网络框架的发布，使得近年来神经网络的应用研究呈现井喷式发展，如叶继红和杨振宇[6]采用生成式对抗神经网络生成的风场数据与目标数据之间具有相同的特性；许泽坤和陈隽[7]利用神经网络准确预测了地震作用下框架结构的非线性结构响应；程诗焱等[8]基于BP 神经网络提出的地震易损性曲面分析方法，利用该方法可以得到可信的损伤概率结果；赵林鑫等[9]将比例边界有限元法与神经网络相结合，建立适用于薄板结构裂纹状缺陷识别的反演模型；郑秋怡等[10]建立了基于长短时记忆神经网络的大跨拱桥温度-位移相关模型，可准确描述多元温度与位移的非线性映射关系。为克服传统数值解法求解偏微分方程时的局限性，国内外学者尝试将神经网络引入偏微分方程的求解，深度Ritz 法[11]、深度伽辽金法[12]、深度能量法[13]等相继被提出，并取得了初步成功应用。RAISSI 等[14-15]提出的物理信息神经网络(Physics Informed Neural Networks,PINN)，将原问题的物理信息嵌入到神经网络中，通过训练神经网络获得近似解；LU 等[16]提出了一种改善PINN训练效率的自适应细化算法，并开发了DeepXDE 求解器；郭宏伟和庄晓莹[17]提出了一种使用Adam 与LBFGS 两种优化器训练神经网络的策略，克服了传统神经网络训练的结果易陷入局部最优解的问题；黄钟民等[18]发展了一种耦合神经网络方法用于求解面内变刚度薄板的位移与挠度；唐明健和唐和生[19]使用神经网络求解了矩形薄板的力学正反问题；HE 等[20]从逼近论的角度证明了使用ReLU 激活函数的神经网络与有限元是等价的。

上述研究中，边界条件的施加与传统有限元略有不同。现有研究中神经网络的损失函数是一个包含控制方程与边界条件的泛函，通常使用经典罚函数法进行构造，将原约束优化问题转化为无约束优化问题，如郭宏伟等[17]、黄钟民等[18,21]。理论上罚函数法中罚因子的数值应为一个无穷大的数[22]，在实际计算中，罚因子取得过大会造成方程的病态导致无法求解，取得过小则无法起到惩罚的作用，其值不易把控。以L1精确罚函数法[23]为代表的改进方法，可有效克服经典罚函数法中罚因子需趋近于无穷的局限，并在非线性规划问题的神经网络求解中取得成功应用[24-25]，罚因子的具体取值仍依赖于人为确定。

Lagrange 乘子法[26]也可将约束优化问题转化为无约束优化问题，但采用Lagrange 乘子法构建的神经网络同样存在一定不足。当神经网络损失函数对应的Lagrange 函数在平衡点处其Hessian 矩阵为非正定矩阵时，该平衡点将偏离原问题的最优解[24]。理论上，广义乘子法可克服Lagrange 乘子法的这一局限[22]。鉴于此，针对边界条件复杂的偏微分方程组，本文提出一种采用广义乘子法施加边界条件的神经网络方法。该方法首先通过神经网络获得预测解，再使用广义乘子法构建损失函数并计算损失值，最后利用梯度下降法进行参数寻优，判断损失值是否满足要求；若不满足，则更新罚因子与乘子后再进行求解，直至损失满足要求。为验证新方法的求解精度和计算效率，本文求解了Kirchhoff 薄板和简支梁问题，并与使用经典罚函数法、L1精确罚函数法、Lagrange乘子法施加边界条件的神经网络求解进行比较。此外，采用不同拓扑结构的神经网络和域内配点求解Kirchhoff 薄板问题，探讨了神经网络拓扑结构与域内配点数对新方法求解精度的影响。

1 微分方程及其泛函

工程技术领域，许多自然规律是以偏微分方程(组)的形式提出的，常见的偏微分方程分为三大类：椭圆型方程、抛物型方程、双曲型方程，上述方程的共同点在于方程内部包含待求解的未知场量及其导数，即：

式中：A为偏微分方程组；u为物理量；Ω 为问题求解区域。静态场问题边值条件通常分为三类：第一类条件为指定未知场量在边界上的值；第二类条件为指定未知场量在边界外法线方向上的值；第三类条件为上述两类边界条件的线性组合，即：

式中：B为边界条件组；Γ 为求解区域的边界。

式(1)所示的控制方程与式(2)所示的边值条件一起构成了微分方程的定解问题。通常来说，微分方程对解的要求较高，若直接对微分方程进行求解较为困难，因此常使用加权余量法获得微分方程的等效积分弱形式，弱形式会降低对解的要求。对满足线性、自伴随的微分方程而言，采用伽辽金加权余量法所获得的等效积分弱形式与使用自然变分原理获得的泛函是相同的，弱形式将具备明确的物理意义，例如，弹性力学中平衡微分方程的等效积分弱形式就是虚功方程。对不满足线性、自伴随的微分方程而言，需使用构造变分原理来获得泛函，使用罚函数法构造的泛函表达式如下：

式中：v为一组与A(u)方程个数相同的任意函数；M为罚因子，是一个标量。

2 神经网络方法

2.1 神经网络基本原理

神经网络是一个由权重w、偏置b、激活函数σ 等定义的非线性函数，神经网络的输入x，输出为u(x)，其前向传播可表达为：

式中，下标l表示神经网络的层数，Fl(l=1, 2, 3, … ,l)为第l层的映射规则，定义为：

初始状态下，神经网络中参数θ={w;b}是随机生成的，不能满足实际要求，需进行参数更新，现阶段常使用BP 算法进行参数更新。

万能近似定理[20]指出，神经网络具有逼近任意复杂非线性函数的能力。神经网络具有强大非线性函数拟合能力的关键在于其激活函数是非线性的。现有研究中常使用ReLU 函数和Tanh 函数两种激活函数。ReLU 函数[27]的表达式为：

该函数及其导数图形如图1(a)和图1(c)所示。ReLU 函数形式简单、计算成本低，可避免出现梯度消失现象。Tanh 函数具有C∞性质，其表达式为：

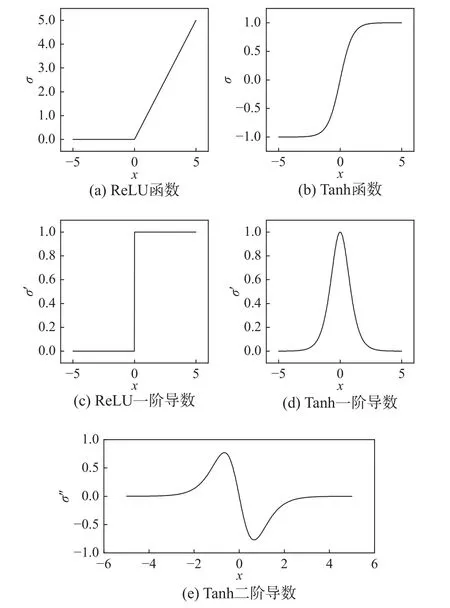
图1 两种常用的神经网络激活函数及其导数Fig.1 Two widely used activation function in neural network and their derivatives

当式(3)涉及未知场量的高阶导数时，Tanh函数更为适用，因此在目前神经网络求解力学问题中广泛使用[17-18]，该函数及其导数图形如图1(b)、图1(d)和图1(e)所示，本文采用Tanh 函数为激活函数。

2.2 深度配点法

深度配点法是由RAISSI 等[14-15]提出的一种由物理信息驱动的神经网络模型。根据万能近似定理，偏微分方程组的解u可使用神经网络来逼近。对于深度配点法，需首先在求解域内布置一系列的散点xΩ，另外边界上也需布置一系列的散点xΓ。图2 给出了一矩形区域的配点示意，点★代表xΩ，点●代表xΓ，散点x={xΩ;xΓ}构成了神经网络的训练数据。

图2 配点示意图Fig.2 Schematic diagram of collocation points

从偏微分方程出发构建如图3 所示的物理信息网络。左边的神经网络作为偏微分方程的近似解，输入为散点坐标，输出 ^u(x;θ)由式(4)计算。右边的物理信息则是将近似解^u带入控制方程与边界条件中所产生的余量。

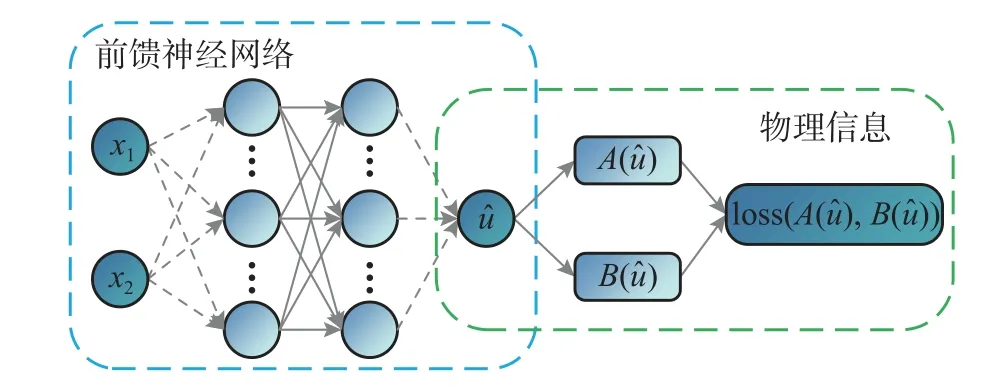
图3 物理信息网络示意图Fig.3 Diagram of Physics Informed Neutral Network

深度配点法一般采用经典罚函数法施加边界条件，建立的神经网络损失函数表达式为：

式中：NA、NB分别为微分方程与边界条件方程的个数；PΩ、PΓi分别为域内、相应边界上的配点数；M为罚因子；其中A(x;θ)与B(x;θ)共享同一套超参数θ，并且都是坐标的函数。当loss 取得最小值时，^u(x;θ)就是偏微分方程的近似解。

将经典罚函数法替换为L1精确罚函数法，则神经网络损失函数的表达式变化为：

式中，|·|为绝对值。

如果使用Lagrange 乘子法施加边界条件，建立的神经网络损失函数为：

式中，ki为Lagrange 乘子。

2.3 采用广义乘子法施加边界条件的深度配点法

如引言中所述，使用经典罚函数法、L1精确罚函数法、Lagrange 乘子法施加边界条件的神经网络在求解时均存在一定的局限性。广义乘子法[20]结合了罚函数与Lagrange 乘子法的优点，使得罚因子在适当大的情况下也能求得原约束问题的解。因此，本文将广义乘子法引入神经网络之中，提出一种基于广义乘子法施加边界条件的神经网络方法。该方法左边的神经网络仍由式(4)计算，右边的物理信息则基于广义乘子法构建，最终建立的神经网络损失函数表达式为：

式中：M为罚因子；ki为相应边界方程对应的乘子，当loss 取得最小值时，^u(x;θ)就是偏微分方程的近似解。使用梯度下降法训练参数θ，从而使得loss 取得最小值，具体做法如下：

S1 在求解域内与边界上布置一系列的配点；

S2 利用广义Lagrange 乘子法将约束问题转化无约束的待优化函数，得到式(11)；

S3 构建前馈神经网络，并将其作为试函数；

S4 给定初始值θ0，初始乘子初始罚因子M0，放大系数α>1，误差阈值ε，参数γ∈(0,1)。这里，各量的上标代表迭代次数；

S5 问题求解：以θn-1为起始点，利用梯度下降法求解当前乘子、罚因子下的最优解θn，具体做法为：

① 计算损失函数loss 的值，判断损失函数的值是否达到精度要求；若达到要求，则进入S6，若未达到要求，则进入②。

② 将损失标量loss 对神经网络参数θ 求偏导，并更新神经网络参数，其更新公式为：

式中：Δθn-1为θn-1的更新量；η 为神经网络学习率。参数更新完毕后进入①。

S6 判断迭代终止条件：根据下式计算边界上的误差h(θn)，若h(θn)<ε 成立，则停止迭代并输出θn；否则，进入步骤S7；

否则：

S8 更新乘子项：使用如下公式更新乘子项及迭代次数，并返回步骤S5：

3 算例分析

本文求解程序均采用Python 的Tensorflow2.6版本进行编写，运行平台为Windows10，硬件配置为CPU：Intel Xeon E-2224 @ 3.40 GHz，GPU：NIVIDIA Quadro RTX 4000。

3.1 周边简支矩形Kirchhoff 薄板

如图4 所示的周边简支矩形Kirchhoff 薄板，边长a=b=1 m，薄板厚度h=0.01 m，弹性模量E=10 MPa，泊松比ν=0.2，板中面的均布荷载为q=10 N/m2，该问题的重三角级数解[28]为：

图4 Kirchhoff 矩形薄板示意图Fig.4 Diagram of a Kirchhoff thin rectangular plate

该问题的微分控制方程为：

其边界条件为：

式中：Γ={Γ1，Γ2，Γ3，Γ4}为边界，分别代表{x=0，x=a，y=0，y=a}四条边；Mn为弯矩。

根据广义乘子法构建的损失函数为：

式中：PΩ、PΓi分别为域内、相应边界上的配点数；ki为相应边界方程对应的乘子。

初始设定罚因子M=1，乘子ki=1(i=1, 2, …, 8)，放大系数α=2，误差阈值ε=1×10-3，参数γ=0.01，采用本文提出方法进行求解。按照图2 的方式在求解域与边界上进行配点，其中域内配点20×20 个，边界上每边配点40 个。神经网络的拓扑结构设置为2-1*30-1，表示输入层神经元数量为2，分别为配点的横纵坐标；隐藏层层数为1，隐藏层神经元数量设置为30 个；输出层神经元数量为1，为配点的挠度预测解，优化器选取Adam，学习率设置为0.01。在神经网络训练过程中，若损失值连续500 轮没下降则自动更新罚因子、乘子后再进行计算，且在每轮罚因子、乘子下的训练不超过10000 轮。

经典罚函数法、L1精确罚函数法、Lagrange乘子法施加边界条件建立的神经网络求解该算例时，配点方式、神经网络拓扑结构、激活函数、优化器和学习率等设定均与本文算法求解时的设定保持一致，训练完毕后取损失值最小的一轮作为输出结果。为探讨罚因子取值对结果的影响，经典罚函数法和L1精确罚函数法的罚因子分别取M=1、10、50、100、500 和1000。Lagrange 乘子法的乘子初始值设定与本文算法求解时的设定相同。

以配点处的神经网络预测解与重三角级数解[28]的绝对误差平均值作为参考，对上述神经网络求解结果的精度进行比较。如图5 所示，使用经典罚函数法时，计算误差随着罚因子的增加呈先减小后增加的趋势，当M=50 时其数值精度最高，绝对误差平均值为5×10-4m。这表明在使用基于经典罚函数法构建的神经网络时，盲目的增大罚因子其效果可能适得其反。当罚因子M=1 时，L1精确罚函数法具有最好的求解精度，此时绝对误差平均值为5.2×10-4m。随着罚因子增大，其误差反而快速增加至与Lagrange 乘子法同数量级。对于本算例而言，Lagrange 乘子法的求解精度最低，绝对误差平均值达到1.4×10-2m，其原因正如引言中所提及的，Lagrange 乘子法建立的神经网络损失函数对应的Lagrange 函数在平衡点处的Hessian矩阵可能为非正定矩阵。本文建立的广义乘子法经过5 次参数更新之后，罚因子M=32 时绝对误差平均值减小至4.6×10-4m，5 次参数更新的详细情况参见表1。

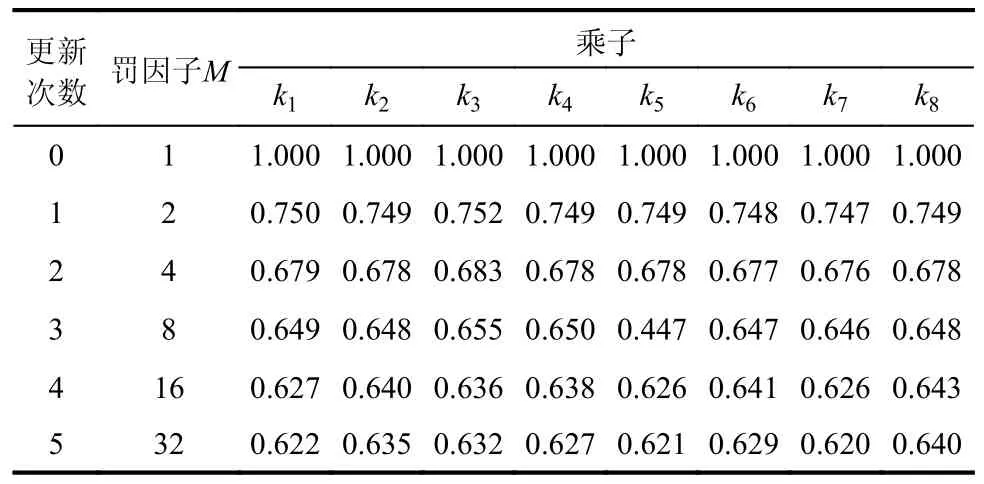
表1 Kirchhoff 薄板算例罚因子、乘子更新值Table 1 The updating of penalty factor and multipliers in Kirchhoff thin plate example

图5 四种神经网络模型挠度结果的绝对误差平均值Fig.5 Mean value of the absolute deflection errors resulted by four neural network models

以矩形简支薄板边界处的挠度计算结果为参考，进一步对经典罚函数法、L1精确罚函数法和本文算法进行比较。边界处挠度理论上为零，经典罚函数法罚因子M=50 时，挠度绝对值最小为6.1×10-4m；L1精确罚函数法罚因子M=1 时，挠度绝对值最小为4.2×10-4m；本文算法经过5 次参数更新后，挠度绝对值最小达到3.2×10-4m。本文算法求解出的薄板挠度云图如图6 所示，经典罚函数法、L1精确罚函数法和Lagrange 乘子法均可以获得与图6 接近的挠度分布，结果的主要区别在于计算精度。

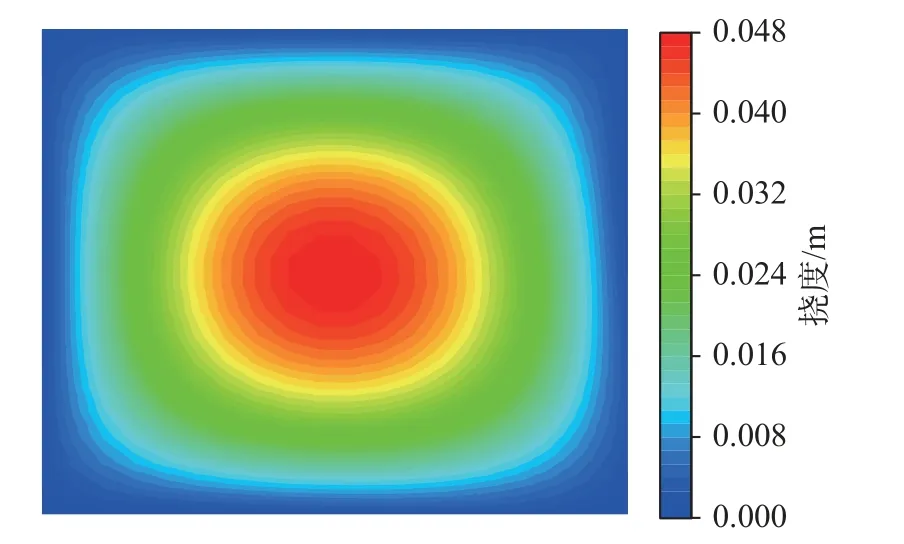
图6 本文算法求解的薄板挠度云图Fig.6 Deflect distribution of thin plate resulted by the proposed algorithm

基于上述比较分析，可以发现本文方法的求解精度整体上要优于其他方法。经典罚函数法和L1精确罚函数法，当罚因子取值合适时，求解精度与本文方法具有一定的可比性；若罚因子取值不合理，则计算结果误差较大。由于避开了罚因子的取值问题，因此本文方法的实用性强于罚函数法。

3.2 均布荷载作用下的简支梁

设有一受均布荷载作用的简支梁，如图7 所示，梁长l=1 m、梁宽b=0.01 m，梁高h=0.01 m，均布荷载q=10 N/m2，弹性模量E=1.0 GPa，求梁的挠度方程w(x)。

图7 平面简支梁示意图Fig.7 Diagram of a simple supported beam

该问题的控制方程为：

边界条件为：

使用广义乘子法构造的损失函数为：

使用本文涉及的四种不同神经网络进行求解时，神经网络拓扑结构均设定为1-1*10-1，优化器为Adam，学习率设定为0.01，域内配点数为10，边界配点数为2。基于3.1 节中算例求解的经验，使用罚函数时应避免罚因子取值过大，本算例执行时，经典罚函数法罚因子采用50 和100 两种取值，L1精确罚函数法的罚因子采用1 和50 两种取值。广义乘子法求解时初始设定为：罚因子M=5，乘子k1=k2=k3=k4=1，放大系数α=5，误差阈值ε=1×10-5，参数γ=0.25。Lagrange 乘子法的乘子初始值设定与广义乘子法保持一致。

四种神经网络求解得到的挠度曲线如图8 所示。经典罚函数法、Lagrange 乘子法和广义乘子法计算得到的挠度结果与解析解近乎完全重合，其绝对误差量级为10-4m。L1精确罚函数法计算所得的挠度结果误差则相对较大，其绝对误差量级为10-2m，这进一步证明了罚因子取值对基于罚函数法构建的神经网络求解结果的影响。

图8 采用不同神经网络计算的平面弯曲梁挠度曲线Fig.8 Deflection curve of plane bending beam by different neural network models

图9 给出了不同神经网络求解时的误差-耗时曲线。可以发现，由于数学理论的不同，四种神经网络求解过程呈现显著的差异。罚函数法的单次训练过程耗时较短，在向最终解逼近的过程中呈现反复的来回震荡现象，L1精确罚函数法的震荡幅度略小于经典罚函数法，但在本算例中由于罚因子取值不太合理所以误差无法继续降低。Lagrange 乘子法初期误差下降较快且无明显震荡，当误差下降至10-2m 量级后，其向最终解逼近时呈现逐步向下的来回震荡。本文采用的广义乘子法，经过4 次迭代后误差达到收敛标准。第一次迭代时耗时较长，原因在于初始值距离最终解较远，计算参数可能不合理。随迭代轮数增加，其计算参数将根据最终解的预测位置实时调整，后续迭代明显耗时减少。在向最终解逼近过程中，误差虽然也存在震荡现象，但每次震荡后误差均会大幅降低。比较四种神经网络求解该问题的耗时可发现，本文提出方法总耗时最少，与Lagrange 乘子法相比甚至呈现数量级的区别，因此在计算效率方面本文提出的方法明显优于其它的神经网络方法。

图9 采用不同神经网络计算的误差-耗时曲线Fig.9 Error and time-consuming curves by different neural network models

此算例求解时，广义乘子法神经网络求解4 次迭代过程中的参数更新情况如表2 所示。

表2 简支梁算例罚因子、乘子更新值Table 2 The updating of penalty factor and multipliers in simple supported beam example

4 广义乘子法神经网络求解的影响因素分析

4.1 神经网络拓扑结构对求解过程的影响

针对3.1 节中的Kirchhoff 薄板问题，构造隐藏层层数为1 层、2 层和3 层，每层神经元数量分别为10 个、20 个和30 个的神经网络，对其进行求解，观察神经网络拓扑结构对求解过程的影响。为简单起见将拓扑结构表示为2-L*N-1，其中，L为隐藏层层数，N为每层隐藏层的神经元数量，其他参数设置与3.1 节中保存一致。使用不同拓扑结构的神经网络进行求解，最终得到的误差耗时曲线如图10 所示。

图10 不同结构神经网络求解的误差-耗时曲线Fig.10 Error and time-consuming curves by different neural network structures

可以发现，隐藏层层数为1 层时，神经网络结果的绝对误差平均值均可收敛至10-3m 左右，增加隐藏层神经元数量可显著降低神经网络结果的误差。隐藏层层数为2 层时，隐藏层神经元数量增加对于降低神经网络结果的误差有一定作用，但是误差曲线在收敛过程中可能会产生较大振荡。隐藏层层数为3 层时，神经网络结果始终存在一定误差，而且该误差不会随着神经元数量的增加而减小。增加隐藏层层数与增加神经元数量都会导致求解耗时增加，但相对来说，隐藏层层数对计算效率影响更大。基于上述比较，可认为本文建立的广义乘子法神经网络求解偏微分方程时，过多的隐藏层层数反而会导致计算效率和求解精度降低。

4.2 配点数与隐藏层神经元数量

理论上，神经网络的计算精度与训练集的大小和隐藏层神经元数量密切相关。基于前面的分析，使用2-1*N-1 的神经网络拓扑结构，其中N=5、10、15、20、30、50，其他参数设置与3.1 节中保持一致，选取5×5、10×10、15×15、20×20、30×30 和50×50 等六种不同的配点方式，探讨不同配点数量在不同隐藏层神经元数量下的收敛情况，并将结果绘制于图11。

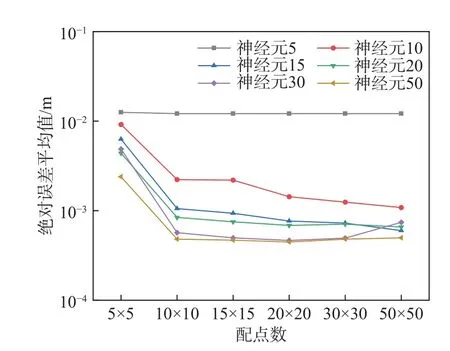
图11 不同配点数与隐藏层神经元数量组合求解的误差Fig.11 Error resulted by different combinations of collocation points and neurons in the hidden layer

可以发现，配点数为5×5 时，不同隐藏层神经元数量的神经网络求解结果的绝对误差平均值均较大；使用其他配点方式，当隐藏层神经元数量超过20 个时，神经网络求解结果的误差均能降低至10-3m 以下。因此，使用本文建立的广义乘子法神经网络求解偏微分方程时，配点数量不宜过少，且隐藏层神经元数量应达到一定标准。

5 结论

针对以往物理信息神经网络采用经典罚函数法进行求解时罚因子取值难以确定的问题，本文结合广义乘子法提出一种改进方法，经算例验证，可得出如下结论：

(1)与使用经典罚函数法、L1精确罚函数法和Lagrange 乘子法施加边界条件构造的神经网络相比，采用广义乘子法施加边界条件构造的神经网络具有更好的数值精度和更高的求解效率，而且求解过程更加稳定。

(2)使用本文提出的方法求解偏微分方程组时，神经网络隐藏层层数不宜过多。隐藏层层数设置合理的前提下，隐藏层神经元数量和配点数量均应达到一定标准。