基于深度学习和改进潮流介数的继电保护定值智能校验方法

韩学军

(国家电网有限公司华东分部，上海 200120)

随着“云大物移智链”新技术的快速发展，柔性直流、混合直流等新兴直流技术不断应用，数字革命与能源革命加速融合，给电网继电保护定值整定方面带来了新的机遇和挑战[1-3]。

在继电保护定值整定方向，基于行业整定规程，整定的方式有据可依，但同样由于规程规定的比较宽泛，在细节方面，不同整定业务人员理解见仁见智，其定值的选取也会不同。基于人工经验的整定过程在故障分析时，依靠人工对录波数据进行分析判别，需要大量的时间和精力才能对一次具体的故障进行正确判断，进一步剖析保护的动作情况是否正确，仍需保护人员对上下级所有线路及元件保护动作情况进行人工判别，效率较低[4-5]。有研究表明，近年来出现的诸多大停电事故主要是由于继电保护设备动作的逻辑性判断不正确造成的，如2018年3 月12 日的巴西欣古换流站断路器故障引起电网连锁大停电[6]，因此研究保护定值的智能化校核顺序就显得尤其重要[7-8]。

近年来，国内外众多专家学者对于在线保护定值的校核顺序展开了大量的研究，文献[9]给出了继电保护定值的在线校核概念和方法框架，并指出在线校核的重点是输电线路校核；之后，文献[10]针对电力系统组件化和网络化趋势，给出了并行运行的多代理系统保护定值在线校核预警系统，提高计算效率；随着对输电线路的日益重视，提高线路保护在线校核的效率，文献[11-13]提出了对输电线路重要度进行排序的潮流熵、电气介数的重要度指标；为了适应智能电网建设的需要，文献[14-15]从综合重要度的方面考虑，提出了网络关键程度和保护故障后果严重程度两个角度构建了保护重要度评估模型；文献[16-17]从方式变化影响域、故障排序以及最短路径搜索的思路出发，考虑了保护位置的短路电流、分支系数等继电保护定值计算故障量的变化率，确定保护定值的在线预警。

总体来说，目前对于继电保护定值在线校核过程中的线路优先顺序研究取得了较多的研究成果，但是这些成果尚未真正实现智能化和自动化程度较高的应用成效，此外，目前还没有看到有关将人工智能学习领域的相关研究理论应用至保护定值在线校核过程中。对此，本文提出了结合深度学习和改进潮流介数的继电保护定值在线智能排序优选方法。

继电保护定值校验的核心是判断线路的重要程度以及发生故障后对其他线路的影响程度。基于这两点，本文分别提出了有功无功潮流熵的线路重要程度判断方法、潮流冲击熵的影响程度判断方法。

1 有功无功潮流熵

电力系统输电线路中潮流包含有功潮流和无功潮流，传统输电线路重要程度的判断主要依靠有功潮流及其故障对其他线路冲击程度等的计算方式，具有局限性。为了进一步提高继电保护校验顺序精度，本文提出有功无功潮流熵的重要度判别方式。

传统信息熵是反映信息的不确定性、互相关性，对于电力系统输电线路发生故障导致潮流在其他输电线路的转移来说，该潮流熵就是在其他输电线路的冲击不确定性。该不确定性具有一定的混沌特性，对此，利用信息熵理论判断输电线路潮流转移的不确定性问题以及对其他线路造成的影响进行量化，从而辨识出重要线路，并为继电保护定值整定提供基础。

设X＝{x1，x2，…，xn}表示n个信息构成的向量，p(xi)(i＝1，2，…，n)表示信息xi的随机概率，则n个信息量构成的熵表示为[18]:

为了描述电力系统输电线路潮流的分布状态，采用式(1)中的信息熵来判断线路潮流无序性:

式中:wL表示电力系统Ns条输电线路的有功无功潮流系数，由式(3)定义；p(L)表示线路L潮流概率。

考虑到电力系统输电线路上的潮流由有功和无功构成，因而定义线路L有功无功潮流系数为:

式中:fPL和fQL分别表示有功潮流介数和无功潮流介数。下面给出潮流介数的介绍。

潮流介数[19]是在遵守基尔霍夫电压和电流定律下，以实际潮流为基础，度量发电与负荷之间走廊的脆弱情况，然而传统潮流介数只考虑了有功潮流，没有涉及无功潮流，对此予以改进。

传统潮流介数定义如下:

式中:P(m，n)表示发电机组m输送有功功率至负荷n；Pij(m，n)表示P(m，n)在输电过程中在线路ij上承担的有功功率；min(Sm，Sn)表示发电机视在功率Sm和负荷视在功率Sn的最小值。

通过式(4)的定义可见，传统潮流介数没有考虑输电线路有功和无功的共同作用，特别是若线路故障导致的有功无功潮流转移。因此，在式(4)基础上，分别定义有功和无功潮流指标:

式中:G表示发电机总数；N表示负荷总数；Pm和Qm分别表示发电机m有功功率和无功功率；Pn和Qn分别表示负荷n有功功率和无功功率；Qij(m，n)表示发电机m输送无功功率Q(m，n)至负荷Qn时在输电线路ij上流过的无功功率。

式(5)中的各个量Pij(m，n)、Qij(m，n)可采用传统潮流逆向追踪原理获得[19]。

通过定义式(5)输电线路重要度水平，并由此建立输电线路信息熵，即式(2)，可以判断电力系统中潮流的平衡程度，从而获得电力系统发生连锁故障的危险程度。

2 有功无功潮流转移量度指标

2.1 输电线路有功无功冲击度量指标

第1 部分能够度量潮流分布在电力系统中的分布状态，以此表明发生输电线路故障的危险程度。若输电线路发生故障，其潮流转移路径以及对其他线路的冲击程度需要进行度量。

设输电线路L在t时刻的有功潮流为，那么当输电线路L＇发生故障(故障时刻设为t+Δt)产生潮流转移ΔPL＇，由此在输电线路L上产生的潮流冲击为:

同理，与式(6)相同的无功潮流也将发生转移，对输电线路L产生冲击:

对于式(6)和式(7)的输电线路L来说，其有功潮流和无功潮流应该满足最大值约束:

由式(8)可见，若输电线路L上的有功和无功潮流发生冲击造成越限，将导致输电线路L故障和断线跳闸。

2.2 度量指标求解

输电线路故障有功潮流转移分布因子λt

PL实际是由于输电线路Lk＇-l＇发生故障导致的输电线路Lk-l上的有功潮流分配因子，其计算方式为:

式(12)中的ΔPk＇表示节点k＇有功注入的变化量，设t时刻该节点有功注入为Pk＇(t)，t+Δt时刻有功注入为Pk＇(t+Δt)，那么式(12)可以改写为:

对于输电线路Lk-l有功变化量实际是由电力系统中所有节点有功注入变化导致的，因此有:

3 继电保护定值智能校验

3.1 保护定值的校验排序

根据前述，当通过第1 部分获得了电力系统输电线路的信息熵后，可以判断出电力系统输电线路有功无功潮流分布状态，并推断系统发生有功无功潮流越限的危险程度。

同时，当通过第2 部分计算出了有功无功潮流转移度量指标后，可以判断出电力系统输电线路受到有功无功潮流转移的冲击影响。

由此可见，结合第1 部分和第2 部分，可以定义电力系统中输电线路L危险程度的排序:

3.2 基于深度学习的智能校验

由上述第1～2 部分叙述以及式(19)可见，保护定值的校验排序具有滞后性，即只有当系统运行之后，根据系统潮流获取得到线路的继电保护排序，无法做到超前警示及智能预估作用。对此，采用深度学习理论中的多层回归卷积神经网络予以解决。

卷积神经网络(Convolution Neural Network，CNN)是在传统神经网络基础上，加入卷积层、池化层、激励层、全连接层构成，对于空间范围内的输入数据具有良好的预测性能[20]，其基本结构如图1所示。

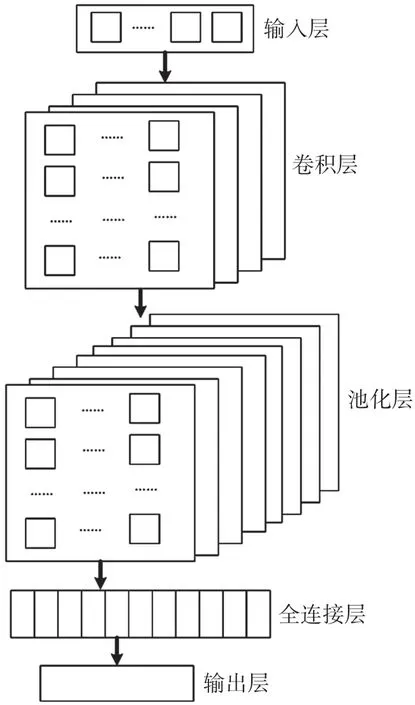
图1 CNN 结构图形

其卷积层的运算过程为:

通过式(20)获得特征输出维数较大，所以在池化层使用池化函数对高维特征向量求最优降维特征:

由上述结构可见，卷积神经网络是由多层神经元有机关联构成，能够提取局部特征、区域特征共享合并及二次优化等。

将卷积神经网络用于保护定值智能排序，建立该优化模型为:

式中:Xl表示第l层输入数据向量，主要指电力系统中各个输电线路有功潮流和无功潮流；yl为其输出结果，主要对应式(19)计算结果；ω表示支持向量机分类向量；b表示偏置量；λ表示卷积和池化层提取特征的系数；ξl和分别表示优化过程中的松弛量。

4 算例分析

采用图2 所示的IEEE57 节点系统对本文所提方法进行验证。

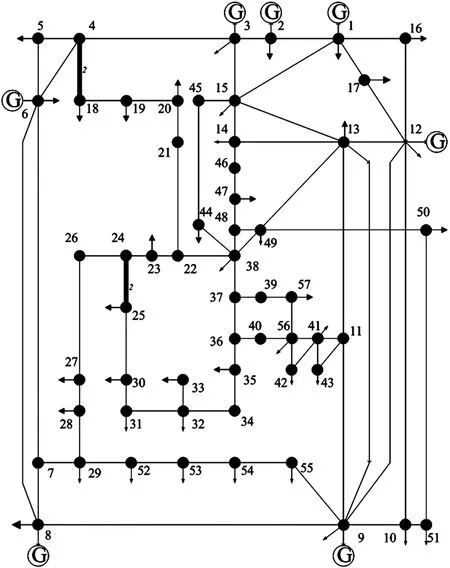
图2 IEEE57 节点系统结构

该系统共有57 个节点，包含7 个发电机节点(节点1 为平衡节点)和50 个负荷节点。该系统包含78 条输电线路(去除原4-18 和24-25 的双回线)，线路参数如表1 所示。

表1 线路参数(标幺值)

采用某地区2017 年5 月至9 月共5 个月的负荷数据。每个月选取1 天作为典型日，共5 天，每天以2 min 为间隔，共720 个的实际负荷。选取其作为潮流计算的实际负荷，共获得3 600 个潮流断面数据。这些潮流数据包含输电线路有功潮流、无功潮流、节点注入有功功率和无功功率(包含发电机有功出力和无功出力、负荷有功功率和无功功率)保存至数据库文件中，并以时间序列顺序依次命名。

将图2 所示的系统结构参数、输电线路上下限值、发电机启停限值数据作为常量保存至数据库中。

通过时间顺序的潮流数据，可以计算得到第一部分的信息熵，如表2 所示。

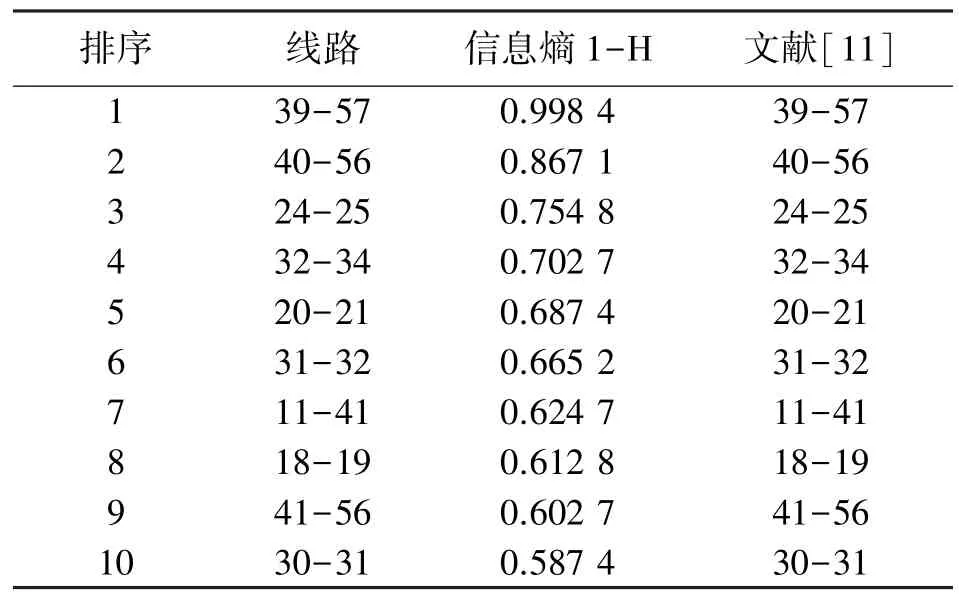
表2 某时间范围内潮流的信息熵

由表2 可见，采用信息熵的计算方法能够获得与文献[11]计算相同的输电线路重要度排序结果。根据该顺序可以依次获得重要度较大的输电线路潮流分布状态。当图2 显示系统发生线路故障导致潮流冲击影响时，进一步进行冲击度分析，并获得二者叠加的计算结果，其关键性顺序排序如表3 所示。

表3 综合信息熵和冲击度的重要线路

将线路的冲击影响因子与潮流信息熵综合作为支路重要度辨别指标结果，可得表4，由该表可见，受冲击影响，线路24-25 的重要度提升至排序1，其他变化不大。通过分析可见，线路24-25 上的潮流较重，节点25上的负荷较大，极易对系统产生较大冲击。

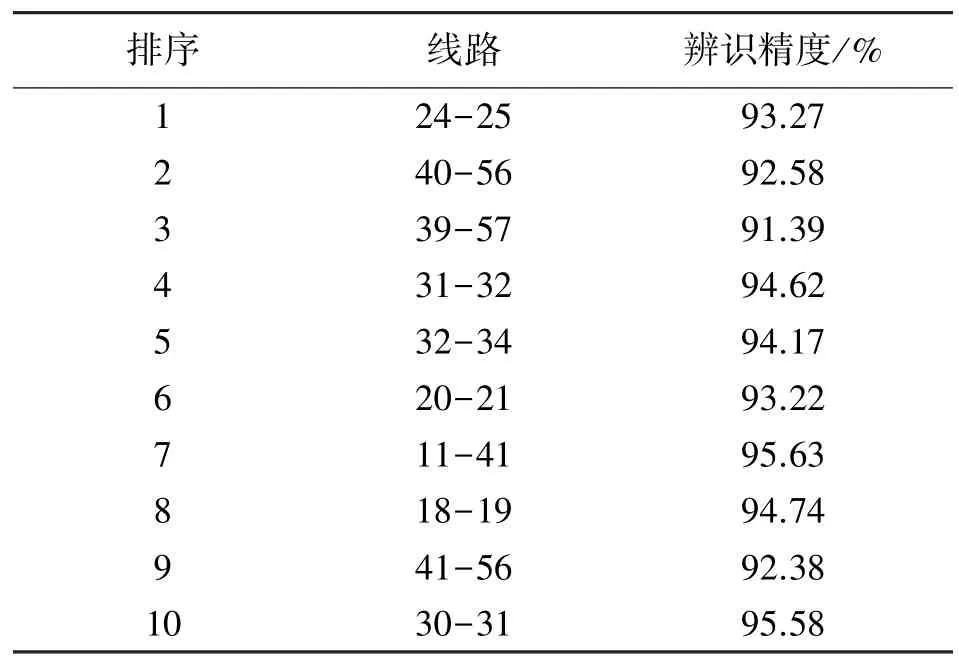
表4 卷积回归学习训练结果

为了能够实现本文第1 部分和第2 部分的计算，采用卷积神经网络进行回归学习，采用顺序时间内线路上的潮流、节点注入功率作为输入，采用综合辨识指标式(19)作为输出进行训练，可得辨识精度，结果如表4 所示。

表4 中卷积神经网络的训练集是以潮流断面时间窗口长度300 进行的，测试集采用连续的10 个时间断面进行测试，经过综合计算获得辨识精度，精度计算方法使用均方根误差计算方式。由表4 可见，重要度排序前10 的线路的辨识精度可达95%左右，由此可见，若超前预测或给定电力系统输电线路潮流数据，就可以获得重要线路排序，即可以获得继电保护定值的超前排序，对于快速应用于故障保护具有在线意义。

为了进一步验证本文算法，选取华东某实际电网对上述算法进行测试，在同等条件下，表4 中的辨识精度可达96%，进一步表明了所提方法的有效性。

5 结论

针对传统继电保护定值整定排序问题过度依赖人工计算方式问题，对传统潮流熵仅考虑有功功率以及线路有功功率冲击影响等进行改进，提出了有功功率和无功功率信息熵以及有功功率和无功功率线路冲击影响综合重要度排序模型，并使用卷积神经网络进行学习预测，体现了智能性、在线快速反应性。通过算例分析，验证了本文方法具有较高的线路重要度辨识精度，能够在线实现继电保护的智能校验顺序。