数字孪生变电设备的可校准热寿命损失评估方法研究*

陈韶昱，郑 翔*，周慧忠，杜奇伟，王海园，张海宁，陈亦然，李志明，徐小俊，冯 巍，杨士超

(1.国网浙江省电力有限公司衢州供电公司，浙江 衢州 324000；2.国网浙江省电力有限公司，浙江 杭州 310007；3.国电南京自动化股份有限公司，江苏 南京 211111)

数字孪生(Digital Twin)概念最早起源于上世纪六七十年代，契机是当时正在外太空执行飞行任务的阿波罗13 号飞船发生氧气罐爆炸。在这种远隔万里情况下，NASA 工程师们灵机一动，利用飞船传回的真实运行数据，在训练模拟器中调整环境参数以匹配航天器受损状况，最终成功找出解决方案，并帮助宇航员顺利返回地球[1]。由此数字孪生逐步发展为充分利用感知、仿真、控制、可视数据，集成多学科、多物理量、多尺度的融合与计算，以便于在虚拟数字化模型中更高效、更低成本地解决现实应用问题[2]。在新一轮电力体制改革的大背景推动下，变电设备的检修方式已经由传统的“计划检修”方式转为“状态检修”，而数字孪生技术能够为变电站向智能化转型提供最佳途径，基于在线监测数据、运行环境数据、工艺制造数据、以及离线试验/运维检修数据等多维度数据实现数字孪生变电设备运行状态和运行环境数据的全方位感知[3]。

电力变压器是变电站中的核心设备，特别是油浸式电力变压器，其以结构简单、运行可靠等优点，成为世界上应用最广泛的变电设备之一[4]。但变压器波动性过高的负载、电磁物理场，以及温度的变化使其老化状态十分复杂，变压器内绝缘的老化大致划分为热老化、电老化、机械老化和环境老化。由此引发的过载、局部过热，特别是热寿命损失现象，不仅加速了绝缘老化，严重甚至诱发匝间短路，造成大量经济损失[5]。

众多学者对数字孪生技术在以油浸式电力变压器为代表的变电设备中的应用展开了深入研究。文献分析表明数字孪生模型的构建主要是通过两类方法[6-7]实现的:基于模型驱动和基于数据驱动的方法。基于模型驱动的方法主要以工程采用的GB/T 1094.7—2008 和IEEE Standard C57.91—2011 标准中的经验公式[8]、热路等效法[9]，以及基于有限元[10]的数学方程方法为主，主要问题是很难针对变压器实体系统构建全面的、能契合其复杂性和实际性的物理模型，计算依据国标中热点温度对绕组热改性绝缘纸的相对老化率计算，考虑不够全面，得到结果可能大于实际寿命，存在安全隐患[11-12]。基于数据驱动的方法[13-14]主要以反向传播神经网络算法、极限学习机，以及支持向量机等机器学习方法为主，主要问题是机器学习中反复训练、迭代的过程只能基于拟合变压器长期的历史数据，虽然训练次数增加，输出结果的辨识精度无疑会很高，但考虑到多源异构数据的误差等级和可信度，以及动态退化的变压器系统，以上所涉及方法对于预测、评估变压器热寿命损失等功能可能不准确[15]。正因如此，学术界在数据驱动方法的框架内，研究者进行了诸多探索:将退化过程特征具有半马尔可夫协变量过程的比例风险模型应用于一般退化系统的最优替换问题[16]；基于嵌入序贯蒙特卡罗方法的状态空间模型技术，用于系统性能退化预测[17]；以及基于退化信号的确定性阈值预测模型、随机阈值预测模型和联合预测模型三种预测方法[18]等。然而，这些方法都不约而同地提升了数字孪生变压器系统的复杂程度。

由此，本文以油浸式电力变压器为例，提出了一种基于数字孪生变电设备的可校准热寿命损失评估方法，结合了前述数字孪生模型的两种构建要素，降低了对变压器运行历史数据以及机器学习要求，有效提升了GB/T 1094.7—2008 和IEEE Standard C57.91—2011 标准中经验公式应用于动态退化变压器系统中的热寿命预测准确性。该方法通过对构造数字孪生的多维度状态传感信息进行解析，获得关于变压器热寿命的多源异构数据，利用其中数据量丰富但误差等级稍差的实时监测数据构建初步评估模型，并进而利用数据量较少但误差等级较高的离线检测数据对如上的模型进行周期性校准。对处于中国浙江省Q 市某油浸式电力变压器为期两年的跟踪分析中表明，本文提出的评估方法，将该变压器热寿命损失评估的偏差降低至约5%，相比较于有关标准中经验公式约27%的预测偏差，本文所述方法有了显著提升。

1 方案设计

图1 为数字孪生变压器可校准热寿命损失评估的实验框图。基于某工程项目，我们对变电站油浸式电力变压器进行了在线监测及离线检测传感信息收集，通过数字孪生技术多状态、多维度地综合评估诸如定期检修时间、热寿命损失等要素，以提高变电站工作效率，节省生产成本。对变压器的在线监测，可以得到环境温度、顶层油温、负载变化、铁芯接地电流、放电量/次数/电位等信息；对变压器的离线检测，可以得到油纸聚合度(Degree of Polymerization，DP)、含水量、溶解气体(DAG)，如一氧化碳、二氧化碳、氢气等含量，以及糠醛(呋喃甲醛，一种呋喃类化合物)及其衍生物含量等信息。以上种种传感信息都可以从不同侧面评估热寿命损失，但其来源、误差等级、可信度，乃至数据结构、传输协议各不相同，是一组典型的多源异构数据[19]。

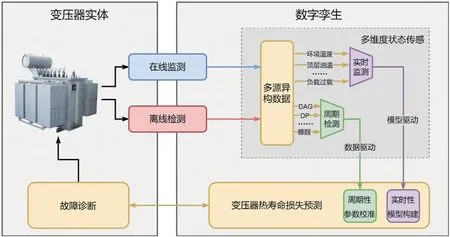
图1 数字孪生变压器可校准热寿命损失评估的实验框图

本文的研究工作就是将各种不同的数据信息进行综合，吸取不同数据源的特点，从多源异构数据提取实时监测信息，用于驱动构建变压器的数字孪生模型。这些信息可以来自于近乎实时的在线式传感器采样，比如间隔时长1 h 的状态记录，并因此受益于丰富的数据量，可以达成模型驱动的数字孪生模型构建，参见图1 中的子模块“实时性模块构建”，但由于涉及到众多厂商传感器不同的现场采集过程，故引入的传感误差较大，整体可信度偏低；同时这些信息也可以来自于周期性的离线式传感器采样，比如时间跨度6 个月的检测信息。这些信息大多数只能周期性停机进行采样，并因此受限于较少的数据量，但这类数据基本上来自于专业机构及其认证设备，故引入的传感误差可控，整体可信度较高。本文所提出的热寿命损失评估方法将此类信息用于驱动校准上述数字孪生模型，参见图1 中的子模块“周期性参数校准”，最终达成比单一实时性数据更好、更准确的热寿命损失评估预期。

2 数据采集

我们对某变电站油浸直冷式(Oil Natural Air Natural，ONAN)电力变压器进行了时间跨度为2 年的实时监测，采样间隔为1 h，如图2 所示，数据包括环境温度，采用AD590 晶体温度传感器，精度为1 ℃，参见图中最下方曲线，其明显呈季节性变化，平均最低气温约零下8 ℃，平均最高气温约38 ℃。顶层油温测量，采用铂电阻XMT-288F(c)型油面温度计，参见图中最上方曲线，其数值与前述的环境温度相关性较高，平均低点油温约16 ℃，平均高点油温约74 ℃，值得注意是第一年5 月15 日前后出现相对高点温度约89 ℃。通常由于受到绕组散热影响，变压器油整体向上浮动流向顶端，与空气进行热交换，降温后流入散热片底端，沉积在变压器油箱底部，整个散热过程中，在箱壁处变压器油贴近绕组和铁心等结构，因而其数值明显高于散热器平均温度，且低压绕组温度较高压绕组还要高一些，这也是一般采用顶层油温估算变压器热点温度的原因。负载系数即变压器平均输出的视在功率与变压器额定容量之比，参见图中中间部分曲线，平均值约45%，第一年5 月15 日前后同步出现相对高点负载，约112%。负载系数的数值在变压器额定容量的65%至75%最合适，过高则会使得绕组绝缘材料的寿命持续下降，累积效应会使绝缘纸失效。因此，业界一般通过变压器绕组热点温度评估变压器的绝缘老化寿命，即热寿命损失评估，其中的核心数据就是变压器绕组热点温度。

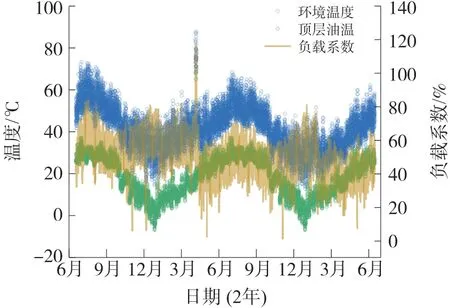
图2 时间跨度2 年的变压器状态实时监测数据

3 模型构建

绕组热点温度的数据来源可以是直接测量，例如在绕组上布置光纤传感器，但考虑到光纤传感器测温点与绕组的最热位置不一定吻合，以及本文所述变压器自身的传感功能缺失，我们采用的是对绕组热点温度的间接传感测量方法，其数据来源便捷但整体可信度偏低。通常变压器在实际运行中，不同时刻有着不同的负载率，与之对应的内部状态也是不一样的。利用负载率与热点温度换算模型，可以将不同负载率的热源计算结果导入数字孪生模型，估算不同负载率下的热点温度。IEC 60076-7—2005 电力变压器第7 部分:油浸电力变压器加载指南[20]，给出了额定负载下的油浸式变压器各部分温升的计算方法，并指出负载系数K、环境温度θa、变压器顶层油温升Δθ顶层、变压器绕组的温升Δθ绕组等参数对绕组热点温度θh影响大，具体有θh＝θa+Δθ顶层+Δθ绕组，Δθ顶层、Δθ绕组可由式(1)计算。

式中:Δθor为顶层油温升；R为额定电流下负载损耗与空气损耗的比值；H为热点系数；x为油指数；y为绕组指数；gr为额定电流下绕组平均温度对变压器油平均温度的梯度。以上各参数可根据冷却方式确定其大小，例如，对于ONAN 型变压器，Δθor＝52，R＝6，H＝1.3，x＝0.8，y＝1.3，gr＝14.5。将图2 中观测所得的数据代入计算可得该变压器运行时段内的绕组热点温度分布，参见图3 中稠密曲线，其中第一年5 月15 日前后出现相对高点温度，约122 ℃。

图3 变压器绕组热点温度计算数据与热寿命损失估算

由国标可知，采样n时刻热老化率V与绕组热点温度θh的关系可由式(2)计算。变压器热点温度在98 ℃以下时，其相对热老化率为1。绕组热点温度超过98 ℃时，相对热老化率上升剧烈，如图3 所示，当热点温度超过122 ℃时，相对热老化率高至16，如若持续时间为1 h 则变压器热寿命损失可高达16 h。

式中:S为变压器出厂时设置的使用寿命，T为变压器的剩余寿命，Δt是变压器工作在当前热点温度下的持续时间。当变压器绕组温度在80 ℃～130 ℃范围内，老化率温度变化系数P是蒙辛格公式中的常数，国标中的相应计算令P＝6，也称之为6 ℃法则，即温度每升高6 ℃，变压器绝缘寿命就降低一半。由此可以推导该变压器的热寿命损失曲线，参见图3 中单条曲线，在2 年的运行阶段中，由于温度导致的变压器老化效应，不断在工作状态中进行累积，最终其热寿命损失累计超过了15 d，尤其是第一年5 月15 日前后出现高点温度，直接导致变压器的热寿命损失超过5 d。

4 模型校准

工程实践经验往往证明变压器的绝缘老化寿命很难用一个相对简单的关于绕组热点温度及固定等于6 的老化率温度变化系数进行定量描述与分析。除了前述传感误差较大，整体可信度偏低的原因，变压器的工作状态也处在不断的动态衰减过程中，绕组绝缘温度分布不均匀，相对老化率不能以高温运行条件下最严重的老化情况作为参考。基于图2 的变压器状态实时监测数据，采用不同的老化率温度变化系数P对文中所述变压器进行了热寿命评估，详见图4 老化率温度变化系数的取值对热寿命损失估算的影响，其中P的取值由5.00 至7.00，分析结果表明时间跨度2 年后，对应P＝7.00 的曲线，出现热寿命损失评估的极大值Lmax，为20.54 d；对应P＝5.00 的曲线，出现热寿命损失评估的极小值Lmin，为14.09 d，两者偏差超过45%，这无疑会对随后变压器的故障诊断带来不确定性的干扰。

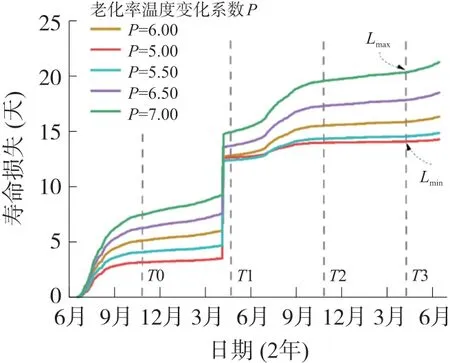
图4 老化率温度变化系数的取值对热寿命损失估算的影响

由此，本文提出并验证了一种基于化学特征参量的DGA 检测信息对原有的基于国标6 ℃法则数字孪生的模型进行周期性校准的方法。电、热等作用导致的变压器老化效应使得其内部绝缘材料的纤维素产生裂解，最终分解成CO 和CO2和糠醛，由GB/T 7252—2001《变压器油中溶解气体分析和判断导则》中的三比值法就可以判断变压器绝缘的状况。DGA 通常采用定期检测的方法，每隔一定的时间试验人员将现场采集到的油样送到试验室中进行分析，用安置在试验室或现场的气体色谱仪得到检验结果[22]，此外诸如水分、糠醛等检测值也列入了国家标准，比如DL/T596—1996《电力设备预防性试验》。但不可否认的是，离线检测工作量大，程序复杂，检测周期较长，运行人员无法实时掌握变压器运行情况。

DP 是用于评估变压器寿命损失最为可靠的参数，其数值可以直观表征该大分子中单体葡萄糖分子的数目，对应着油纸的绝缘水平。变压器油纸绝缘聚合度下降与老化速率k1的关系为1/DPt-1/DP0＝k1t，其中DP0为初始的绝缘聚合度，DPt为t时刻的绝缘聚合度[23]。但DP 的定量分析步骤繁杂，具体步骤参照GB 1548—2006 执行，严重影响了变压器数字孪生建模的效率，因而在实际工程上通常采用DGA检测信息中CO2与DP 之间较高的线性相关度[24]，或者由糠醛含量进行变压器DP 值预测[25-26]，进而从k1值和DP 阈值计算变压器剩余运行年限。式(3)所示为一种以DP 作为参量的评估变压器寿命的方法[27]，其中η为特征寿命，F为DP 的下限值，C0为油纸中初始含水量，T为温度，A、B是与待测变压器相关的待定常数，可由经验确定。

如图3 及图4 所示，变压器DGA/糠醛的离线检测分别在如下时刻进行:T0(第一年11 月15 日)、T1(第二年5 月15 日)、T2(第二年11 月15 日)，以及T3(第三年5 月15 日)。根据前述研究成果[21-25]，本文计算了如上时间节点的待测变压器的寿命损失，T0时刻寿命损失＝10.83 d；T1 时刻寿命损失18.66 d；T2 时刻寿命损失＝20.76 d；T3 时刻寿命损失＝21.91 d。这些DGA/糠醛传感信息的测量来之不易，但其精准度要远高于对绕组热点温度的间接推算或直接测量。在本文中被用于校准基于热点温升变压器绝缘寿命损失模型的老化率温度变化系数P，使其不再是一个恒等于6 的常数。此外，变压器运行环境的不稳定也会使CO、CO2和糠醛的含量在测量周期内有较大的波动，这也是需要周期性校准数字孪生模型的重要原因。

5 评估验证

如上所述，在T0～T3 时刻基于化学特征参量得到的寿命损失数值，被用于分段校准由式(2)得到的原始热点温升的寿命损失模型，分析表明当P取5.63～8.24 的一系列数值，能更准确地对应不同的绝缘老化类型，并较好地预测变压器热寿命损失。图5所示为周期性校准后的老化率温度变化系数取值及热寿命损失估算，其中最下方线段表示未经校准P0＝6.00 的寿命损失模型用于对比，此模型在T0～T3 时刻得到的寿命损失预测记为，以及前上方线段表示校准后的T0 时刻前的热寿命损失模型，此时对应式(2)修正了老化率温度变化系数，即P1＝8.24；T0～T1 上方曲线表示校准后的T0～T1 周期内的热寿命损失模型，此时P2 ＝7.55；T1～T2 上方线段表示校准后的T1～T2 周期内的热寿命损失模型，此时P3 ＝5.63；T2～T3 上方线段表示校准后的T2～T3 周期内的热寿命损失模型，此时P4＝7.26。总体而言，校准后的热寿命损失模型较之前的模型，反映出了变压器更为严峻的老化趋势，直接原因是本文所提的校准后的热寿命损失模型考虑了更多的老化因素与表征，多源异构的处理提升了变压器数字孪生模型的精准性。

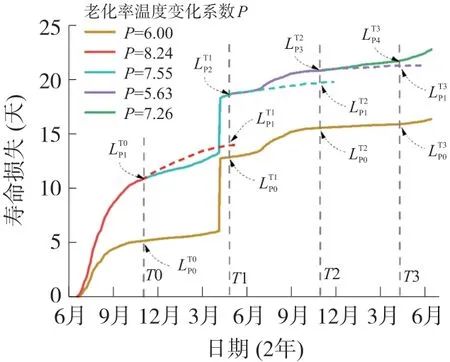
图5 周期性校准后的老化率温度变化系数取值及热寿命损失估算

在此基础之上，本文进一步验证了如上方法对变压器系统寿命损失预测的准确度，尤其是中、短时间跨度，比如6 个月后的寿命损失预测，这类研究在文献[13-18]所述的基于数据驱动的变压器数字孪生方式中鲜有报道，其中根本原因在于变压器工作状态的短期波动难以预测及拟合。我们采用的验证方式是对前文所述的周期性校准的热寿命损失模型，进行非线性拟合并延展至对应预测时刻，比如对位于T0 时刻以前，校准后的热寿命损失模型，即图5 中最下方线段，进行了非线性拟合并延展至T1时刻，详见图5 中T0～T1 上方虚线，其表示为基于第一年11 月15 日之前的运行数据对该变压器中、短时间跨度的寿命预测评估。T0～T1 上方虚线在T1 时刻采样得到代表了基于P1 ＝8.24 寿命损失曲线6 个月后的预测值，以此类似得到，与之对应的未经校准的寿命评估值参见图5 中最下方线段中的本文采取的非线性拟合为Boltzmann 函数曲线拟合方式，以达成各节点的试验值与拟合值的偏差平方和为最小。拟合参数如表1所示，表中同时给出了T1～T2 虚线/T2～T3 虚线的拟合参数，其含义可参见相应的定义。

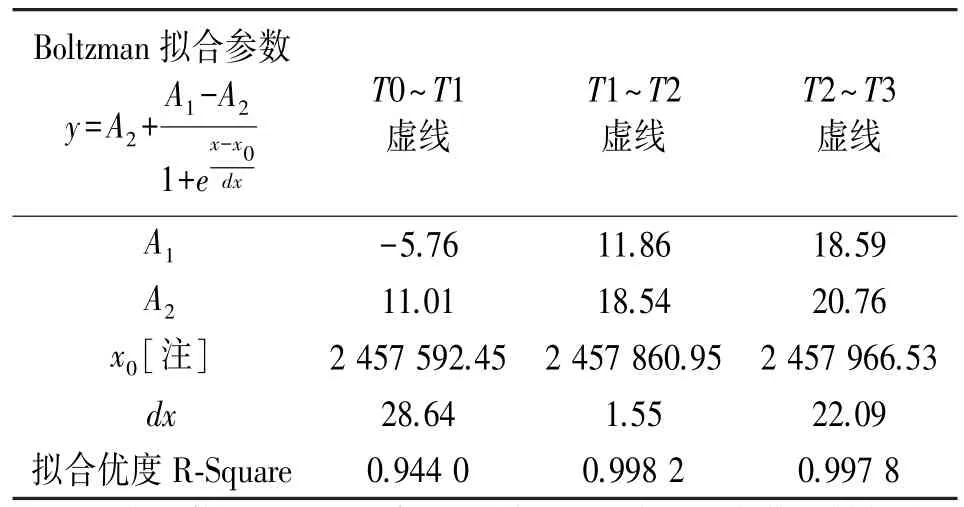
表1 校准后变压器热寿命损失预测拟合曲线参数

图6 所示数据分析表明，T1 时刻经典模型的预测偏差度约30%，校准后的预测偏差度约31%，两者相差不大，但值得注意的是经典模型的预测是基于T1 时刻之前的变压器运行数据，而校准后的预测仅仅是基于T0 时刻之前的数据，两者相比高下立判，校准后的预测模型在近似偏差度的情况下只需要差不多一半数量的变压器运行数据；T2 时刻经典模型的预测偏差度约25%，校准后的预测偏差度约10%，两者相差逐步增大；T3 时刻经典模型的预测偏差度约27%，校准后的预测偏差度约5%，两者相差显著，由此可见本文所提出的可校准热寿命损失评估方法较经典模型更为准确。

图6 中、短时间跨度热寿命损失预测偏差度

6 结束语

本文围绕数字孪生变电设备的可校准热寿命损失评估方法展开研究，以油浸式电力变压器为例，提出并验证了一种基于化学特征参量的DGA 检测信息对原有的基于国标6 ℃法则数字孪生的模型进行周期性校准的方法。降低了对变压器运行历史数据以及机器学习要求，有效提升了GB/T 1094.7—2008 和IEEE Standard C57.91—2011 标准中经验公式应用于动态退化变压器系统中的热寿命预测准确性。对处于中国浙江省Q 市某油浸式电力变压器为期两年的跟踪分析中表明，本文提出的评估方法，将该变压器热寿命损失评估的偏差降低至约5%，相比较于有关标准中经验公式约27%的预测偏差，本文所述方法有了显著提升。评估方法在二次设备健康状态评估中也得到了应用，并有显著效果。