基于MILP 的PICO 算法差分和线性区分器的搜索*

石康康，任炯炯，陈少真

战略支援部队信息工程大学，郑州450001

1 引言

伴随着物联网的快速发展，以智能卡为代表的资源受限设备得到了广泛的应用.在这些设备上，传统密码算法面临着硬件实现成本高和电量耗费大等问题，为此，轻量级分组密码算法应运而生，并逐渐成为了当前密码领域讨论最为活跃的热点之一.差分分析[1]和线性分析[2]作为当前应用最为广泛的密码分析方法，在密码分析过程中，毫无例外都需要寻找有效的区分器，即具有高概率或者高相关度的攻击路径.手动搜索的方法固然可行，但面临着计算量大、效率低、耗时长、仅能给出部分条数区分器等诸多缺点，一批利用自动化搜索技术来寻找区分器的相关工具因此涌现出来，主要包括混合整数线性规划(MILP)[3-5]和布尔可满足问题(SAT)[6-8]等.

MILP 是一类在一定约束条件下求解目标函数最值的优化问题.该技术最早由Mouha 等人[3]引入到密码分析中，通过MILP 面向字节建模实现了最少活跃S 盒个数的自动化计算.随后，Sun 等人[4]在ASIACRYPT 2014 上对该技术进行了扩展，给出了基于比特级操作的更加精细的MILP 搜索模型.在FSE 2016 会议上，Fu 等人[5]将MILP 技术应用于ARX 密码中的差分特征和线性逼近的自动化搜索.目前，该方法已应用于多种区分器的搜索，并取得了显著成效.

为满足物联网应用的需求，Bansod 等人在2016 年提出了轻量级分组密码PICO 算法[9]，PICO 算法是一种基于替换和排列的SPN 结构的分组密码.2017 年，马楚焱等人[10]利用MILP 模型找到大量7轮零相关线性逼近，并实现了10 轮密钥恢复攻击.2019 年，Kumar 等人[11]基于分支定界的方法搜索到一条概率为2-63的21 轮差分区分器.2020 年刘宗甫等人[12]基于MILP 模型找到了10 轮积分区分器，并利用9 轮积分区分器实现了11 轮密钥恢复攻击.2021 年，赵晨曦[13]首次使用不可能差分对PICO 算法进行评估，并构造了7 轮不可能差分区分器.

本文主要利用MILP 自动化搜索模型，进一步评估和分析了PICO 算法的抗差分分析和线性分析的能力.首先利用不等式组对PICO 算法各组件的差分特征和线性掩码的传播规律进行了精细的等价描述.其次，利用S 盒的扩散特性以及置换层的传播特性，对轮函数活跃S 盒数目进行了限制，极大缩小了搜索空间，进而提出了针对PICO 的两步MILP 搜索算法.对于差分区分器的搜索，得到了4 条概率为2-63的21 轮差分区分器，其中3 条异于文献[11] 中提出的差分路径;对于线性区分器的搜索，首次得到3 条相关度为2-30的20 轮线性区分器.与已有结果的对比如表1 所示.

表1 PICO 算法区分器的搜索结果Table 1 Search results of PICO algorithm distinguishers

本文的其余部分组织如下.第2 节为必要的准备工作，简要介绍相关符号、PICO 算法的加密流程与MILP 模型;第3 节详细描述PICO 算法组件差分特征的刻画以及对模型的优化，之后实现对PICO 算法最优概率差分区分器的搜索;第4 节介绍各组件线性逼近的不等式描述及优化方法，并对PICO 算法最优相关度线性区分器进行了搜索;最后第5 节总结本文的方法与结论.

2 准备工作

2.1 符号说明

Q为上的非空子集，记CQ为完全刻画非空子集Q的线性不等式的集合，即CQ作为一个线性不等式组的解集为Q.Prec(u) 定义为集合|，其中表示xi ≤ui，i0，1，···，n-1.

2.2 PICO 算法

PICO 算法是由Bansod 等人[9]在2016 年提出的一种基于替换和排列的SPN 结构的轻量级分组密码，支持64 比特的分组长度和128 比特的密钥长度，共有32 轮.PICO 算法的轮函数由三个部分组成:轮密钥加、列替换和置换层.算法整体结构如图1.

对于轮函数输入的64 比特输入状态Pi，将其排列为4×16 的矩阵形式表示，其中表示输入状态Pi的第j比特元素，状态矩阵表示如下:

轮密钥加:将各轮输入状态Pi对应的矩阵和轮子密钥RKi对应的矩阵按相应比特进行异或操作.PICO 算法的密钥扩展算法类似于SPECK 算法，轮子密钥的提取过程如下:

提取到RK0和L1后，重复如下过程32 次，取j0，1，···，31，得到其余轮子密钥:

(1)L2(RKi ⊕(L1⋙3))⊕L1;

(2) RKj+1(L2⊕(RKj⋘7))⊕j;

(3)L1L2.

列替换:列替换是对矩阵的每一列的四个比特作为S 盒的输入，得到的四个比特的输出值对该列进行替换，可以描述为:

其中，PICO 算法使用了可逆的4 位S 盒.在十六进制表示法中，S 盒的作用在表2 中给出.

表2 PICO 算法的S 盒Table 2 S-box of PICO algorithm

置换层:PICO 算法的置换层是将状态矩阵的第i行第j列的元素赋值到新状态矩阵中对应位置.因为状态矩阵中的元素对应于64 比特输入向量的特定比特位，故转化为对应比特位的置换操作如表3.

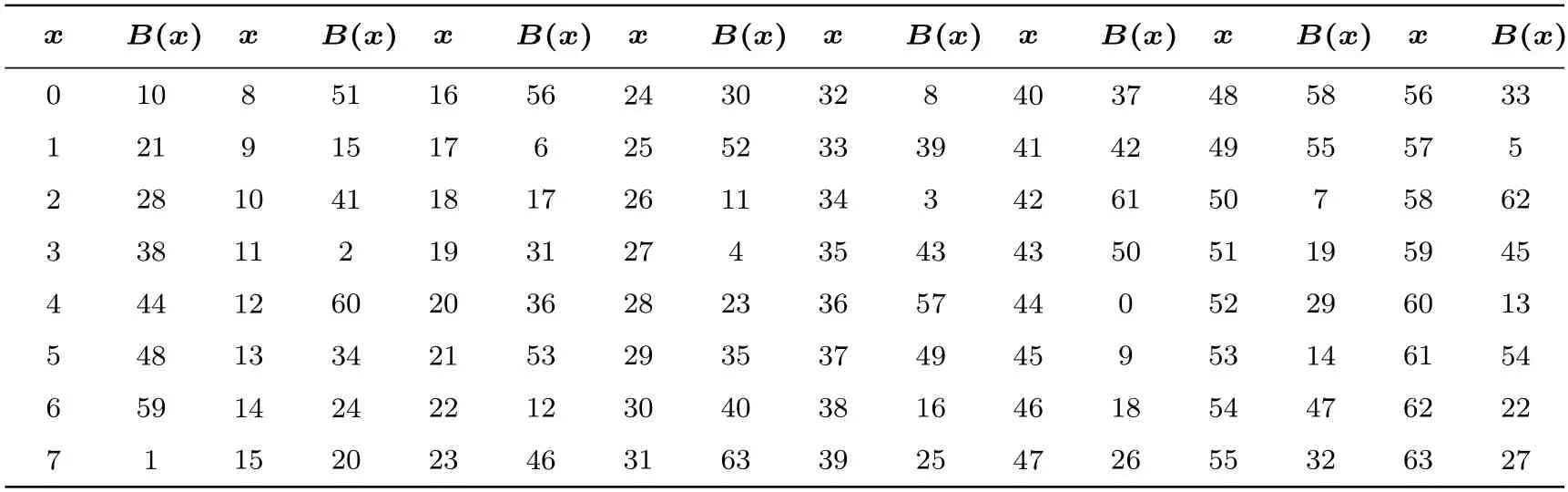
表3 PICO 算法的比特置换Table 3 Bit permutation of PICO algorithm

2.3 基于MILP 的差分特征和线性逼近的搜索算法

在MILP 模型建立中，重点和难点是将密码算法的各部件转化为线性关系.在此基础上可以对这些线性关系进行适当的优化，从而更加精确地划定搜索空间，加快对MILP 模型的求解速度.目前，求解这类问题有很多成熟的商业软件，例如Gurobi[14]等.本节简单回顾一下Sun 等人[4]提出的算法及本文所采用的主要框架模型.

2.3.1 S 盒差分和线性的传播特性

Sun 等人在2014 年提出了基于比特级操作的MILP 模型[4]，旨在寻找差分特征和线性逼近中活跃S盒的最小数目，并提出了非线性组件S 盒的数学描述方式.

S 盒差分特征的数学描述:对于一个w×v规模的S 盒，假设(x0，x1，···，xw-1)和(y0，y1，···，yv-1)分别是它的输入和输出差分.并用二元变量At来表示该S 盒是否活跃，At1 当且仅当输入差分x0，x1，···，xw-1不全为0，有

Sun 提出了利用差分模式(x，y)(x0，x1，···，xw-1，y0，y1，···，yv-1) 来表示S 盒的差分分布情况，这样可以通过离散点集对S 盒的差分性质进行刻画.通过使用SageMath[15]中的inequality.generator()函数推导出凸包的H-表示[5]，然后用贪心算法[5]来移除大量冗余的不等式.基于上述操作，便可以使用少量的线性不等式来精确描述S 盒的差分特性.最终通过设置目标函数为活跃S 盒个数，并使用Gurobi进行求解.

S 盒线性逼近的数学描述:S 盒基于MILP 的线性逼近模型与差分特征模型具有对偶性质.对于一个w×v规模的S 盒，假设(x0，x1，···，xw-1) 和(y0，y1，···，yv-1) 分别是它的输入和输出掩码.同样用二元变量At来表示该S 盒是否活跃，此时At1 当且仅当输出掩码y0，y1，···，yv-1不全为0，有

令线性模式(x，y)(x0，x1，···，xw-1，y0，y1，···，yv-1) 来表示S 盒的线性逼近表.类似地，精确描述S 盒差分特征的刻画方式同样适用于对S 盒线性逼近的刻画.

2.3.2 S 盒的高效建模算法

Boura 等人在文献[16] 中提出，对于已经生成的不等式组，可以通过简单地将一些线性不等式相加，就可以从这个初始集计算出许多其他线性不等式.显然，这些不等式依然包含原有的差分和线性模式.这样做的目的是为了生成比凸包不等式更有意义的不等式，其中有意义意味着新不等式比初始不等式消除了更多不可能的差分对或线性对.对此，他们提出了不等式扩充算法，如算法1 所示.

此外，Boura 等人提出了两种新的S 盒建模方法(文献[16] 中的算法2 和算法3).两种算法分别将S 盒的不可能差分或线性模式划分为a⊕Prec(u) 形式的集合和变形球形式的集合，两种形式都可以提供一个单独的不等式来移除集合中的所有点集.

不等式规模的大小直接决定了求解的效率，因此约减算法是十分必要的.由于贪心算法不能保证解的最优性，这使得贪心算法得到的不等式组对S 盒性质的刻画依然不够精确.因此，Sasaki 等人在文献[17]中提出了基于MILP 的约减算法，即算法2.该算法继承了MILP 模型的优点，并可以得到最优解.

2.3.3 基于MILP 的两步搜索算法

2019 年，Zhu 等人[18]在CT-RSA 上根据过往的分组密码差分路线搜索研究，提出了基于MILP 的两步搜索模型，旨在搜索GIFT 的最优差分路径.其基本思路为建立交互的两层算法，分为内层和外层.在算法的外层，目的是搜索包含活跃S 盒数目最少的截断差分路径;在算法的内层，以外层搜索的截断差分路径作为约束条件，目的是搜索概率最高的比特级差分路径.算法循环执行外层与内层，在对外层的搜索空间施加限制后，保证了对所有包含活跃S 盒数目尽量少的截断差分路径下的最高概率比特级差分路径的搜索，故可以搜索到最优差分路径.

本文结合PICO 算法组件和算法结构的特点，对基于MILP 的两步搜索模型进行了改进，实现对PICO 算法最优差分和线性区分器的搜索.

3 PICO 算法最优差分路径的搜索

本节结合PICO 算法结构特点，利用MILP 的两步搜索模型对PICO 的最优差分路径进行了搜索.基本思路为: 建立循环嵌套的外MILP 模型和内MILP 模型.在外MILP 模型中，每次搜索活跃S 盒数目最少的截断差分路径;在内MILP 模型中，搜索该截断差分路径下概率最大的比特级差分路径.

3.1 PICO 算法MILP 差分模型的建立

PICO 算法的列替换可视为两个置换操作和一个S 盒操作的组合，置换层视为比特级的置换操作，因此PICO 算法只包含2 个组件: 置换操作和S 盒.在考虑差分在轮函数的传播过程中，由于置换操作只改变了差分比特的位置，因此只需着重刻画S 盒的差分传播规律.

记ai，j为第i轮第j个S 盒Si，j的状态.设Si，j的输入和输出差分分别为和若输入差分非零，那么记为活跃S 盒，有

对于S 盒的差分特性而言，首先计算PICO 算法S 盒的差分分布表.

外MILP 模型对S 盒的刻画: 外MILP 模型搜索活跃S 盒数目最少的截断差分路径，故目标函数为

对于S 盒的差分分布表，可以由差分模式(x0，x1，x2，x3，y0，y1，y2，y3) 进行表示.根据差分模式的扩散概率是否为零，将其划分为差分集合Q1和首先对Q1利用SageMath 生成S 盒的凸包不等式，并对利用文献[16] 中的算法2 和算法3 生成性质较好的不等式集合，将它们作为S 盒初始的刻画空间.为寻找性质更好的不等式，对使用算法1 进行扩充.为降低不等式组的规模，实现以尽量少的不等式数量来高效刻画S 盒.为此，使用算法2 对进行约减，成功将不等式组的规模降至16 个(见表4)，将这16 个不等式应用于PICO 算法外MILP 模型对S 盒差分性质的刻画.

表4 PICO 算法差分模型中S 盒差分性质的刻画Table 4 Characterization of S-box differential properties in differential model of PICO algorithm

内MILP 模型对S 盒的刻画:在搜索到截断差分路径后，在此基础上以高概率为目标，寻找比特级差分路径，因此需要概率大小加入到内MILP 模型中.PICO 算法S 盒差分分布表中的非零值为2、4 和16，因此在外MILP 的基础上了另外添加两个分量(p0，p1) 来刻画S 盒的差分性质，对应关系如下:

因为内MILP 模型搜索的是高概率的差分路径，而概率乘积的最大值等价于每个S 盒的概率值的指数和的最大值，由于差分分布的概率指数部分全为负数，故可转换为求指数之和的最小值，即

对所有概率非零的差分模式，可以由离散点(x0，x1，x2，x3，y0，y1，y2，y3，p0，p1)进行刻画，并将其作为集合Q2，记集合-Q2.类似外MILP 模型的步骤，我们成功将不等式组的规模降至19 个(见表4)，应用于PICO 算法内MILP 模型对S 盒差分性质的刻画.

3.2 PICO 算法最优差分区分器的搜索结果

基于上述刻画，可以初步实现对PICO 算法差分区分器的搜索.但伴随着轮数的增加，生成的不等式及变量的数目也随之增多，求解速度也会变慢.为此，本节对PICO 算法的差分模型进行了优化.

在对PICO 算法模型的优化过程中，首先考虑的是对变量数量的优化.在PICO 算法的轮函数中，在通过S 盒之前和之后均需要经过一次置换操作，因此，根据置换操作中一一对应关系，S 盒的输入差分和输出差分均可以由各轮的输入差分来表示.此时，外MILP 模型中的变量只包含各轮的输入差分，极大地减少了变量的个数.其次对轮函数中的活跃S 盒数目进行了约束.在对PICO 差分区分器的搜索结果进行分析之后，发现对于任何一个高概率差分路径，其轮函数的活跃S 盒数目不超过2 个.通常来说，若本轮活跃S 盒数目过多，经过置换操作以后，差分比特不可避免地扩散到下一轮不同S 盒的输入差分，从而造成更多活跃S 盒，导致差分路径成立的概率也不会很高.因此，在约束条件中额外限定了轮函数中活跃S 盒的数目不超过2.经过实际运行测试，模型的求解速度较之前有了极大程度的提升.除此之外，通过大量实验发现，当差分路径中活跃S 盒数目比相同轮数路径的最小活跃S 盒数目多3 个时，该差分路径概率最大成立的概率可视为0.因此，针对某一特定轮数，记该轮数下最小活跃S 盒数目为Mr，遍历搜索活跃S 盒数目[Mr，Mr+2] 的所有差分路径，其中概率最大的差分路径为该轮数下的最优差分路径.通过对组件差分性质的刻画及模型的优化，我们建立了PICO 算法的基于MILP 的两步搜索模型的差分区分器搜索算法，具体步骤如算法3 所示.

利用该算法，对PICO 算法的尽可能长轮数的差分区分器进行了搜索.对于21 轮差分区分器的搜索，算法3 找到了4 条概率为2-63的差分区分器，其中一条同文献[11] 中提出的路径相同，其余3 条新的差分路径见表5(从左至右是从高比特位至低比特位).由于在搜索过程中，我们对轮函数的活跃S 盒个数进行了限制，并遍历搜索了与最小活跃S 盒数目差值在2 个以内的所有差分路径，经过前期的实验数据分析，该算法能以较大的概率搜到所有的最优差分区分器.

表5 PICO 算法新的3 条21 轮差分区分器Table 5 Three new 21-round differential distinguishers for PICO algorithm

4 PICO 算法最优线性路径的搜索

本节基于第3 节的基本结构，对算法3 的刻画形式进行了改进.基于MILP 的两步搜索模型，精确刻画了PICO 算法主要组件的线性逼近的传播规律，并结合SPN 结构下S 盒特性对模型进行了优化，最后对PICO 算法的最优线性区分器进行了搜索.

4.1 PICO 算法MILP 线性模型的建立

因为对置换操作的刻画可以很容易根据相应的位给出等式约束，因此不再进行详细叙述.

对于 S 盒操作，记ai，j为第i轮第j个 S 盒Si，j的状态.设Si，j的输入掩码为输出掩码为若输出掩码非零，那么记为活跃S 盒，有

对于S 盒的线性特性而言，首先计算PICO 算法S 盒的线性逼近表.

外MILP 模型对S 盒的刻画:外MILP 模型目标为搜索活跃S 盒数目最少的路径，因此目标函数为

对于S 盒的线性逼近表，可以由线性模式(x0，x1，x2，x3，y0，y1，y2，y3) 进行表示.根据线性模式的偏差是否为零，将其划分为线性集合Q3和不可能线性集合类似，利用SageMath，文献[16] 中的算法2 和算法3 生成S 盒的刻画空间并使用算法1 对进行扩充以及算法2 进行约减，最后成功将不等式组的规模降至14 个(见表6)，将这14 个不等式应用于PICO 算法外MILP 模型对S 盒线性性质的刻画.

表6 PICO 算法线性模型中S 盒线性性质的刻画Table 6 Characterization of S-box linear properties in linear model of PICO algorithm

内MILP 模型对S 盒的刻画:S 盒线性逼近表中的非零数值的绝对值为2、4 和8，因此在外MILP的基础上了另外添加两个分量(ε0，ε1) 来刻画S 盒的线性性质，对应关系如下:

因为内MILP 模型搜索的是高相关度的线性路径，由堆积引理，可转换为求指数之和的最小值，即

对所有的偏差非零的线性对，由离散点(x0，x1，x2，x3，y0，y1，y2，y3，ε0，ε1) 进行刻画，并将其作为集合Q4，记集合-Q4.最后，成功将不等式组的规模降至17 个(见表6)，并应用于PICO 算法内MILP 模型对S 盒线性性质的刻画.

4.2 PICO 算法最优线性区分器的搜索结果

基于上面对各组件线性性质的刻画，本文在PICO 算法差分区分器的两步MILP 搜索算法进行了部分修改，将各组件的差分性质的刻画替换为线性性质的刻画，完成了对PICO 算法线性区分器搜索.

在对模型的优化过程中，同样使用了减少变量和限制每轮活跃S 盒数目的方法.首先，将各轮的输入掩码表示S 盒的输入和输出掩码，这样可以减少大量变量数目.其次，在外MILP 模型中依然对轮函数中的活跃S 盒数目进行了约束，令其活跃S 盒数目不超过2 个，这样可以有效缩减搜索空间的可行域.除此之外，同样针对某一特定轮数，记该轮数下最小活跃S 盒数目为Mr，遍历搜索活跃S 盒数目[Mr，Mr+2]的所有线性路径，其中相关度最大的线性区分器为该轮数下的最优线性区分器.

对两步MILP 搜索算法进行改进，利用该算法，首次搜索到了3 条相关度为2-30的20 轮线性区分器，具体见表7(从左至右是从高比特位至低比特位)，这也是目前已知的PICO 算法轮数最长的线性区分器.与差分区分器的原理相同，该方法同样能以较大的概率搜到所有的最优线性区分器.

5 总结

本文基于MILP 模型对PICO 算法的差分分析和线性分析进行了评估.首先，对PICO 算法各组件的差分特征和线性逼近的传播规律进行精细刻画.其次，根据SPN 结构下置换操作的扩散规律以及S 盒特点，通过减少变量个数和限制轮函数中活跃S 盒的数目，缩小了搜索空间，优化了搜索策略，并建立了PICO 算法差分和线性区分器的搜索模型.最后，利用针对PICO 算法的两步MILP 搜索算法，找到了3条新的概率为2-63的21 轮最优差分区分器，并首次搜索到3 条相关度为2-30的20 轮最优线性区分器.这也进一步说明了: 在单密钥情形下，PICO 算法具有较好的抗差分和线性攻击能力.

另外，本文的工作也存在一些待解决的问题.对于找到的区分器，进行完整的差分和线性攻击是我们下一步的工作.另外，针对差分和线性路径的搜索方面，可以尝试用启发式方法对全局变量进行约束，简化其数学描述，将有助于进一步改进现有的密码分析结果.