基于K-shell的关键节点识别算法

王飞飞,孙泽军,赵 岩

(平顶山学院 信息工程学院,河南 平顶山 467036)

0 引 言

现实世界中的许多关系都可以采用复杂网络的形式表示,比如互联网、社交网络、物流网络、电力网络等[1].复杂网络中的关键节点是指与其他节点相比,对网络的结构和功能影响更大的节点[2-4].例如:在电力网络中,通过关键节点的识别可以对重要节点进行预测与控制[5-6];在病毒传播网络中,可以有效地判断出传播过程中的关键点,进行隔离与阻断[7];在社交网络中,可以加快良性信息的传播,阻断恶意信息的蔓延[8].因此,学者对于复杂网络关键节点识别的研究逐渐深入,许多关键节点识别算法被提出,比较典型的有CELF算法[9]、度折扣(Degree Discount)[10]、K-shell分解法[11]、度中心性(Degree Centrality,DC)[12]、接近中心性(Closeness Centrality,CC)[13]、介数中心性(Betweenness Centrality,BC)[14]、网页排名算法(PageRank,PR)[15]等.但是这些方法存在的共性问题为简单的算法结果不准确,影响力识别准确的算法过于复杂.因此,笔者提出了一种基于K-shell的关键节点识别算法(KNIK),该算法在计算节点影响力时,综合考虑节点自身影响力与其邻居节点能够为其提供的影响力,节点自身影响力基于节点自身的Ks值(Ks值根据K-shell算法获得)与度进行计算,邻居节点提供的影响力基于邻居节点的Ks值与度计算,同时引入邻居节点与该节点之间的关联性,该方法可以有效地对节点重要性进行识别.

1 相关工作

1.1 K-shell算法

K-shell算法对复杂网络中节点进行的是粗粒度划分,通过该算法计算每一个节点的Ks值,将节点分为若干层.具体思想为:首先,确定网络中度数为1的节点,删掉其连接的边,在剩余的节点中继续查找是否存在度为1的节点,如有则删掉其连边,直至网络中不存在度为1的节点,则该部分节点位于网络的第1层,其Ks值均为1;其次,确定网络中度为2的节点,删掉其连边,在剩余的节点中继续查找是否存在度小于等于2的节点,如有则删掉其连边,直至网络中没有度小于等于2的节点,该部分节点位于网络的第2层,其Ks值为2;最后,以此类推,循环执行上述过程直至确定每个节点的Ks值.

以图1为例进行说明,图1为无向无权网络图,包括14个节点,17条边.

图1 网络示例

通过K-shell算法计算图1中各节点的Ks值,其中,Ks值为3的节点有1、6、10、12,Ks值为2的节点有2、4,Ks值为1的节点有3、5、7、8、9、11、13、14.

通过K-shell算法将图1中的节点分为3层,Ks值相同的节点位于同一层,其重要性相同.该算法过于粗粒化,是对网络中节点位置的一种粗略划分,节点之间的区分度不大,有一定的局限性.

1.2 其他经典算法与近几年有代表性的算法

关键节点识别的经典算法中,度中心性判断关键节点最为简单直观,但是该算法仅考虑节点的局部信息,导致判断结果不够精确;接近中心性通过所有节点对之间的相对距离确定其影响力,虽然识别比较准确,但复杂度较高;介数中心性根据经过节点的最短路径数来确定节点的重要性,由于要对所有节点的路径数进行计算,复杂度较高;PageRank算法基于网页的链接结构对网页进行排序,但是其每个节点的跳转概率相同,且其中的参数需要实验获得,不具有普适性.与以上方法不同,CELF与度折扣算法基于贪婪算法进行改进,与传统贪婪算法相比,计算效率有所提高,但是准确度略微降低.

近几年来,在对已有算法研究的基础上,出现了许多算法,如ELKSS[16]、GIN[17]、RLGI[18]、MLI[19]等.在ELKSS算法中,基于KLSS提出了一种扩展局部K-shell和中心性的观点,但是该算法只考虑了节点的Ks值,具有一定的局限性.在GIN算法中,节点的重要性不但与自身有关,还与其连接节点的重要性相关,该算法较为简单,但是仅以自身与邻居节点的度、与邻居节点的距离作为影响因素,节点影响力识别的准确度不高.RLGI算法在形成前n个影响节点集的同时考虑其他节点的影响,该算法考虑了节点在网络中的位置,避免了重要节点聚集在某一范围内,但是该算法在计算时会降低强影响力节点邻近节点的影响力.MLI算法考虑到网络的拓扑信息,引入网络嵌入和机器学习,在识别动态传播下的关键节点方面效果较好,但是复杂度较高.

无论哪种算法,都以准确地识别节点影响力为目的,笔者在考虑运行结果准确性与算法复杂性的前提下,结合节点的局部与全局信息,提出了一种新的算法KNIK,该算法在节点Ks值的基础上引入了节点的度,同时引入节点与邻居节点之间的相似关系、邻居节点的Ks值与度,邻居节点贡献的加入可以使节点的检测更加有效;与其他算法相比,该算法简单,时间复杂度低,适用于较大规模的网络.

2 KNIK算法描述

2.1 算法设计

一个节点的影响力除了其自身,还会受到其邻居节点的影响,如果其邻居节点所处的位置越居于中心,影响力越强,则该节点的影响力也会越高,因此KNIK算法主要综合考虑节点自身的影响力与邻居节点对它的贡献.首先,计算节点的度与Ks值,根据节点自身的度与所在的层数计算节点自身初始影响力;然后,通过邻居节点的度、邻居节点所在的层与邻居节点与该节点的关联度来计算邻居节点为其提供的初始影响力;最后,综合节点自身初始影响力与邻居节点初始影响力,计算节点在网络中的影响力.

给定网络G=(V,E)为无向无权网络,V为网络中的节点集合,E为网络中的边的集合.

1)计算节点的度与Ks值.在网络G=(V,E)中,节点vi的度为D(vi),求其中所有节点度的最大值kmax与最小值kmin:

kmax=max(D(vi)),

(1)

kmin=min(D(vi)).

(2)

通过K-shell算法计算所有节点的Ks值,节点vi的Ks值为Ks(vi),求其中所有节点Ks值的最大值Ksmax与最小值Ksmin:

Ksmax=max(Ks(vi)),

(3)

Ksmin=min(Ks(vi)).

(4)

2)计算节点自身与邻居节点的初始影响力.节点vi的自身初始影响力为S(vi),根据节点vi的度、网络中节点度的最大值、节点vi的Ks值与网络中节点Ks值的最大值计算,由于节点的Ks值仅能粗粒化地反映节点的影响力,但是区分度不够,因此引入节点的度,两个因素共同作用可以一定程度上区分同一层节点的影响力,同时由于节点的度与Ks值不在同一计数层面,对其进行处理.计算公式如下:

S(vi)=D(vi)/kmax+Ks(vi)/Ksmax.

(5)

节点vi的邻居节点vj的初始影响力为N(vj),在计算邻居节点初始影响力时,由于不同位置的邻居对节点vi的影响不同,因此根据Ks(vi)与Ks(vj)的比较结果,将邻居节点分为3类,vj与vi在同一层,vj的层数小于vi,vj的层数大于vi,同时引入节点vi与邻居节点vj的关联度:

(6)

式中,vi的邻节点集合为Ω(vi),vj的邻节点集合为Ω(vj).

当Ks(vj)小于Ks(vi)时,弱化vj对于节点vi的影响力:

N(vj)=simj(vi,vj)(D(vj)/(kmax+
kmin))+Ks(vj)/(Ksmax+Ksmin).

(7)

当Ks(vj)与Ks(vi)相等时,

N(vj)=simj(vi,vj)(D(vj)/Ksmax)+
Ks(vj)/Ksmax.

(8)

当Ks(vj)大于Ks(vi)时,增强vj对于节点vi的影响力:

N(vj)=simj(vi,vj)(D(vj)/(Ksmax-kmin))+
Ks(vj)/(Ksmax-Ksmin).

(9)

3)计算节点vi在网络中的影响力.

(10)

式中,ns为网络中的节点总数.

该算法的详细过程如下所示:

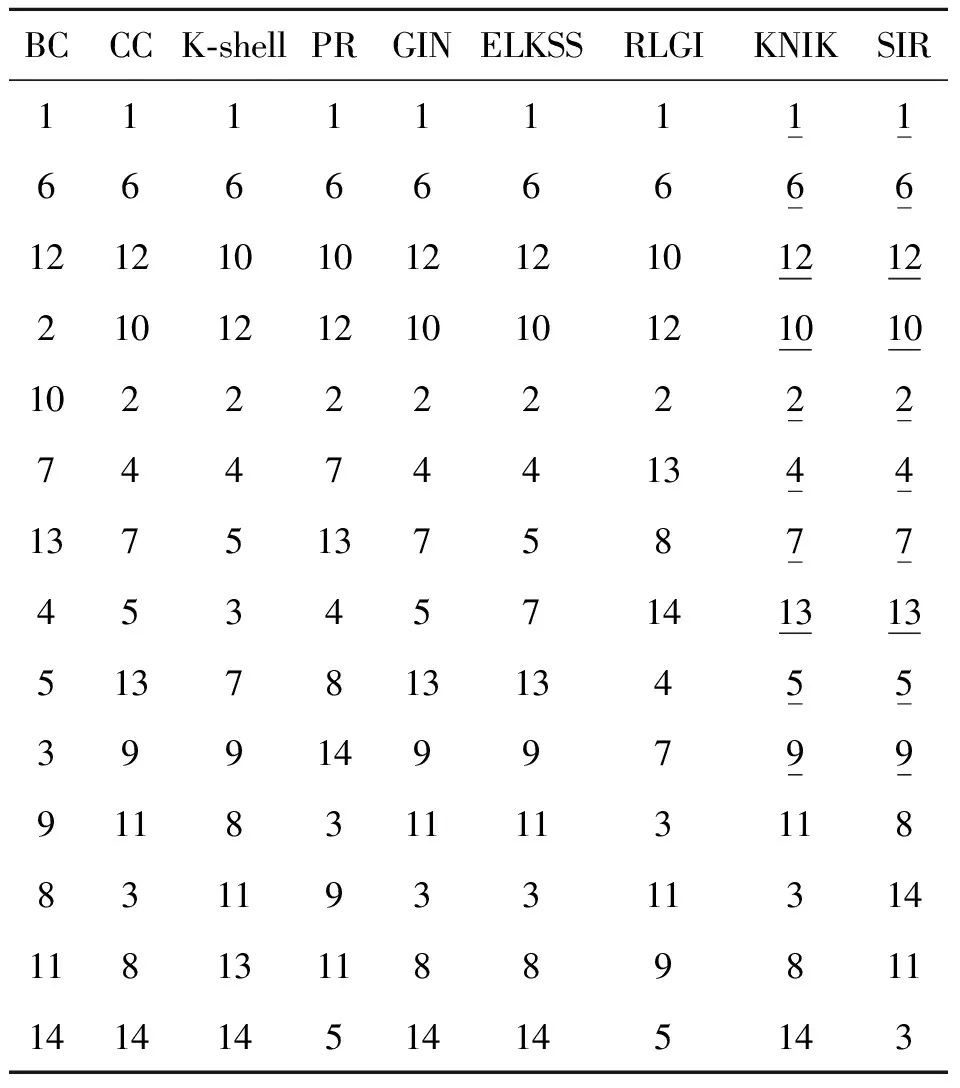
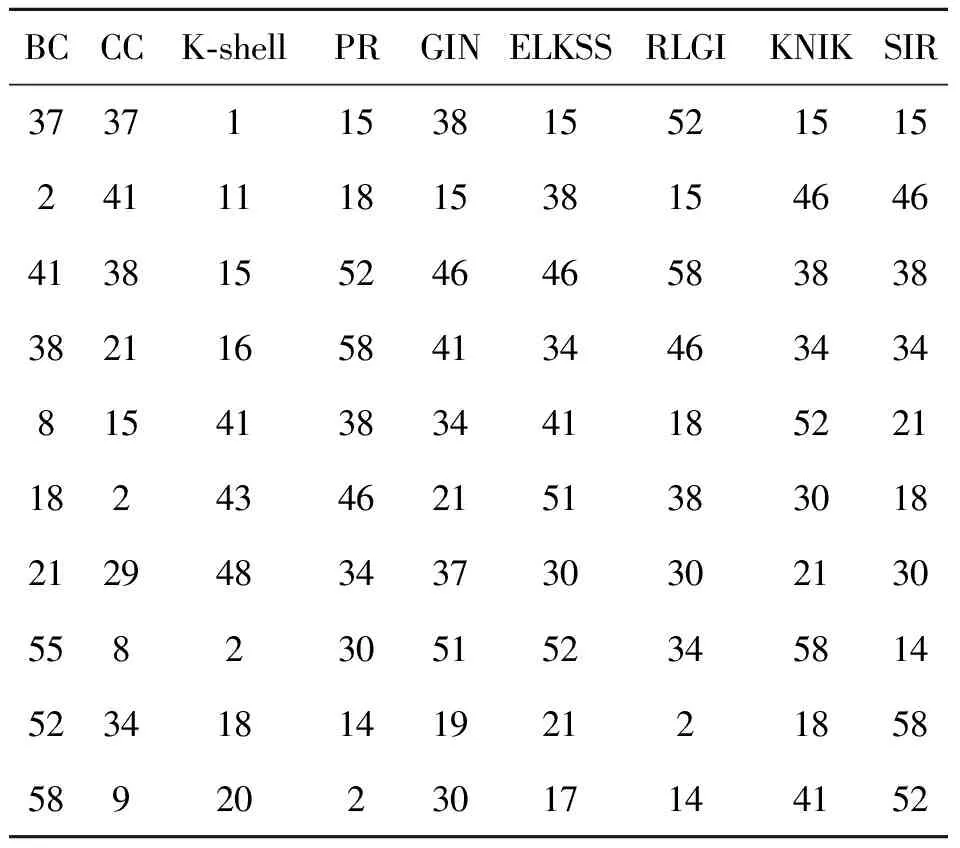
输入:G=(V,E)输出:所有节点的影响力值排序计算所有节点的度值,度的最大值与最小值计算所有节点的Ks值,最大Ks值与最小Ks值for 集合V中的每一个节点vi do 采用式(5)计算节点vi的初始影响力S(vi) for节点vi的邻居节点集中的节点vj do 采用式(6)计算节点vi与vj的关联度 if Ks(vj)

2.2 实例分析

为了对KNIK的算法过程进行描述,以图1中的节点v2为例:D(v2)=3,Ks(v2)=2;v2有3个邻居节点,分别为v1、v3、v4,D(v1)=6,Ks(v1)=3,D(v3)=1,Ks(v3)=1,D(v4)=2,Ks(v4)=2;在该网络中,kmax=6,kmin=1,Ksmax=3,Ksmin=1.

根据式(5)计算节点v2自身的初始影响力S(v2)=1.167;根据式(7)、(8)、(9)计算v2的邻居节点为其提供的初始影响力:N(v3)=0.321,N(v4)=0.917,N(v1)=1.95;根据式(10)计算节点v2在网络中的最终影响力,K(v2)=1.394.根据该方法可以计算出网络中所有节点的影响力.

将KNIK算法与各比较算法、SIR模型在Python中编程实现运行,得到网络中每个节点的影响力值之后进行排序,表1为排序后的结果.SIR模型中节点的感染概率设置为0.03.

表1 各算法在图1网络中的排序结果

由表1可知,KNIK算法的前10个节点与SIR模型一致,节点影响力识别较为准确.

3 实验评估

在本实验中,选用6个有代表性的真实网络,将KNIK与BC、CC、K-shell、PR、GIN、ELKSS、RLGI等7种算法进行比较分析,所有实验在台式计算机上运行,操作系统为Win10,CPU为 i7-9700,内存为16 GB.

3.1 数据集说明

6个网络为空手道网络、宽吻海豚网络、电子邮件网络、欧洲公路网络、美国航空网络与电网网络.

空手道网络(Karate network):该网络是美国一所大学的一个空手道俱乐部成员组成的网络.

宽吻海豚网络(Dolphins network):该网络是根据新西兰62只宽吻海豚的交往构造的社会网络.

电子邮件网络(Email network):西班牙一所大学的电子邮件通信网络,节点代表用户,节点之间的边表示用户之间存在电子邮件往来.

欧洲公路网络(Euroroad network):一个主要位于欧洲的道路网,节点表示城市,节点之间的边表示它们通过E-road连接.

美国航空网络(USAir network):该网络由美国联邦航空管理局国家飞行数据中心首选航线数据库构建.

电网网络(Powergrid network):该网络包含美国西部各州电网信息,节点是发电机、变电站或变压器,节点之间的边是用于供电的线路.

以上6个真实网络的相关特性统计信息如表2所示.

表2 6个真实网络的特性统计

在表2中,|V|为节点数,|E|为边数,为平均度,kmax为最大度,为平均聚类系数.

3.2 评价指标

3.2.1 SIR传播模型

SIR传播模型[20]是一个经典的关键节点识别的评价标准.过去十几年中,虽然已经提出了多种评价方法,但SIR模型仍然是最为广泛使用的节点影响力评估指标之一.因此,笔者采用SIR传播模型来对各种算法在不同网络上的运行结果排序进行比较分析.

在SIR传播模型中,根据节点状态不同将其分为3类:易感染节点S(Susceptible)、感染节点I(Infective)与恢复节点R(Recovered).网络初始化时,随机选择若干节点作为感染者I,其他节点则为易感节点S,每一个时间步内,I以一定的感染概率α感染与其相连的S类节点使其成为I类节点,同时已感染的I类节点以一定的治愈概率β进行恢复.此过程执行多次直至网络中不存在感染节点I,然后按照最终的感染节点数量获得所有节点的感染影响力排序结果.

3.2.2 Kendallτ系数

Kendallτ系数[21]用来衡量2个元素个数相同的排序列表之间的相似性.假设某算法的结果序列用X=(x1,x2,…,xn)表示,SIR模型的仿真结果序列用Y=(y1,y2,…,yn)表示.如果X、Y中的序列对(xi,yi)(i=1,2,…,n)同时满足xi>xj且yi>yj,或者xixj且yiyj,则认为这两个序列是不一致的;否则,认为既不是一致,也不是不一致.计算公式如下:

(11)

式中,n表示序列中的元素个数,nc与nd表示两个序列中一致与不一致的数量.τ值越大,则相似性越大,算法生成的排序结果越准确.

3.3 实验性能分析

3.3.1 不同数据集上前10个重要节点

为了对算法的性能进行分析,笔者将感染概率设置为0.03,恢复概率设置为1,通过实验获得SIR在不同网络中的执行结果.将各种算法在6个网络上运行获得节点影响力值,并将结果按降序排列.由于空间有限,此处只显示Dolphins与USAir网络的前10个节点.

表3是Dolphins网络前10个节点排序,KNIK算法与SIR模型获取的节点序列中有9个节点相同,其中前4个节点完全一致.

表3 Dolphins网络前10个节点排序

表4是USAir网络的前10个节点排序,KNIK算法与SIR模型的前8个节点相同.

表4 USAir网络前10个节点排序

3.3.2 不同感染概率下的肯德尔值

在该实验中,感染概率的取值范围为[0.01,0.1],SIR模型的模拟迭代次数设置为1 000.

图2为6个网络中8种算法获取的节点序列与不同感染概率下SIR模型获取的节点序列根据式(11)计算得到的Kendallτ值.

图2 Kendall τ值

由图2可知:KNIK算法在6个网络中整体效果较好,其中Euroroad与Powergrid网络在所有感染概率下Kendallτ值均大于其他算法,效果最好;在Karate与Email网络中,在少数感染概率下,Kendallτ值低于算法GIN与ELKSS;在Dolphins与USAir网络中,在少数感染概率下,Kendallτ值仅低于算法ELKSS,但是在其他感染概率下,KNIK的效果仍为最好.因为KNIK算法不仅考虑了节点在网络中的位置,同时引入了节点的度与邻居节点能够为其提供的影响力,提高了节点影响力值计算的准确性.

3.3.3 8种算法在SIR模型上的传播能力值比较

笔者将SIR模型中的节点感染概率设置为0.03,恢复概率设置为1.将8种算法在6个网络上运行取得的结果序列与SIR获得的结果序列进行比较,获取各节点在SIR模型中的感染能力,节点的重要性与其感染能力成正比.如果算法效果较好,结果序列与SIR模型结果序列较为一致,则曲线自左至右呈平滑下降趋势,否则呈不规则的折线.

在图3中,根据网络节点多少采用不同的显示形式,Karate、Dolphins两个网络节点数较少,数据以线性形式显示,其余网络节点数较多,数据采用取常用对数的形式,该方式可以将影响力较大的节点进行侧重显示.由图3可知,在Karate、Dolphins与Euroroad网络中,KNIK算法的曲线基本呈下降趋势,表明该算法效果优于其他算法;在USAir与Powergrid网络中,虽然KNIK算法曲线存在跳跃,但是整体效果仍优于其他算法;在Email网络中,KNIK算法与ELKSS效果相似,但是优于其他算法.因此,在所有网络中,KNIK算法整体效果较好.

图3 8种算法在6个网络中的节点感染能力

4 结 论

笔者在对现有关键节点识别算法进行研究的基础上,提出了一种基于K-shell的关键节点识别算法,该算法结合节点的局部与全局信息,根据节点度与Ks值、邻居节点的度与Ks值,同时引入节点与邻居节点之间的关联度计算节点的影响力,该算法解决了K-shell算法区分节点粗粒化的问题,提高了节点影响力识别的准确性.为了对算法效果进行验证,以SIR模型为参照,以Kendallτ值与节点在SIR模型中的感染能力为评价标准,与其余7种算法在6个网络上进行实验.实验结果表明,该算法能够较为准确地识别网络中的关键节点,整体效果较好.