基于Grasshopper 的参数化方法在车辆等效均布活荷载计算中的应用

王昕 李保忠 汪光满 胡达敏

（浙江绿城建筑设计有限公司，杭州 310007）

引言

建筑物全生命周期中，车辆荷载是不可避免的临时和使用活荷载之一，包括建造、改建和拆除过程中的各种类型和规格的工程车辆和使用过程中的各类车辆如中大型客车、货车及消防车辆等。对于大型消防车辆、货车和汽车吊等吨位较大的车辆，在结构设计或复核时，需要对其荷载作用进行恰当的考虑。

由于车辆对楼盖的实际作用情况较为复杂，工程设计中常通过均布于结构楼盖的车辆等效均布活荷载（以下简称车辆等效荷载）来考虑车辆作用，等效荷载的合理取值是结构设计安全和经济的重要前提，本文提出了一种参数化的车辆等效荷载计算模型，用于计算不同车辆作用于不同楼盖结构的等效荷载。

1 车辆等效荷载研究现状

车辆活荷载实际上通过各车轴的轮压形式作用于结构楼盖上，对部分吊车和消防登高车，在工作过程中还将通过附带的撑脚支撑于结构之上。如果结构楼盖上部存在覆土，轮压或撑脚压强将在覆土中进行扩散。

现行荷载规范[1]中，根据轮压的最不利布置，给出了车辆等效荷载的构件效应等效计算原则，即等效荷载和实际车辆荷载作用下结构构件的最不利效应相等，以此计算得到车辆的等效荷载，并给出了一些常见规格车辆的等效荷载设计取值。除规范以外，许多文献也对工程中最常见的消防车等效荷载进行了研究[2-5]。

但在实际工程设计中，对于车辆等效荷载，规范和已有研究还存在以下不足：

（1）工程中常遇见荷载规范中和文献研究中未能涵盖的车辆规格。荷载规范中仅给出了少数车辆的等效荷载，许多规格车辆尤其是大吨位车辆无法直接根据规范取值，也缺乏研究其等效荷载的文献可供参考；

（2）除车辆外，车辆作用的楼盖结构形式和柱跨、构件尺寸、覆土厚度等结构参数同样对车辆等效荷载存在重要影响，规范和已有研究尚未完全覆盖众多的楼盖结构形式和参数；

（3）根据构件效应等效原则计算车辆等效荷载时，其最不利轮压分布位置通常无法简单确定，尤其涉及到多辆车辆或大型车辆车轴数量较多时，对于不同构件如何确定最不利的车辆位置，传统有限元软件的求解流程较为繁琐，需要通过反复修改轮压分布位置进行大量试算。

2 车辆等效荷载参数化计算模型

从上述车辆等效荷载研究现状可以发现，车辆等效荷载问题包含了车辆和结构两方面要素的众多参数，因而针对少数特定参数的分析结果难以覆盖众多的实际工程情况。将车辆和楼盖结构通过一定逻辑分解为若干基本参数，建立参数化的车辆等效荷载结构计算模型，可以有效解决这一问题。通过调节车辆和楼盖结构的参数，就可以实时生成不同车辆和楼盖结构的等效荷载参数化计算模型和等效荷载计算结果。

常用结构参数化平台可分为两大类：一类是基于通用有限元软件平台，并结合有限元软件提供的参数化功能，如ANSYS 软件结合APDL 参数化语言[2,4]、SAP2000 软件结合API 二次开发功能等，其特点是有限元分析功能强大，但参数化功能通常依赖于软件底层语言或二次开发，对于工程师不够直观高效；另一类是基于三维建模软件平台及软件自带的参数化建模模块，如Rhino 软件和Grasshopper 参数化模块[6-9]，通常此类软件的参数化建模功能强大且直观，但不足之处在于结构分析功能的缺失，需要借助第三方插件或二次开发加以实现。另外，也有通过二次开发将参数化三维建模软件和结构有限元分析软件连接起来的做法，使两类软件各取所长，前者负责参数化建模，后者负责结构分析。但这种做法对使用者的二次开发能力要求较高，同时调用有限元软件通常系统开销较大，影响模型求解速度，难以做到从基本参数到计算结果的实时联动，数据在不同软件之间流体也存在较多限制。

本文采取的方法是基于Rhino+Grasshopper 参数化平台，同时借助第三方有限元插件Karamba3D，并在有限元计算结果的基础上进行了二次开发，构件了参数化的车辆等效荷载计算模型，可以根据实际工程情况，直接车辆和楼盖结构参数，实时获得动态的车辆等效荷载计算结果。上述方法的主要流程简述如下：

（1）将不同类型的车辆统一为车身尺寸、车轴数量、轴重、轴距、轮压面积等基本参数，通过调整参数即可快速建立车辆荷载作用模型；进一步通过定义车辆数量和间距参数，实现任意行列数量的车辆布置；楼盖上存在覆土时，通过覆土厚度和轮压扩散角参数，进一步将车辆直接轮压转换为通过覆土扩散后的作用于结构的扩散轮压；

（2）楼盖结构同样可统一为结构形式、柱跨、构件尺寸、材料参数、边界条件等基本参数，通过一定逻辑建立参数可调的动态楼盖有限元模型；

（3）通过车辆位置参数，即可将车辆轮压施加于楼盖模型的指定位置，进行结构有限元计算后获取弯矩和剪力等构件效应；

（4）可将楼盖指定区域所有构件的效应与均布单位荷载下的效应进行对比，根据构件效应等效原则计算车辆等效荷载；

（5）改变任意车辆或楼盖结构参数，即可实时更新车辆等效荷载；

（6）可进一步定义车辆开行路线，将车辆开行范围离散为一系列车辆坐标点，计算所有坐标点的车辆等效荷载，获得车辆的最不利位置和由此产生的等效荷载包络值。

3 主要模块

根据上述求解流程，本文参数化车辆等效荷载结构计算模型可分为车辆模块、楼盖模块、等效荷载计算模块和车辆开行模型四个主要模块。

3.1 车辆模块

3.1.1 单车规格

不同类型车辆可统一通过以下参数定义：车辆尺寸、车轴数量、轴距、轴重、各轴轮压接触面积以及用于确定车辆在楼盖上位置的车辆坐标原点，此坐标原点可自行约定保持各模块一致即可，本文模型中以车辆最前排车轴中点作为车辆坐标原点。以30 吨消防车为例，其基本参数如表1 和图1 所示。

图1 30 吨消防车整车尺寸和轮压着地尺寸(mm)

表1 30 吨消防车参数表

3.1.2 单车轮压

定义车辆参数后，若存在覆土，则根据行车路线的覆土厚度和轮压扩散角参数，即可获取每个车轮的轮压施加范围和轮压压强大小。30t 消防车单车轮压生产运算器如图2 所示。

图2 生成单车轮压运算器（以30 吨消防车为例）

3.1.3 多车排布

计算车辆等效荷载时，有时候需要考虑多车辆同时开行的情况。比如，多辆消防车同时参与火灾施救，此时需要补充定义车辆数量，车辆前后、左右间距等参数。同时，此时用于确定车辆在楼盖上位置的参数由原来的单车坐标原点变为车群坐标原点。图3 为从单车轮压生产多车轮压的运算器图示，图4 为4 辆30t消防车2x2 排列时的轮压分布示意。此轮压用于施加于楼盖结构模型并计算车辆等效荷载。

图3 从单车轮压生成多车轮压并重置原点坐标

图4 车辆参数生成单车轮压再生成多车轮压示意图

3.2 楼盖模块

3.2.1 楼盖参数

楼盖参数主要包含楼盖结构形式、楼盖跨数、各主跨跨度、构件截面尺寸，构件材料参数，边界条件，网格划分参数等，用于建立楼盖结构的有限元模型。工程中常见的楼盖结构形式包括主梁+大板、主次梁体系、无梁楼盖等，其中，主次梁体系又可分为井字梁、十字梁、单向双次梁等，不同楼盖类型包含不同参数。因此，楼盖结构形式是需要首先确定的参数。确定了楼盖结构形式，并补充其他楼盖参数后，即可通过上述参数建立楼盖有限元模型。

3.2.2 楼盖建模

参数定义完成后，楼盖有限元模型的生成借助Grasshopper 下的Karamba3D[10]有限元计算插件。Karamba3D 可将Grasshopper 生成的线和面实体转换为有限元框架单元和壳单元，并通过额外定义的材料、约束、荷载等进行有限元计算，获取单元内力，经过与CSI 的SAP2000 软件的比较，两者计算结果接近，精度满足要求。相比常见的有限元软件，Karamba3D 的优势在于将有限元分析功能整合进了Grasshopper 中，可以与Grasshopper 实时联动，修改Grasshopper 中的任意参数时，Karamba3D 将实时更新计算结果，使得工程师能够非常直观的观察各个参数对计算结果的影响。楼盖中梁采用框架单元模拟，楼板和柱帽采用同时考虑面内和面外刚度的壳单元模拟，模型根据网格划分参数对各跨梁板进行网格划分，默认的划分数量为梁划分为15 段，楼板划分为15x15 个网格，梁和楼板在共同节点处实现协同变形。模型对所有支座节点约束全部6 个自由度，以模拟柱子对梁的约束。

以主梁+大板楼盖为例，表2 为楼盖主要参数，图5 为通过表中参数生成楼盖有限元模型的运算器示意图，除楼盖自身参数外，还引入了车辆模块生成的轮压作为荷载施加于模型上。图6 为生成的楼盖有限元模型示意图。

图5 生成楼盖计算模型运算器

图6 Karamba3D 楼盖有限元模型

表2 楼盖主要参数

3.3 等效荷载计算模块

通过参数化楼盖有限元模型，可以计算获取构件的内力，楼盖构件效应主要指梁的弯矩剪力及楼板弯矩。此时即可通过构件效应等效的原则，计算构件的车辆等效荷载。根据荷载规范，车辆等效荷载为与实际轮压作用下最不利构件效应相等的均布荷载。

3.3.1 构件效应计算

为了计算车辆的等效均布活荷载，需要获取两种工况下的楼盖构件效应，分别为实际的车辆轮压作用工况和用于计算等效荷载的满布单位均布荷载工况。

不同构件用于计算等效荷载的最不利构件效应也有所区分。对于楼板，最不利构件效应包含最大正弯矩和最大负弯矩。值得注意的是，在移动车辆轮压的作用下，楼板的最大正弯矩并不一定位于板跨跨中，需要准确获取楼板的最大正弯矩而非跨中弯矩。对于梁，最不利构件效应包含最大正弯矩、最大负弯矩和最大剪力，同样的，梁最大正弯矩不一定位于跨中。

楼盖有限元模型求解完成后，可通过运算器获取各构件的弯矩和剪力效应，并求得用于计算等效荷载的最大弯矩和剪力。

3.3.2 等效荷载计算

等效荷载的取值即为构件在实际轮压作用下各最不利构件效应与单位均布荷载下对应值比值的最大值，以楼板为例，其等效荷载计算结果取以下两者的较大值：（a）轮压作用下各楼板最大正弯矩与均布单位荷载下最大正弯矩比值；（b）轮压作用下各楼板最大负弯矩与均布单位荷载下最大负弯矩比值。

梁等效荷载的计算结果则取以下实际轮压作用下最大正弯矩、最大负弯矩以及最大剪力与均布单位荷载作用下对应值比值的较大值。计算过程中可以发现，车辆轮压位置不同时，梁等效荷载有时由剪力控制，有时由弯矩控制。

3.4 车辆开行模块

上述等效荷载的计算均基于静态的轮压分布，实际车辆开行时，车辆位置不同，轮压分布发生变化，构件等效荷载也将对应变化。显然，等效荷载的计算需要首先确定车辆的最不利作用位置，所谓最不利作用位置，指车辆在此位置时，梁或板将产生最大的构件效应并对应最大的等效荷载。

当车轴或车辆数量较多时，面对复杂的轮压分布，通常难以直接确定车辆在楼盖上的最不利作用位置；其次，对于梁和楼板而言，最不利作用位置并不相同。

而借助参数化工具，不需要事先确定车辆最不利作用位置，可以通过不断调整车辆位置，比较车辆在各位置的等效荷载计算结果来确定最不利作用位置，并获取对应的最不利等效荷载。

此过程可借助Anemone 插件自动化，Anemone 可以在Grasshopper下实现类似编程语言的循环函数功能。

当车辆开行路线确定时，可将开行路线离散为n个车辆坐标点；而当车辆没有确定的开行路线仅有大致的开行范围时，可将开行范围离散为n×m个坐标点；此后即可对所有的坐标点进行遍历计算，用于确定最不利轮压的车辆坐标及对应等效荷载。

对X 方向定义行车路径上的n 个计算点，对Y 方向定义行车路径上的m 个计算点，则共有n x m 个位置需要计算车辆等效荷载，可生成车辆坐标点阵，进行所有坐标点的遍历计算，用于确定最不利轮压的车辆坐标及对应等效荷载。

图7为实现n×m个车辆位置遍历计算的运算器图示。

图7 实现n ×m 个车辆位置自动遍历计算运算器图示

4 算例

车辆等效荷载参数化计算模型算例如下：以四梁30 吨消防车作用于结构类型为主梁+大板的楼盖为例，柱跨尺寸两个方向均为9m，梁宽400mm，梁高900mm，板厚300mm，覆土厚度1.5m，覆土扩散角取35°；30 吨消防车车辆参数同表1，四辆消防车两前两后排列，开行时维持前后车距0.5m，左右车距0.5m。图8 中黑点代表离散化的消防车开行范围内车队坐标原点点阵，开行范围内梁和楼板等效荷载计算结果，以及梁板等效荷载比值（即荷载规范中的梁等效荷载折减系数）如图9（a）～（c）所示。

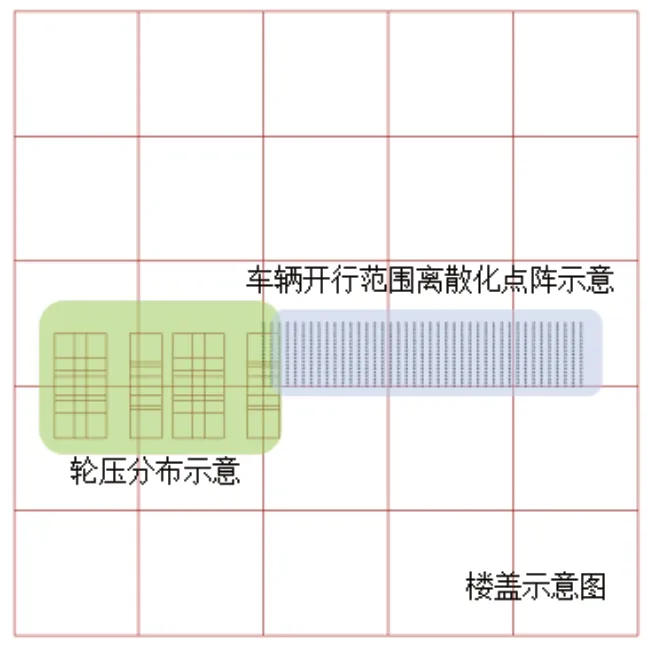
图8 车辆等效荷载参数化计算模型示意图

图9 车辆开行范围内各位置梁板等效荷载计算结果

可见，参数化计算模型可以得到车辆开行范围内，基于构件效应等效原则的最不利位置的车辆等效荷载。此时，也可以根据各构件在车辆开行过程中的最不利弯矩和剪力，直接对构件进行设计或复核。

5 结论

本文根据车辆等效均布活荷载计算的特点，提出了基于Rhino+Grasshopper 的参数化计算方法，并介绍了其具体建模和计算步骤以及参数化方法的优势，结论如下：

（1）Grasshopper 参数化建模结合Karamba3D 有限元分析，在单一Rhino 软件平台下即可实现结构参数化模型，是基于参数化的结构分析和设计有效方法；

（2） 借 助Rhino+Grasshopper 平 台， 利 用Grasshopper 参数化建模的特点，并通过第三方有限元插件Karamba3D 和二次开发，建立了参数化车辆等效荷载计算模型，可调整车辆和结构参数并实时得到等效荷载计算结果；

（3）借助Anemone 插件可实现自动求解车辆开行范围内所有位置的等效荷载，从而获得车辆对结构作用的最不利位置和对应的等效荷载最大值。