基于EMD-SVD的高压电缆局部放电信号降噪算法研究

张小牛，景俊伟，林 健，张 哲，马星河

（1.平顶山天安煤业股份有限公司，河南平顶山 467000；2.河南天通电力有限公司，河南 平顶山 467000；3.河南理工大学，河南 焦作 454000）

高压电缆现场存在着大量复杂的噪音信号，当噪音信号较大时，影响检测的PD 信号[1-2]，因此需对现场采集的信号进行降噪。目前的解决方法有傅里叶变换[3]、小波变换[4]、经验模态分解（EMD）[5-7]等。傅里叶变换可处理线性和稳态信号，但PD 信号是非平稳信号。小波变换虽然可以有效地抑制白噪音，但其基函数是固定的。

经验模态分解能将非线性、非平稳态信号分解成若干个线性、稳定的模态函数,通过排列熵筛选出含噪特征信号，再采用奇异值分解，通过熵增量定阶理论将高频噪音分量对应的奇异值归为零，通过逆过程对信号进行重建，就得到降噪的PD 信号。

1 算法原理与步骤

1.1 经验模态分解

任一信号通过EMD 分解为若干个模态函数IMF之和，每个模态函数IMF 必须满足以下条件[8-9]：

1）在整个信号中，极值点与过零点的数量差≤1。

2）局部最大值与最小值的均值为0。而实际工程中，均值的绝对值小于某个很小的数即可。

EMD 算法步骤如下：

在确定原信号x(t)的极值点之后,利用三次样条函数准确得出上包络线e+(t)与下包络线e-(t)，其上、下包络线的平均包络为m1(t)，则：

原始信号与m1(t)相减，得到去掉低频后的信号hk(t),即：

h1(t)一般不是一个稳定的信号，因此IMF 的两个定义条件都不满足，那么就必须反复进行以上步骤，直到获得满足IMF 定义的信号hk(t)为止,也就是一阶IMF 分量：

原信号x(t)减c1(t)得到去掉高频的新信号r1(t)：

通过对原始数据反复执行以上的步骤，r1(t)可以得到第二个分量c2(t)，且该第二个分量c2(t)符合IMF 的条件，然后重复执行，直至得到n阶IMF 分量cn(t)或者当rn(t)变成单调函数或者符合IMF 条件的分量不能被常量所提出时循环就结束了。此时，通过EMD 分解x(t)获得：

此时可以得到n个频率从高到低的本征模态函数IMF 以及一个残余量rn(t)。

根据EMD 算法步骤，可得流程图如图1 所示，其中SD 为给定门限，这里取0.1。

1.2 SVD分解去噪

假设信号X(N)={x1,x2,x3,…,xn}为原始含噪音信号，对其构建m×n阶Hankel矩阵[10-11]如下：

工程应用中一般取m=N/2[9],n=N-m+1。

H矩阵经过奇异值分解可得到：

U和V分别为m×m与n×n矩阵，S=diag(λ1,λ2,…,λk)，其中，λk为矩阵H的奇异值，且λ1≥λ2≥…≥λk≥0，k=min(m,n)。有用信号可以通过前a个较大的奇异值来反映，其余的则反应噪音信号，无用的奇异值取零，当通过对奇异值分解的计算过程为逆过程时，对有用信号进行筛选，并对其进行重组，即可获得噪声减小后的信号，如下：

其中，p=min(n,i)，q=max(1,i-m+1)。

2 EMD-SVD联合降噪

1）经过EMD 分解后，得到n个IMF 分量以及残余分量rn(t)。

2）模态分量可以分为纯噪音信号、含噪特征信号以及纯特征信号。通过计算每个模态的PE 值，将PE 值作为筛选模态分量IMF 的阈值，白噪音的排列熵在0.9 左右，含噪特征信号在0.6 左右，PE＜0.070 60时为低频基线漂移分量[12-13]。

3）首先，Hankel 矩阵是由利用滤波后的噪声特征信号建立的，将其分解为奇异熵，并绘出奇异熵的增量曲线求出奇异值的有效阶次，然后，置零无效奇异值筛选有用信号，通过对信号进行重建，可以获得噪音削弱之后的IMF 分量。

4）将上述降噪之后的IMF 分量与纯特征信号IMF分量进行重构，就可以得到降噪之后的PD信号。

3 仿真实验

根据文献[14-16]可知，局部放电信号存在四种衰减形式，分别为单、双指数衰减，单、双指数衰减震荡。该文选用单、双指数衰减震荡作为仿真信号，其数学表达式为：

①单指数衰减震荡如式（9）：

②双指数衰减震荡如式（10）：

在上述公式中，参数A表示脉冲强度，A1为0.22 mV，而A2为0.9 mV，τ表示为衰减常数，通常情况下取1 μs，fc表示1 MHz 的振荡频率，而其采样点数N为1 200 个，将具有1 dB 信号强度的白噪音添加到最初纯净的PD 信号（见图2），当PD 信号加白噪音之后，此时如图3 所示。

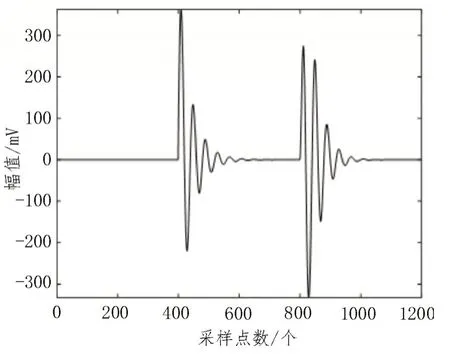
图2 纯净PD信号

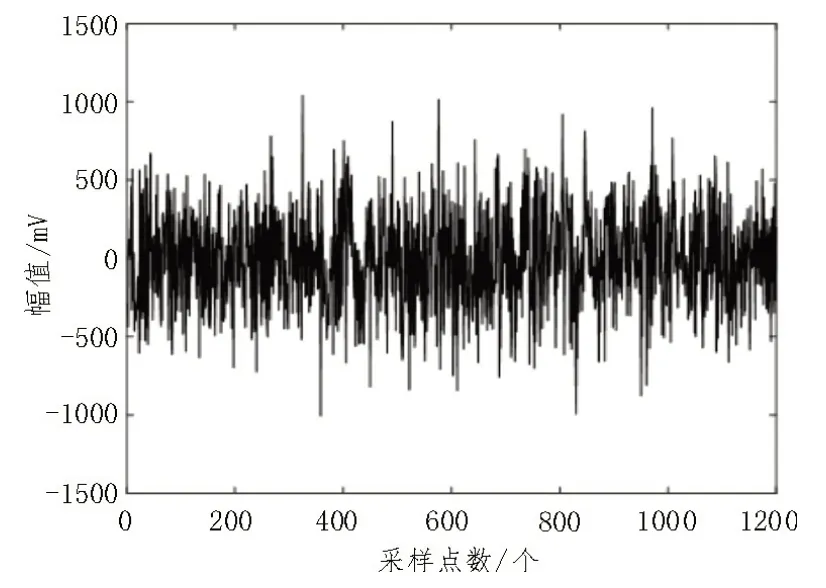
图3 加噪PD信号

由图3 可以明显看到，白噪音完全覆盖了PD 信号，如果不对其进行降噪处理，将不能用于实验分析。当利用EMD 分解PD 信号时，最终获得九个本征模态分量IMF，如图4 所示。

图4 模态分量IMF

然后计算每一模态分量的排列熵PE（如表1 所示）筛选IMF 分量进行下一步转换矩阵，一般白噪音的排列熵在0.9 左右，排列熵大于0.790 7 时为高频分量，所以IMF1 为噪音分量，故舍弃。IMF9 的PE＜0.070 60，为低频基线漂移分量，舍弃IMF9。0.6 左右的为间歇信号，因此对PE 值大于0.5 的模态分量进行降噪处理，即对IMF2 进行矩阵转换，再通过奇异值筛选有用信号，去除噪音信号，IMF3-IMF8 为特征信号。

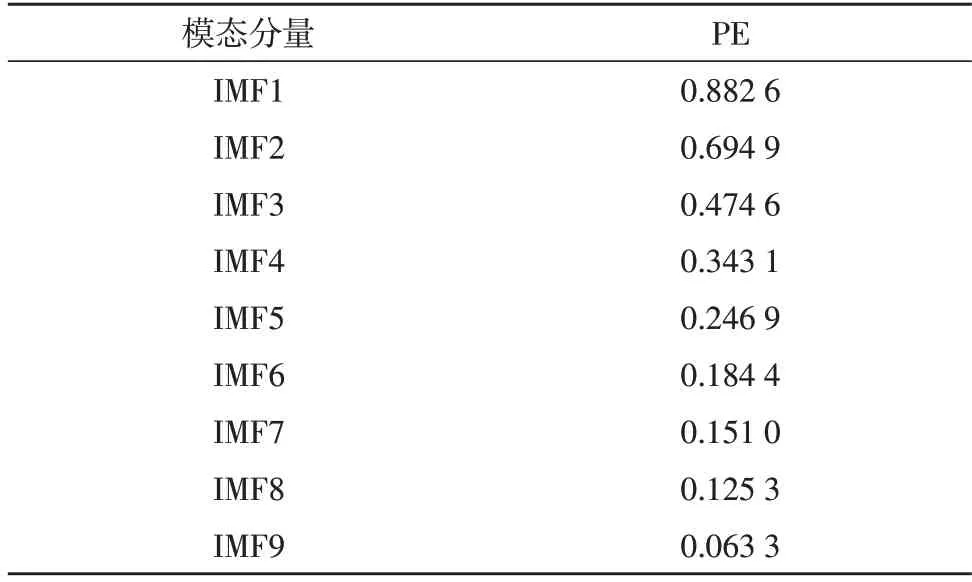
表1 各模态分量PE值

通过把IMF2 变成Hankel 矩阵,进而使得奇异值开始分解，从而获得了奇异值，其分布如图5 所示，通过奇异值曲线（如图6 所示局部放大图）确定有效阶次，当奇异值阶次大于13 时，奇异值的变化逐渐平稳，即奇异熵增量不再随着阶次的升高而明显降低，因此将阶次小于13 的奇异值置零，进行信号重构。

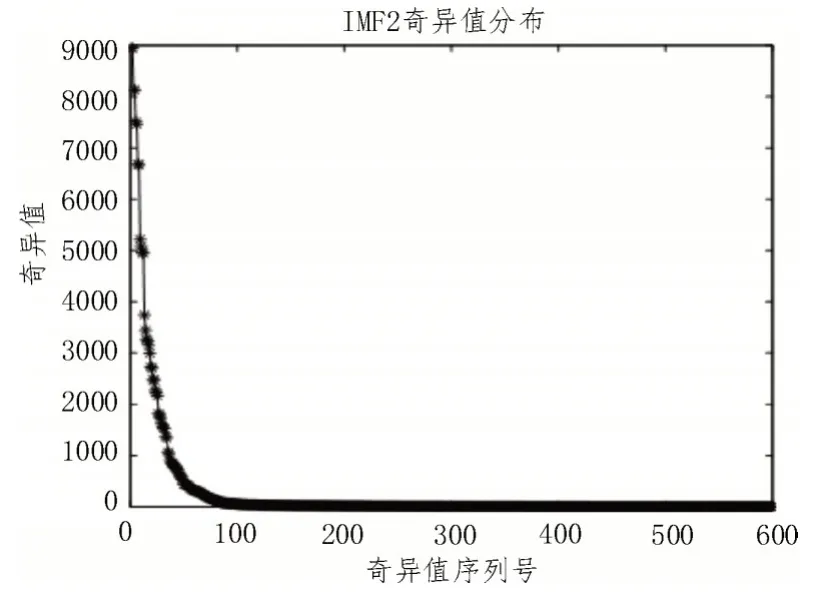
图5 奇异值分布

图6 局部奇异值放大图

通过SVD 重构得到降噪之后的IMF2 分量，并将之与IMF3-IMF8 重构局部放电信号（PD）。经EMDSVD 联合降噪处理后的PD 信号如图7 所示，降噪处理前后的对比图如图8 所示，以及仅仅通过EMD 分解PE 值筛选重构而未经奇异值筛选信号处理图如图9 所示。

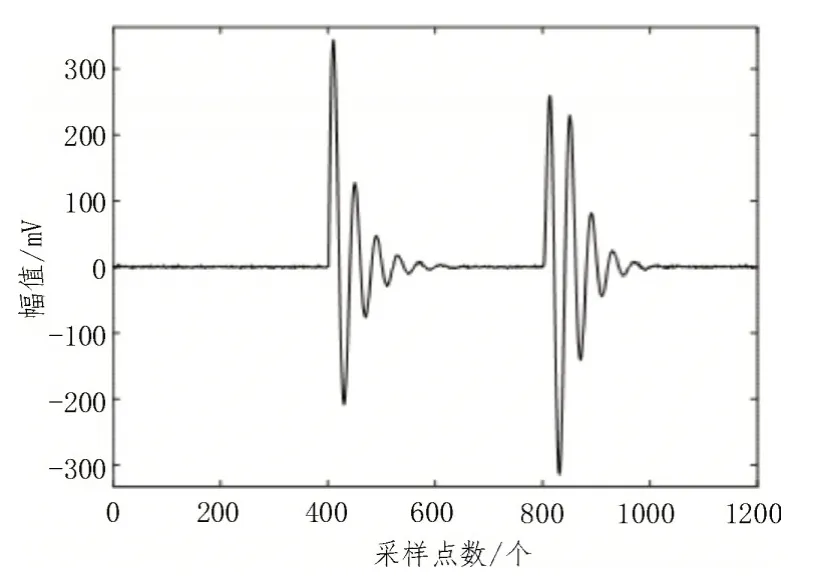
图7 EMD-SVD降噪处理后的信号

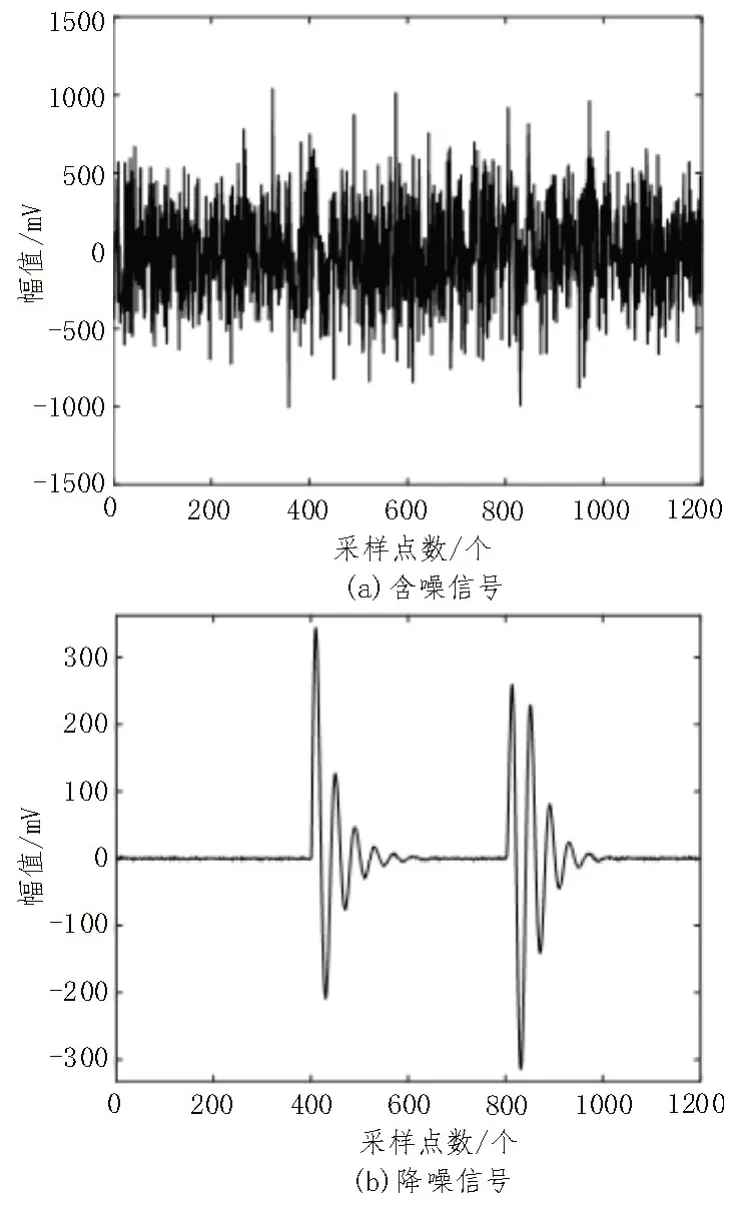
图8 降噪处理前的加噪与纯净PD信号

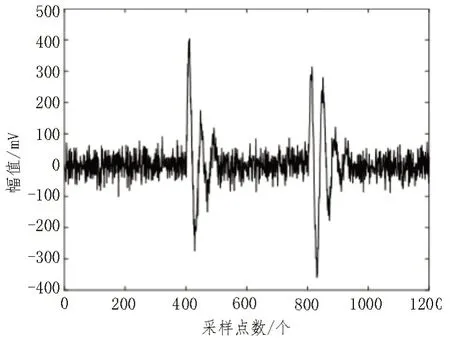
图9 PE值筛选降噪

通过图6-9 可以明显看到，EMD 分解之后通过PE 值筛选降噪处理，仅能产生略微的消噪作用，而EMD-SVD 联合降噪效果明显，处理之后的信号和正常原始纯净信号几乎无异。

为了验证该文方法在加速度信号在不同噪声情况下的噪音削弱的效果，通过援引信噪比(Signal to Noise Ratio，SNR)和均方误差(Mean Square Error,MSE)来测得此方法削弱噪音的效果，如表2 所示。

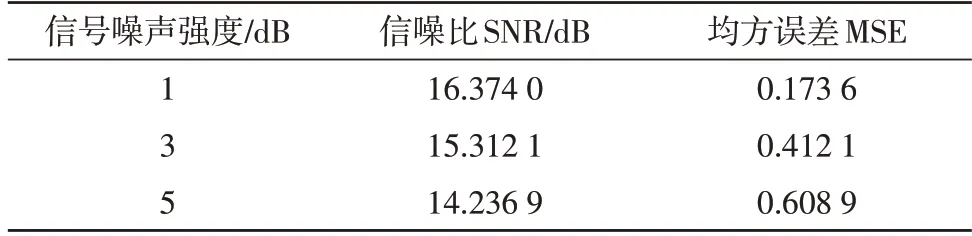
表2 不同信噪比环境下的去噪效果

4 结论

通过仿真结果可以知道，该文先对局部放电信号（PD）进行EMD 分解，再通过PE 值进行筛选含噪特征分量，用筛选出来的含噪特征分量构建Hankel矩阵，然后进行奇异值的分解过程，通过奇异值熵增曲线筛选有用信号，再次经滤波后重建噪声减小后的分量和特征信号分量,即可得到完整且特征明显的PD 信号。由此通过该文所提出的EMD-SVD 联合算法对高压电缆PD 信号具有良好的降噪效果。