汽轮机进汽阀组流量特性辨识方法

朱龙飞,陈晓峰,左 川,谢昌亚,张 腾,仇晓智

(1.国网冀北电力有限公司电力科学研究院,北京 100045;2.北京京能电力股份有限公司,北京 100025)

0 引言

现代大、中型火力发电厂机组中汽轮机均采用数字电液控制(DEH)系统进行控制。阀门管理是DEH系统的一项重要功能,但实现该功能需要获得准确的汽轮机阀门特性,若DEH系统中预置曲线与实际阀门流量特性曲线存在差异,则会因准确性不足而影响方案设计和机组安全运行。目前国内机组出现故障的原因之一便是使用的阀门流量特性曲线不符合实际情况,因此无论是从机组安全运行还是经济性考虑,都有必要计算出符合实际情况的阀门流量特性曲线。

切合机组实际情况的阀门流量特性曲线,可以使机组的单阀/顺序阀切换过程更平稳,负荷扰动更小,增强机组变负荷和一次调频的能力,提高机组运行的经济性和控制的稳定性[1-3]。李劲柏等[3]通过对流量变化过陡和过缓区段进行调整以及重新选择阀门重叠度的手段优化了阀门流量特性,使机组运行更加稳定。赵征等[4]进行了阀门特性实验,通过阀门特性曲线整定优化了机组负荷控制过程及自动发电量控制过程。李前敏等[5]对测得的流量特性曲线进行了修正,采用Savitzky-Golay算法进行数据处理,并利用最小二乘法优化算法对曲线进行了拟合。

目前获得汽轮机阀门流量特性曲线的方法为调节级变工况计算,但步骤极为繁琐,且通用性较弱。本文提出了一种简化建模方法,通过机组实际运行情况分析得到了影响进汽阀组通流特性的主要因素,指出了耦合效应的起因,将耦合效应简化为两个变量函数的乘积,并通过理论分析确定了函数结构,利用运行数据对函数进行了拟合,从而生成了接近实际情况的阀门流量特性曲线。

1 进汽阀组间耦合效应分析

汽轮机是大型热电厂中最常见的热力机械,其原理为高温高压蒸汽依次流经汽轮机各级叶片膨胀做功,从而带动转子发电,增大或减小进汽阀门的开度可以相应地增大或减少蒸汽流量,从而改变汽轮机出力,即汽轮机调节系统将功率增量转化为阀门控制信号增量(综合阀位指令),进一步变为流量增量。

这意味着汽轮机调节系统的正常运行严重依赖于综合阀位指令与流量之间的线性关系,然而,在机组实际运行中,机组流量与综合阀位指令之间往往无法呈现出良好的线性关系。

汽轮机阀门内部蒸汽流动情况十分复杂,首先,当阀门几何结构、尺寸不同时,内部蒸汽流场会有较大差异,在阀腔转折处易形成空腔、漩涡等;其次,当蒸汽温度、压力、流速不同时,蒸汽流动性质也会发生差异,如速度过快时易在转折处形成激波等流动状态发生剧变的界面,除此以外,蒸汽的粘性也会使改变阀内通流情况。

尽管影响阀内蒸汽流动特性的因素很多,但因存在主要与次要之分。如图1所示,汽轮机通过阀门组来控制流量。

图1 汽轮机阀门组示意图

阀组由4个阀门构成,有两种运行方式,一种是单阀运行,即四个阀门同开同闭,同步调整,但这种方式节流损失较大,因此常用另一种运行方式,即顺序阀运行,该种方式下,阀门会根据综合阀位指令相应地调整各自开度而不必保持同步。顺序阀运行可以有效地较小节流损失,但也带来了新的问题,如图2所示,阀组总流量为四个阀门总流量之和,单个阀门流量会受到其开度以及前后压比的影响,并且四个阀门的流量、阀后压力之间存在耦合影响。以某机组实际运行情况为例,当其中某个高调阀阀门开度改变时,会使得其阀后压力发生改变,进而对其余阀门阀后压力产生影响,改变其余阀门流量,并最终使得总流量发生变化。因此,尽管可将阀组流量主要影响因素归结为阀门开度以及压力,但因其两者之间存在耦合变化的关系,实际操作中很难使用常规方法直接建立流量与这两者的函数关系。

图2 进汽阀组间耦合影响示意图

2 阀门流量特性简化模型

2.1 阀门流量模型简化

将蒸汽在阀腔内的流动情况看作一个一维流动问题,不同型号、尺寸的阀腔看作是一个渐缩渐扩管。对于渐缩渐扩管而言,可按照喉部所在位置将其分为渐缩部分(喉部前)以及渐扩部分(喉部后),其中喉部即为阀芯与阀门内壁组成的截面,该截面大小会随着阀门开度的变化而变化。

由于在渐缩部分内蒸汽流速快,停留时间短,因此可将蒸汽在该部分的流动看作绝热等熵流动问题,对于渐缩管内的等熵流动,其流量与喉部面积相关,即流量主要受阀门开度影响。

根据流体力学可知,流体在渐扩管内的流动与管的几何尺寸以及管前后压力有关,对于确定的阀门其几何尺寸也是确定的,即流量主要与渐缩部分出口压力与渐扩部分出口压力(喷嘴入口压力)有关。而喷嘴又可类比于渐缩管从而看作是一个喉部面积固定的一维等熵流动,当喷嘴确定时,其进出口压力同样满足确定的函数关系,类推可知,阀门入口压力与喷嘴出口压力便也满足一定的函数关系。

因此,通过上述分析可知,汽轮机阀组的流量可看作是阀门开度以及压比(调节级压力与主蒸汽压力之比)的函数,如下式所示

G(ε,z)=f1(z)f2(ε)

(1)

式中G——流量函数;

f1——阀门开度函数;

f2——压比函数;

z——阀门开度;

ε——调节级压力与主蒸汽压力之比。

通过弗留盖尔公式可算得,汽轮机阀组总流量如下式所示

(2)

式中Q、Ptj、Pz、T——当前工况下蒸汽流量、调节级压力、背压以及主蒸汽温度;

Qe、Ptje、Pze、Te——额定工况下蒸汽流量、调节级压力、背压以及主蒸汽温度。

由于汽轮机主蒸汽温度变化很小,背压与调节级相差较大,因此,公式(2)可简化为下式

Q=αPtj

(3)

式中α——常数,数值上等于额定工况下蒸汽流量与调节级压力之比。

将公式(1)、公式(3)与流量与流量函数关系Q=CPG(ε,z)联立推导可得

ε=[f1(z1)+f1(z2)+f1(z3)+f1(z4)]f2(ε)

(4)

式中zi——第i个阀门的开度。

2.2 函数结构

为得到流量的计算公式,首先需要得到阀门开度函数与压比函数,本文利用实际数据通过拟合来得到阀门开度函数与压比函数,但是,为了提高拟合精度、降低拟合难度,还需要提前根据实际对象对函数做一些限制。

首先对阀门开度函数进行分析,阀门开度直接影响阀腔通道内的喉部面积,两者之间的对应关系也被称为固有流量特性,一般可分为快速开启、线性以及等百分比三种,如图3所示。但无论是哪种特性都满足以下特点:在阀门开度较小时,开度与喉部面积可近似看作线性关系,并且,该特点在一些仿真实验中也已经得到了验证。

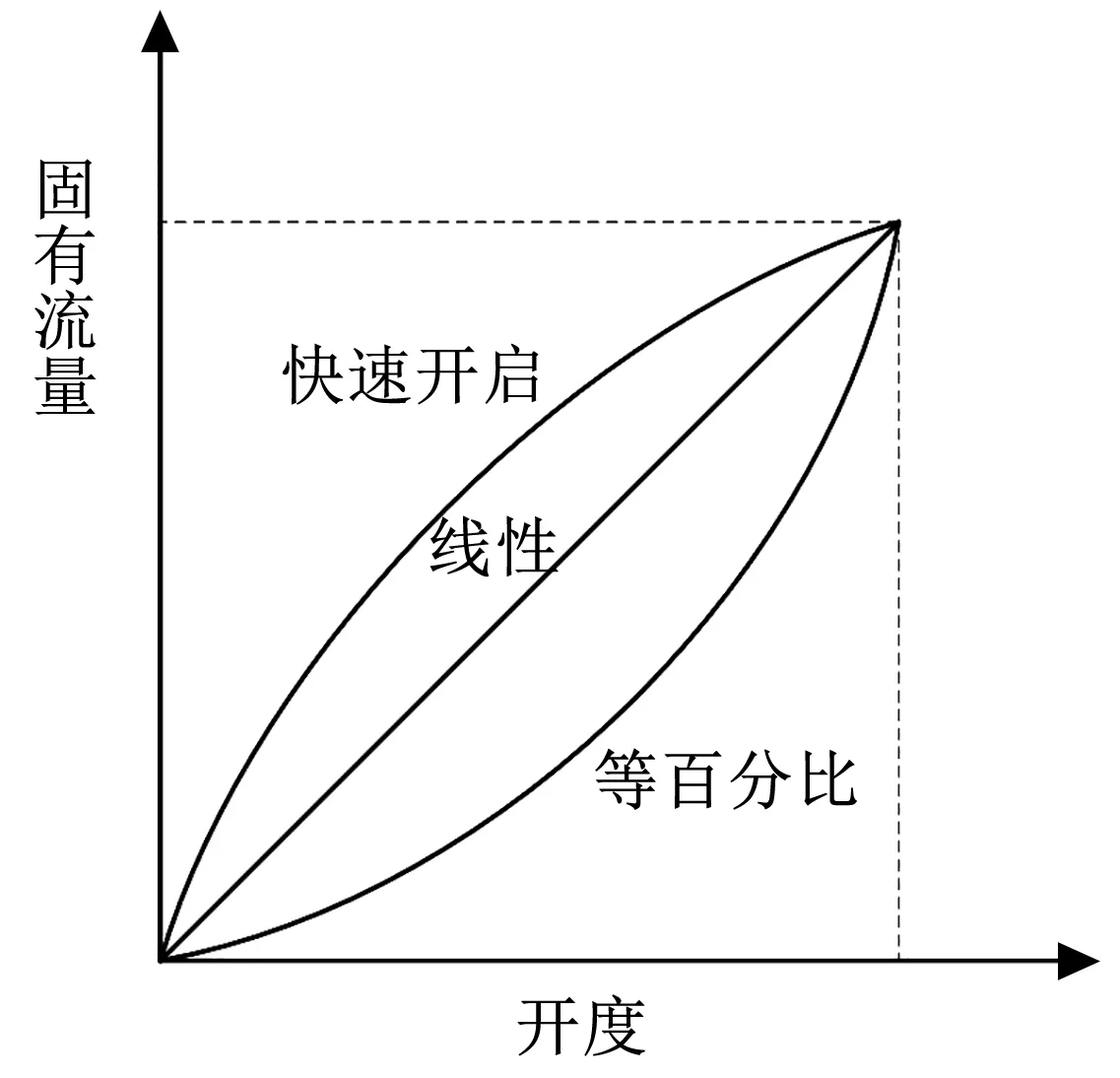
图3 阀门固有流量特性分类

当阀门开度增大到一定程度以后,即从物理结构上看阀芯与阀门内壁组成的截面积大于内壁通流面积时,阀腔内喉部面积将保持不变,即阀门开度还存在另一特点:当开度增大至一定程度后,几乎不会再对流量产生影响。

由此可知,阀门开度函数可看作一个分段函数,其存在两个分段点,可表示为如下式

(5)

式中z1、z1——开度较大或较大时的分界点;

在确定压比函数形式时,根据先验经验可知,当压比减小到一定程度时,流量将不再随压比减小而变化,因此,压比函数可以看作只有一个分段点的分段函数,如下式所示

(6)

式中ε1——压比函数分界值;

3 模型参数辨识及验证

3.1 辨识方法

阀门开度函数以及压比函数的形式在前文中已确定,但其中含有未知参数需辨识。由于阀门开度函数与压比函数均为分段函数,因此辨识过程也需要分段进行。

本文使用某台机组实际运行数据进行拟合,部分数据如图4所示,通过对机组数据进行观察并结合经验,可预设阀门开度函数及压比函数线性区分别划分为0～25%以及0～0.7,并将两者的非线性区用二阶多项式进行表示,如下式所示

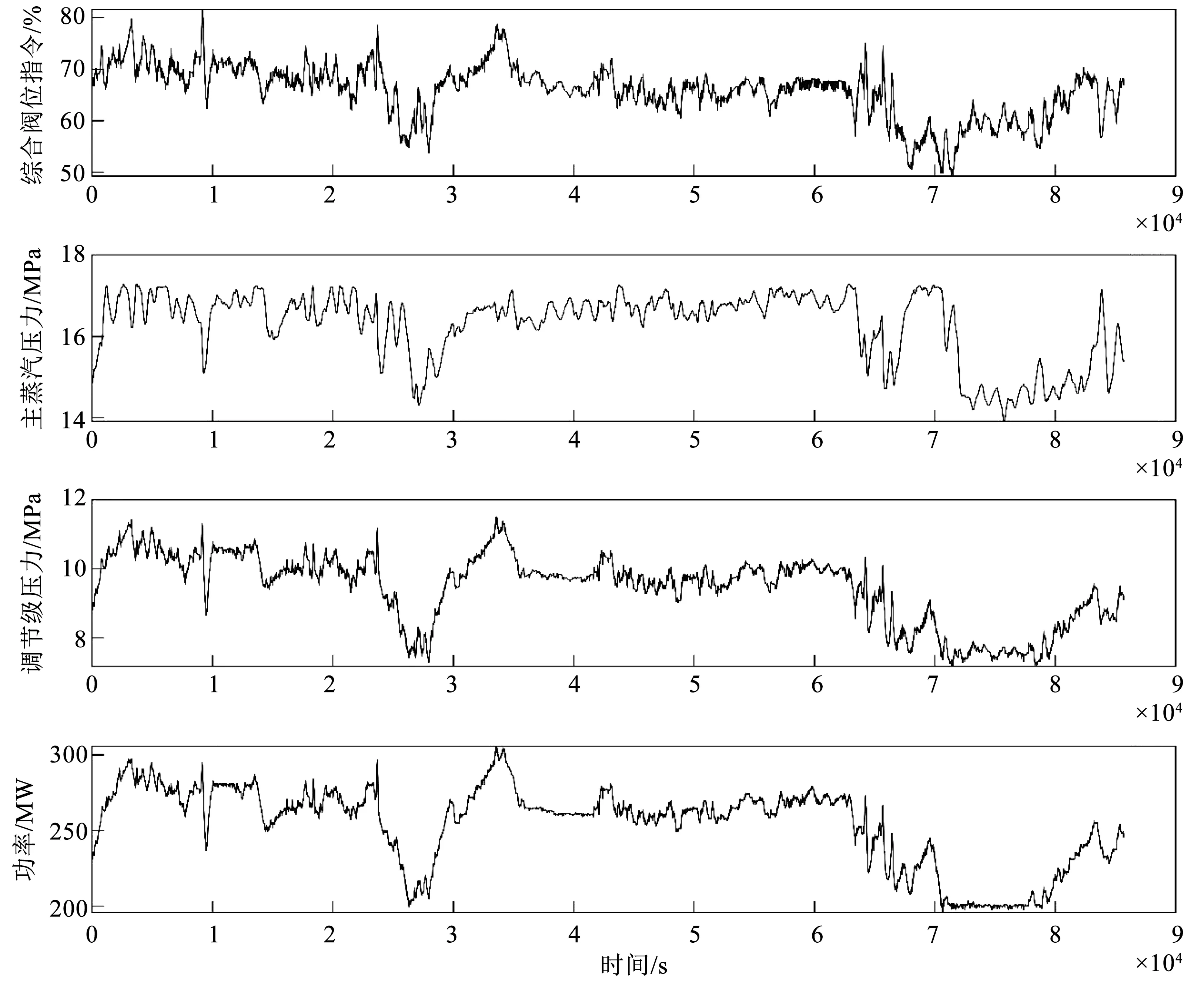
图4 机组运行数据

(7)

3.2 辨识结果

在得到压比函数及阀门开度函数的结构之后,本文按照函数分段区间,分别将实际数据划分为了线性区数据以及非线性区数据,并通过最小二分法对各段函数中未知参数进行了辨识,最后将各段函数加和得到压比函数及阀门开度函数分别如图5和图6所示。

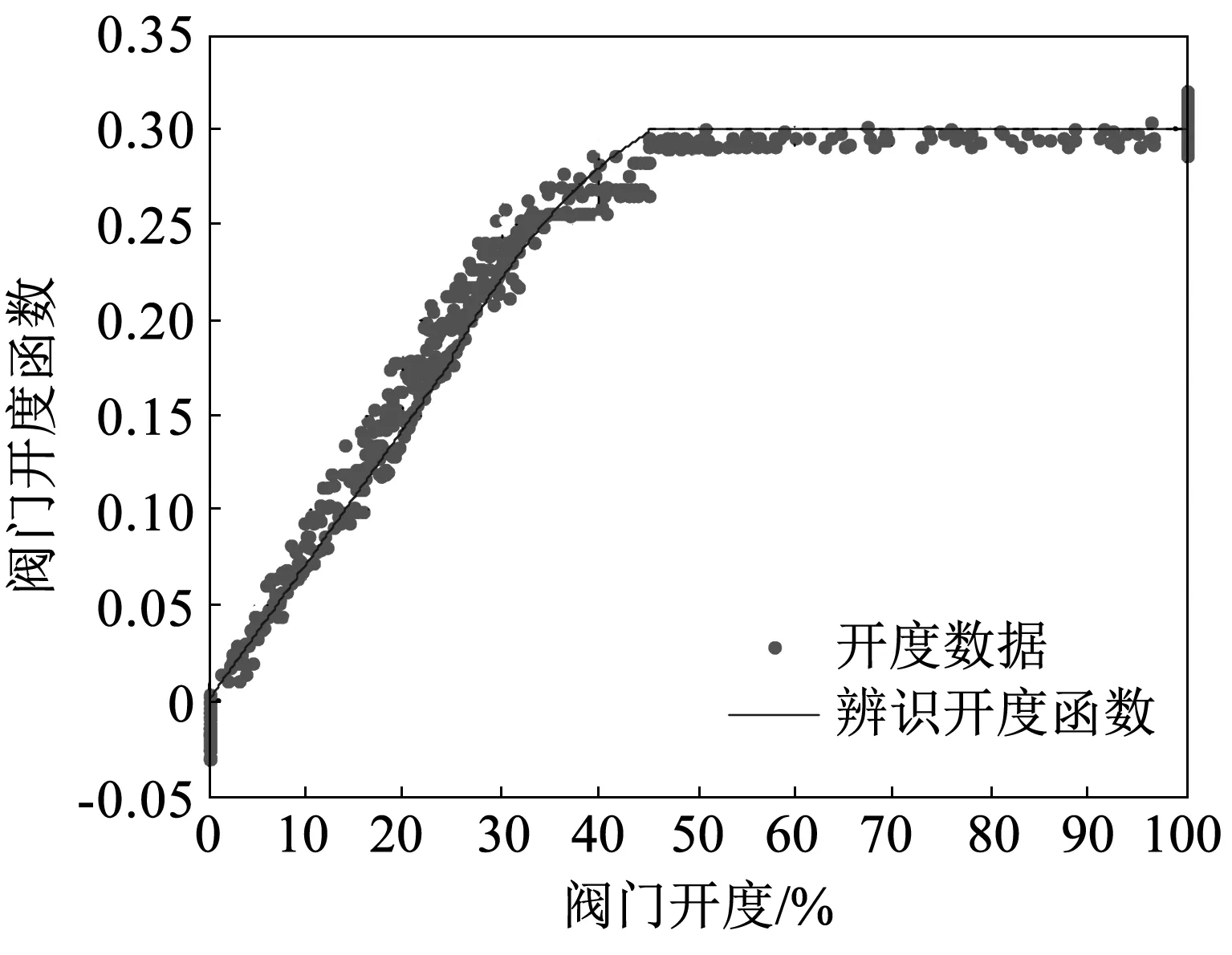
图5 阀门开度函数

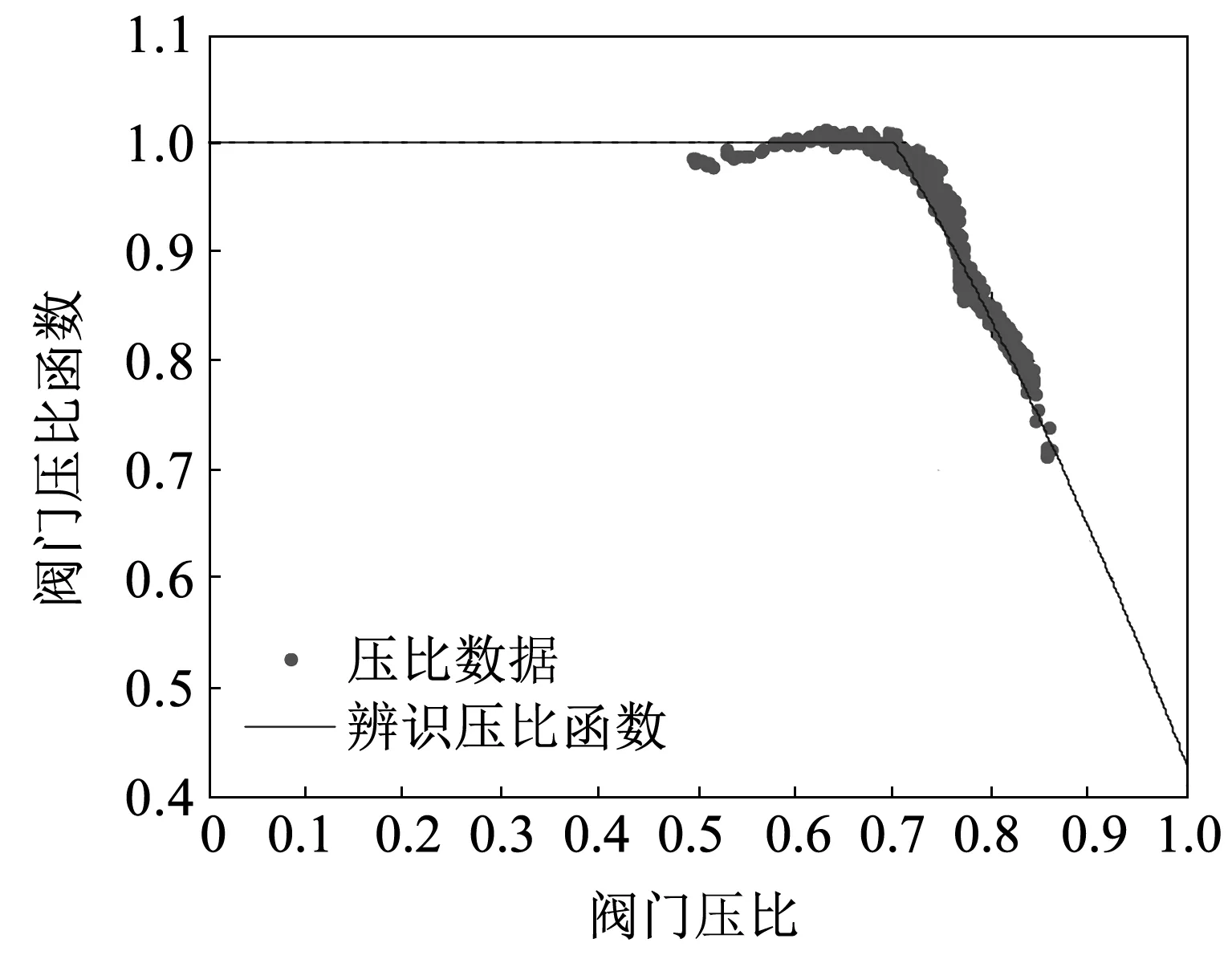
图6 压比函数

为验证拟合所得压比函数以及阀门开度函数的准确性,本文选择机组实际运行中,调节级压力与主蒸汽压力之比不同时,四个高调门所对应的开度作为基准,对本文辨识所得压比函数与阀门开度函数进行了准确性验证,如图7所示,结果表明,通过压比函数与阀门开度函数能够得到较为切合实际的阀门流量特性曲线。

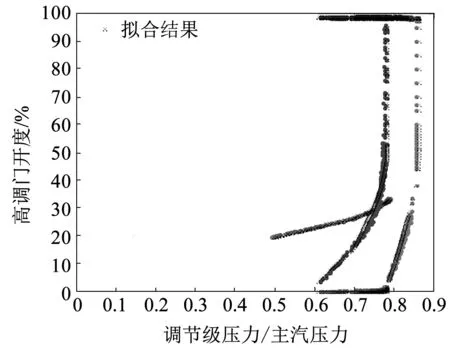
图7 拟合效果示意图

4 结论

本文针对获得阀门流量特性曲线过程中,由于高调阀各阀门开度与压比之间存在耦合变化关系而导致无法直接对阀门流量特性进行辨识的问题,通过对蒸汽在阀组间的流动进行分析,将之简化为一个喉部面积可变的一维渐缩渐扩管流动问题,并进一步将流动的影响因素简化至压比与阀门开度两项,分别通过压比函数与阀门开度函数来表征。之后通过先验知识对函数结构进行了限制以简化拟合难度,利用实际数据对函数进行了分段拟合,得到了该机组的压比函数与阀门开度函数,并验证了拟合效果的准确性,该方法可以实现进汽阀组间流动影响因素的解耦,具有更广的适用范围,可更为简便地得到较为切实的阀门流量特性曲线。