智能反射面赋能的联邦边缘学习及其在车联网中的应用

王平，杨志伟，李贺举

（1.同济大学电子与信息工程学院，上海 201804；2.上海自主智能无人系统科学中心，上海 201210）

0 引言

作为物联网中一个有潜力的研究分支，车联网可有效改善道路安全问题和驾驶者的驾乘环境，有望成为智能交通系统中重要的数据传输与控制平台。同时，随着下一代无线网络的蓬勃发展，以机器学习为核心的应用方案在分析车联网边缘数据方面发挥着重要的作用，可进行自主化的推理、建模以及决策[1]。然而，由于无线资源限制、时延约束及数据隐私安全方面的挑战，强迫车联网移动终端将其收集的本地隐私数据上传到中心节点（如云服务器进行集中模型训练）是不切实际的。为此，联邦边缘学习（FEEL,federated edge learning）通过允许分布式终端设备在数据本地化的前提下共享本地模型协同训练，避免敏感数据通过无线信道传输，从而有效地保证了车联网终端隐私和数据安全[2]。此外，中心节点从云服务器下沉到网络边缘，使移动终端只需与基站（BS,base station）端通信，由此显著降低通信成本，克服由网络拥塞导致的过度传播时延问题[3]。然而，由于采样对象或采样终端规格存在差异，移动终端数据往往是非独立同分布（non-IID,not identically and independently distributed）的，即各终端的本地数据往往不服从同一分布，表现出较大的差异性[4]。当数据是独立同分布（IID,identically and independently distributed），即局部分布相同时，局部损失函数在大量样本上收敛于相同的期望损失，而non-IID 数据则会影响全局模型的预测准确率，阻碍全局模型收敛，从而使联邦学习任务不能取得预期效果。

同时，由于移动终端通过无线信道连接到基站，基站端接收到的模型参数不可避免地受到信道衰落和加性噪声的影响[5]。由于终端间的无线环境不同，其与基站端的通信链路也存在较大的异构性。因此，在模型更新过程中设计有效的上行通信系统是FEEL 训练的关键问题。针对上行通信设计，目前已有研究主要利用正交信道来实现本地模型的并发上传[3,6]，以尽可能地避免终端干扰，然而，当边缘终端数量较多时，此种通信方式通信效率低下，且所需带宽资源较多。针对此问题，有工作设计了基于空中计算（Aircomp,over-the-air computation）的FEEL 无线聚合方案，以提升频谱效率。然而，绝大多数工作侧重于IID 设定下的空中计算分析与设计，其并未统筹考虑通信及non-IID 数据分布对空中联邦学习性能的影响。同时，由于无线环境的不可调控性，如何设计高效的空中聚合方案，并统筹规划无线资源分配方案，从而在有限资源约束下最大化联邦性能收益，仍然是一个亟待解决的问题。

近年来，智能反射面（RIS,reconfigurable intelligent surface）作为一种极具前景的通信新范例，引起了无线通信领域的普遍关注，其可为5G 和6G系统提供智能且可重构的无线信道传输环境。具体来说，智能反射面是一个二维平面，其由大量无源反射元件构成，并且每个元件都能对入射信号独立产生一个可控的振幅和（或）相位，这从根本上解决了无线信道衰落损伤和干扰问题。基于此，文献[7-8]将RIS 引入基于空中计算的FEEL 框架中，并以理论和实验证明RIS 在缓解空中聚合误差方面的有效性，然而，其工作依赖于IID 数据分布的假设。

为此，本文提出了一种non-IID 数据分布下智能反射面赋能的空中联邦边缘学习可靠通信方案。具体来说，本文利用智能反射面的信道可重构性来提高接收信号功率，并利用空中计算实现联邦边缘学习模型的快速聚合。本文的主要贡献如下。

1) 本文设计了智能反射面赋能的空中计算模型聚合方案。通过分析由non-IID 数据分布和无线信道衰落联合造成的模型聚合误差，本文推导出non-IID 环境下联邦边缘学习的训练损失上界。

2) 通过分析收敛损失上界，本文进一步构造关于收发端波束成形方案和RIS 相移矩阵的“通信-学习”优化问题，并引入一种低复杂度的凸近似策略，将非凸无线资源优化问题解耦，直到算法收敛。

1 相关工作

随着5G 技术的发展，移动边缘计算（MEC,mobile edge computing）[9-10]正在成为未来网络的一项关键技术，以在边缘网络下实现超低功耗和超低延迟应用。联邦边缘学习通过结合联邦学习和MEC，可有效增强边缘数据隐私和安全保障，以提供完备的边缘智能服务[11-12]。

然而，由于无线信道衰落和资源的有限性，通信效率成为在有低时延、隐私和安全保障需求的无线网络中大规模部署联邦学习的关键性能指标[3,6,13-14]。为此，文献[6]聚焦正交多址接入技术，分析了无线数据包传输误差对模型参数更新过程的影响，并通过优化用户选择和上行链路资源块分配方案，最小化训练损失。然而，基于正交多址接入的聚合方式拥有极低的频谱利用效率，其所需通信资源随着网络规模的增加而线性增长。针对这一问题，文献[13-14]研究了基于Aircomp的非正交多址接入聚合方案，其利用多址信道的波形叠加特性，将终端在宽带信道上同时传输的梯度更新进行模拟空中聚合，以此降低联邦学习通信开销，提升频谱资源利用效率。

然而，就现有的工作来说，基于Aircomp 的联邦学习聚合方案依然面临着一些亟待系统性研究的挑战，如弱信道补偿问题。具体来说，实现空中更新聚合需要从不同移动终端接收到的模型参数具有相同的振幅，因此，空中计算网络需要通过功率控制补偿不同终端的信道衰落，以满足空中计算所需的信道一致性，因此其性能会受限于边缘终端的弱信道，这在一定程度上损失了空中计算网络的通信性能增益。针对此问题，有必要刻画空中计算网络通信误差对联邦学习性能的影响，以此实现最优的“通信-学习”折中。文献[15-16]分别使用数据比例和所选终端数量来近似学习性能，并通过调整通信错误容忍度约束来实现“通信-学习”的统一规划。然而，上述工作可能不能完全描述联邦学习的训练性能，从而导致系统性能的损失。为解决这一问题，文献[17]开发了统一的联邦学习分析框架，来定量地描述模型聚合误差对空中计算FEEL 收敛性的影响，然而，其工作侧重于IID 数据分布下的学习设计，这一定程度上与联邦学习的non-IID 特性相违背。为此，文献[18]通过引入non-IID 数据分布引发的训练误差，设计了一种基于Aircomp的无线聚合方案，然而，其未考虑到FEEL“通信-学习”的联合设计问题。

综上，如何在non-IID 数据分布设定下，联合量化信道衰落及数据异构对联邦学习性能的影响，以此设计合理的无线资源分配方案，从而在有限的资源约束下最大化联邦性能收益，仍然是现阶段联邦学习亟待解决的重要问题。

2 问题描述

2.1 联邦学习模型

如图1 所示，本文考虑由一个J根天线的基站和K个单天线边缘终端组成的联邦边缘学习系统，其中部署了智能反射面辅助通信。边缘终端k∈{1,2,…,K}存有本地数据集Dk，其由已标记的Dk对数据样本特征和关联标签z={x,y} 组成。假设终端在基站的协调下合作训练一个全局模型参数向量w∈RD。定义损失函数f(w,z)，其量化模型w在训练样本z={x,y} 上的预测偏差。那么，从形式上来说，边缘终端k的局部学习目标是最小化本地数据集Dk上的经验损失函数，即

图1 系统模型

由此，联邦学习的全局优化目标可表示为

具体来说，联邦边缘学习框架可分为如下步骤。

1) 基站端将当前的全局模型（由最新的权重向量wt描述）广播给边缘终端。

2) 每个边缘终端将wt赋值给本地模型，即=wt，并使用其本地数据集在接收到的全局模型基础上来更新本地模型。为了降低non-IID 分布对学习性能的影响，首先利用FedProx算法[19]限制局部模型相对于全局模型的偏离程度，此时，终端k的局部学习目标可改写为

假定终端使用小批量随机梯度下降（SGD）本地训练E次迭代生成，其中单次更新过程总结为

2.2 RIS 赋能的空中计算模型

假设一个块衰落信道模型，其中信道系数在整个训练过程中保持不变。值得说明的是，本文的设计可容易扩展到非块衰落信道时的情况，仅需要在每次迭代开始之前适当地进行信道估计和参数求解。RIS 由L个被动反射元件组成，记为L≜ {1,2,…,L}，其与控制器关联，并且，控制器通过调节RIS 元件的反射系数来控制信号反射。在RIS 控制器和BS 之间部署了单独的控制链路，以获取反射系数设计所需的信息[18]。定义终端k-BS、终端k-RIS 和RIS-BS 的信道系数分别为∈CJ、∈CL和G∈CJ×L。并且，对于每个信道，假设信道状态信息（CSI）在BS 和RIS 上都能完美估计。假设FEEL 模型聚合过程中，RIS 相移保持不变。Θ=diag {θ} ∈CL×L表示 RIS 相移矩阵，其中，=1。

如上所述，终端k-BS 路径有效信道系数可表示为

本文拟采用空中计算技术实现FEEL 模型的快速聚合。具体来说，边缘终端使用相同的无线电资源并发地传输其本地模型更新。接着，BS 利用信道的信号叠加特性，从接收到的信号中恢复聚合模型。与传统的正交多路访问协议（终端使用正交信道传输）相比，空中计算的带宽需求或通信时延不随终端数量的增加而增加，极大地缓解了FEEL 中的通信压力。

在第t轮模型聚合中，将梯度传输时间划分为D时隙。定义时隙d∈{1,…,D}中终端k的发射信号为{[d]}，则BS 端处对应的接收信号 {yt[d]}，其为直线信道与终端-RIS-BS 级联信道信号的叠加，即

其中，n[d]∈CJ表示加性白高斯噪声（AWGN）向量，其分量服从分布 CN（0,）。

2.3 基于空中计算的模型聚合

将式(10)代入式(8)，BS 端在时隙d上的接收信号为

3 收敛分析及问题建模

接下来，着重阐述RIS 赋能的联邦边缘学习系统收敛理论，并具体分析无线信道及RIS 对空中联邦学习全局模型收敛上限的影响。

3.1 基础假设

首先，对用于收敛性分析的假设和定义进行说明。

上述假设在联邦学习收敛性分析中被广泛地采用，参考文献[16,20-21]。

3.2 收敛分析

在上述假设的基础上，本节给出RIS 赋能的空中联邦边缘学习系统收敛性定理。

证明过程见附录1。

上述收敛上界依赖于联邦边缘学习系统通信环境的配置，即智能反射面相位设计和收发端波束成形设计。直观地说，由通信引入的误差会累积起来，并反映在新的全局模型中，从而影响FEEL 的收敛性。若上述通信配置设计得当，收敛速度可以在很大程度上得到保证。由定理1 还可以看出，收敛上界与超参数有一定的单调关系。例如，边界随着E的增大而增大，这与文献[22]的结果一致。并且non-IID 数据分布的影响体现在Γ引入的误差项上。当Γ减小时，收敛上界单调减小；当Γ趋于零时，可得到IID 数据分布的收敛上界。

3.3 问题建模

参照定理1，空中计算通信系统会在收敛上界中引入一个误差项，其揭示了智能反射面相位偏移设计和收发端波束成形对收敛速度和学习性能的影响。越大，学习性能越差。由此，可以建立一个关于收发端波束成形方案和RIS 配置矩阵的“通信-学习”优化问题，表示为

4 联合优化

上述问题仍然是非凸的。为此，本文采用拉格朗日对偶算法将其近似。定义拉格朗日对偶向量ξ=[ξ1,ξ2,…,ξK]T≥0，则上述对偶问题表示为

由此，f(i+1)和θ(i+1)可通过求解以下的优化问题得到

等式成立。ξ可通过求解以下优化问题得到

当式(29)用凸优化求解器求解时，若采用内点法，其最坏情况复杂度上界为O(K3)。假设最大迭代次数为Imax，则 SCA 策略复杂度上界为O(ImaxK3)。

5 实验设计与分析

接下来，通过仿真实验评估所提方法的性能，并与几种基准方案作比较。

5.1 实验设定

如图2 所示，本文考虑三维笛卡儿坐标系下的仿真设定。其中，BS 和RIS 分别放置在(-50,0,10)和(0,0,10)处。边缘终端随机分布在2 个半径为10 m的圆形区域，即区域 I ∝ {（x,y,0）:-20≤x≤0,-10≤y≤10}以及区域Ⅱ ∝{（x,y,0）:100≤x≤120,-10≤y≤10}。简单起见，假设终端中有一半随机分布在区域I，另一半随机分布在区域Ⅱ。

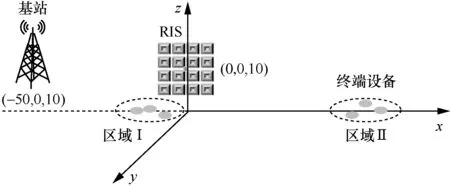
图2 仿真设定

与文献[18]类似，本文相关信道系数定义为大尺度衰落和小尺度衰落之积。具体来说，小尺度衰落服从标准高斯分布，并且终端到基站端的路径损耗模型表示为

其中，GBS和GD分别表示基站端和终端的天线增益；fc表示载波频率；PL 表示路径损耗因子；表示终端到基站端的距离。终端-RIS-BS 的路径损耗模型建模为

其中，GRIS表示RIS 端的天线增益；dx和dy分别表示RIS 单元的水平和垂直大小；dRB及dDR分别表示RIS 到基站端的距离以及终端到RIS 端的距离。如无特别说明，仿真参数如表1 所示。

表1 仿真参数

在FEMNIST 数据集[24]上执行图像分类任务，以验证所提方法性能。具体来说，首先构建一个4 层的卷积神经网络（CNN），其中包括2 个5×5 卷积层以及2 个全连接层。为了展现所提方案（OPT）的性能，本文设置了如下的基准方案进行了性能比较。

1)DGP：无RIS 辅助通信，即θ=0。通过微分几何规划[25]，设计接收机波束成形矢量f，以最小化通信均方误差。

2) RDGP：采用随机RIS 相移，并通过微分几何规划，设计接收机波束成形矢量f，以最小化通信均方误差。

3)SDR：针对问题P，RIS相移θ以及接收机波束成形矢量f通过半正定松弛算法[26]迭代优化。

此外，将无噪声传输方案（S-FedAvg）作为性能上界，用于比较。

5.2 性能分析

图3 展示了non-IID 设定下的联邦学习测试精度比较。从图3 可以看到，本文方案取得了比其他基准方案更优异的收敛性能。并且，值得一提的是，相较于无RIS 辅助的DGP 设计，除了本文方案，其余3 种方案都实现了显著的性能提升，这证明了在non-IID 设定下，RIS 同样可以提高空中FEEL系统准确性。

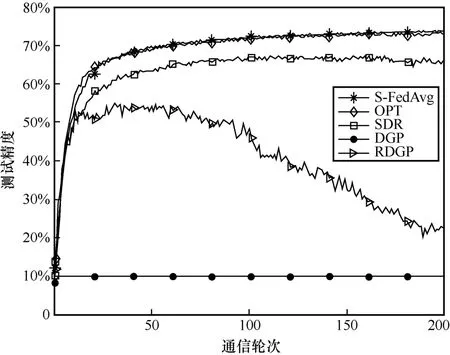
图3 non-IID 设定下的联邦学习测试精度比较

图4 展示了IID 设定下（即Γ=0）的联邦学习测试精度比较。从图4 可以看出，相较于non-IID设定，SDR、OPT 以及S-FedAvg 皆实现了一定程度的性能提升，原因在于，当Γ=0时，定理1 所示的收敛上界中消除了关于non-IID 数据分布的误差项，提升了学习性能。

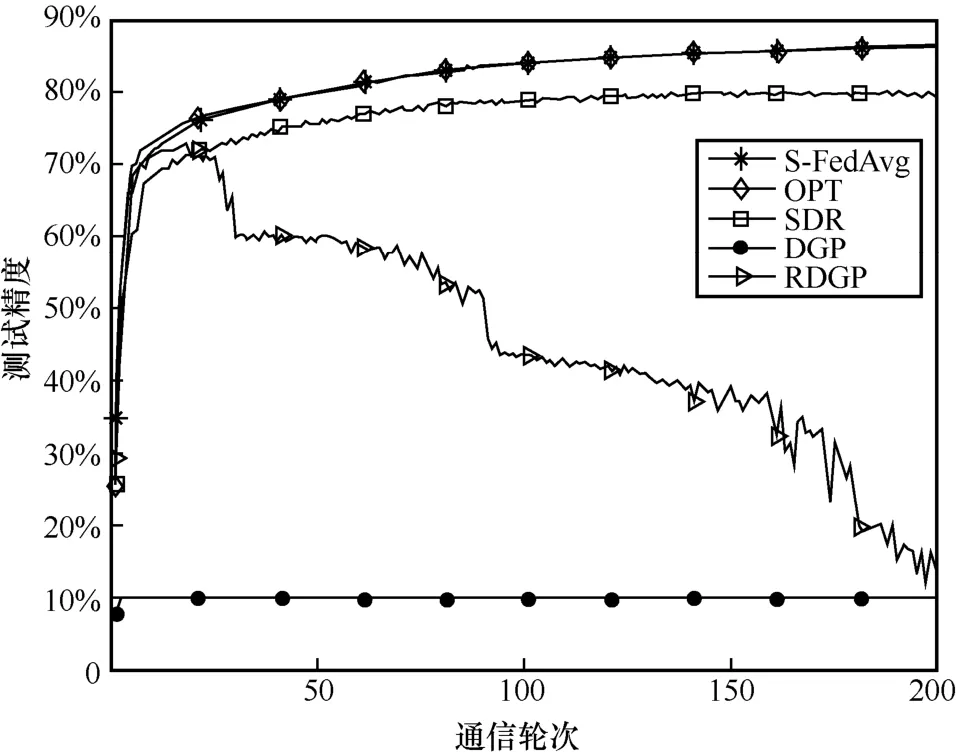
图4 IID 设定下的联邦学习测试精度比较

图5 展示了non-IID 设定下不同反射单元数量对测试精度的影响。显然，SDR 和OPT 都可以在较多的反射单元数量下实现相当大的性能提升，这是因为反射单元数量的增加会提高调配智能反射面适配信道的自由度，即通过设计智能反射面的相移产生更窄波束形成，以增加通信链路的可靠性，降低基站端的聚合误差。然而，所提方案与其他方案之间的性能差距仍然存在。

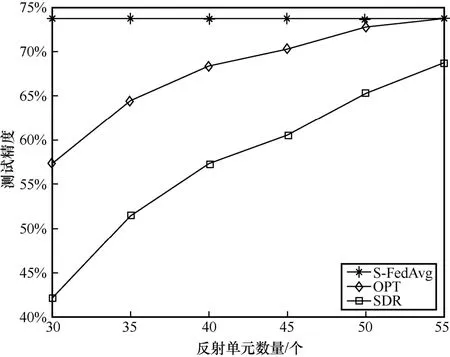
图5 non-IID 设定下不同反射单元数量对测试精度的影响

如图6 所示，进一步假设每个RIS 相移只能取有限个离散值，即

图6 non-IID 设定下不同离散比特对测试精度的影响

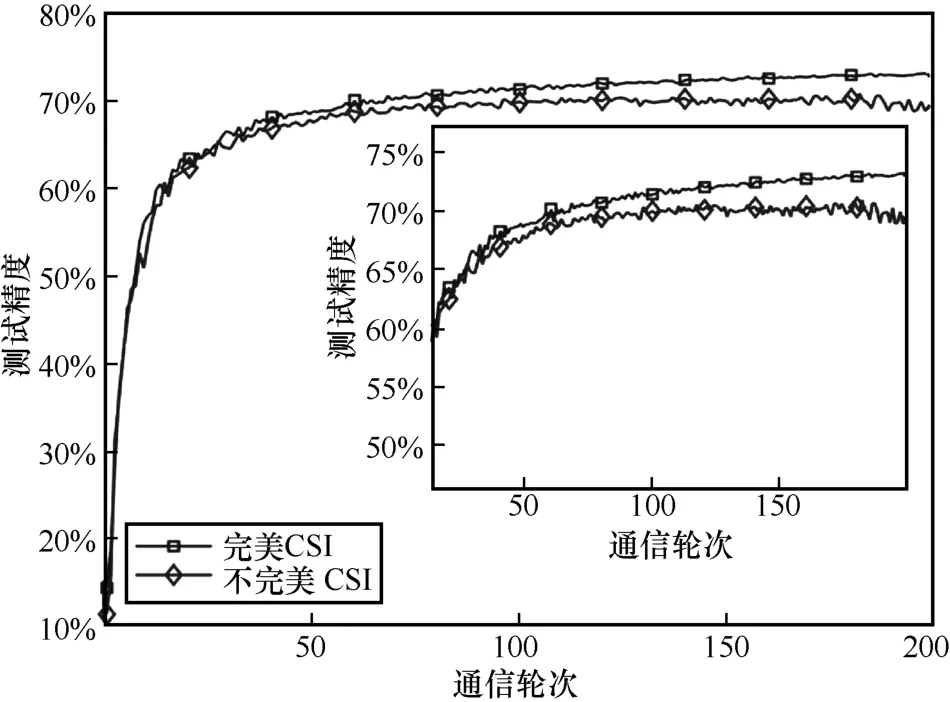
图7 non-IID 设定下不完美CSI 对测试精度的影响

6 在车联网中的应用探讨

在特大城市如北京、上海，车辆或其他移动终端容易受高层建筑遮挡而造成信号传播盲区，将RIS 安装在视野更开阔的建筑物表面，可以中继移动终端的信号给基站，利用智能反射面的信道可重构性来提高接收信号功率，并利用空中计算实现模型的快速聚合增强无线资源的收益，如图8 所示。

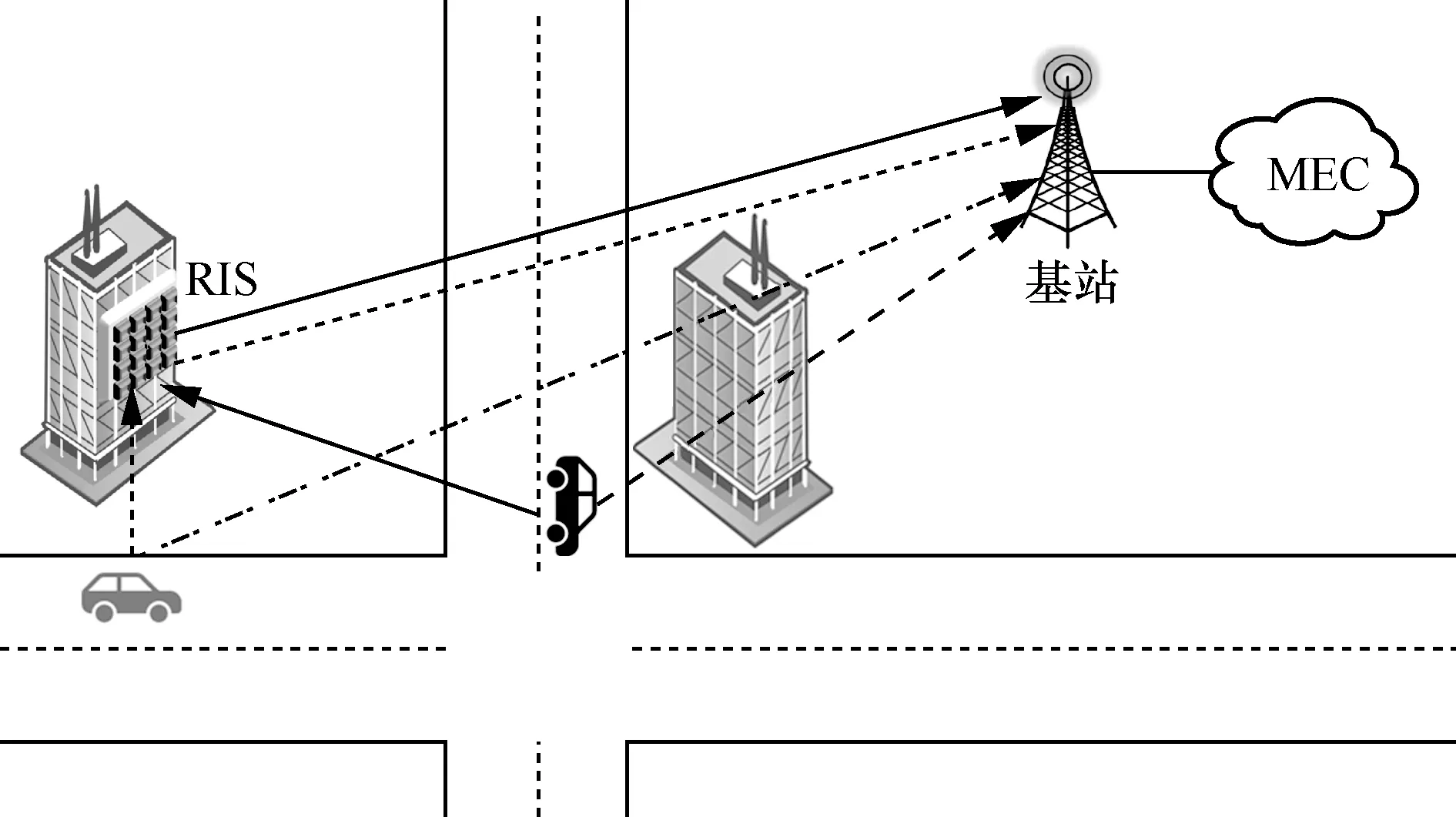
图8 智能反射面赋能的联邦边缘学习在车联网中的应用

7 结束语

针对non-IID 设定下的联邦边缘学习框架，本文提出一种智能反射面赋能的空中计算聚合模型。通过量化由non-IID 数据分布和无线信道衰落共同引起的模型聚合误差，首先推导出non-IID 环境下空中联邦边缘学习的训练损失上界，并以此为基础，建立通信资源约束下以收发端波束成形和RIS 相移为变量的损失上界最小化问题；同时，引入一种低复杂度的凸逼近策略，高效求解最优通算参数，以减弱甚至消除通信误差对联邦学习收敛性能的影响。最后，通过仿真实验验证了所提方案的有效性。

未来，将考虑更多通用的场景，例如非凸损失函数下的“通信-学习”联合建模和折中优化，以及引入模型量化技术进一步降低传输开销等，从而为深层次理解联邦边缘学习融合无线通信新范式提供新的理论支撑。另外，还可探讨将RIS 用于V2V（vehicle to vehicle）场景，有助于消除移动终端之间信号干扰，增强每个移动终端的接收信号质量。

附录1 RIS 赋能的空中联邦边缘学习系统收敛性证明

首先，定义时间轴刻度为SGD 更新轮次，如式(33)所示

接下来，引入在定理1 的证明过程中一些必要的引理，其具体证明过程参考文献[20]。其中，引理1 是根据损失函数的光滑性和凸性推导出来的；引理2 源于SGD 方差有界性，而引理3 由损失函数的有界梯度导出。

当t+1∈IE时，边缘终端通过空中计算网络将其模型传输到BS 端并解码，则有