基于编码分布式快速哈达玛变换的多元LDPC 码译码算法研究

刘锐，黎勇

（重庆大学计算机学院，重庆 400044）

0 引言

非二元/多元 LDPC（NB-LDPC,non-binary LDPC）码是由二元LDPC 码在有限域（GF,galois field）上扩展而来的[1]。相比二元LDPC 码，多元LDPC 码更好地消除了Tanner 图中的短环，提高了纠错性能[2]。多元LDPC 码用多个比特表示一个多元符号，获得了较二元LDPC 码更好的抗突发错误能力[3]。另外，多元符号与高阶调制更匹配，提升了频谱利用率[4]。

尽管多元LDPC 码有多重优势，但其更高的译码复杂度极大地阻碍了多元LDPC 码的实际应用。多元LDPC 码的译码算法以多元和积算法（QSPA,q-ary sum-product algorithm）为代表[1]，后续针对QSPA 计算复杂度问题，研究者提出了FHT-QSPA[5]、FFT-QSPA[3]等改进算法。此外，Min-Max[6]、Min-Sum[7]、EMS[8]等译码算法简化了QSPA 中的迭代步骤，如替换和积操作、降低信息传递数量等，以不同程度的纠错性能损失换取了译码复杂度的降低。现有多元LDPC 码的硬件加速多基于简化译码算法展开，并在FPGA 和GPU 等专用芯片的支持下实现更高的译码吞吐量[9]。

因此，若要在单点计算资源有限且难以搭载昂贵专用芯片的设备上应用低误码率、高复杂度的多元LDPC 码QSPA 译码，则可借鉴分布式计算思路，利用多个节点的算力，共同完成计算密集型的译码任务，从而在纠错译码性能和算法复杂度两方面做出更好的折中。

但是，多节点分布式系统中某些节点可能出现通信繁忙、资源抢占、节点失效等情况，从而影响整体任务。这些节点被称为掉队节点。为了克服节点掉队的问题，传统的副本策略使用多个节点负责相同的任务，只要任意节点完成当前任务即可继续后续计算。然而，副本策略中成倍增加的资源消耗使其在资源利用率方面表现欠佳。

近年来，编码分布式计算（CDC,coded distributed computing）（简称编码计算）借鉴编码理论，巧妙地在计算任务中嵌入了冗余信息，克服了节点掉队问题、保护了数据隐私、优化了通信负载，成为分布式计算领域的研究热点[10-13]。以主从架构的编码计算方案为例，主节点能够通过部分从节点的计算结果直接恢复出掉队节点的计算结果，完成整体计算，克服掉队节点的拖累[10]。

在诸多编码计算研究中，大规模矩阵乘法（矩阵-矩阵/矩阵-向量乘法）作为机器学习算法的核心模块受到了较多关注。多项式码编码计算方案在矩阵乘法中嵌入了多项式结构[11]，使主节点可以通过部分从节点结果左乘编码系数矩阵的逆矩阵，求出掉队节点的计算结果。然而多项式码的编码矩阵作为一个范德蒙矩阵，其条件数随节点数量增加呈指数级增加，极大地影响了编码矩阵求逆，导致该方案在实数矩阵的译码恢复上数值稳定性很差。针对此问题，文献[12]通过切比雪夫多项式进一步改进了多项式嵌入结构，大幅提升了译码恢复过程的数值精度，使实数域上的编码分布式矩阵乘法成为可能。此外，文献[13]设计了一套基于系统型MDS（max distance separable）码的矩阵-矩阵乘法编码计算方案，其编码系数矩阵为随机系数矩阵，不具备范德蒙矩阵结构，在保证可译码性的同时，不会产生译码恢复过程的数值稳定性问题。但是，该方案仅进行了理论推导，未进行实验验证。

除了关注矩阵乘法，编码计算还研究了如何利用掉队节点的部分计算结果[14]计算稀疏性保持[15]等问题。此外，编码分布式计算也嵌入了边缘计算架构[16]、多无人机集群[17]等应用场景，为多种单点资源有限的分布式集群性能优化提供了新方案。

本文受系统型MDS 码编码计算方案[13]启发，针对多元LDPC 码的FHT-QSPA 译码，设计了FHT的编码计算加速方案，提升了多元 LDPC 码FHT-QSPA 译码的效率。具体来看，本文的贡献有以下三点。

1) 提出了基于系统型MDS 码的编码分布式FHT 方案。该方案在主节点上将信道概率建模为矩阵并对其进行切分，再编码生成冗余子矩阵；其后，将所有子矩阵卸载到从节点并行执行FHT 和IFHT，然后将计算结果传回主节点并完成最终译码。

2) 在子矩阵编码中，通过随机系数编码生成了冗余子矩阵，嵌入了冗余信息，克服了节点掉队问题；同时，本文证明了随机系数编码矩阵能够以概率1 的可能完成译码恢复，且恢复误差很小。此外，本文方案还保持了FHT 的高效蝶形运算结构。

3) 多个不同参数多元LDPC 码的耗时对比和译码性能分析表明，编码分布式FHT 方案相比传统单节点FHT 方案最高加速了约3.8 倍，显著提升了FHT-QSPA 译码效率，且没有译码性能损失。

1 相关工作

定义在有限域GF(q)上的多元LDPC 码可称为q-元LDPC 码，其中q=pr，p为素数，且r〉 1。令α表示有限域GF(q)的本原元，则有限域GF(q)中的所有元素均可用本原元的幂次来表示，即αi,i∈{0,1,…,q-2,-∞}，其中α-∞0。当p=2时，GF(2r)表示二元域的扩展域，其中每一个元素都可以唯一地映射为一个长为r的二元序列。因此，GF(2r)上的多元LDPC码的码字符号可以由r个二进制比特来表示。与二元LDPC 码不同，多元LDPC码的校验矩阵中的非零元不是1，而是有限域GF(q)中的q-1个非零元αi,i∈{0,1,…,q-2}，即一个(n,k)q-元LDPC 码C 可由有限域GF(q)上的校验矩阵Hm×n=[hi,j]的零空间来定义，其中，hi,j是有限域GF(q)中的元素。合法码字c和校验矩阵H的乘积为0，即HTc=0。

多元和积算法（QSPA）（又称BP 算法）是多元LDPC 码的经典译码算法。在QSPA 译码中，一次迭代译码可大致分为校验节点更新，变量节点更新和尝试译码三步[9]。针对QSPA 译码校验节点更新复杂度高的问题，文献[13]提出了等效变换，改进了每个有限域元素相应概率的计算方式，通过快速哈达玛变换代替了校验节点更新中的乘积操作，加速了译码算法。令表示变量节点n的值为有限域元素a时校验节点m被满足的概率；表示变量节点n的值固定为a时校验节点m被满足的概率。集合 N(m)表示与校验节点m相连的变量节点的集合。FHT-QSPA 译码的校验节点更新具体步骤如下。

1) 等效变换

其中，÷操作表示有限域上的乘法逆操作。

2) 快速哈达玛变换

3) 逆快速哈达玛变换

其中，⊗表示有限域上的乘法操作。

式(1)～式(4)表示FHT-QSPA 校验节点更新过程，需要根据校验矩阵中的非零元素对信道概率向量进行两组变换。若将校验矩阵所有非零元素对应的各符号信道概率表示为一个矩阵，则FHT-QSPA在校验节点更新过程的各计算步骤复杂度如表1 所示。复杂度最高的是FHT 及IFHT，为 O(r×2r×N)，其中，r表示扩展域阶数，2r表示有限域元素数量，N表示校验矩阵中非零元素数量。

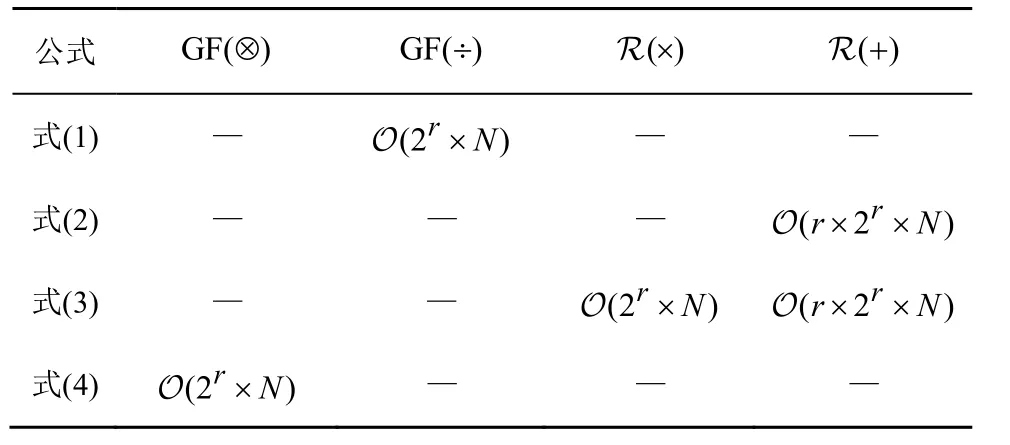
表1 校验节点更新过程的各计算步骤复杂度

在上述四步变换中，主要包括有限域上乘法GF(⊗)和有限域上乘法逆运算GF(÷)，以及实数域上的乘法 R (×)和加法 R(+)。式(1)和式(4)对应的是等效变换和逆等效变换，这两步在有限域上的乘法和乘法逆运算可以通过LUT（lookup table）来加速。而式(2)和式(3)所代表的FHT 和IFHT 是对浮点数类型的信道概率值进行更新。当码字有限域增大或码长增加时，FHT 和IFHT 的计算复杂度也随之快速增大。

表2 统计了定义在不同有限域以及不同码长的多元LDPC 码在单次校验节点更新中FHT和IFHT 两步耗时之和占单次校验节点更新总耗时的比例。由表2 可知，不同码长的FHT 耗时和IFHT 耗时之和超过了单次校验节点更新耗时的82%；而随着码字有限域增大，其耗时占比超过90%，成为校验节点更新的主要性能瓶颈。若通过分布式并行加速FHT 和IFHT，则可加速多元LDPC 码校验节点更新，从而加速整体译码过程。

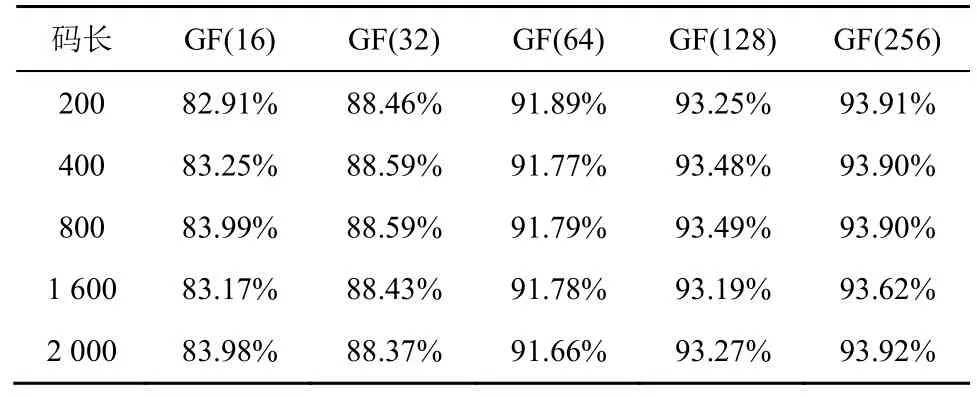
表2 FHT 和IFHT 耗时占比

2 系统型MDS 码编码分布式FHT 方案

正如前文分析，当校验矩阵中非零元素增加时，式(2)的规模快速增大。例如，当有限域阶数为64，校验矩阵中非零元素数量为600 时，需要变换的qmn矩阵大小为64 ×600。此时，单节点执行FHT需要进行 6×64×600=230 400次加减法操作。此时，若使用分布式计算，则可以将qmn矩阵划分为多个子矩阵，并将其卸载到从节点中并行执行，提高FHT 效率。

然而，在分布式计算的实际场景中，各计算节点受计算优先级、网络通畅程度等因素的影响，可能呈现出不同的计算速度。这样的节点掉队现象使分布式并行的加速效果受到部分掉队节点的拖累，降低整体加速效果。因此，针对FHT 设计一套抗节点掉队的分布式并行加速算法成为加速多元LDPC码译码的关键所在。

2.1 总体流程

设有一个n+1个节点组成的分布式计算系统，其中，主节点W0负责FHT-QSPA 的总体执行、子矩阵编码和掉队结果译码恢复。首先，主节点按列划分概率矩阵 [qmn]2r×N得到子矩阵序列B={B1,B2,…,Bk}。其后，主节点对子矩阵序列进行随机线性组合，得到编码子矩阵。之后，主节点将计算复杂度最高的FHT 和IFHT 卸载到从节点Wi,i∈{1,2,…,n}中并行执行。其中，k个从节点收到的是未编码子矩阵，而另外n-k个从节点收到的是编码后的子矩阵。从节点Wi分别对子矩阵进行FHT，并将计算结果返回给主节点。主节点只需收到最快完成的k个子矩阵变换结果便能恢复其他掉队子矩阵变换结果，从而克服了掉队节点对总体计算速度的拖累。方案整体流程如算法1 所示。

算法1基于系统MDS 码的编码分布式FHT方案

图1 展示了由5 个从节点组成的编码分布式FHT 方案，其中前3 个节点计算未编码子矩阵，后2 个节点计算编码子矩阵。主节点将FHT 卸载到各个从节点上，主节点上仅需要进行编码和译码操作。多个从节点收到了尺寸更小的子矩阵，并行执行FHT，实现分布式并行加速。图1 中×所示节点为掉队节点，而主节点可基于其他节点结果恢复掉队节点的计算结果。

图1 编码分布式FHT 方案架构

下面将围绕主节点编码环节、可译码性证明、译码环节和从节点FHT 计算来展开分析。

2.2 编码环节

首先，本节详细描述了系统型MDS 码编码分布式FHT 方案的子矩阵编码思路。主节点按列切分概率矩阵得到子矩阵序列B={B1,B2,…,Bk}。

此时，其上半部分I为单位矩阵，而下半部分为标准高斯分布 N(0,1)上采样的随机数子矩阵PB。因此，通过生成矩阵和未编码子矩阵序列的乘法，即可求出分配给所有从节点的子矩阵序列B

PB中的每行确定了一组随机系数，对未编码子矩阵进行线性组合，得到对应的编码子矩阵。即=bi,1B1+…+bi,kBk,i∈{k+1,k+2,…,n}。

此外，特别值得指出的是，在式(6)中，子矩阵Bi被视为标量，生成矩阵GB中对应的单位矩阵I维度也设定为矩阵划分后的子矩阵数量，即k×k。然而，实际情况中，每个子矩阵Bi的维度是。因此，编码环节仅需要针对未编码子矩阵进行随机系数标量和子矩阵的乘法，之后再进行线性组合，即可求出对应的编码子矩阵。

2.3 可译码性证明

本节分析系统型MDS 码编码分布式FHT 方案的可译码性。通过对其编码矩阵行列式的分析，证明其子方阵行列式以概率1 的可能是一个非零多项式，从而证明该方案能够以概率1 的可能完成译码。

引理1[18]若矩阵G的每一个子方阵都是非奇异矩阵时，该矩阵可以成为一个系统型MDS 码的编码矩阵。

引理2若子矩阵PB中的元素都是在标准高斯分布中 N(0,1)独立同分布地采样，子矩阵PB的每一个子方阵都以概率1 的可能是非奇异矩阵。

证明首先通过数学归纳法证明任意r×r阶子矩阵(r≤(n-k))的行列式都是非零多项式。当r=1时，假设显然成立。接着，假设每一个(r-1)×(r-1)阶子矩阵的行列式都是非零多项式。此时，任意一个r×r阶子矩阵可写为

此矩阵的行列式可以写为

在引理1 和引理2 的基础上，本文给出下列定理。

定理1若编码计算方案由生成矩阵G确定，PB为矩阵G的子矩阵，其大小为(n-k)×k，且PB中的元素均为标准高斯分布 N(0,1)中的独立同分布采样得到。此时，该方案给定了一个系统型的MDS 码编码计算方案，当主节点收到n个子矩阵变换结果中的任意k个时，即可以概率1 的可能译码恢复掉队节点对应的子矩阵变换结果。

在定理1 所确定的系统型MDS 码编码计算方案中，从节点数量为n个，其中有k个节点执行未编码子任务，有n-k个节点执行编码子任务。此时，该方案的恢复阈值为n-k，即该方案最多可以容忍n-k个节点掉队或失效。

2.4 译码环节

在n个从节点和一个主节点组成的分布式计算系统中，简便起见，可令前k个节点为未编码子任务节点，后n-k个节点为编码子任务节点。设从节点索引集合为i∈{1,2,…,k,k+1,…,n}，则2 种节点对应索引集合可规定为Iu={i1,i2,…,ik}和Ic={ik+1,ik+2,…,in}。

由定理1 可知，当主节点收到最快完成的k个子任务结果时即可完成计算。此时，主节点根据接收到的未编码子任务计算结果数量nu来判断是否需要进行译码。最好情况下，前k个未编码子任务都很快完成了计算任务，并将结果返回给主节点，即nu=k。此时，由于主节点收到了所有想要的未编码子任务计算结果，并不需要进行译码恢复，可直接进行后续计算任务。

而当nu〈k时，即未编码节点出现了掉队情况，则主节点需要收到至少k-nu个编码子任务计算结果来恢复未编码子任务的计算结果。设主节点收到nc个编码子任务节点结算结果，2 种节点对应的索引集合分为Su={u1,u2,…,unu},Su⊂Iu；Sc={c1,c2,…,cnc},Sc⊂Ic，且nc+nu=k。此时，主节点已经收到了足够数量的子任务结果，来恢复掉队节点子任务结果Ss=IuSu，完成译码恢复。

于是，可以得到下列由已知的编码子任务计算结果、未编码子任务结果、掉队未编码子任务结果确定的方程组

因此，掉队的未编码子任务结果可以通过求解上述方程组来获得。此时方程组(9)中的未知数为FHT(Bs),s∈Ss，未知数的数量ns≤nc，即掉队的未编码子任务的数量小于或等于主节点收到的编码子任务数量。此外，由定理1 可知，若编码矩阵中的系数为高斯分布中独立同分布采样得到，则满足任意r阶子矩阵均是非奇异矩阵，即任意r阶子矩阵均为可逆矩阵。根据上述两点，对方程组(9)进行求解即可得到掉队的未编码子任务结果FHT(Bs),s∈Ss。

例如图1 所示的编码分布式FHT 方案，由5 个从节点组成。其中未编码子任务节点为Iu={1,2,3},Ic={4,5}。若假设主节点收到最快完成计算任务的从节点集合为Su={2},Sc={4,5}，则1 号节点和3 号节点所负责的未编码子任务结果出现了掉队情况，需要通过收到的编码子任务来求解，即求解下列齐次线性方程组，便可求出对应掉队任务结果。

2.5 从节点FHT 计算

前文主要阐述了FHT 的编码分布式并行加速方案，本节围绕FHT 的计算方式，阐述了编码分布式FHT 方案在从节点上的计算任务。

FHT 本身可以通过蝶形运算的形式来表示，图2展示了一个4 维向量通过蝶形运算完成FHT 的过程。总体来看，FHT 的复杂度可以表示为 O(r×2r×N)，其中2r×N表示了待变换矩阵的规模。而经过前文所述的编码环节，每个子矩阵的大小都变为了。因此，从节点上的计算复杂度降为。

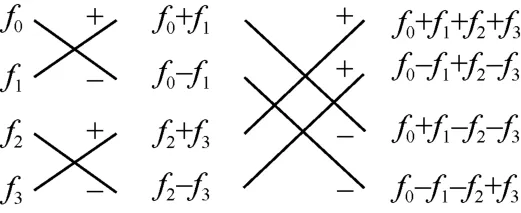
图2 FHT 蝶形运算计算顺序

3 实验验证

本节针对前述系统型MDS 码编码分布式FHT方案进行了实验验证，分析了编码环节、译码环节以及从节点FHT 的复杂度，并在AWS EC2 计算集群上验证了所提方案的有效性。首先，简要介绍了实验环境设置和实验参数设置；其次，针对系统型MDS 码编码分布式FHT 方案的编码环节、译码环节以及从节点FHT 进行了复杂度分析；之后，以目前北斗导航系统中采用的64 元200 码长的多元LDPC 码为基础[19-20]，分析了类似参数的其他多元LDPC 码字的译码加速效果。此外，还与FHT-QSPA进行了译码性能对比，证明了本文方案可以在保证相同的译码精度的情况下，通过分布式并行计算，显著加速FHT-QSPA 译码。

3.1 实验环境设置

为验证本文所提编码分布式FHT 方案的译码加速性能，本节基于AWS EC2 环境搭建了分布式计算集群，并基于MPI 消息传递库开发了编码分布式FHT 方案。测试码字上以北斗系统中使用的64 元(200,100)LDPC 码为基础，并拓展了不同的有限域阶数和不同的码长。有限域阶数包括GF(16)、GF(32)、GF(64)、GF(128)和GF(256)。码长则包括200、400、800、1 600 和2 000。在EC2 实例的选择上，本文选择了t2.micro 类型的实例，其具体配置为1 vCPU 和1 GB 内存。在此基础上，测试了上述码字的FHT 环节和IFHT 环节经系统型MDS 码编码分布式FHT 方案后取得的加速效果。所有的耗时数据均为100个码字完成译码或达到最大迭代次数后单次校验节点更新中各个计算步骤耗时数据的均值。

3.2 复杂度分析

本文所提编码分布式FHT 方案的主要计算步骤包括编码环节和译码环节，以及从节点FHT。编码分布式FHT 方案计算复杂度如表3 所示。

表3 编码分布式FHT 方案计算复杂度

3.2.1 编码环节复杂度对比

在编码分布式FHT 方案的编码环节中，主节点需要对划分好的子矩阵进行随机线性组合，即每个子矩阵先乘以一个随机系数再进行相加。因此，编码环节的复杂度由冗余节点数量和子矩阵大小构成。k表示从节点中执行未编码子任务的节点数量，反映了加速倍数。k越大，则加速倍数越大，对应n-k越小，掉队节点抑制能力也越小，此时编码复杂度越低。因此，本文方案的编码环节复杂度和掉队节点抑制能力存在一个折中。

3.2.2 译码环节复杂度对比

此外，若未编码从节点不掉队，本文方案不需要执行译码；若未编码从节点出现掉队，则译码环节需要求解由ns个方程组成的齐次线性方程组。相应的复杂度主要由未编码子任务中的掉队节点数量ns和子矩阵大小构成。

多项式码编码矩阵乘法方案[11]由于其特殊的幂次多项式编码嵌入结构，使多项式码方案在浮点型数据的译码恢复精度很差。而在FHT 中，多项式码方案随着节点数量增加已不能正确译码。文献[12]和后文恢复误差分析也说明了这一点。但文献[12]所提的正交多项式码编码矩阵乘法的译码复杂度为O(N×2r×k2)，仍然高于本文方案的。

3.2.3 从节点计算环节复杂度对比

另外，从节点上执行的是规模更小的FHT，其复杂度是单节点执行的，并且多个从节点并行执行可以加速FHT。然而，与文献[11]和文献[12]所提出的编码矩阵乘法方案相比，2 种方案将待变换矩阵和FHT 系数矩阵均进行了编码，破坏了FHT系数矩阵的蝶形运算结构，使从节点上FHT 由蝶形运算退化为矩阵乘法，其计算复杂度则由大幅增加为。而本文方案优化了编码冗余嵌入方式，在从节点上维持了FHT 的高效蝶形运算结构，降低了从节点上的计算复杂度。

3.3 数值稳定性

文献[11]中的多项式码编码矩阵乘法方案，由于其编码生成矩阵内生的范德蒙矩阵结构，其矩阵条件数随着从节点数量增加而快速增加，使编码系数矩阵求逆的数值稳定性很差，极大地影响了浮点型数据的译码恢复，文献[12]的实验同样反映了这一点。

针对FHT-QSPA 的FHT 和IFHT，其计算的是多元符号所对应的各个有限域元素的概率值。而这意味着FHT-QSPA 对编码分布式算法造成的译码恢复误差更加敏感，一旦译码恢复数值精度较差，必然会影响后续的译码性能。所以，本文采取的恢复误差计算式为

其中，[Qmn]表示单节点自行完成FHT 的结果，表示采用编码分布式计算得到的FHT 结果。本文对比了所提系统MDS 码的编码分布式FHT方案和文献[11]中提出的多项式码编码矩阵乘法方案以及文献[12]中提出的正交多项式编码矩阵乘法方案的最大恢复误差，统计结果如表4 所示。

表4 3 种方案最大恢复误差

从表4 可以看出，3 种编码分布式方案的数值精度随着从节点数量n的增加都呈现增加的趋势。然而正如前文分析，多项式码方案的数值稳定性随着节点数量增加而急剧恶化，当从节点超过5 个时，其最大恢复误差已经大于0.01，而这样的误差无疑会对FHT-QSPA 的概率更新产生极大影响；而当节点数继续增大时，多项式码方案已不能正确完成译码恢复。对比来看，正交多项式码方案着重改进了多项式码方案的数值稳定性，在20 个从节点的分布式设置中仍旧保持了1×10-13级别的恢复误差。而本文所提的基于系统型MDS 码的编码分布式FHT 方案的最大恢复误差是三者中最小的。

3.4 加速效果

在本文方案中，主要的设计参数有从节点的总数n、未编码从节点的数量k、节点的掉队程度λ和掉队节点数量s。其中，从节点总数n比较容易理解，n越大，分布式并行加速效果越好。而参数k则表示主节点在n个从节点中选择前k个节点作为未编码节点，分配未编码子矩阵；剩下的n-k个节点则作为冗余节点，分配编码子矩阵。因此本文所提编码分布式FHT 方案所能容忍的掉队节点数量等于n-k，而对FHT 和IFHT 的理论加速倍数为k。换言之，本文使用冗余节点换取了分布式方案中对掉队节点的容忍。

此时，节点的掉队程度或计算速度可以由主节点进行监控，当节点计算速度正常或掉队程度较低时，k可以设置得较大，换取较好的加速效果；而当节点繁忙程度增加，节点计算速度下降时，k则可设得较小，使n-k较大，换取较好的掉队抑制效果。

3.4.1 从节点数n对加速效果的影响

首先，分析系统型MDS 码编码分布式并行加速的FHT 和IFHT 在执行耗时上的效果。在码字选择上，统计了码长为200 的64 元LDPC 码在校验节点更新中FHT 和IFHT 的耗时，并在分布式环境下进行了对应的耗时分析，具体结果如图3 所示。

图3 200 码长的64 元LDPC 码编码分布式FHT 和IFHT 耗时

图3 中共有6 组实验结果。第一组数据表示由单节点自行计算FHT 和IFHT 的总耗时，200 码长的64元LDPC 码在单次校验节点更新过程中，FHT 和IFHT总耗时约为191 ms。第二组数据(n=5)中的白色部分表示使用5个从节点对FHT和IFHT进行分布式计算，其耗时总计约42 ms，加速倍数约为4.5 倍；而灰色柱则表示使用编码分布式FHT 方案对FHT 和IFHT 进行加速，其耗时约为49 ms，加速倍数约为3.9 倍。因此，编码分布式FHT 方案通过设置冗余节点，虽造成分布式并行加速倍数稍有降低，但克服了掉队节点的拖累，使分布式FHT 获得了稳定的加速。

3.4.2 掉队程度λ对加速效果的影响

图3 的第二组数据的白色部分表示分布式并行实验，即5 个从节点中未设置掉队节点，此时分布式加速倍数接近于理想加速倍数5 倍。但是当节点出现不同程度的掉队时，其加速性能无疑会劣化。后4 组数据中的白色部分反映了当5 个节点中有1 个节点出现掉队情况时，分布式执行的FHT 和IFHT 总耗时。其中，λ表示节点的掉队程度，即掉队节点的计算速度退化为未掉队节点的。4 组数据中的白色部分反映了当节点掉队程度加深，分布式计算的实际加速效果不断退化，甚至超过未采用分布式计算的耗时(λ=5)。

加入系统型MDS 编码分布式计算后的实验数据绘制如图3 后4 组数据中的灰色部分所示。在编码分布式FHT 方案中冗余节点数量设置为1，因此该方案可以对抗5 个节点中任意1 个节点的掉队，而该方案的理论加速性能为4 倍。与5 个节点纯分布式计算相比，1 个冗余节点的编码分布式FHT 方案相比纯分布式方案理论加速性能略弱，总耗时约为50 ms。但是随着节点掉队程度的加深，编码分布式FHT 方案的加速性能不受掉队节点的影响，稳定在50 ms 左右。因此，编码分布式FHT 方案能够通过冗余节点设计抵抗掉队节点的影响，且节点掉队程度加深对整体加速性能没有劣化。

3.4.3 掉队节点数量s对加速效果的影响

由于编码分布式FHT 方案中通过设置冗余节点来克服节点掉队，而图3 反映了节点掉队程度的加深对并行算法的加速效果有很大的影响。因此，图4 对掉队节点数量进行了实验，其中从节点数量为n=10，冗余节点数量为n-k=5，节点掉队程度为λ=2，码字参数与图3 实验一致。编码分布式FHT 方案可以在冗余节点数量范围内容忍不同数量的掉队节点，而不增加FHT 和IFHT 耗时，即基于系统型(n,k)MDS码的编码分布式FHT 方案能够抵抗任意小于或等于n-k个节点掉队。当节点掉队数量超过了冗余节点数量时，此时整个分布式系统中的掉队情况更加严重。例如，当10 个从节点中有6 个节点掉队时，主节点在收到4 个从节点结果的基础上至多还需要等待任意1 个从节点的计算结果便可完成译码恢复。因此，当掉队节点数量超过冗余节点数量时，主节点可以在下一次迭代更新中进一步增大冗余节点数量，以实现更好的抗节点掉队效果；反之，当节点掉队数量小于冗余节点数量时，主节点也可在下一次迭代更新中降低冗余节点数量，达到更好的并行加速效果。

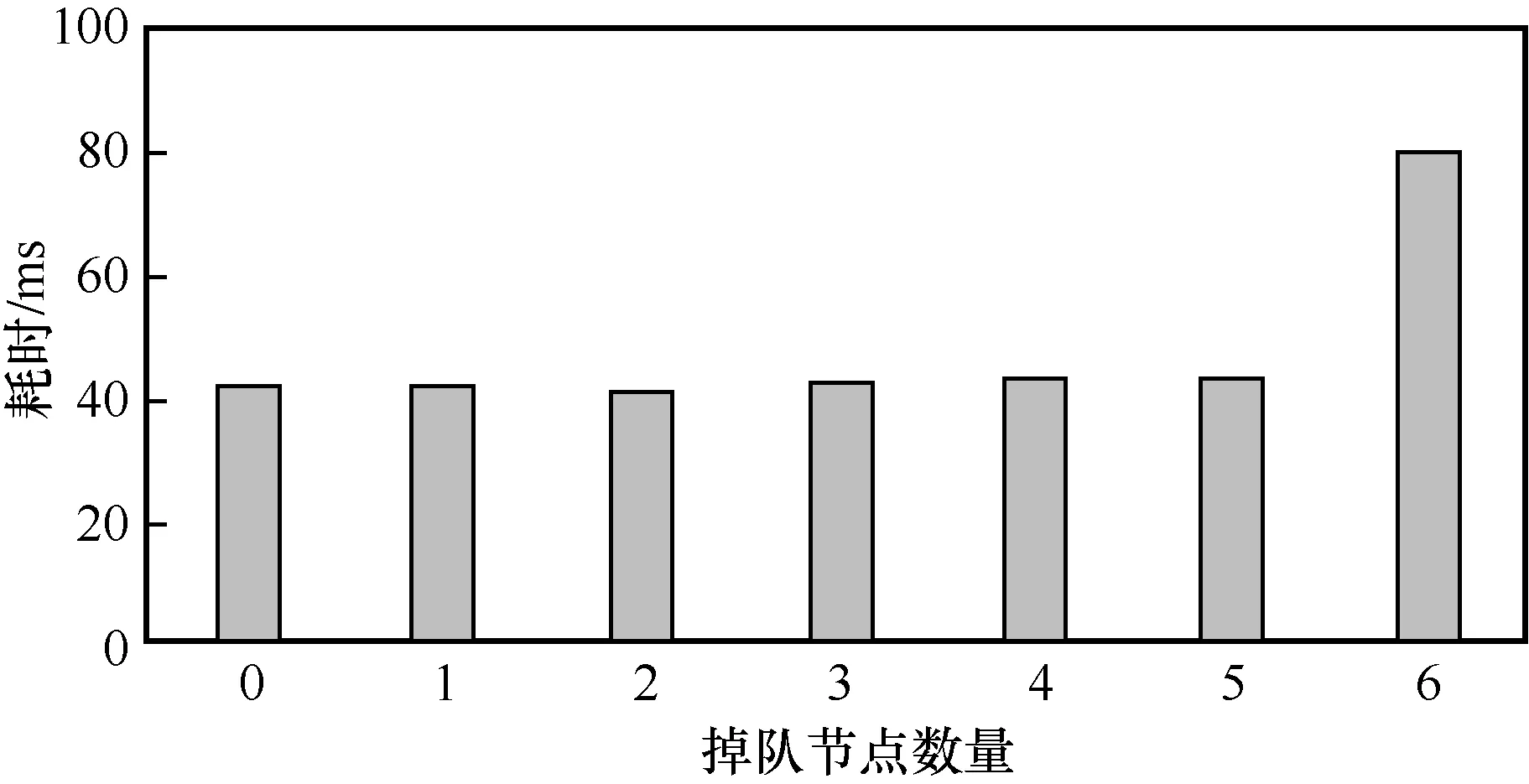
图4 不同掉队节点数量s 对编码FHT 和IFHT 的耗时影响

3.5 不同参数NB-LDPC 码加速效果

根据前文分析，编码分布式FHT 加速方案不受节点掉队程度影响，实现了稳定加速。因此，本文继续使用5 个从节点，其中有1 个冗余节点的编码分布式参数设定，分析不同码长和不同有限域阶数上的加速效果。选择掉队节点数量为1 个，节点掉队程度λ为2。在不同码长的64 元LDPC 码上，编码分布式方案对FHT和IFHT加速效果如图5所示。当码长从200 增长到2 000，FHT+IFHT 的总耗时从191 ms 快速增加到了2 105 ms。而编码分布式FHT+IFHT 方案能够稳定地并行加速FHT 和IFHT，提升两者计算效率。

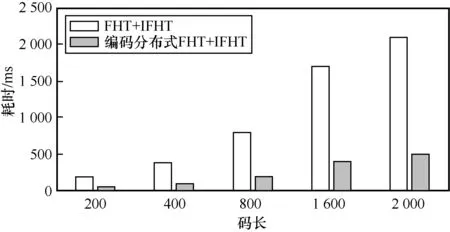
图5 不同码长的64 元LDPC 码FHT 和IFHT 耗时

接下来，固定码长为200，将有限域阶数从16增加到256 时，对应的编码分布式FHT 加速方案效果如图6 所示。随着有限域阶数的增加，FHT+IFHT的总耗时从49 ms 增长到866 ms。因此，如图5 和图6 中灰色数据所示，特别是针对码长变长和有限域变大的情况，编码分布式FHT 方案大幅节约了FHT 和IFHT 计算时间，加速了校验节点更新，从而加速了整体FHT-QSPA 译码过程。

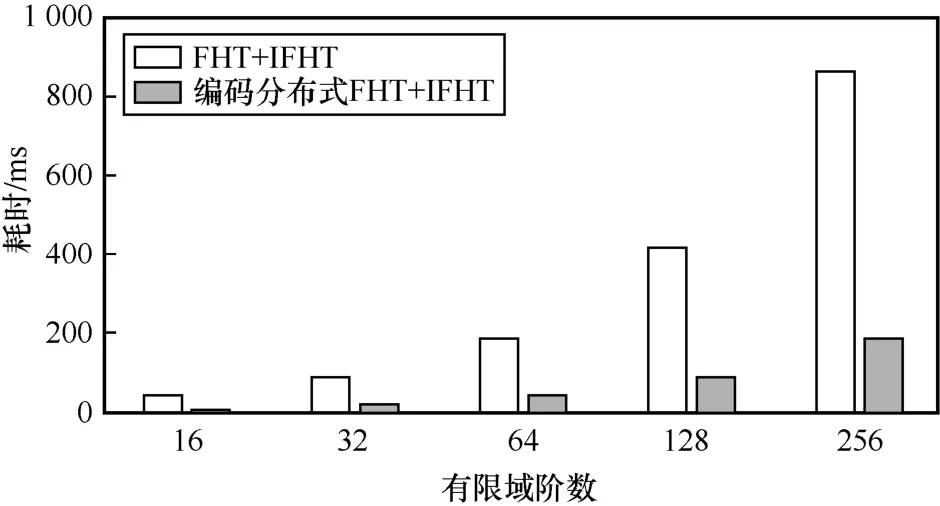
图6 200 码长的不同有限域阶数LDPC 码FHT 和IFHT 耗时

3.6 译码性能对比

本节选用了码长为800 的16 元LDPC 码作为测试码字。首先通过随机方法得到了码字生成矩阵，之后对随机生成的信息进行编码，并进行BPSK调制，其后经过AWGN 信道加噪，最后分别使用FHT-QSPA 和基于编码分布式方案的FHT-QSPA 进行译码，分析其译码性能。图7 给出了2 种算法的译码性能曲线。从图7 可以看出，基于编码分布式FHT 方案的译码算法的译码性能相较于原始算法没有损失。

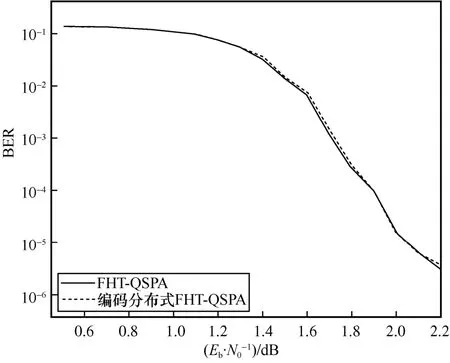
图7 FHT-QSPA 和编码FHT-QSPA 的译码性能曲线

除此之外，本文还进一步分析了FHT-QSPA 和编码分布式FHT-QSPA在单次校验节点迭代中FHT和IFHT 的耗时情况，如表5 所示。其中编码分布式FHT 采用了5 个从节点，其中有1 个冗余节点的分布式设置，而掉队节点数量设置为1 个。从表5 可以看出，通过编码分布式的改造，使FHT 和IFHT 这2 个耗时最长环节得到了稳定加速。

表5 2 种译码算法单次迭代耗时

4 结束语

本文提出了一种基于系统型MDS 码的编码分布式FHT 方案。该方案在主节点上将信道概率建模为矩阵并对其进行切分，再编码生成冗余子矩阵；其后，主节点将所有子矩阵卸载到从节点并行执行FHT 和IFHT，然后从节点将计算结果传回主节点完成最终译码。通过设置不同的冗余节点数量，该方案可以在加速性能和抗节点掉队性能之间取得折中。此外，本文证明了所提系统型MDS 码编码计算方案能够以概率1 的可能完成掉队任务结果的译码恢复，而译码过程仅需对齐次线性方程组进行求解。

总体来看，本文方案的编译码环节的复杂度均较低，这使编码分布式FHT 加速方案针对FHT 和IFHT 均获得了接近于k倍的加速。将本文方案的译码恢复误差与其他编码矩阵乘法方案进行对比，验证了本文方案优秀的数值稳定性。而不同有限域和码长的多元LDPC 码译码耗时分析，确认了本文方案的加速效果。译码性能曲线对比表明了本文方案可以在不损失译码性能的情况下，稳定地加速译码过程。

另外，本文方案还适于其他变换，例如FFT 等。通过对待变换矩阵进行编码分布式加速，可以同时实现较高的抗节点掉队性能和保持高效变换计算结构。后续本文将继续研究该方案在其他变换上的应用，拓展系统型MDS 码编码分布式加速方案的应用场景，提高计算效率。